初中数学解题思路探析
江西省宜春市澡溪学校 胡 娟
初中数学解题思路探析
江西省宜春市澡溪学校 胡 娟
初中数学是一门重要的学科,其涵盖了三角函数、代数以及几何等多方面内容。而这些基础知识不但能够将学生的数学学习情况反映出来,而且还会对其今后更深层次知识的学习产生一定影响。所以,初中数学教师应当结合学生实际学习情况,根据理论基础知识去建立起有效的初中数学解决思路,让学生能够更轻松地学习初中数学知识,从而促进初中数学教学质量的有效提升。为此,下文就初中数学解题思路进行简要分析。
一、对称性解题思路
对称性解题思路指的是根据对称原理,运用形象或抽象思维来构建起具有对称特征的几何图形、数学模型以及代数表达式。如“等腰三角形的两个底角相等”、“圆的直径能够平分圆”等,并且在初中数学题目中也存在着许多类型的对称,如对称方程式、对称不等式、中心对称图形、轴对称图形等,部分数学题目中还隐含着对称的条件,所以在解决和对称相关的数学题时,可以有效应用对称性解题思路来进行解题,以简化解题步骤,提高解题效率。
例1 已知0<a<1,0<b<1,0<c<1,求证abc(1-a)(1-b)(1-c)≤( )3。

证明:∵题目已知0<a<1,

二、数形结合解题思路
数形结合是初中数学最为常用的解题思路之一,尤其是在进行函数解题时,我们不难发现函数变量与图形间是一个相辅相成的关系,在函数变量中隐含有图像资料,而图像又能够将函数的变量关系反映出来。所以在解答初中数学函数题目时可以结合图形来进行,通过直观的图形去正确掌握其存在的函数关系,从而使得函数解题更为简便。
例2 已知一次函数y=ax+b的图像如图1所示,具体求解问题如下:
(1)分别计算出系数a与b的值;
(2)将函数y=bx+a的图像在直角坐标系中画出,
并对两个图象间的函数关系进行观察。
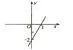
图1
解题思路:根据题目中给出的已知信息,并采用数形结合的解题思路可以发现:直接将直线和x轴与y轴的交点(1,0),(0,-2)代到函数关系式y=ax+b中就能够将a,b的值计算出来,如此一来不仅大大简化了解题程度与难度,而且还有利于提高学生的解题效率。具体解答如下:
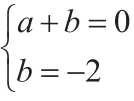
(2):将所求得的a=2,b=-2的值代入到函数y=bx+a中可得出y=-2x+2的关系式,画出图像,如图2所示:
将函数y=ax+b的图像与函数y=ax+b的图像进行比较,可以从中发现一个规律,就是这两个图像关于x轴对称。

图2
三、化归解题思路
化归指的是在解题过程中,把一种数学对象在一定条件下转化为另一种数学对象的方法,简单来说,即将复杂、陌生的问题转变为熟知、简单的基本解题模式。在初中数学解题过程中,化归解题思路有着极为重要的作用。
例3 已知a2+a-1=0,求a3+2a2+2009的值。
解题思路:该数学问题看来结构比较复杂,如果采用常规的方法来逐一进行乘方计算,不但过程繁杂,而且容易出错。所以在解该道题目时,可由结构着手,转化其结构,从而快速将其解答出来。
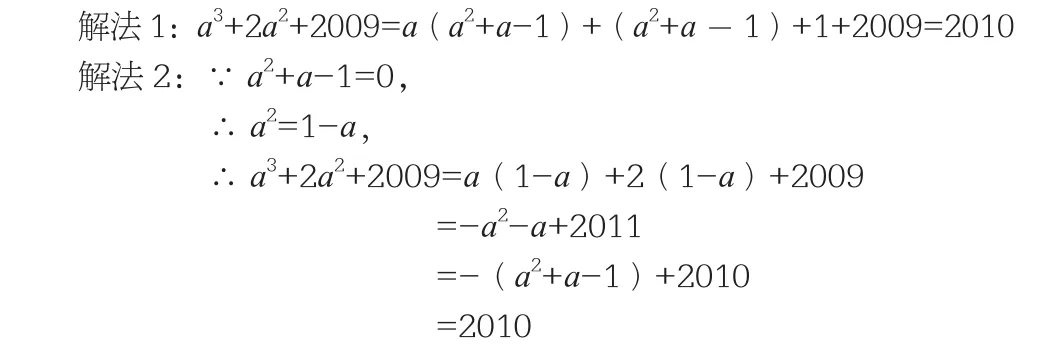
例4 如图3所示,梯形ABCD中,AB=CD,BC∥AD,BD、AC两条对角线相较于O点,且AC⊥BD,BC=5,AD=3,求AC长为多少。
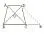
图3
解题思路:在求解过程中,可以将未知条件化归为已知或容易解决的问题,从而便能有效进行解答。该道题目是利用了梯形对角线互相垂直的特点,将对角线进行平移,便可把等腰梯形转化为平行四边形与直角三角形,从而解出答案。
解:从D点做延长线与AC平行,延长至E点,得到CE=AD,DE=AC,而BE=BC+CE,则可将CE=AD带入式子中,得出BE=8。

在等腰直角三角形BDE中,BE2=BD2+DE2