基于稳定图和矩阵束算法在风机系统低频振荡参数辨识的应用

,

(1.新疆大学电气工程学院，新疆 乌鲁木齐 830047；2.国网新疆电力公司，新疆 乌鲁木齐 830002)



基于稳定图和矩阵束算法在风机系统低频振荡参数辨识的应用

苗长越1，姚秀萍1,2，王海云1，朱建华2，常喜强2，李自明1，李朝阳1,贺成龙2

(1.新疆大学电气工程学院，新疆 乌鲁木齐 830047；2.国网新疆电力公司，新疆 乌鲁木齐 830002)

为了精确检测含有风机的电力系统低频振荡参数，提出了一种稳定图和矩阵束相结合的新算法。首先用稳定图法确定区间低频振荡信号的阶数,在得到了系统阶数之后，就可以应用矩阵束算法得到每个分量的幅值和特征根，进而可以获得系统的阻尼比、幅值和频率。最后的仿真实验结果表明，与TLS-ESPRIT算法相比，该方法计算的阻尼比最大相对误差更小。在不同的系统中，运用该方法依然可以得到较准确的结果。

风力发电机；低频振荡；矩阵束算法；稳定图法

0 引 言

随着单机系统的容量日益增加，电力系统的规模也日益增大，对系统的稳定性提出了新的要求。自从互联大电网系统诞生以来，低频振荡的问题一直也伴随产生，所以低频振荡参数辨识的研究一直以来都受到国内外学者的重视，随机子空间、HHT、Prony、矩阵束等方法都在电力系统低频振荡参数辨识中得到了充分应用[1-5]。

此外，伴随着能源危机的不断加深，探索新型的能源发展之路对中国的能源供应显得尤为重要。风能作为较为成熟的新能源，得到国家的大力支持。随着风机接入容量的不断增加，对系统稳定的影响也显得较为明显。因此研究含风机系统的低频振荡问题就具有一定的实际意义[6-7]。矩阵束算法作为一种较为有效的参数辨识方法，不仅单独使用时具有一定的辨识精度[5]，而且与其他的方法具有良好的配合性[8-11]。文献[9]结合了矩阵束算法和小波用于同步电机的参数辨识，结论表明两者结合可以取得较高的辨识精度。文献[10]改进了矩阵束算法，并将其用于次同步震荡的参数辨识，取得了较好的辨识效果。上述的结论从一定程度上表明，矩阵束算法不仅具有优良的参数辨识效果，而且可以与其他的算法结合，具有较好的理论融合度。

下面首先使用稳定图法定阶，对含有噪声的信号去噪，提高信号的信噪比。然后对去除噪声之后的信号进行矩阵束算法处理，得到辨识信号的幅值、阻尼、频率等参数。最后是仿真测试，分别对模拟信号、单机无穷大系统的信号和多机系统的信号进行参数辨识，辨识结果说明了所提方法的有效性。

1 稳定图法

在低频振荡的参数辨识问题中，首先需要进行的是模型定阶，然后才能辨识其他的参数。稳定图方法[11]是一种较为严格的模型定阶的方法。

稳定图法主要的原理为：首先假设系统不固定，先假定系统具有一个较大的阶次，依次递减，可得到相应于不同阶次的系统参数。通过矩阵束法对每个阶次的模型进行参数辨识，并将模态参数绘制到二维坐标图上，可得到多组阶数图。稳定图的自变量为频率，因变量为系统阶次。通过比较两个相邻阶次的参数，如相邻阶次的差值保持在预先可以接受的范围内，就此认定该模态为稳定的。由于扩大了阶次的搜索范围，所以虚假模态的出现几乎是不可避免的。伴随着阶次的累加，对应于稳定的模态，极点几乎会形成一条很少偏斜的直线，被称为稳定轴，而虚假模态的极点往往会出现偏斜。假定特征频率的容差为εf，要形成稳定轴需满足：

(1)

式中：j为模型阶次；f为各阶次下估计的模态频率。

稳定图有助于得到正确的信号阶数，因而具有一定的理论价值和实用价值。

2 矩阵束算法

带有噪声的均匀采样信号y(k)可表示为

(2)

式中：Ai为第i个分量的幅值，可以为复数或实数；Th为采样信号的周期；k为采样点数；w(k)为噪声。对采样信号y=[y(0),y(1),L,y(k-1)]T构造Hankel矩阵Y(k-l)×(L+1)，L的一般取值范围在k/4～k/3之间[6]。

然后对Y进行SVD分解，可得Y=U∑VH。实际中较为关心的是∑中前面较大的特征值。取前q个较大的特征值Zi所在的列构成∑1及Zi对应的右特征向量vi构成V′=[v1,v2,L,vq]。v1和v2分别表示删去矩阵V′的第一行和最后一行，记Y1=U∑1V2H，Y2=U∑1V1H。可以证明：矩阵束﹛Y1Y2﹜的广义特征值Zi与特征根si之间的关系为

(3)

因而只要求解以下广义特征值，即可得到待辨识信号y(k)的幅值和特征根。

Y1u=zY2u

(4)

Ai则可由式(5)的线性方程组通过最小二乘法求解得到。

(5)

A=(ZHZ)-1ZHy

(6)

3 仿 真

3.1 设计步骤

首先应用稳定图法对信号进行定阶分析，得到系统的阶数之后，识别出其中的信号分量；其次利用矩阵束算法辨识出低频振荡信号的幅值、阻尼和频率等参数值；通过3组仿真信号的验证，证明所提方法的有效性。

3.2 模拟信号分析

将低频振荡信号视为某些频率固定、幅值按指数规律变化的正弦信号(振荡模式)的线性组合，则含随机噪声的振荡模式可表示为

y(k)=e-0.2tcos(2πf1t)+e-0.5tsin(2πf2t)+w(t)

(7)

式中：f1=1.5 Hz；f2=1.0 Hz。仿真采用的信号为数字信号，采用频率为200 Hz，噪声的方差为0.04。

为了研究所提方法的效果，特地引入噪声，见图1。然后做了对应的仿真分析，使得分析的结果能够更加有说服力。采用的对照方法为总体最小二乘旋转不变技术(total least squares-estimation of signal parameters via rotational invariance technique，TLS-ESPRIT)。

显然，可直接用总体最小二乘旋转不变技术识别得到振荡频率和阻尼系数，辨识结果见表1的前3行。由表1可知：采用矩阵束得到的阻尼比的最大相对误差为1.2%；采用总体最小二乘旋转不变技术识别得到的阻尼比的最大相对误差为2%。

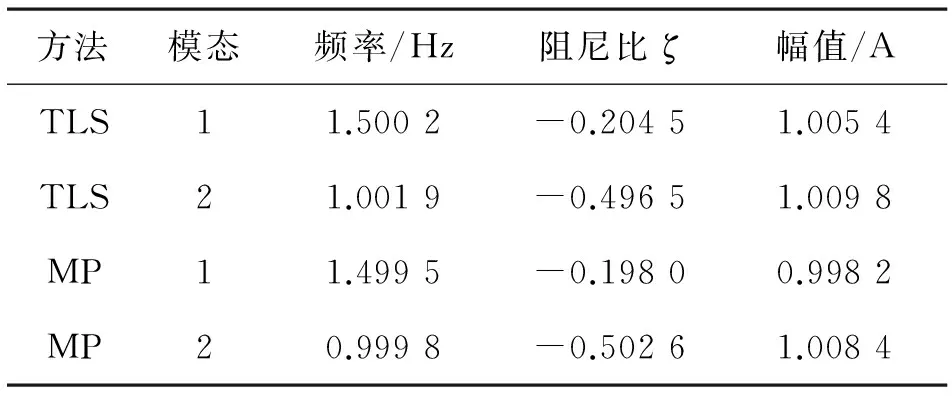
表1 含噪信号的低频振荡模态分量参数

表1是在SNR=27.9 dB的情况下的仿真结果，其中第5列的所提算法是未加入小波滤波时的参数误差。由表1不难发现，在信噪比达到27.9 dB时，所提方法总体的辨识效果要略优于对照的方法。

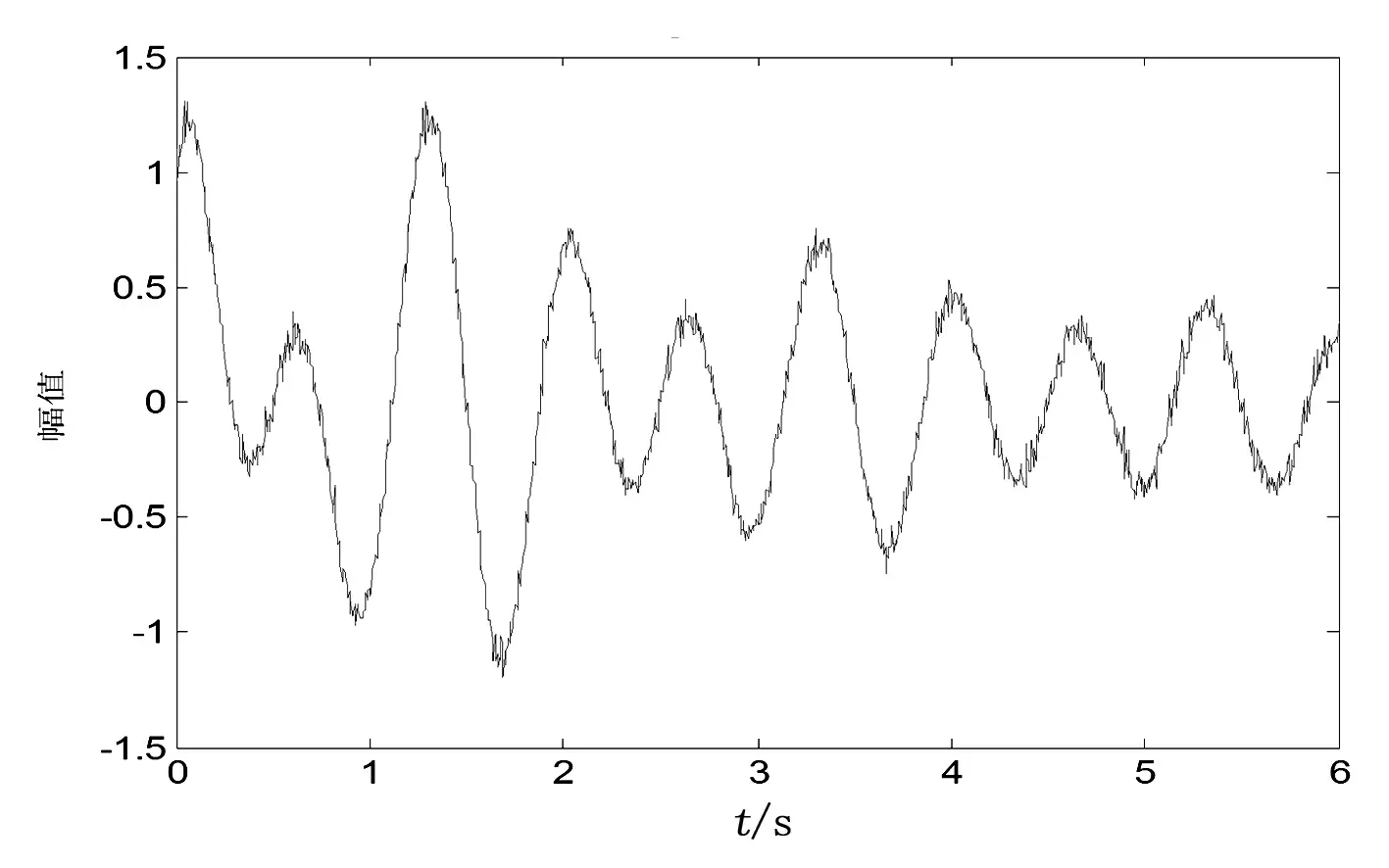
图1 含噪信号的仿真图

3.3 单机系统分析

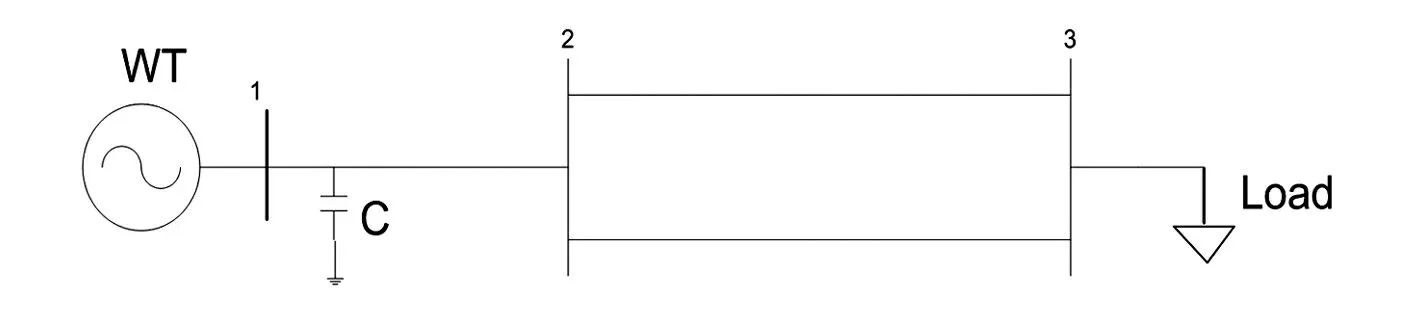
图2 单机无穷大系统示意图

风机的容量为275 kV·A，电压为480 V，负荷在0.2 s发生突变，由50 kW增加到75 kW。异步风机的主要参数为：定子电阻Rs=0.016；定子电感L1s=0.06；转子电阻Rr=0.015；转子电感L1r=0.06；励磁电感Lm=3.5；惯性时间常数H=2 s；阻尼系数F=0；极对数p=2；电容的容量为75 kvar；风速为10 m/s。

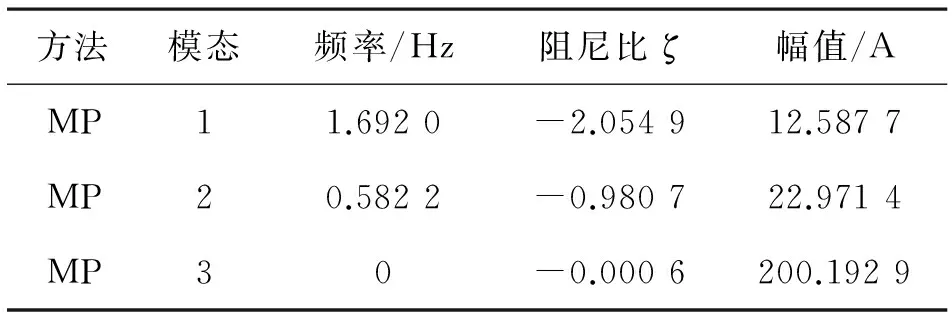
表2 单机系统挠动下的低频振荡模态分量参数

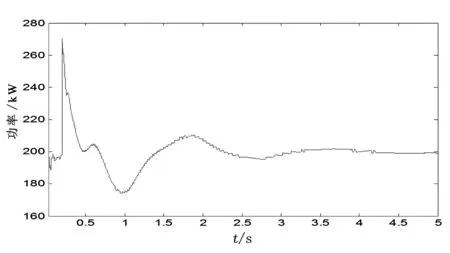
图3 单机系统扰动下的系统振荡功率图

单机系统小扰动下系统参数如表2所示，有两个振荡分量和一个直流分量。直流分量为系统的稳态运行功率，振荡分量主要是由负荷阶跃变化产生的，单机系统扰动下的系统振荡功率如图3所示。稳定图(图4)显示的结果也表明了系统的振荡分量和直流分量。

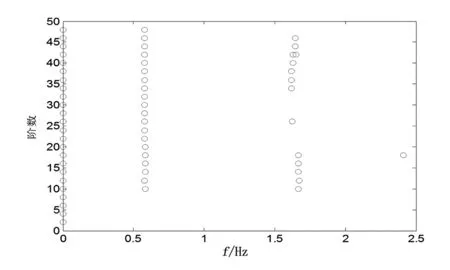
图4 振荡功率的稳定图

3.4 IEEE 5机14节点系统分析

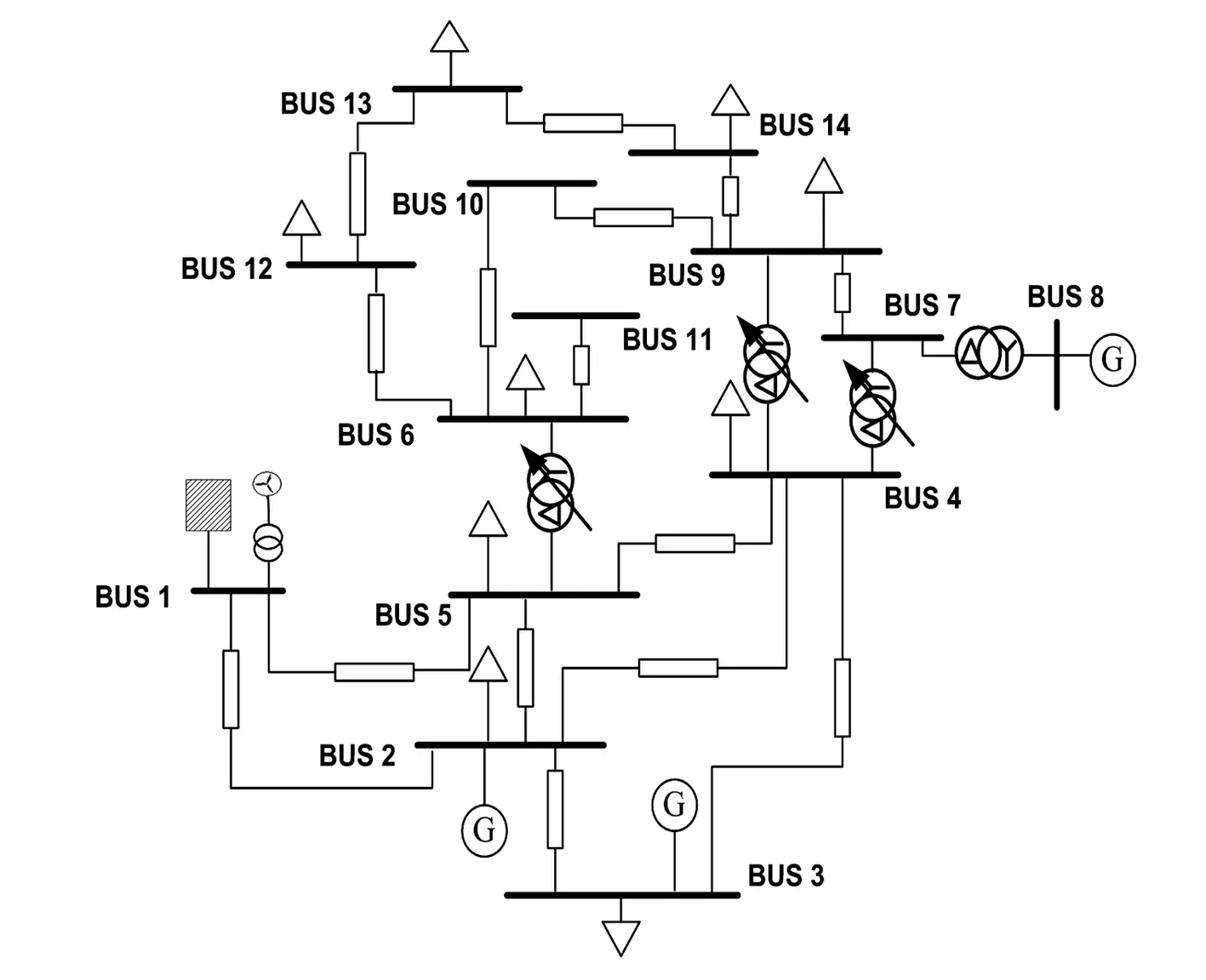
图5 IEEE 5机14节点系统示意图

IEEE 5机14节点示意图如图5所示，在母线1处接入双馈风机，风机的容量为600 MV·A，负荷在1 s发生突变，双馈风机的主要参数为：定子电阻Rs=0.01，定子电抗Xs=0.01，转子电阻Rr=0.01，转子电感Xr=0.08，励磁电感Xm=3，惯性时间常数H=6 kWs/kV·A。

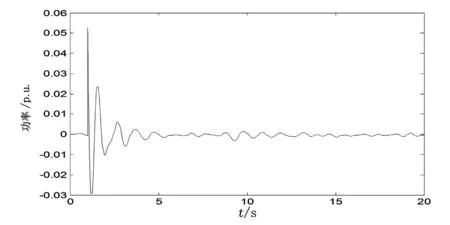
图6 IEEE 5机14节点系统功率振荡示意图

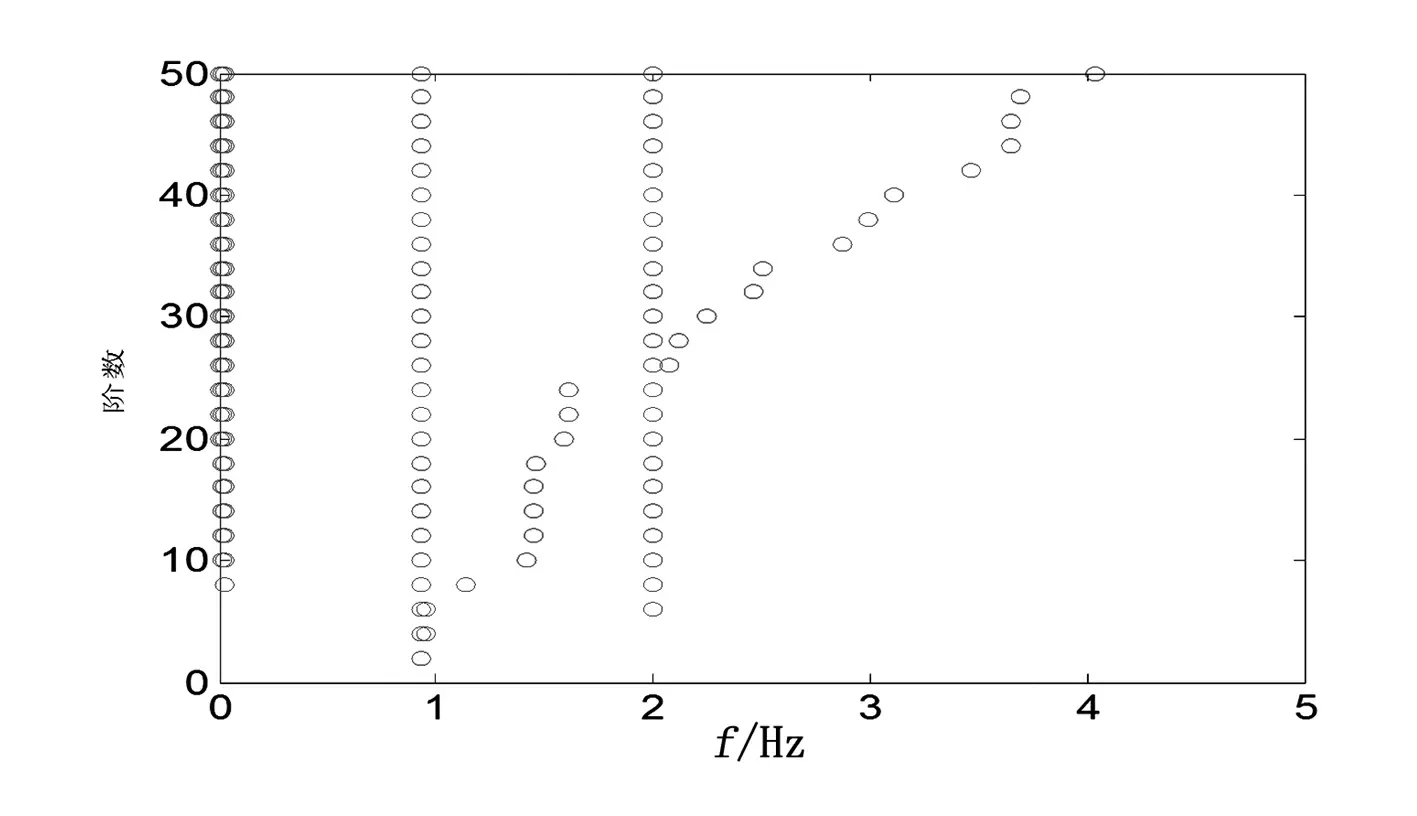
图7 传输功率的稳定图

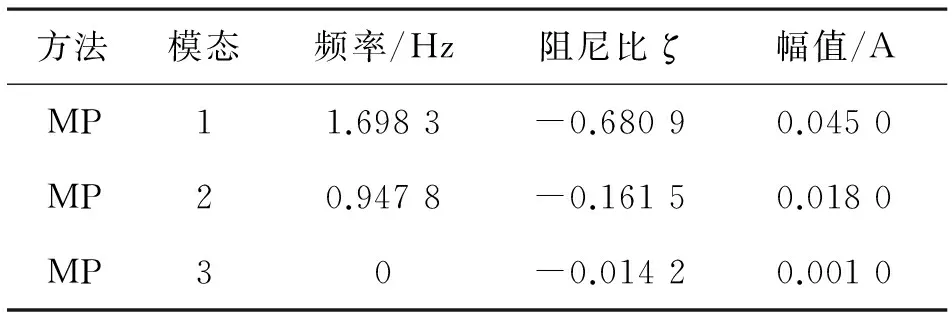
表3 IEEE 5机14节点系统的低频振荡模态分量参数

IEEE 5机14节点系统大扰动下系统参数如表3所示，有两个振荡分量和一个直流分量。振荡分量主要是由线路短路产生的。稳定图(图6、图7)显示的结果也表明了系统的振荡分量和直流分量。

4 结 论

将矩阵束算法应用于含有风机的电力系统低频振荡参数辨识问题，该方法的优点是可以无需多次迭代，而且能在计算量能够接受的情况下得到较高的辨识精度。

1)所提算法既可以处理非线性平稳信号，也可以处理非线性非平稳信号，取得很好的效果。

2)在系统正常运行或者小扰动下可直接用稳定图法辨识阶数，然后用矩阵束算法识别系统的弱阻尼模式和模态参数，为PSS的安装提供参考依据。

此外，矩阵束算法运算速度快，辨识精度高，结合稳定图的广泛应用，为含有风力发电机的电力系统低频振荡的在线分析提供了一种可供借鉴的方法。

[1] 王辉, 苏小林. Prony算法的若干改进及其在低频振荡监测中的应用[J].电力系统保护与控制, 2011, 39(12):140-145．

[2] 李天云, 袁明哲, 李军强，等. 基于EMD和SSI的电力系统低频振荡模态参数识别方法[J].电力系统保护与控制, 2011, 39(8):6-10．

[3] 李天云, 高磊, 赵妍. 基于HHT的电力系统低频振荡分析[J].中国电机工程学报, 2006, 26(14):24-30.

[4] 张静, 徐政, 王峰，等. TLS-ESPRIT算法在低频振荡分析中的应用[J].电力系统自动化, 2007, 31(20):84-88.

[5] 王宇静, 于继来. 电力系统振荡模态的矩阵束辨识法[J].中国电机工程学报, 2007, 27(19):12-17.

[6] 李媛媛, 邱跃丰, 马世英，等. 风电机组接入对系统小干扰稳定性的影响研究[J].电网技术, 2012, 36(8):50-56.

[7] 杨悦, 李国庆, 李江，等. 双馈风电机组电力系统低频振荡阻尼特性[J].沈阳工业大学学报, 2013, 36(1):1-6.

[8] 朱瑞可, 李兴源, 赵睿，等. 矩阵束算法在同步电机参数辨识中的应用[J].电力系统自动化, 2012, 36(6):52-55.

[9] 张宇辉, 陈峰, 李慧敏，等. 基于小波变换和矩阵束算法的同步电机参数辨识[J].电力系统保护与控制, 2012, 40(9):87-92.

[10] 李宽, 李兴源, 赵睿. 基于改进矩阵束的高压直流次同步振荡检测[J].电网技术, 2012, 36(4):42-46.

[11] 常军, 张启伟, 孙利民. 稳定图方法在随机子空间识别模态参数中的应用[J].工程力学, 2007, 24(2):39-44.

[12] 张亮, 张新燕, 王维庆. 基于改进多信号矩阵束算法的电力系统低频振荡识别[J].电力系统保护与控制, 2013, 41(13):26-30.

[13] 陈刚, 吴小陈, 柳勇军, 等. 基于频域分解法和广域稳态量测的低频振荡模式辨识[J].电力系统保护与控制, 2011, 39(12):56-60.

[14] Trudnowski D J. Making Prony Analysis More Accurate Using Multiple Signals[J].IEEE Transactions on Power Systems, 1999, 14(1):226-231.

[15] Hauer J F. Application of Prony Analysis to the Determination of Modal Content and Equivalent Models for Measured Power System Response[J].IEEE Transactions on Power Systems, 1991, 6(3): 1062-1068.

[16] Rouquette S, Najim M. Estimation of Frequencies and Damping Factors by Two-dimensional ESPRIT Type Methods[J].IEEE Transactions on Signal Processing, 2001, 49(1): 237-245.

In order to accurately detect the low-frequency oscillation parameters of power system with wind turbines, a new algorithm is proposed which combines the stabilization diagram and the matrix pencil. Firstly, the order of the interval low-frequency oscillation signal is determined by the stabilization diagram method. After getting the system order, the amplitude and the characteristic root of each component can be obtained by using the matrix pencil algorithm, and the damping ratio, amplitude and frequency of the system can be obtained too. Finally, the simulation results show that compared with the TLS-ESPRIT algorithm, the damping calculated by the proposed method is less than the maximum relative error. In different systems, the proposed method can be used to get more accurate results.

wind turbine generator; low-frequency oscillation; matrix pencil algorithm; stabilization diagram

教育部创新团队(IRT1285)；国家自然科学基金(51267017)；国家863计划(2013AA50604)

TM712 <文献标志码：a class="emphasis_bold"> 文献标志码：A 文章编号：1003-6954(2016)06-0014-04文献标志码：a

1003-6954(2016)06-0014-04

A 文章编号：1003-6954(2016)06-0014-04

2016-09-09)

苗长越(1991)，硕士研究生，研究方向为可再生能源发电与并网技术；

姚秀萍(1961)，教授级高工、硕士生导师，研究方向为电力系统稳定与控制、调度自动化；

王海云(1973)，教授、硕士生导师，研究方向为可再生能源发电与并网技术。