从单摆看空间的升降维现象
方 乐 葛铭纬 柳阳威
(1北京航空航天大学中法工程师学院, 北京 100191;2华北电力大学可再生能源学院, 北京 102206;3北京航空航天大学能源与动力工程学院,北京 100191)
从单摆看空间的升降维现象
方 乐1葛铭纬2柳阳威3
(1北京航空航天大学中法工程师学院, 北京 100191;2华北电力大学可再生能源学院, 北京 102206;3北京航空航天大学能源与动力工程学院,北京 100191)
为了帮助本科生更好地理解现代物理,特别是空间的一些升降维现象,我们从单摆出发,设计了一个启发性的例子,形象直观地对此进行了类比描述.可以看到,若摆臂为刚性绳,则相图中会出现空洞,轨迹触碰到空洞边沿时触发斜抛运动而引起升维现象.这个例子可以类比现代物理中的科学研究,也反映了数学与物理学的紧密联系,适合于工科学生的本科教学.
单摆;空间维数;现代物理
现代物理中的一些深奥的理论,如广义相对论、弦论和M理论,以及通过它们推导出的一些有趣的结论,往往是学生和科幻小说关注的对象.高维空间及其升降维现象[1],以及虫洞现象[2],都是这一类有趣的结论,但对于本科生却并不容易直观理解.本文并不试图从它们的原始定义出发进行阐述,而是以单摆问题作为一个启发性的例子,从对单摆问题的讨论出发,向相关的本科生形象类比地解释这些现代物理中深奥而有趣的结论.

图1 单摆示意图
本文讨论的单摆模型如图1所示,其中摆
长为l,偏转角为θ,重力大小为mg.忽略所有的阻尼并认为机械能守恒.另外,考虑单摆处于惯性系中,从而避免讨论傅科摆的问题.众所周知,当偏转角θ很小时,单摆近似地可以认为是做简谐振动;当偏转角θ较大时,问题则比较复杂.下面我们对此问题进行简单的叙述.
单摆问题可以由如下的方程描述
(1)


(2)
其中,τ=t/t0;X(τ)=(Θ(τ),Θ′(τ))T;Θ(τ)=θ(t),F(X(τ))=(Θ′(τ),-sinΘ(τ))T.因此,该问题可以在(Θ,Θ′)相空间进行描述.在此相空间我们可以很容易地得到其轨迹的相图,如图2所示.可以看到,对k∈Z,(2kπ,0)是稳定的平衡点,而((2k-1)π,0)是不稳定的鞍点.在A点附近的轨线表示单摆的往复振动,而B点附近的轨线表示单摆的单向旋转运动.

图2 单摆在(Θ,Θ′)相空间的轨迹相图

图3 摆臂是刚性绳时,单摆在(Θ,Θ′)相空间的轨迹相图
上面的内容均是传统的单摆理论,在不少分析力学或微分方程定性理论的教科书中都有涉及.事实上,这些分析中隐含了一个重要的假设,即摆臂不发生形变,摆到中心的距离r始终等于l,也即意味着摆臂是无质量的刚体.但如果摆臂不是刚体而是无质量的刚性绳(即只能受拉力且不能被拉长,可认为对应于一种极端的弹性绳情形[3]),上面的分析就不再成立了.在此情形下,我们必须分析刚性绳的受力,一旦刚性绳受压力作用(即cosΘ+Θ′2<0),则r就会发生改变.这时我们画出相应的轨迹相图,如图3所示.注意C点附近的轨线在cosΘ+Θ′2≥0区域的边界停止了,在此之后r减小而摆球发生了坠落.坠落的过程可以用斜抛运动来描述,因此也可以写出相应的控制方程,但其在极坐标下的表示比较复杂,相应的讨论也超出了本文的范围,因此本文不再赘述.
若系统机械能不守恒而是含有阻尼,也可得到类似的结论.比如我们考虑传统的线性阻尼摆,可以得到如下的控制方程
(3)
其中,c是线性阻尼;m是摆球质量.相应的无量纲形式为
(4)

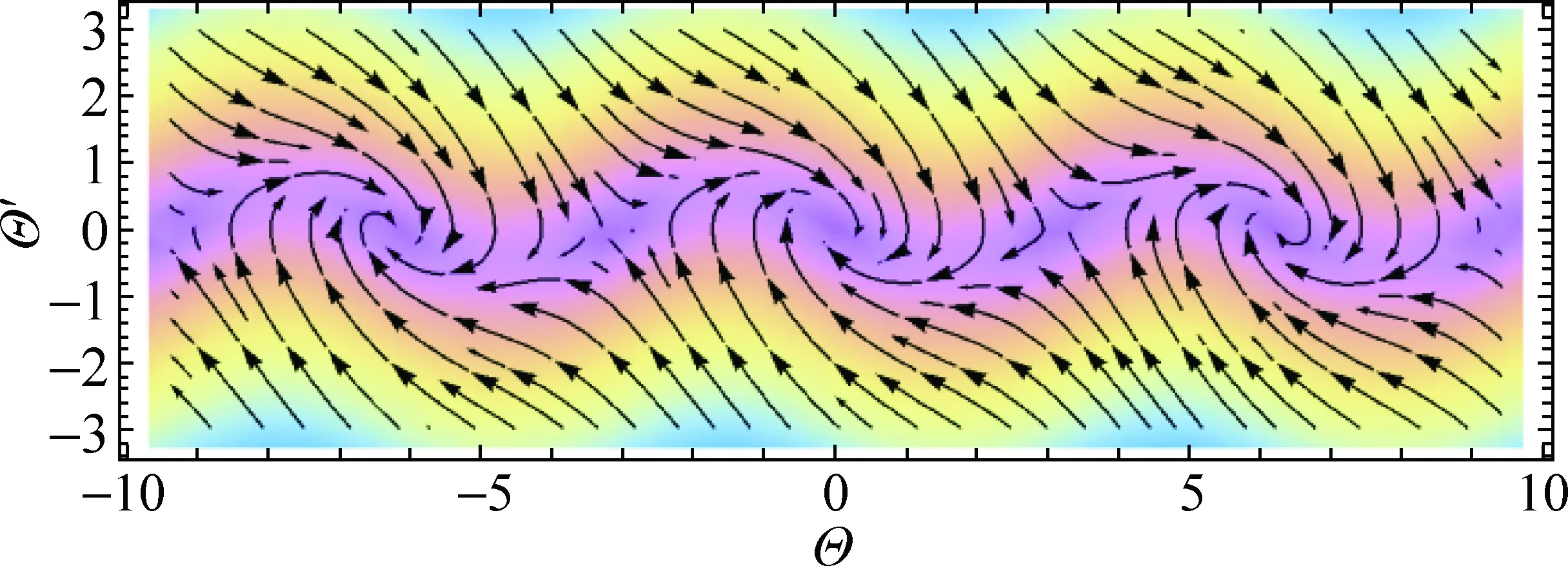
图4 有阻尼单摆在(Θ,Θ′)相空间的轨迹相图

图5 摆臂是刚性绳时,有阻尼单摆在(Θ,Θ′)相 空间的轨迹相图
下面我们大胆地想象一个故事.在小角度摆动的摆球上(对应于图3中A点附近的轨线)生活着一些生命,他们随着摆球一起在一段圆弧上运动,在物理空间我们可以因此说他们生活在一个一维空间之中.但在相空间,他们的运动有两个自由度Θ和Θ′,因此在相空间看这是一个二维空间.在这些生命中有一位“物理学家”观察到了他们的运动,进而总结出了普适的运动方程(1)或(2).进一步,该“物理学家”指出,按照运动方程的预言,如果不断地给他们的世界增加机械能,就能改变其运动轨线,最终达到单向旋转运动(对应于图3中B点附近的轨线).其他的生命都对这个预言非常有兴趣,他们因此通过某些方法增加单摆的机械能,让单摆越晃越高.但不幸的是,他们并不知道摆臂其实并不是刚体,而是刚性绳.在他们试图从A点附近的轨线向B点附近的轨线改变的过程中,他们的世界到达了C点附近的轨线,进而触碰了cosΘ+Θ′2≥0区域的边界.刚性绳不能支持摆球,因而摆球发生了斜抛运动,摆到中心的距离r发生了变化.这时,新的自由度(如r和r′)产生了,他们的世界变成了一个高维世界(在相空间,由二维变为4维;在物理空间,由一维变为二维)!最终摆球重新坠落到了r=l圆弧上,这些新的自由度也消失了.世界又回到了小角度摆动的状态(对应于图3中A点附近的轨线).
尽管这个故事很简单,但它隐含的一些类比意义可以启发我们更直观地去理解现代物理中的一些问题:
(1) 与这个故事中的“物理学家”的做法类似,现代物理研究世界的方法一般也是通过在低能态下的观察,总结物理规律,然后预测高能态下的物理现象.
(2) 这些预测的物理现象需要通过实验来证实.有时候隐藏的物理本质只有通过高能态才能被激发出来,比如这个故事中刚体和刚性绳的区别.
(3) 高能量有可能可以激发出新的空间维度,比如这个故事中r的改变而产生的高维空间.
(4) 这个高维空间将低维空间中不同的轨线连接起来,好似我们所说的虫洞现象.
这个启发性的例子从简单形象的角度类比解释了现代物理的空间升降维现象,也反映了数学和物理的紧密联系,适合工科学生的本科教学.作者从2012年开始,一直将此问题用在北京航空航天大学中法工程师学院预科二年级微分方程的课堂教学中,收到了较好的课堂反响.
总之,本文通过对单摆问题的分析,对现代物理中的一些问题给出了形象的类比解释,目标是更好地激发学生对现代物理的学习热情.
[1]BeckerK,BeckerM,SchwarzJ.StringtheoryandM-theory:Amodernintroduction[M].CambridgeUniversityPress, 2007.
[2]FlammL.BeitraegezurEinsteinischengritationstheorie[J].PhysikalischeZeitscrift, 1916, 17: 448.
[3]PokornyP.Stabilityconditionforverticaloscillationof3-dimheavyspringelasticpendulum[J].RegularandChaoticDynamics, 2008,13(3): 155-165.
附录
本文的轨迹相图是在WolframMathematica8.0软件中得到的,绘图语句如下,供读者参考.
图2:
StreamDensityPlot[{y,-Sin[x]},{x,-3[Pi],3[Pi]},{y,-3,3},StreamPoints→Fine,StreamStyle→Directive[Thick,Black],RegionFunction→Function[{x,y}],ColorFunction→"Pastel",AspectRatio→1/[Pi],ImageSize→1200,Frame→True,FrameLabel→{[CapitalTheta],[CapitalTheta]'},FrameStyle→Large]
图3:
StreamDensityPlot[{y,-Sin[x]},{x,-3 [Pi],3 [Pi]},{y,-3,3},StreamPoints→Fine,StreamStyle→Directive[Thick,Black],RegionFunction→Function[{x,y},Cos[x] + y^2 > 0],ColorFunction→"Pastel",AspectRatio→1/[Pi],ImageSize→1200,Frame→True,FrameLabel→{[CapitalTheta],[CapitalTheta]'},FrameStyle→Large]
图4:
StreamDensityPlot[{y,-y - Sin[x]},{x,-3 [Pi],3 [Pi]},{y,-3,3},StreamPoints→Fine,StreamStyle→Directive[Thick,Black],RegionFunction→Function[{x,y}],ColorFunction→"Pastel",AspectRatio→1/[Pi],ImageSize→1200,Frame→True,FrameLabel→{[CapitalTheta],[CapitalTheta]'},FrameStyle→Large]
图5:
StreamDensityPlot[{y,-y - Sin[x]},{x,-3 [Pi],3 [Pi]},{y,-3, 3},StreamPoints→Fine,StreamStyle→Directive[Thick,Black],RegionFunction→Function[{x,y},Cos[x] + y^2 > 0],ColorFunction→"Pastel",AspectRatio→1/[Pi],ImageSize→1200,Frame→True,FrameLabel→{[CapitalTheta],[CapitalTheta]'},FrameStyle→Large]
■
FROM PENDULUM TO THE CHANGE OF SPATIAL DIMENSION
Fang Le1Ge Mingwei2Liu Yangwei3
(1Ecole Centrale de Pekin, Beihang University, Beijing 100191;2School of Renewable Energy, North China Electric Power University, Beijing 102206;3School of Energy and Power Engineering, Beihang University, Beijing 100191)
In order to inspire undergraduate student to intuitively construct pictures for the investigations of modern physics, we describes new physical interpretations to the problem of pendulum, aiming at involving modern physical concepts such as high-dimensional space and wormhole. When the pendulum arm is a rigid string rather than a rigid rod, there will be holes in the phase portraits, which implies the phenomenon of dimension change at boundary. This example is inspiring for the scientific research of modern physics and is suggested to be employed in undergraduate education.
simple pendulum; spatial dimension; modern physics
2016-05-12
国家自然科学基金(11572025,11202013,51420105008).
方乐,男,副教授,主要从事物理和数学教学科研工作,研究方向为流体力学.le.fang@zoho.com
柳阳威,男,副教授,主要从事流体机械教学科研工作,研究方向为流体力学.liuyangwei@126.com
方乐,葛铭纬,柳阳威. 从单摆看空间的升降维现象[J]. 物理与工程,2016,26(6):31-33.

