Buckling and post-buckling analyses of size-dependent piezoelectric nanoplates
Chen Liu,Lio-Ling Ke∗,Jie Yng,Sritwt Kitipornhi,Yue-Sheng Wng
aInstitute of Engineering Mechanics,Beijing Jiaotong University,Beijing 100044,China
bSchool of Aerospace,Mechanical and Manufacturing Engineering,RMIT University,PO Box 71,Bundoora,VIC 3083,AustraliacSchool of Civil Engineering,The University of Queensland,St Lucia,QLD 4072,Australia
Article
Buckling and post-buckling analyses of size-dependent piezoelectric nanoplates
Chen Liua,b,Liao-Liang Kea,∗,Jie Yangb,Sritawat Kitipornchaic,Yue-Sheng Wanga
aInstitute of Engineering Mechanics,Beijing Jiaotong University,Beijing 100044,China
bSchool of Aerospace,Mechanical and Manufacturing Engineering,RMIT University,PO Box 71,Bundoora,VIC 3083,AustraliacSchool of Civil Engineering,The University of Queensland,St Lucia,QLD 4072,Australia
H I G H L I G H T S
·An increasing nonlocal parameter leads to smaller buckling and post-buckling loads.
·The positive/negative electric voltage decreases/increases buckling and post-buckling loads.
·A relatively large temperature rise results in slight drops in buckling and post-buckling loads.
A R T I C L E I N F O
Article history:
Received 18 September 2016
Accepted 28 October 2016
Available online 15 November 2016
Piezoelectric nanoplates
Buckling
Post-buckling
Nonlocal theory
Size effect
This paper attempts to investigate the buckling and post-buckling behaviors of piezoelectric nanoplate based on the nonlocal Mindlin plate model and von Karman geometric nonlinearity.An external electric voltage and a uniform temperature rise are applied on the piezoelectric nanoplate.Both the uniaxial and biaxial mechanical compression forces will be considered in the buckling and post-buckling analysis.By substituting the energy functions into the equation of the minimum total potential energy principle, the governing equations are derived directly,and then discretized through the differential quadrature (DQ)method.The buckling and post-buckling responses of piezoelectric nanoplates are calculated by employing a direct iterative method under different boundary conditions.The numerical results are presented to show the influences of different factors including the nonlocal parameter,electric voltage, and temperature rise on the buckling and post-buckling responses.
©2016 The Author(s).Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).
1.Introduction
Beam or plate type piezoelectric nanostructures have been extensively applied in many branches of nano-electro-mechanical systems(NEMS,e.g.nanoresonator,nanogenerator,light-emitting diodes,chemicalsensors,etc.),thusresearchesonthepiezoelectric nanostructures have been active research fields with worldwide attention[1–3].In practical applications,it is common for the beam or plate type components of nanodevices to suffer in-plane compressive loadings,which may cause buckle failure of the nanostructures,thus studies on the buckling and post-buckling behaviors of the piezoelectric nanostructures are important in the design of nanodevices.
Compared with their macroscale counterparts,piezoelectric nanostructures are found of possessing superior thermal,electrical,mechanical,and other physical/chemical properties[4,5]. As generally believed,the size-dependent properties become significant as the dimensions of the nanostructures vary from several hundred nanometers to just a few nanometers.Both experiments and atomic simulations[6,7]show valid evidences of the fact that the long-range inter atomic and inter molecular cohesive forces gain significant and non-ignorable influences on the mechanical properties when the length scale reduces.It is well-known that the nonlocal theory raised by Eringen[8–10]is considered as an effective theory to characterize the size effect of nanostructures.Unlike the classical size-independent continuum theory,the nonlocal theory introduces the internal length scale into the constitutive equations to account the scale effect in micro-and nano-scaled structures.The key point in the nonlocal theory is that,at a reference point,the stress depends on not only the strain component at the point,but also all the strain components in the domain around.Such proposal is widely accepted to study the size-dependent properties of nanostructures,including the bending[11–14],buckling and post-buckling[15–18],linear and nonlinear vibrations[19–24],and wave propagation characteristics[25,26]of carbon nanotubes,graphene sheets,nanowires, etc.
Besides the analysis of elastic nanostructures mentioned above,applications of the nonlocal theory already have been extended to the size-dependent electro-mechanical analysis of the piezoelectric nanostructures in recent years.Ke and his coauthors have examined the free vibration behavior of nonlocal piezoelectric nanoplates by deriving analytical solutions based on the Kirchhoff plate theory[27]and numerical solutions based on the Mindlin plate theory[28].The nonlocal plate model is also employed by Asemi and his co-authors to study the vibration characteristics of piezoelectric nanoplate systems embedded in Pasternak elastic medium[29]and of double piezoelectric nanoplate systems with initial stress[30].Arani and his coauthors[31–34]presented comprehensive investigations on the boron nitride nanotubes(BNNTs)by using nonlocal nanobeam and nanoshell models,to study the buckling,linear,and nonlinear vibrations under electro-mechanical environments.Wang and Wang[35]examined the bending behavior of a piezoelectric nanowire.Their study included both the surface effect and size effect by using the surface elasticity theory and nonlocal theory. Zhang et al.[36]also considered both nonlocal effect and surface effect in the analysis of the dispersion characteristics of the elastic wave propagating in a monolayer piezoelectric nanoplate.
For the piezoelectric nanoplate subjected to in-plane loadings on its edges,the compression forces may result in nonlinear deformation at high loading levels.To accurately predict the post-buckling response in such cases,the geometrical nonlinearity should be considered as an essential influencing factor on the post-buckling performance.Some investigations have been already presented in the field of nonlinear analysis on the piezoelectric nanostructures.Based on the von Karman type nonlinear displacement–strain relationship,Ke and his co-authors investigated the nonlinear vibration[37]and post-buckling[38]behaviors of nonlocal Timoshenko piezoelectric nanobeams under combined thermo-electro-mechanical loadings.The von Karman nonlinear equations are also applied by Asemi et al.[39]to establish an analytical procedure to investigate nonlinear vibration and post-buckling behaviors of piezoelectric nano-electro-mechanical resonators based on the simply supported Kirchhoff piezoelectric nanofilm(PNF)model.More recently,based on the nonlocal Kirchhoff plate theory,Liu et al.[40]presented the analytical study on the nonlinear vibration of the simply supported piezoelectric nanoplates rested on Winkler foundations.
This paper attempts to investigate the buckling and postbuckling behaviors of the piezoelectric nanoplates subjected to combined thermo-electro-mechanical loadings based on the nonlocal theory,Mindlin plate theory and von Karman geometric nonlinearity.Byusingtheprincipleofminimumtotalpotentialenergy, the nonlinear governing equations and corresponding boundary conditions can be derived.The equations are then discretized by using the differential quadrature(DQ)method and solved by a direct iterative method to determine the buckling and post-buckling responsesofpiezoelectricnanoplateswithdifferentboundaryconditions.Parametric studies are presented to show the influences of the nonlocal parameter,electric voltage and temperature rise on the size-dependent buckling and post-buckling responses.
2.Nonlocal theory for piezoelectric materials
The traditional local elasticity is size independent,thus it fails to predict the mechanical properties of nanostructures.The nonlocal theory raised by Eringen[8–10]overcomes the shortage by introducing a simple physical concept that the component of stresstensoratacertainpointisafunctionnotonlyofstraintensor at the point but also of strain tensors in the domain.Recently, Ke and his co-authors[27,28]presented some works applying the nonlocal theory in the analysis of piezoelectric nanostructures. AccordingtoKeetal.[27,28],thenonlocalconstitutiverelationsfor the piezoelectric solids may be expressed in differential forms as
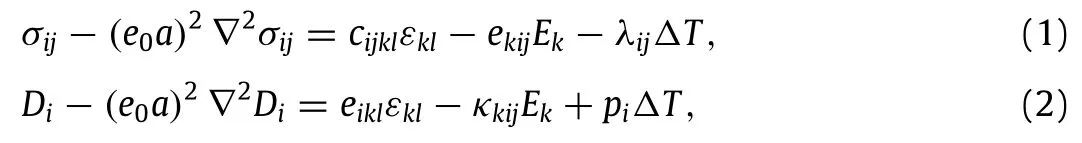
whereσij,εij,Di,andEiare the componentsof stress,strain,electric displacement,and electric field,respectively;cijkl,ekij,κkij,λij,andpiare the elastic constant,piezoelectric constant,dielectric constant,thermal modulus,and pyroelectric constant,respectively; ΔTis the temperature rise;∇2is the Laplacian operator;e0ais the scale coefficient incorporating the size effect on the response of structures in nanosize whereais an internal characteristic length (e.g.,lattice parameter,granular size).The parametere0is essentialforthevalidityofnonlocalmodels,whichcanbedeterminedby matchingthedispersioncurvesbasedontheatomiccurves.Specifically,for the piezoelectric nanoplates,the nonlocal relations can be approximated as
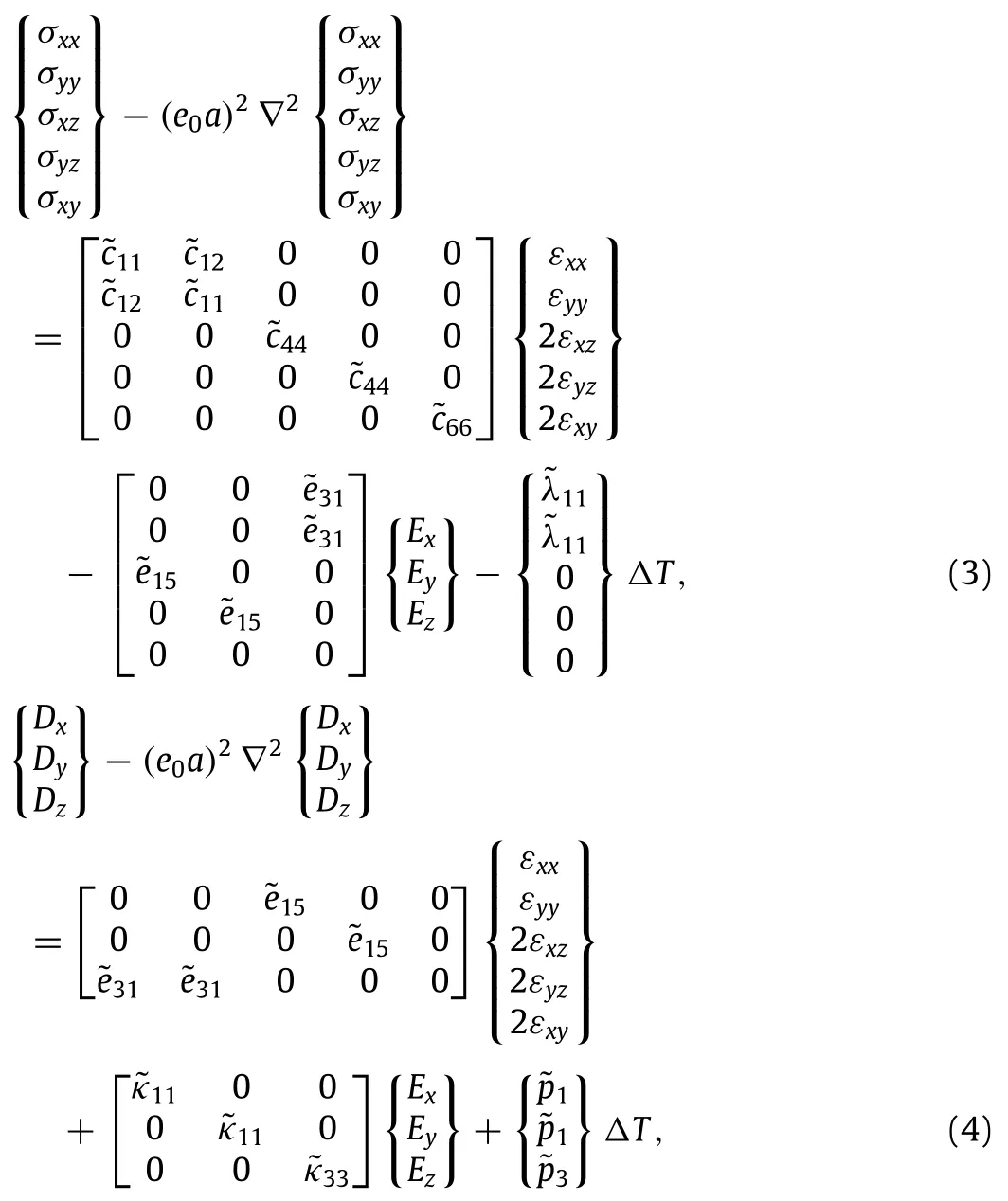
where˜cij,˜eij,˜κij,˜λij,and˜piare respectively the reduced elastic constants,piezoelectric constants,dielectric constants,thermal moduli,and pyroelectric constants for the piezoelectric nanoplate under the plane stress state[41,42].These constants are given as
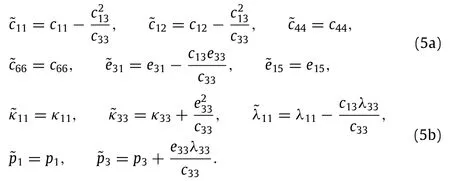
3.Buckling and post-buckling of piezoelectric nanoplates
As shown in Fig.1,a nonlocal continuum model is developed for the buckling and post-buckling analyses of the piezoelec-tric nanoplate with lengthla,widthlb,and thicknessh.Suppose the piezoelectric nanoplate is subjected to an external voltage ˜Φ(x,y,z),a uniform temperature riseΔTand biaxial compression forcesPxandPy.According to the Mindlin plate theory,the displacement of an arbitrary point along thex-,y-,andz-axis,denoted asu1(x,y,z),u2(x,y,z),andu3(x,y,z),can be expressed as
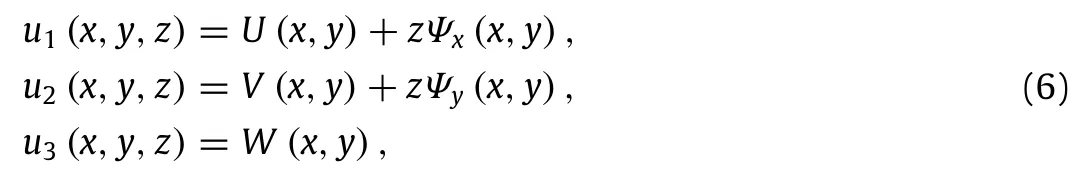
whereU(x,y)andV(x,y)are the in-plane displacements alongx-andy-direction of the mid-plane;W(x,y)is the out-plane displacement of the mid-plane;Ψx(x,y)andΨy(x,y)are the rotation angles of the nanoplate cross-sections in thexoz-andyoz-planes, respectively.Through the von Karman nonlinearity,the strain–displacement relations of the piezoelectric nanoplate can be given by

To confirm the Maxwell equation,the distribution of external electric potential for the present nanoplate model is assumed as a combination of a cosine and linear variation[28,43]
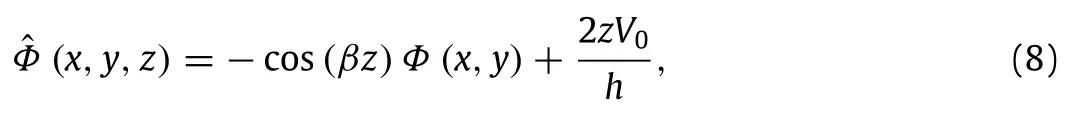
whereβ= π/h;Φ(x,y)is the spatial and time vibration of the electric potential in the mid-plane of the nanoplate,andV0is the external electric voltage.Then the components of electric field can be written as
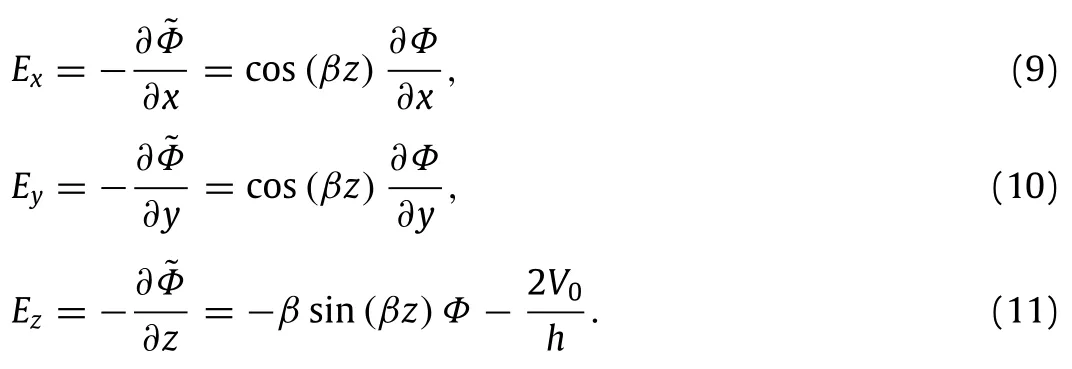
The strain energyΠsthen can be expressed as
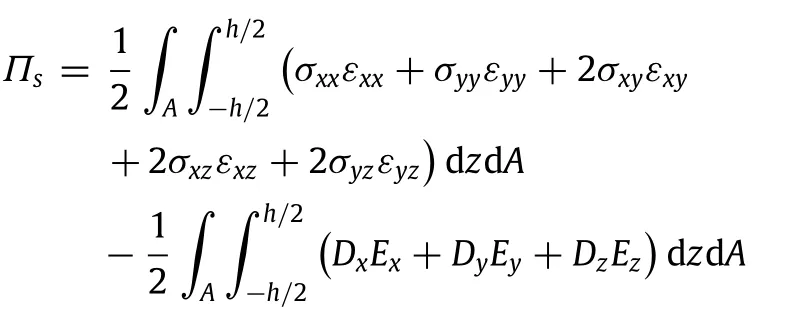
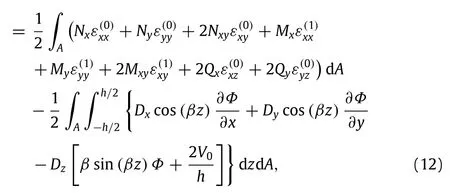
whereAdenotes the domain occupied by the mid-plane of the nanoplate;the normal resultant forcesNxandNy,twisting shear forceNxy,shearing forcesQxandQy,bending momentsMxandMy, and twisting momentMxyare separately calculated from
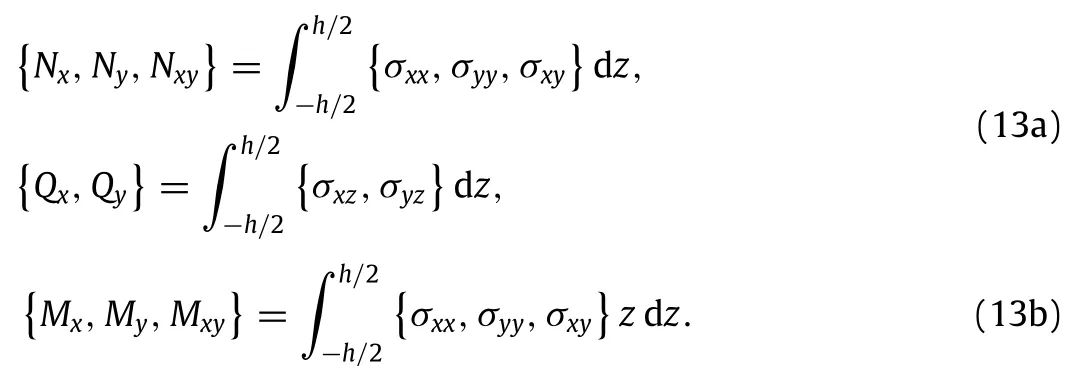
The work done by the uniform distributed external biaxial compression forcesPxandPy,denoted byΠP,can be expressed as
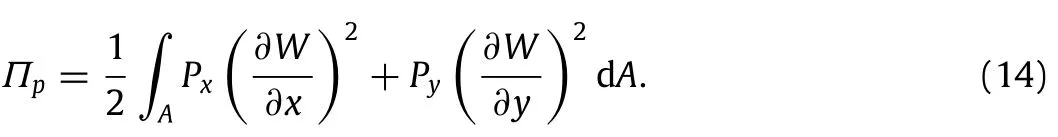
To derive the governing equations,we substitute the energy Eqs. (12)and(14)into the principle of minimum total potential energy,

whereδdenotes a variational operator.Then the governing equations of motion can be derived by setting the coefficients of δU,δV,δW,δΨx,δΨy,andδΦto zero
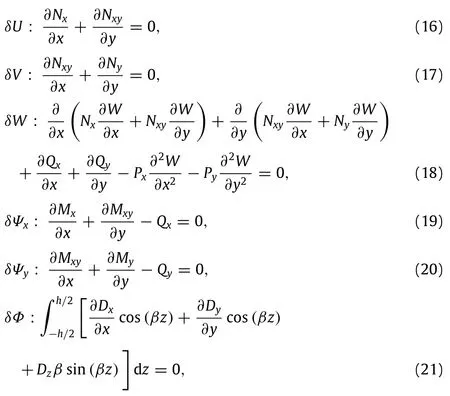
and the corresponding boundary conditions are also obtained as
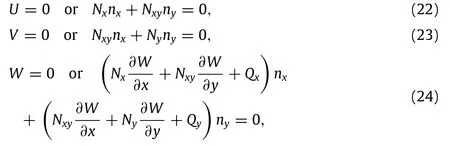
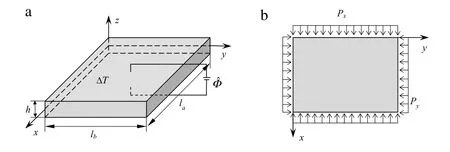
Fig.1.Schematic configuration of a piezoelectric nanoplate.
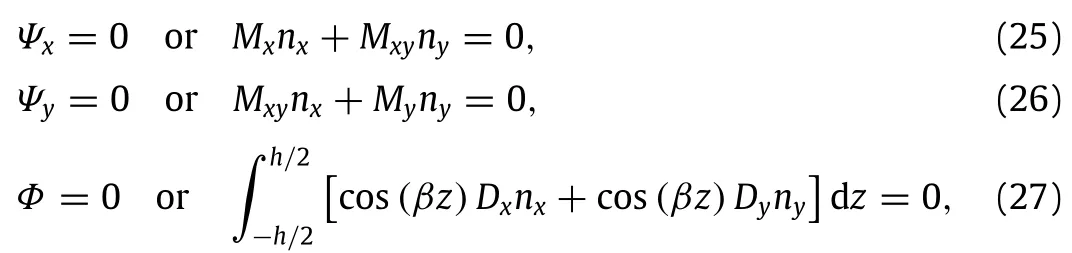
where(nx,ny)denotes the direction cosines of the outward unit normal to the boundary of the mid-plane.
From the constitutive Eqs.(3)and(4),we have

whereks=5/6 is the shear correction factor of the rectangular nanoplate,and the coefficients can be expressed respectively,
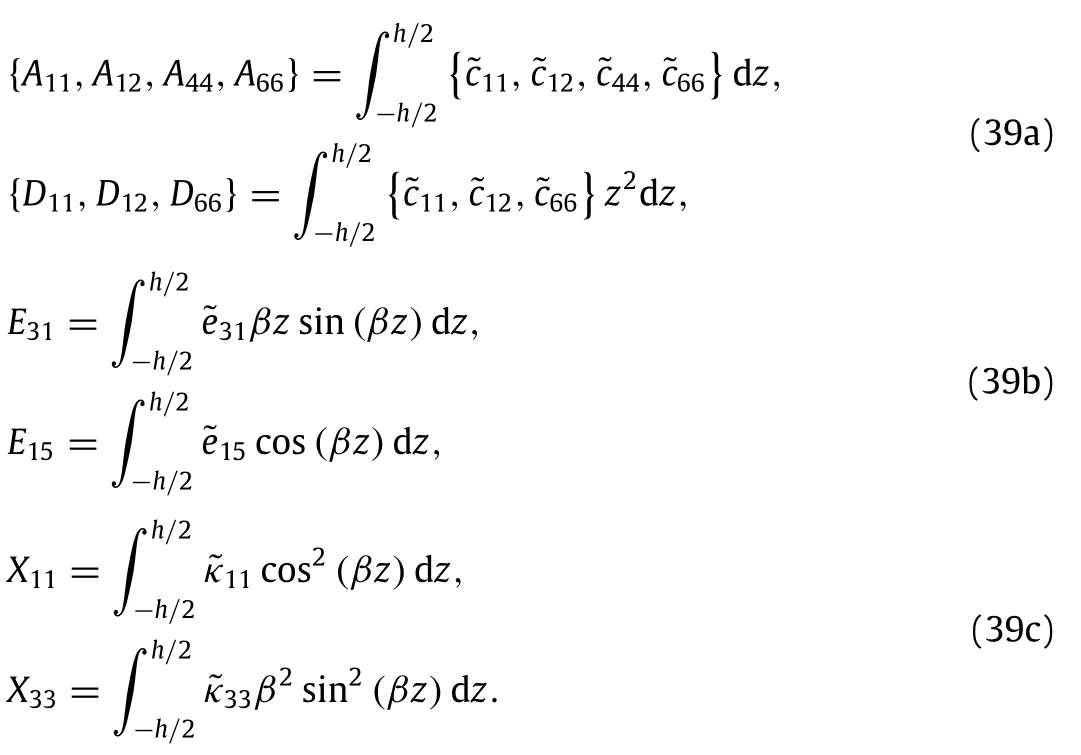
By substituting Eqs.(28)–(38)into Eqs.(16)–(21),the governing equations can be rewritten in forms as
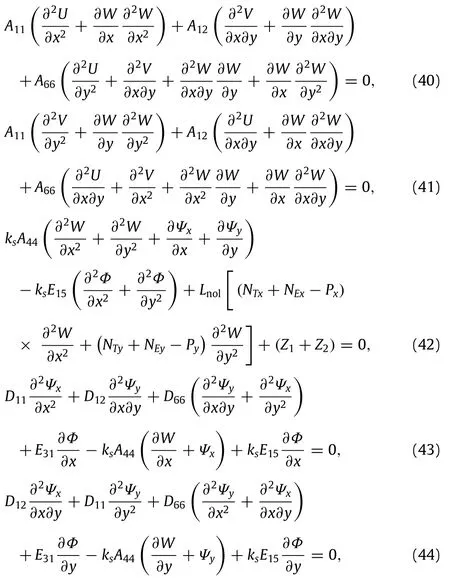

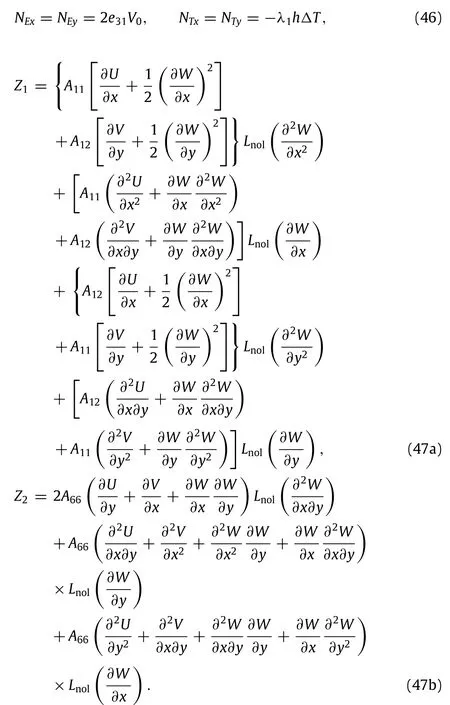
By introducing the following dimensionless quantities
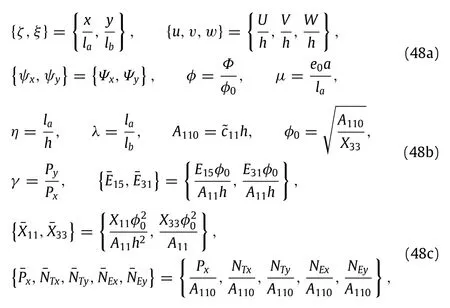
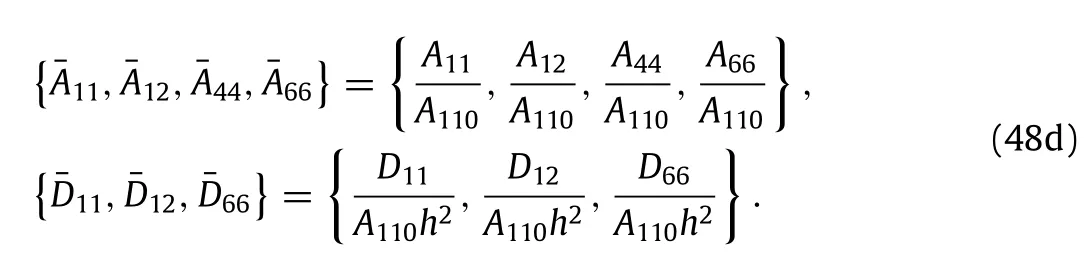
Equations(40)–(45)can be transformed into the dimensionless equations as

where
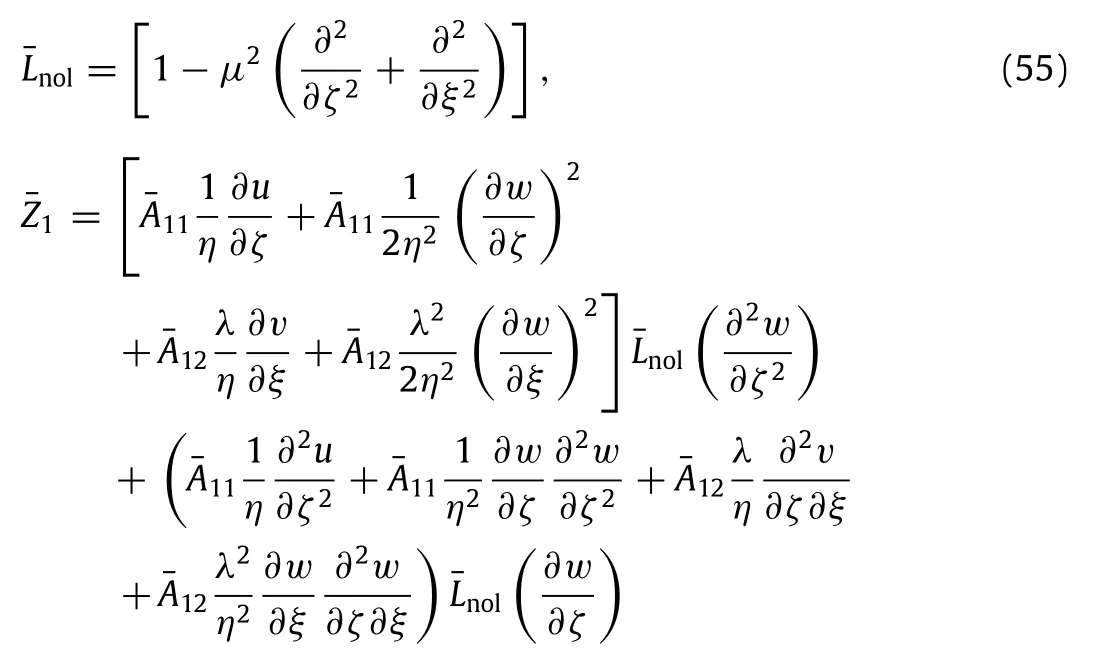

Assume the electric potential is zero at all edges of the piezoelectric nanoplate,and the boundary conditions are considered in following cases:
Case1:The piezoelectric nanoplate is simply supported at all four edges with no limitations on the in-plane displacement along the normal direction of each edge,referred as SSSS.
Case2:Two adjacent edges of the piezoelectric nanoplate are simply supported and the other two are clamped,with all edges freely moveable on their normal directions,referred as CCSS.
Case3:The four edges piezoelectric nanoplate are all clamped with no limitations on the in-plane displacement along the normal direction of each edge,referred as CCCC.
The cases of boundary conditions mentioned above can be separately expressed in the non-dimensional form as:


4.Solution method
To obtain the postbuckling behaviors,the DQ method and iterative technique are employed to solve the nonlinear governing equations.According to DQ method,the piezoelectric nanoplate can be discretized in the domain byN1grid points along theζ-axis andN2grid points along theξ-axis,and the values ofu,v,w,ψx, ψy,andφand theirk1th andk2th partial derivatives with respect toζandξ,respectively,can be approximated by
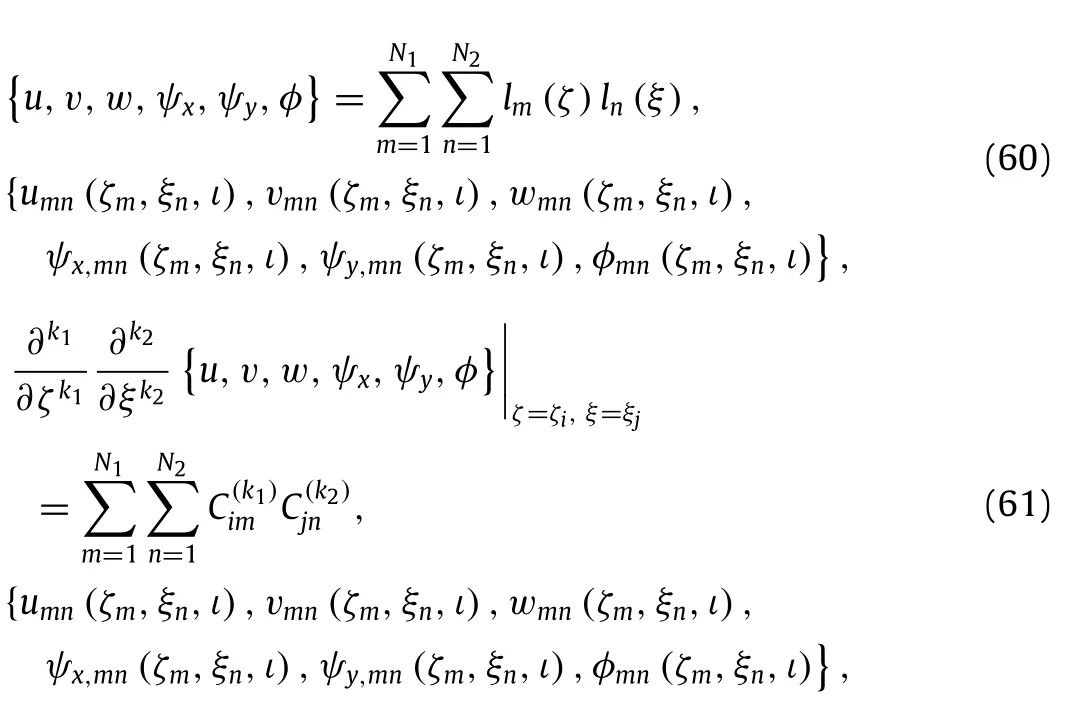
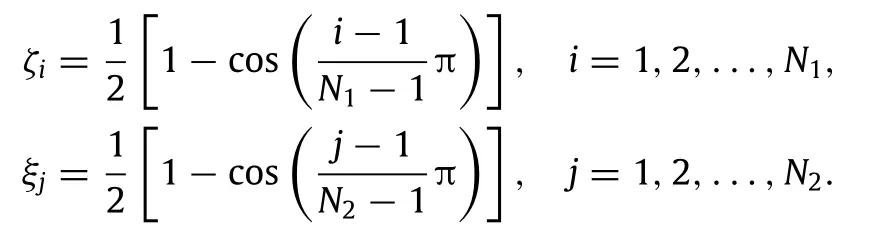
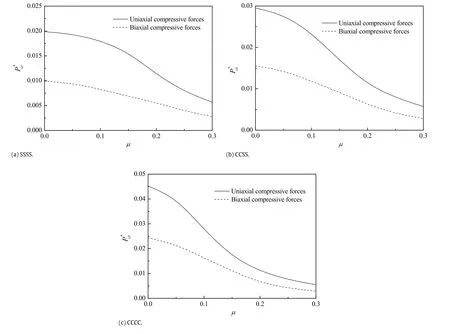
Fig.2.Effect of the nonlocal parameterµon the dimensionless critical buckling load P∗crof the piezoelectric nanoplate.
Applying the Eqs.(60)and(61)into the governing Eqs.(49)–(54)yields the following ordinary differential equations
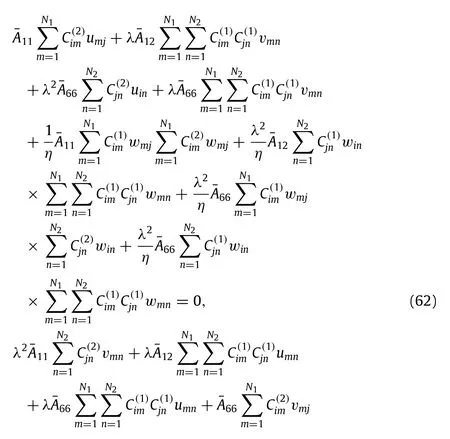

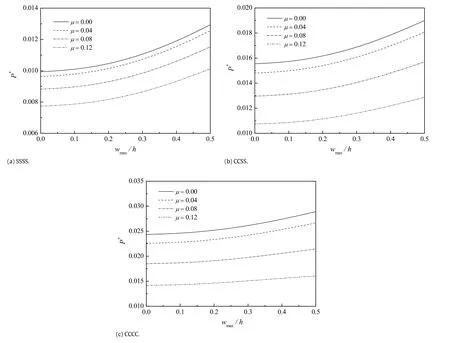
Fig.3.Effect of the nonlocal parameterµon the dimensionless post-buckling response of the piezoelectric nanoplate.


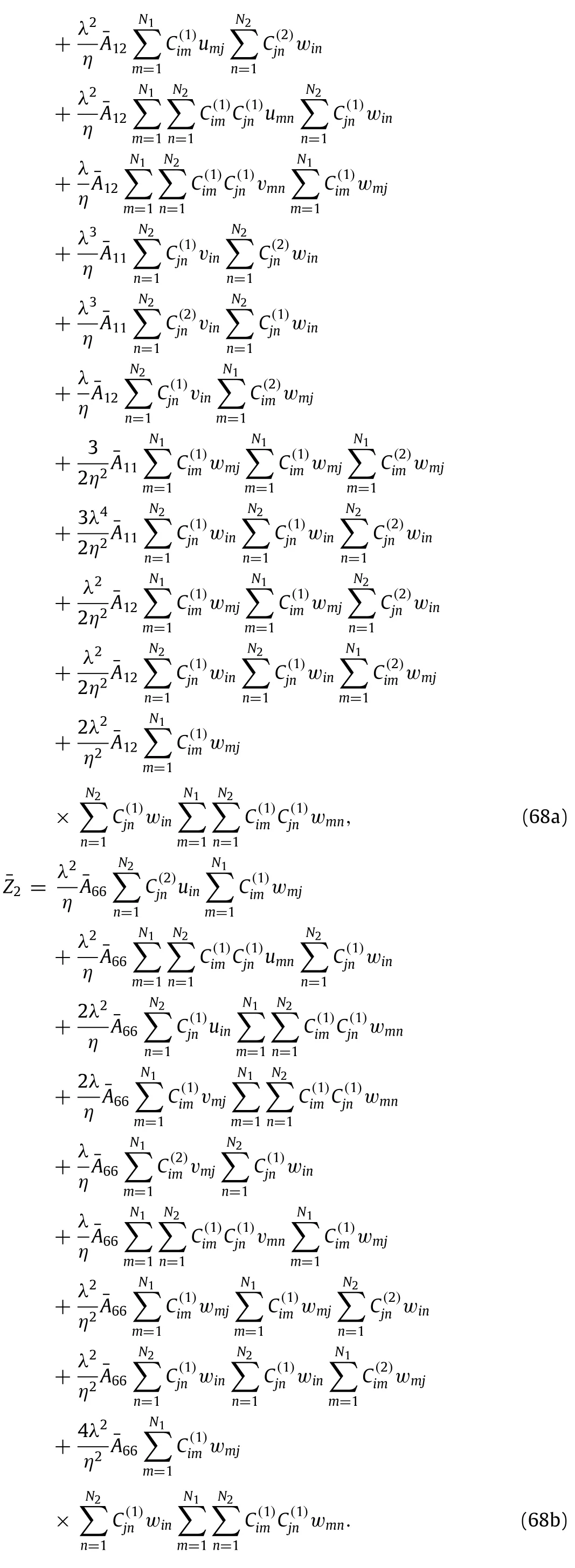
Correspondingly,the boundary conditions can be rewritten as

for an SSSS piezoelectric nanoplate;

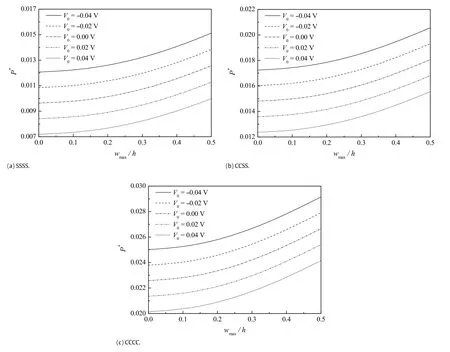
Fig.4.Effect of the external electric voltage V0on the dimensionless post-buckling response of the piezoelectric nanoplate.
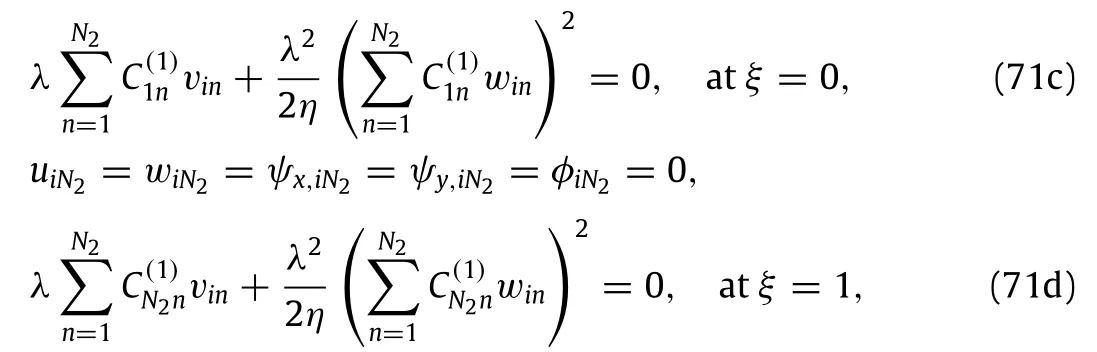
for a CCCC piezoelectric nanoplate.
The unknown quantities can be denoted in the vector form as
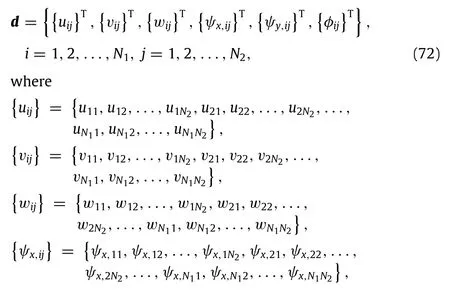
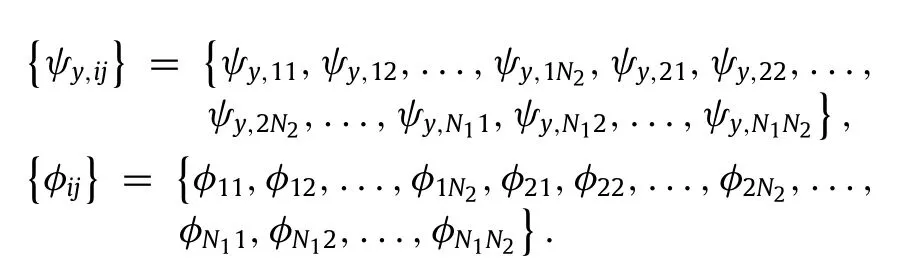
Then the governing Eqs.(62)–(67),together with the boundary conditions,can be written in the matrix form as

where KLand KNLare separately the linear and nonlinear stiffness matrices,and KGis the geometric stiffness matrix;P∗represents the post bucking load.KL,KNLand KGare all 6N1N2× 6N1N2matrices.Here,Eq.(73)can directly reduce to a linear static buckling eigenvalue problem of the piezoelectric nanoplate if the nonlinear stiffness matrix is neglected,which is given by

where the dimensionless critical buckling loadand the corresponding mode shape can be obtained.
The post-buckling response of the piezoelectric nanoplate can becalculatedbysolvingEq.(73)throughadirectiterativeprogress. Firstly,the iterative scheme begins by solving an eigenvalue problem of Eq.(74)without considering the geometric nonlinearity to obtain the eigenvalue and corresponding eigenvector as the initial
Fig.5.Effect of the temperature changeΔT on the dimensionless post-buckling response of the piezoelectric nanoplate.
guesses for the buckling load and mode shape.Then,the eigenvector is approximately scaled up to a given value of transverse vibrationamplitudetocalculatethenonlinearmatrixoranew eigenvalue system.Afterwards,a new eigenvalue and the associated eigenvector can be figured out from the updated eigenvalue system.Theprogressshouldberepeateduntiltherelativeerrorbetween the eigenvalues obtained from two consecutive iterations is within 0.1%for the final result of the post-buckling behaviors.
5.Numerical results and discussion
In this section,the buckling and post-buckling loads are solved for the piezoelectric nanoplates subjected to uniaxial and biaxial in-plane mechanical loadings.A numerical study is conducted to examine the effects of the nonlocal parameter,electric voltage and temperature rise on the buckling and post-buckling behaviors of the piezoelectric nanoplate.Following our previous work, PZT-4 is chosen as the material of the piezoelectric nanoplate with material properties listed in Table 1,and unless otherwise stated, the piezoelectric nanoplate is assumed to be measured of lengthla=70 nm,widthlb=70 nm and thicknessh=5 nm.
5.1.Comparison and convergence studies
Theverificationofaccuracystudyofthepresentanalysisshould befirstlycarriedoutbeforefurtherdetaileddiscussion.Table2lists the results of the dimensionless buckling and post-buckling loads of the piezoelectric nanoplate subjected to biaxial compression forces with varying total numberNof grid points.Without loss of generality,we set same number of grid points alongζ-and ξ-axis,namelyN1=N2=N.Both the influences of external electric voltage and temperature change are neglected here and the nonlocal parameter is assumed to beµ = 0.04.For the post-buckling analysis,the maximum deflection is considered as wmax/h= 0.3.It is obvious that the accuracy of the present results improves with an increasing number of grid points,and is convergentatN=11.Hence,N=11isusedinallofthefollowing numerical calculations.
Ignoring the nonlocal effect,piezoelectric effect and the von Karman nonlinearity,the present piezoelectric nanoplate can directly reduce to a macroscopic Mindlin plate model.Table 3 presents the results of dimensionless buckling coefficient of isotropic square plates with all edges simply supported(SSSS). The present results are compared with the results obtained by Wang et al.[45]analytically based on the Mindlin plate theory and by Liew et al.[46]numerically through the three-dimensional approximation.Here,the dimensionless plate buckling coefficient is defined asλcr=Pcrb2/(π2D),and the Poisson’s ratio is assumed to beν=0.3.Clearly,with varying thickness to side ratios,the results of buckling coefficients in different studies keep in good accordanceunderboththeuniaxialandbiaxialcompressionforces.
Fig.6.Effect of aspect ratioλ=la/lbon the dimensionless post-buckling response of the piezoelectric nanoplate.
Table 4 presents the comparison of the dimensionless postbuckling coefficient of isotropic square plates between the results of Wu et al.[47]and present study.The dimensionless postbuckling coefficients here is defined asλx=Pxb2/(π2D).Assume that the plate is subjected to uniaxial compression forces alongx-direction,and that the side-to-thickness ratio isla/h= 40. Alumina is taken as the material of the plate with elastic modulusE=380 GPa and Poisson’s ratioν=0.3.It is seen that the results are in good agreement with acceptable errors.
5.2.Buckling and post-buckling analyses
Figure 2 gives the effect of the nonlocal parameterµ on the dimensionless critical bucking loadP∗crof the piezoelectric nanoplates subjected to uniaxial and biaxial compression forces, respectively.Here,neither the influences of external electric voltage nor that of temperature rise is considered.Obviously,as the nonlocal parameterµincreases,the critical buckling loadP∗cr drops significantly,which indicates that the existence of nonlocal effecttendstodecreasethestiffnessofthepiezoelectricnanoplate, and hence decreases the critical buckling load.Also,it can be concluded from the curves that,with greater limitation of the clamped end,the critical buckling loadP∗crbecomes larger than that of simply supported end.However,with higher value of the nonlocal parameterµ,the difference between the two boundary conditions diminishes gradually.
The curves in Fig.3 present the effect of the nonlocal parameter µonthedimensionlesspost-bucklingresponseofthepiezoelectric nanoplates under biaxial compression forces without influences of the external electric voltage(V0=0 V)and temperature rise (ΔT=0 K).Obviously,the post-buckling response of the piezoelectric nanoplate is a typical bifurcation problem,in which the bifurcation point represents the critical buckling loads.With a larger value of the maximum deflectionwmax,the post-buckling load also shows an upward trend.Note that the nonlocal parameterµ=0 correspondstotheclassicalnonlinearpiezoelectricnanoplates.Itis clearlyobservedthatthepost-bucklingloadscalculatedbypresent nonlocal piezoelectric nanoplates are smaller than those predicted by the classical piezoelectric plate models,and that as the nonlocal parameterµincreases,considerable drops can be found in the post-buckling loads.This is due to the fact that the stiffness of the piezoelectric nanoplate tends to reduce when the nonlocal effect is considered,and hence the post-buckling loads are depressed.
Examined in Fig.4 is the effect of external electric voltageV0on the post-buckling response of the piezoelectric nanoplates.The nonlocal parameter is taken asµ =0.04,and the temperature rise is taken asΔT= 0 K.Obviously,the electric voltage is a sensitive influencing factor for the post-buckling behaviors of the piezoelectric nanoplate.Although the electric voltage only slightly grows from-0.04 V to 0.04 V,notable drop still can be found in the curves of post-buckling loads versus deflection. Thepositive/negativeexternalelectricvoltagecangeneratebiaxial compressive/tensile forces in the body of piezoelectric nanoplate,which in turn significantly decreases/increases the buckling load and post-buckling strength of the piezoelectric nanoplates.
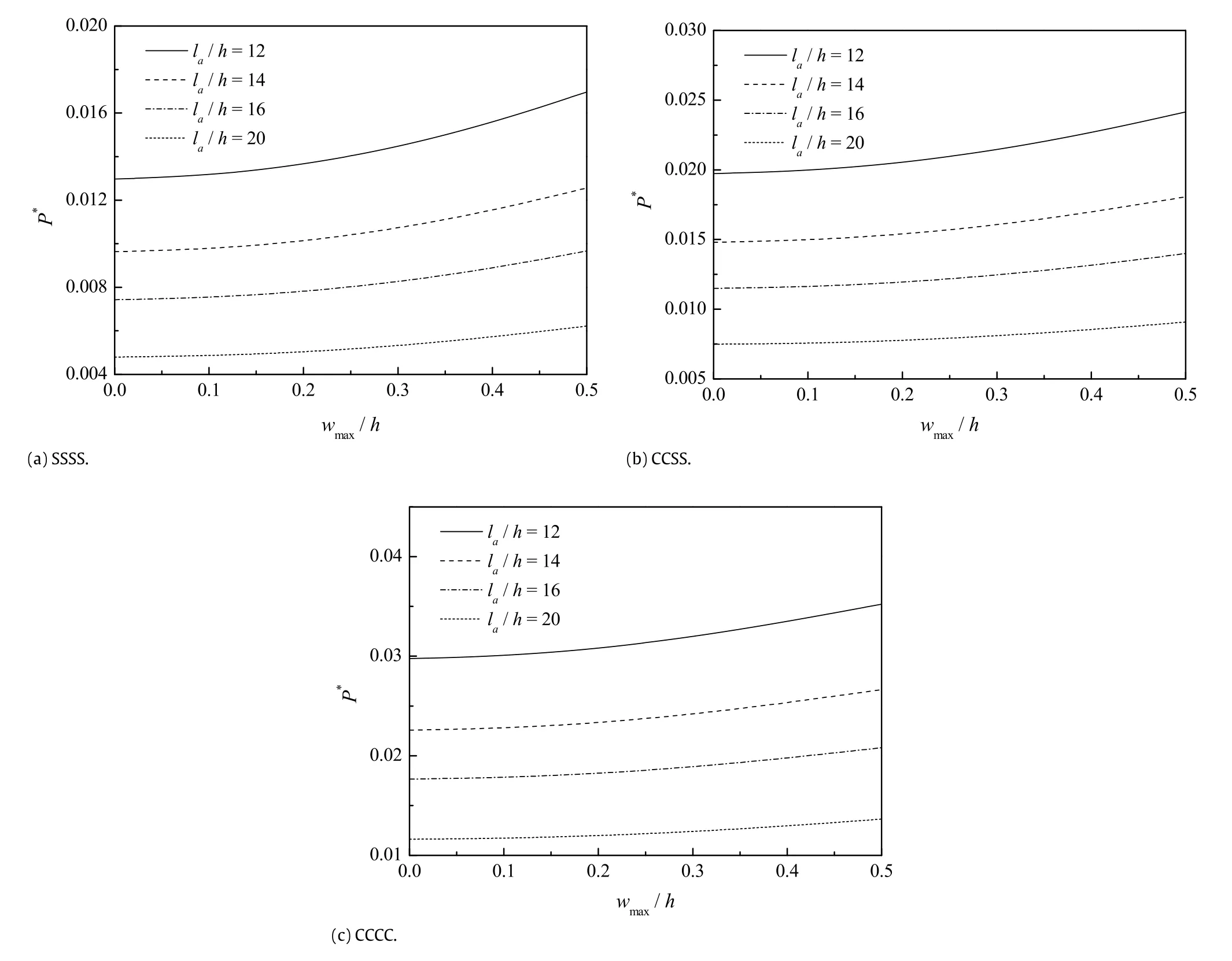
Fig.7.Effect of side-to-thickness ratioη=la/h on the dimensionless post-buckling response of the piezoelectric nanoplate.

Table 1 Material properties of PZT-4.
Table 2 Dimensionless buckling loadsfor piezoelectric nanoplates with varying node numbers N.

Table 2 Dimensionless buckling loadsfor piezoelectric nanoplates with varying node numbers N.

Table 3 Comparison of the buckling coefficientsλcrof square elastic SSSS plates under uniaxial and biaxial compressive forces.
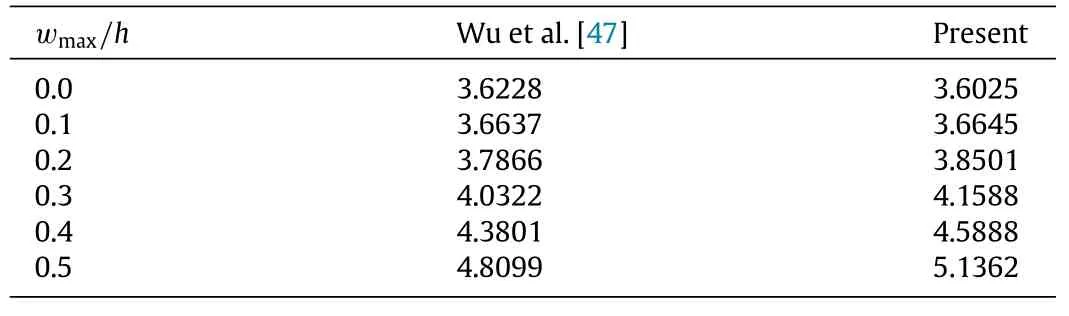
Table 4 Comparison of the post buckling coefficientsλxof SSSS plates under uniaxial compressive forces.
Figure 5 plots the effects of the temperature riseΔTon the post-buckling responses of the piezoelectric nanoplates with µ = 0.04 andV0= 0 V.For a given maximum deflection wmax,the temperature rise will result in a slight decrease on the buckling and post-buckling loads.However,unlike the electric voltages,the temperature change only has very limited influences on the buckling and post-buckling behaviors of the piezoelectric nanoplate.Even the temperature rise varies from 0 to 300 K, there are merely minor variations that can be found in the postbuckling load versus deflection curves.Such phenomenon is the resultofthatPZT-4possessesasmallthermalmodulus,whichdoes not transform the temperature into stress in the body effectively. If we alter the piezoelectric material to another one with large thermal modulus,it is predictably that the temperature rise can also become a sensitive factor on the vibration behavior.
The effects of the aspect ratioλ=la/lband side-to-thickness ratioη=la/hontheirpost-bucklingresponsesofthepiezoelectric nanoplates are shown in Figs.6 and 7,respectively,withµ = 0.04,V0=0 V,andΔT=0 K.Obviously,the size variation of piezoelectric nanoplates can be sensitive factors influencing their post-buckling behaviors.With growing value of the aspect ratioλ,significant improvements of the post-buckling loads can be found in the post-buckling response curves of the piezoelectric nanoplates.Such phenomenon indicates that larger aspect ratioλ of the piezoelectric nanoplate strengthens its stiffness.However, growth in the side-to-thickness ratioη =la/hwill directly reduce the stiffness of piezoelectric nanoplates,hence result in remarkable reduction in the post-buckling loads of piezoelectric nanoplates.
6.Conclusions
This paper investigates the buckling and post-buckling responses of the piezoelectric nanoplates subjected to combined thermo-electro-mechanical loadings based on the Mindlin plate theory,thenonlocaltheoryandthevonKarmannonlinearity.From the numerical results,we can conclude:(1)An increasing nonlocal parameter will reduce the stiffness of the piezoelectric nanoplate, which leads to both smaller critical buckling loads and smaller post-buckling strength.(2)The positive/negative electric voltage weakens/enhances the stiffness of the piezoelectric nanoplates significantly,and decreases/increases the critical buckling loads and post-buckling strength.(3)The temperature rise,unlike the electric voltage,is quite insensitive factor that a relatively large growing in temperature rise results in slight drops in the critical buckling loads and post-buckling strength.
Acknowledgment
The work described in this paper is supported by the National Natural Science Foundation of China(11272040 and 11322218).
[1]Z.W.Pan,Z.R.Dai,Z.L.Wang,Nanobelts of semiconducting oxides,Science 291 (2001)1947–1949.
[2]S.M.Tanner,J.M.Gray,C.T.Rogers,et al.,High-Q GaN nanowire resonators and oscillators,Appl.Phys.Lett.91(2007)203117.
[3]U.Galan,Y.R.Lin,G.J.Ehlert,et al.,Effect of ZnO nanowire morphology on the interfacial strength of nanowire coated carbon fibers,Compos.Sci.Technol.71 (2011)946–954.
[4]Z.L.Wang,ZnO nanowire and nanobelt platform for nanotechnology,Mater. Sci.Eng.R 64(2009)33–71.
[5]S.Xu,Z.L.Wang,One-dimensional ZnO nanostructures:solution growth and functional properties(invited review),Nano Res.4(2011)1013–1098.
[6]C.Q.Chen,Y.Shi,Y.S.Zhang,et al.,Size dependence of Young’s modulus in ZnO nanowires,Phys.Rev.Lett.96(2006)075505.
[7]G.Stan,C.V.Ciobanu,P.M.Parthangal,et al.,Diameter-dependent radial and tangential elastic moduli of ZnO nanowires,Nano Lett.7(2007)3691–3697.
[8]A.C.Eringen,Nonlocal polar elastic continua,Internat.J.Engrg.Sci.10(1972) 1–16.
[9]A.C.Eringen,On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves,J.Appl.Phys.54(1983)4703–4710.
[10]A.C.Eringen,Nonlocal Continuum Field Theories,Springer-Verlag,New York, 2002.
[11]J.N.Reddy,Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates,Internat.J.Engrg.Sci.48(2010) 1507–1518.
[12]Y.M.Xu,H.S.Shen,C.L.Zhang,Nonlocal plate model for nonlinear bending of bilayer graphene sheets subjected to transverse loads in thermal environments,Compos.Struct.98(2013)294–302.
[13]M.E.Golmakani,J.Rezatalab,Nonlinear bending analysis of orthotropic nanoscale plates in an elastic matrix based on nonlocal continuum mechanics, Compos.Struct.111(2014)85–97.
[14]M.Sobhy,Thermomechanical bending and free vibration of single-layered graphene sheets embedded in an elastic medium,Physica E 56(2014) 400–409.
[15]S.C.Pradhan,T.Murmu,Small scale effect on the buckling analysis of singlelayered graphene sheet embedded in an elastic medium based on nonlocal plate theory,Physica E 42(2010)1293–1301.
[16]H.S.Shen,C.L.Zhang,Torsional buckling and postbuckling of double-walled carbon nanotubes by nonlocal shear deformable shell model,Compos.Struct. 92(2010)1073–1084.
[17]A.M.Zenkour,M.Sobhy,Nonlocal elasticity theory for thermal buckling of nanoplates lying on Winkler-Pasternak elastic substrate medium,Physica E 53(2013)251–259.
[18]H.S.Shen,Nonlocal shear deformable shell model for torsional buckling and postbuckling of microtubules in thermal environments,Mech.Res.Comm.54 (2013)83–95.
[19]S.C.Pradhan,A.Kumar,Vibrationanalysisoforthotropicgraphenesheetsusing nonlocalelasticitytheoryanddifferentialquadraturemethod,Compos.Struct. 93(2011)774–779.
[20]R.Ansari,B.Arash,H.Rouhi,Vibration characteristics of embedded multilayered graphene sheets with different boundary conditions via nonlocal elasticity,Compos.Struct.93(2011)2419.
[21]S.Hosseini-Hashemi,M.Zare,R.Nazemnezhad,An exact analytical approach for free vibration of Mindlin rectangular nano-plates via nonlocal elasticity, Compos.Struct.100(2013)290–299.
[22]L.L.Ke,Y.Xiang,J.Yang,et al.,Nonlinear free vibration of embedded double-walledcarbonnanotubesbasedonnonlocalTimoshenkobeamtheory, Comput.Mater.Sci.47(2009)409–417.
[23]J.Yang,L.L.Ke,S.Kitipornchai,Nonlinearfreevibrationofsingle-walledcarbon nanotubes using nonlocal Timoshenko beam theory,Physica E 42(2010) 1727–1735.
[24]L.Shen,H.S.Shen,C.L.Zhang,Nonlocal plate model for nonlinear vibration of single layer graphene sheets in thermal environments,Comput.Mater.Sci.48 (2010)680–685.
[25]Q.Wang,V.K.Varadan,Application of nonlocal elastic shell theory in wave propagation analysis of carbon nanotubes,Smart Mater.Struct.16(2007) 178–190.
[26]A.L.Chen,Y.S.Wang,L.L.Ke,et al.,Wave propagation in nanoscaled periodic layered structures,J.Comput.Theor.Nanosci.10(2013)2427–2437.
[27]C.Liu,L.L.Ke,Y.S.Wang,et al.,Thermo-electro-mechanical vibration of piezoelectric nanoplates based on the nonlocal theory,Compos.Struct.106 (2013)167–174.
[28]L.L.Ke,C.Liu,Y.S.Wang,Free vibration of nonlocal piezoelectric nanoplates under various boundary conditions,Physica E 66(2015)93–106.
[29]S.R.Asemi,A.Farajpour,Thermo-electro-mechanical vibration of coupled piezoelectric nanoplate systems under non-uniform voltage distribution embedded in Pasternak elastic medium,Curr.Appl.Phys.14(2014)814–832.
[30]S.R.Asemi,A.Farajpour,H.R.Asemi,et al.,Influence of initial stress on the vibration of double-piezoelectric-nanoplate systems with various boundary conditions using DQM,Physica E 63(2014)169–179.
[31]A.G.Arani,M.A.Roudbari,S.Amir,NonlocalvibrationofSWBNNTembeddedin bundleofCNTsunderamovingnanoparticle,PhysicaB407(2012)3646–3653.
[32]A.G.Arani,V.Atabakhshian,A.Loghman,et al.,Nonlinear vibration of embedded SWBNNTs based on nonlocal Timoshenko beam theory using DQ method,Physica B 407(2012)2549–2555.
[33]A.G.Arani,S.Amir,A.R.Shajari,et al.,Electro-thermo-mechanical buckling of DWBNNTs embedded in bundle of CNTs using nonlocal piezoelasticity cylindrical shell theory,Compos.Part B-Eng.43(2012)195–203.
[34]A.G.Arani,M.Abdollahian,R.Kolahchi,et al.,Electro-thermo-torsional buckling of an embedded armchair DWBNNT using nonlocal shear deformable shell model,Compos.Part B-Eng.51(2013)291–299.
[35]K.F.Wang,B.L.Wang,The electromechanical coupling behavior of piezoelectric nanowires:Surface and small-scale effects,Europhys.Lett.97(2012) 66005.
[36]L.L.Zhang,J.X.Liu,X.Q.Fang,et al.,Effects of surface piezoelectricity and nonlocal scale on wave propagation in piezoelectric nanoplates,Eur.J.Mech. A Solids 46(2014)22–29.
[37]L.L.Ke,Y.S.Wang,Z.D.Wang,Nonlinear vibration of the piezoelectric nanobeams based on the nonlocal theory,Compos.Struct.94(2012) 2038–2047.
[38]C.Liu,L.L.Ke,Y.S.Wang,et al.,Buckling and post-buckling of size-dependent piezoelectric Timoshenko nanobeams subject to thermo-electro-mechanical loadings,Int.J.Struct.Stab.Dyn.14(2014)1350067.
[39]S.R.Asemi,A.Farajpour,M.Mohammadi,Nonlinear vibration analysis of piezoelectric nanoelectromechanical resonators based on nonlocal elasticity theory,Compos.Struct.116(2014)703–712.
[40]C.Liu,L.L.Ke,Y.S.Wang,et al.,Nonlinear vibration of nonlocal piezoelectric nanoplates,Int.J.Struct.Stab.Dyn.15(8)(2015)1540013.
[41]M.H.Zhao,C.F.Qian,S.W.R.Lee,et al.,Electro-elastic analysis of piezoelectric laminated plates,Compos.Mater.16(2006)63–81.
[42]M.Pietrzakowski,Piezoelectric control of composite plate vibration:Effect of electric potential distribution,Comput.&Structures 86(2008)948–954.
[43]Q.Wang,Axi-symmetric wave propagation in a cylinder coated with a piezoelectric layer,Internat.J.Solids Structures 39(2002)3023–3037.
[44]C.Shu,Differential Quadrature and its Application in Engineering,Springer, London,2002.
[45]C.M.Wang,K.M.Liew,Y.Xiang,et al.,Buckling of rectangular Mindlin plates with internal line supports,Internat.J.Solids Structures 30(1993) 1–17.
[46]K.M.Liew,T.M.Teo,J.B.Han,Three-dimensional static solutions of rectangular plates by variant differential quadrature method,Int.J.Mech.Sci.43(2001) 1611–1628.
[47]T.L.Wu,K.K.Shukla,J.H.Huang,Post-buckling analysis of functionally graded rectangular plates,Compos.Struct.81(2007)1–10.
∗Corresponding author.Fax:+86 10 51682094. E-mail address:llke@bjtu.edu.cn(L.-L.Ke).
http://dx.doi.org/10.1016/j.taml.2016.10.003
2095-0349/©2016 The Author(s).Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
*This article belongs to the Solid Mechanics
 Theoretical & Applied Mechanics Letters2016年6期
Theoretical & Applied Mechanics Letters2016年6期
- Theoretical & Applied Mechanics Letters的其它文章
- Synergy to discovery and innovation—Growth of nanorods
- Numerical simulation of domain switching in multilayer ferroelectric actuators
- Coriolis effect on responses of rotating thin piezoelectric hollow cylinder
- On the role of piezoelectricity in phonon properties and thermal conductivity of GaN nanofilms
- On transition of type V interaction in double-wedge flow with non-equilibrium effects
- Numerical simulation of Gurney flap on SFYT15thick airfoil
