薄壁方钢管再生混凝土短柱屈曲承载力

杨荣华

(1.厦门理工学院 土木工程与建筑学院， 福建 厦门 361024； 2. 华侨大学 土木工程学院， 福建 厦门 361021)

薄壁方钢管再生混凝土短柱屈曲承载力

杨荣华1,2

(1.厦门理工学院 土木工程与建筑学院， 福建 厦门 361024； 2. 华侨大学 土木工程学院， 福建 厦门 361021)

钢管再生混凝土结构是近年来发展起来的一种新型结构形式，薄壁方形钢管再生混凝土构件的钢管壁容易产生局部屈曲而使构件承载力降低，而目前的钢管再生混凝土承载力计算公式中均未考虑局部屈曲的影响。本文在考虑核心混凝土对钢管产生径向力作用并假定非载荷边为弹性约束的情况下，采用能量法对钢管进行屈曲性能分析，并推导出屈曲系数计算公式，再在此基础上采用有效宽度法来考虑薄壁方钢管发生局部屈曲对承载力的影响，从而提出薄壁方钢管再生混凝土轴压短柱承载力计算公式，并用试验数据验证其合理性，研究结果表明：弹性约束系数和钢管的横向力对屈曲系数有一定的影响，当构件截面宽厚比较大时，应当考虑钢管局部屈曲对承载力的降低。

薄壁方钢管； 能量法； 局部屈曲； 有效宽度； 承载力

钢管再生混凝土结构是近年来发展起来的一种新型结构形式，它既继承了钢管混凝土承载力高、延性好等优点，又能够解决克服再生混凝土强度较低、延性较差等缺陷。目前，对这种新型结构的力学性能开展了一系列研究，并取得了一些成果[1～7]。从文献[1～6]所完成的薄壁钢管再生混凝土构件试验来看，当截面宽厚比较大时，钢管再生混凝土在达到极限承载力之前，钢管发生了局部屈曲现象，从而导致钢管再生混凝土构件承载力降低，所以在薄壁方钢管再生混凝土短柱承载力的计算中，考虑局部屈曲造成的不利影响是十分必要的。同时，关于薄壁钢管混凝土柱局部屈曲问题目前已开展了相关的研究，一方面是采用不同方法界定薄壁钢管宽厚比的问题，郭兰慧[8]基于已有的试验研究与理论分析给出了矩形钢管混凝土中钢管不出现局部屈曲时的最大宽厚限值；另一方面是通过设置约束改善钢管屈曲性能的研究，陈勇[9]提出了冷弯设肋与设对拉片的新型薄壁钢管混凝土柱截面形式，蔡健[10]提出设置约束拉杆来提高薄壁构件的屈曲能力。在屈曲理论研究方面，莫时旭[11]、金学锋[12]等对非加载边考虑为弹性约束的矩形板在均匀面内压力作用下的屈曲行为进行了分析，研究表明非加载边考虑为弹性约束更符合实际情况，但在以上研究分析中，弹性约束计算公式计算结果差距较大，同时在分析过程中并未考虑核心混凝土的径向力作用等，与实际不符。本文在考虑核心混凝土的径向力作用并在假定非载荷边为弹性约束的情况下，采用能量法对薄壁方钢管再生混凝土进行屈曲性能分析，并采用有效宽度法来考虑钢管局部屈曲对试件承载力的影响，提出薄壁方钢管再生混凝土中考虑钢管局部屈曲的承载力计算公式，并用试验数据加以验证。

1 薄壁方钢管再生混凝土短柱钢管壁的局部屈曲分析

1.1 模型的建立

用能量法对受压薄壁方钢管柱进行局部屈曲分析，假定管内核心再生混凝土为刚性材料，钢板的两受荷载边为固定支，两非荷载边为可转动弹性约束边，并考虑相邻板件及内填核心再生混凝土对其影响。

取纵向一个半波进行研究[11]，半波长为a，宽为b，由刚性支承板局部屈曲的数学模型可知边界条件为：

(1)

式中：w为位移函数，w≥0；ζ为非荷载边转动的约束刚度。

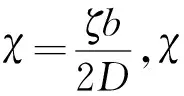
假定沿横向的位移函数为四次泛函且纵向位移函数为一半波余弦函数，在参考文献[10]的基础上，采用满足边界条件的位移函数为：

(2)

式(2)满足上述边界条件，式中C为常数；ψ1、ψ2、ψ3为系数，将式(2)代入式(1)，得到式(2)中的各系数。其具体位移函数为：

(3)

1.2 用能量法对局部屈曲进行分析

根据弹性理论，应用能量法进行小挠度情况下的薄壁钢管屈曲分析。通过分析得到临界屈曲应力的表达式，在以下方程的求解过程由于解析式难以由人工手算获得，通过Matlab软件进行计算求解。

(1)板的弯曲弹性应变能U

(4)

将w代入，得到：

U=

(5)

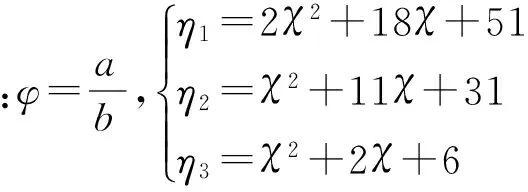
(2)面内均匀荷载所做的功W1

板中面力：Nx=-σxt，Ny=0，Nxy=0

式中：σx为板面应力。

(6)

(3)径向力应变能W2

当构件受压时，核心混凝土与外部钢管同时发生纵向变形，钢管屈曲前核心混凝土向外膨胀对钢板产生横向拉力(忽略剪应力的影响)σy，其计算如下[13]：

σy=∫ζdσx=λσx

(7)

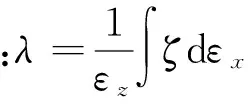
(8)

(4)非加载边弹性约束应变能Uξ

(9)

(5)钢板屈曲总势能Π

Π=U+Uξ+W1+W2

(10)

σxt=

(11)

式中:k为板面的屈曲系数，

(12)

(13)

根据求得的φcr代入公式(12)中，即可得到kcr值，因此，钢板的非载荷边按弹性约束考虑时临界屈曲应力可表述为：

(14)

当不考虑核心混凝土向外膨胀对钢板产生横向力时，λ=0，得到：

(15)

当转动约束刚度ξ→0时，χ→0，此时相当于钢板的非载荷边为简支边，可得φcr= 1.519，kcr=5.467；当ξ→∞时，χ→∞，此时相当于钢板的非载荷边为固定边，φcr= 1.008，kcr=10.311，这与文献[14]用有限条法和文献[15]的半解析有限元法计算结果一致。

1.3 影响因素分析

(1)弹性转动系数的影响

当不考虑横向力作用时，屈曲系数与弹性系数有关。为了研究非加载边弹性转动约束系数对屈曲系数的影响，绘制了λ=0时，k与x的关系曲线，如图1所示，从图中可知：当χ在0～20之间时，屈曲系数k随χ的增加较快，之后增加变缓，最后逐步趋向于10.3左右。

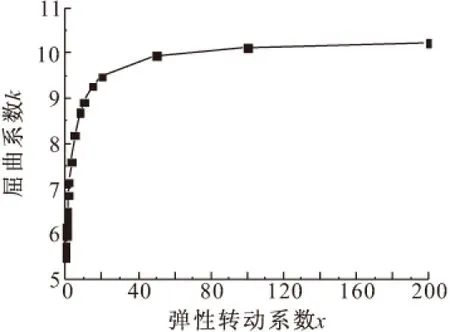
图1 屈曲系数k随约束系数χ变化曲线

(2)横向应力的影响

当给定弹性约束系数时，考虑核心再生混凝土向外膨胀对钢板产生横向力作用的影响，分别分析了当弹性约束系数分别为χ=0，1，2，5，10及∞时，横向拉力的变化情况，如图2所示。从图中可知，当不考虑核心再生混凝土对钢板产生的横向力作用时，对于χ=0情况，屈曲系数为5.67；当χ=∞时，屈曲系数为10.31，与前面推导数值一致。当考虑核心再生混凝土对钢板产生的横向力作用时会导致钢壁屈曲系数减小。核心再生混凝土向外膨胀对钢板产生横向拉力导致钢管壁抵抗局部屈曲能力降低。在计算屈曲系数时，需要考虑其影响。

图2 屈曲系数k随横向约束系数λ的变化曲线

1.4 弹性约束系数χ的确定

文献[16]对箱型截面钢管的板件转动约束系数计算公式进行了推导，但该公式是针对空心钢管的情况，针对内填充核心混凝土的构件其约束系数会提高，根据VonKarman认为的对于面内受压侧边有约束板件达到屈曲后强度，只有在两侧宽度为1/2的地方才产生约束，故对计算壁板相邻约束壁板宽度取其宽度的一半，得到钢板非加载边弹性系数的计算公式如下：

(16)

(17)

(18)

式中：bf、tf分别为计算壁板的宽度和厚度；bw、tw分别为相邻约束壁板的宽度和厚度。当bf=bw，tf=tw时，代入公式(16)得到方形等厚截面的非加载边弹性系数χ=2.1。

1.5 有效宽度计算

有效宽度计算可采用板件有效宽度统一法则[17]，其计算公式如下：

(19)

(20)

(21)

式中：ρ为板件有效宽度折减系数，ρ≤1.0；λ为板件的刚度系数；fy为钢管强度设计值。

2 薄壁方钢管再生混凝土轴压短柱承载力公式

在轴向压力作用下，薄壁方钢管再生混凝土柱的钢管壁易发生局部屈曲而降低了自身的承载力，同时，钢管屈曲后对核心混凝土的约束作用也有所减弱。因此，在计算这类构件的承载力时，应充分考虑到因钢管局部屈曲而造成的不利影响。考虑屈曲作用后的薄壁方钢管再生混凝土短柱承载力公式可采用叠加法进行求解，它等于钢管承载力和核心再生混凝土承载力的叠加。钢管承载力计算时，采用有效宽度法来计算。

薄壁方钢管再生混凝土柱的轴压承载力计算公式如下：

NU=fy·Ase+kcfck·Ac

(23)

式中：Ase=(4be-4t)t；kc为核心再生混凝土强度提高系数，其公式[5]为：kc=1.08+0.15ξ，ξ为钢管再生混凝土的套箍系数，ξ=Asfy/(Acfck)，fck为再生混凝土强度标准值，As为钢管截面积，Ac为核心混凝土面积。

对收集的几组试验数据进行分析计算，先根据泊松比等相关参数计算出横向约束力的大小和临界屈曲应力系数kcr，再根据有效宽度计算法计算其有效宽度，进一步计算其考虑局部屈曲作用的承载力，计算结果如表1所示。

利用国内外典型的设计规程与本文提出的计算公式计算了试件承载力并和文献中给出的试验结果进行对比分析，其比较结果如图3所示，分析结果的统计特征如表2[18～21]所示。从结果上看，本文计算结果与试验结果最为接近，DBJ规程计算结果次之，CECE和ACI规程计算的结果离散性较大，本文给出的考虑构件有效宽度的计算公式较准确地计算了薄壁方钢管再生混凝土轴压短柱的极限承载力。

表1 薄壁方钢管再生混凝土轴压短柱承载力分析

注：Ne为轴压承载力试验值；Nu为轴压承载力计算值。

表2 计算结果与试验结果之比的统计特征

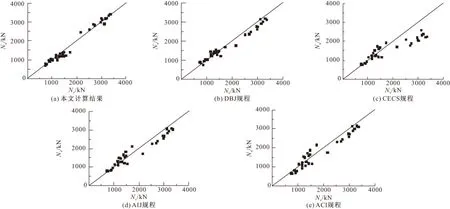
图3 计算结果与试验结果

3 结 论

本文采用能量法并考虑核心混凝土对钢管产生径向力作用和假定非载荷边为弹性约束的情况下，对薄壁方钢管构件的局部屈曲强度公式进行了推导，并在此基础上分析薄壁方钢管再生混凝土轴压短柱在考虑局部屈曲影响的承载力计算公式，并得到以下结论：

(1)在用能量法计算钢管局部屈曲荷载时，弹性约束系数和钢管对核心混凝土的横向力对屈曲系数有一定的影响。弹性转动约束系数增加，屈曲系数也随之增加，而核心混凝土向外膨胀对钢板产生横向拉力导致钢管壁抵抗局部屈曲能力降低。在计算屈曲系数时，需要考虑其影响。

(2)当截面宽厚比较大时，薄壁方钢管再生混凝土钢管容易发生局部屈曲，可采用有效宽度法来考虑局部屈曲对试件承载力的影响，并提出了考虑局部屈曲的薄壁方钢管再生混凝土轴压短柱的承载力计算公式。

(3) 通过对一些试验构件承载力试验值与国内外典型的设计规程和本文提出的公式计算结果进行对比，分析结果表明，本文提出的公式计算值与试验值符合度较高，标准差和变异系数均优于其它公式，从而验证了其的合理性，当构件截面宽厚比较大时，应当考虑钢管局部屈曲对承载力的降低。

[1] 陈宗平, 柯晓军, 陈宇良. 钢管约束再生混凝土柱的变形性能及承载力计算[J]. 应用力学学报, 2014, 31(6): 959-964.

[2] 吴 波, 张金锁, 赵新宇. 薄壁方钢管再生混合短柱轴压性能试验研究[J]. 建筑结构学报, 2012, 33(9): 30-37.

[3] 李佰寿, 张 平, 金爱花, 等. 薄壁方形钢管再生块体混合短柱轴压破坏研究[J]. 建筑材料学报, 2012, 15(4): 451-458.

[4] 杨 俊. 薄壁方钢管-再生混凝土短柱的轴压力学性能研究[D]. 泉州: 华侨大学, 2012.

[5] 潘国锋. 方钢管再生混合混凝土短柱轴压力学性能研究[D]. 泉州: 华侨大学, 2013.

[6] 黄 宏, 孙 微, 陈梦成, 等. 方钢管再生混凝土轴压短柱力学性能试验研究[J]. 建筑结构学报, 2015, 36(s1): 215-221.

[7] 吴 波, 计明明, 赵新宇. 再生混合混凝土及其组合构件的研究现状[J]. 工程力学, 2016, 33(1): 1-10.

[8] Guo L, Zhang S, Kim W J, et al. Behavior of square hollow steel tubes and steel tubes filled with concrete[J]. Thin-Walled Structures, 2007, 45(12): 961-973.

[9] 陈 勇, 董志峰, 张耀春. 方形薄壁钢管混凝土轴压短柱约束模型的建立[J]. 工程力学, 2012, 29(9): 157-165.

[10]蔡 健, 何振强, 金雪峰. 带约束拉杆方形钢管混凝土轴压柱局部屈曲性能[J]. 工程力学, 2007, 24(5): 169-175.

[11]莫时旭, 钟新谷, 赵人达. 刚性基底上弹性约束矩形板的屈曲行为分析[J]. 工程力学, 2005, 22(2): 174-178.

[12]金雪峰, 张学文, 蔡 健. 方形钢管混凝土轴压柱局部屈曲性能的研究[J]. 合肥工业大学学报(自然科学版), 2007, 30(7): 885-887.

[13]曹宝珠, 张耀春. 方形薄壁方钢管混凝土柱管壁的宽厚比限值[J], 哈尔滨工业大学学报, 2004, 36(12): 1713-1716.

[14]杨晓冰. 矩形钢管混凝土柱局部屈曲性能研究[D]. 西安: 西安建筑科技大学, 2002.

[15]Uy B, Bradford M A. Elastic local buckling of steel plates in composite steel-concrete members[J]. Engineering Structures, 1996, 18(3): 193-200.

[16]F 柏拉希. 金属结构的屈曲强度[M]. 同济大学钢木教研室， 译. 北京: 科学出版社, 1985.

[17]Peköz T. Development of a Unified Approach to the Design of Cold-formed Steel Members[R]. AISI,1986.

[18]DBJ 13-51-2003, 钢管混凝土结构技术规程[S].

[19]CECS 159-2004. 矩形钢管混凝土结构技术规程[S].

[20]AIJ-1997, Recommendations for Design and Construction of Concrete Filled Steel Tubular Structures[S].

[21]ACI 318-08, Building Code Requirements for Structural Concrete and Commentary[S].

Buckling Bearing Capacity of Recycled Concrete-filled Thin Walled Square Short Steel Tube

YANGRong-hua1,2

(1.School of Civil Engineering and Architecture, Xiamen University of Technology, Xiamen 361024, China; 2.Collge of Civil Engineering, Huaqiao University, Xiamen 361021, China)

Recycled concrete-filled steel tube is a new type of structure which has been developed in recent years. For recycled concrete-filled thin-walled square steel tube member, the steel tube wall is prone to local buckling and the bearing capacity of the member is reduced. But the effect of local buckling of the member is not considered in the calculation formula of bearing capacity. In this paper, it assumed that the steel plate is subjected to spring constrain at the unloading edge and the radial force of the core concrete is considered, the buckling behavior of steel tube is studied by using energy method and the calculation formula of buckling coefficient is derived. Based on the effective width method, the effect of local buckling on the bearing capacity of the thin-walled square steel tube is considered. The calculation formula for the bearing capacity of the recycled concrete-filled steel tube axial compression stub column is put forward, and the rationality of the formula is verified by the experimental data. The results show that the elastic constraint coefficient and the lateral force of the steel tube have a certain influence on the buckling coefficient. When the section width thickness is relatively large, the local buckling of the steel tube should be considered.

thin walled square steel tube; energy approach; local buckling; effective width; bearing capacity

2016-02-18

2016-05-30

杨荣华(1979-)，女，湖南岳阳人，讲师，硕士，研究方向为钢与混凝土组合结构及施工管理(Email:rhyang@xmut.edu.cn)

国家自然科学基金(51478404)；福建省中青年教师教育科研项目(JA15380)

TU398+.9

A

2095-0985(2016)06-0057-06