基于有限元强度折减法对齿墙在软基上闸室稳定的影响研究

周演腾，丁贯西，许 淼

1.绍兴水利局，浙江 绍兴 312000；2.绍兴市河道管理委员会办公室，浙江 绍兴 312000)

基于有限元强度折减法对齿墙在软基上闸室稳定的影响研究

周演腾1,2，丁贯西1，许 淼1

1.绍兴水利局，浙江 绍兴 312000；2.绍兴市河道管理委员会办公室，浙江 绍兴 312000)

水闸地基的不稳定性，对闸室的抗滑稳定造成众多不利因素，而水闸中常用起防冲抗滑作用就是齿墙，因此有必要对齿墙在软基上的闸室稳定的影响进行分析.针对该问题，采用有限元强度折减法来研究齿墙在软基上闸室稳定的影响，并根据5种不同情况对水闸进行有限元分析计算结果，结果表明齿墙深度的增加能提高闸室的抗滑稳定安全系数.

闸室;有限元强度折减法;齿墙;稳定系数

0 引 言

水闸在我国有着广泛的应用，其地基条件亦是多种多样的.水闸地基宜取完整新鲜的岩石，但我国水闸多建设在河流下游的平原和滨海地区，水闸闸基以松软的土基为多，中等强度的砂砾石地基在工程中也较为常见.软土地基的承载能力有限，而砂砾石地基的抗渗性不好，工程中对它们都要进行相应的处理[1]，以达到稳定的要求.

《水闸设计规范SL265—2001》仅从其对闸室沿地基表层抗滑稳定性的增强作用来考虑，没有给出具体的齿墙设计依据.但从其抗滑机理上，可利用土体稳定基本理论进行分析[2-4].而有限元法常用于土坡的稳定性分析，其主要方法有：①应力水平法；②搜索滑面法；③滑面应力法；④强度折减法.笔者现针对不同齿墙设置情况下的闸室结构进行有限元分析，根据模拟的结果分析研究齿墙对闸室滑动形态的影响.在计算中为了使问题得到简化，以突出齿墙对闸室滑动的影响，假设地基为均质地基.

1 闸室稳定分析的有限元法

1.1 有限元强度折减法简介

有限元强度折减法的要点就是在外荷载不变的情况下，利用c′=c/R和φ′=arctan(tanφ/R)来逐渐降低地基土体材料的强度指标c、φ，然后对结构进行弹塑性有限单元计算，直到土基达到临界破坏，此时的材料折减系数R就是结构的抗滑稳定安全系数Fs.

有限元的基础是有限元网格的划分和材料本构模型的选取，合理的网格划分不仅可以有效的分析问题，并且可以降低对计算机配置的要求，因此在计算中要选取适当的单元类型.

材料本构模型的选取对模拟结果的准确性有很大影响，要根据材料的性质选用适当的本构模型.随着有限元技术的发展和工程实际的深入，现在已有多种本构模型备选用，这些模型多数经过了大量工程应用的检验.

边界条件的选取对计算结果同样具有较大的影响，工程实际中计算分析的边界条件通常较为复杂，对它的选用存在较大的近似性，应根据不同的工程实际合理地选用边界条件.当结构的形状和荷载具有某种对称性时，往往选取结构的一部分来进行计算，这时在对称面或对称轴上的边界条件应根据具体的情况分别予以确定.

控制闸室稳定的荷载主要包括水荷载和结构自重.在这些荷载的作用下，地基土要发生塑性变形，当这个塑性区形成一个连续的面时，这个面就是我们要找的潜在滑动面.由于分析重点是地基土在各种力作用下的综合反映，因此混凝土的本构模型也可以采用较为简单的弹性模型，这样可以加快计算的速度.

1.2 材料模型选取

计算中，土体材料的破坏准则采用莫尔—库仑破坏准则，莫尔—库仑准则假定破坏发生时，材料任意一点的剪应力达到一定的值，该值与同一平面上的正应力成线性的关系，可用莫尔应力圆表示(见图1).

图1 摩尔应力圆

莫尔—库伦模型的定义如下：

τ=c-σtanφ

(1)

从应力圆可以看出：τ=scosφ，σ=σm+ssinφ，把它们代入式(1)并进行计算得：

s+σmsinφ-ccosφ=0

(2)

一般的应力状态可便捷的写成：

F=Rmcq-ptanφ-c=0

(3)

纵向应力和偏应力平面上的莫尔库伦屈服面的形状(见图2),图2中Rmc和Θ的定义和图1中的相同.

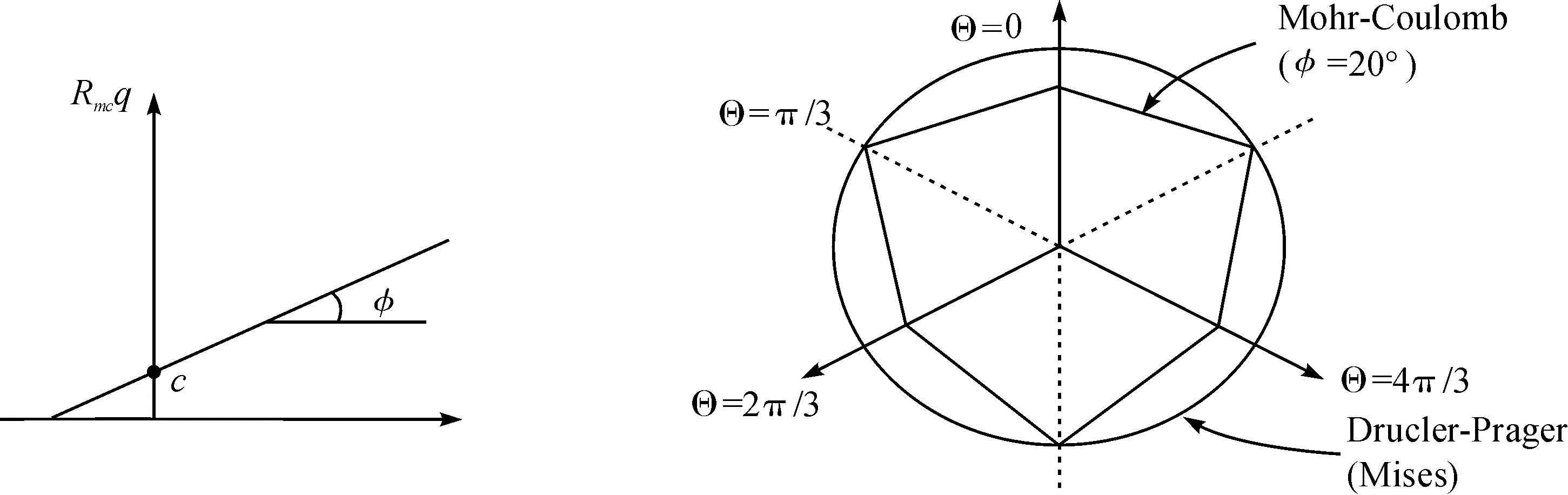
图2 纵向应力和偏应力平面上的莫尔库伦屈服面

2 实例分析

某节制闸总宽度576 m，36闸，每闸净宽16.0 m，中墩厚2.0 m，闸轴线垂直两岸大堤，底板为开敞式钢筋混凝土.闸室顺水流方向的长度27.50 m，闸室垂直水流方向总长度646.0 m[7].

在本次计算中，土体材料采用弹塑性模型，利用Mohr-Coulomb破坏准则进行分析，而齿墙则采用弹性模型，具体参数(见表1).

表1 有限元计算的材料参数

地基土混凝土密度/(kg/m3)1800密度/(kg/m3)2450弹性模量/Pa8.0×107弹性模量/Pa3.0×1010泊松比0.3泊松比0.2摩擦角/(°)30屈服应力/Pa2.0×105

荷载施加的过程建立多个分析步来实现.不同的分析步，按照实际工程中荷载的加载顺序分别施加到结构中去.而在初始步中只施加边界条件，在后续的分析步中再陆续施加其它荷载的作用，计算中只对模型施加水压力和结构自重，作用于水闸上的偶然荷载则不予计算.

本模型共有5 231个节点，5 002个单元，其中主要以四节点减缩平面应变单元为主，局部以三节点平面应变单元过渡.

闸室是否发生滑动破坏的判定标准主要根据有限元计算的收敛与否确定闸室是否发生滑动破坏，当计算收敛时则认为闸室处于稳定状态；当计算不收敛时则可判定结构发生了破坏.通过分析地基塑性应变的变化和分布来判断地基是否处于稳定状态，如果当地基内某一幅值的塑性应变区域相通时，则可判断地基发生破坏.根据计算所得的域内某一部位的位移与折减系数之间的关系变化特征来确定失稳状态.Zienkiewice最早采用最大的节点位移作为结构失稳的依据，当位移急剧增加时即认为水闸发生失稳破坏.图3为不设齿墙时闸室最大节点位移值与强度折减系数的关系曲线.

图3 无齿墙时的折减系数与最大位移曲线图

在本文中认为当地基内特定区域某一幅值的塑性连成一片时，闸室发生失稳破坏.在正常挡水位情况下，分析齿墙对闸室滑动的影响，在设置一个齿墙情况下进行分析，通过有限元计算得到它们的等效塑性应变图，通过图形的观察得出齿墙的设置对闸室滑动的影响.

单个齿墙的设置深度及其对应的塑性区(见图4～图8).

图4 无齿墙时的塑性变形区

图5 齿墙深0.5 m时的塑性变形区

图6 齿墙深1.0 m时的塑性变形区

图8 设置单个2 m齿墙时闸基塑性变形区

通过对图4～图8的观察可知，当设置单个齿墙时，结构的滑动面位于闸底板轮廓附近，在闸室的上、下游端将形成较大的塑性区.图4～图8还表明随着齿墙深度的加大，当闸室结构发生破坏时，滑动体的体积增加了，这样抗滑力将得到提高，通过与图3对比可以得出随着齿墙深度的增加，闸室的抗滑稳定安全系数得到了提高.

3 结 语

为更好的研究齿墙对软基上闸室稳定的影响程度，采用有限元强度折减法，结果表明齿墙深度的增加能提高闸室的抗滑稳定安全系数.本文仅在一种软土地基中进行齿墙对闸室稳定性的影响研究，而不同土质和不同形状的齿墙均对结构的力学性能有较大影响.因此可以考虑在不同土质的情况下，设置不同形状的齿墙对提高稳定性的程度做进一步的研究.

[1] 裘华锋.汇潭前方闸地基处理方案的分析[J].浙江水利水电学院学报,2014,26(3):45-47.

[2] 屠毓敏,俞亚南.齿坎式护岸结构抗滑稳定性分析[J].土木工程学报,2000,33(5):97-99.

[3] 王 千,荆 凯,王 建.齿墙对提高水闸抗滑作用的分析[J].水力发电,2013,39(5):41-45.

[4] 屠毓敏,吉建兴.软粘土地基中齿坎抗滑效应的研究[J].岩石力学与工程学报,2003,22(1):159-161.

[5] 陈倩倩.基于强度折减有限元法的边坡失稳判据研究[D].西安:长安大学,2015.

[6] UGAI K. Amethodof Calculation of Totalsafety Factor of Slopes by Elastic-plasticFEM[J].Soil and Foundations,1989,29(2):190-195.

[7] 郭永军.刘家道口枢纽工程闸墩模板设计浅谈[J].四川水利,2008,11(1):132-135.

Impact of Key-wall on Chamber Stability Coefficient Based on Strength Reduction Method

ZHOU Yan-teng1, 2, DING Guan-xi1, XU Miao1

(1.Shaoxing Water Conservancy Bureau, Shaoxing 312000, China;2.Shaoxing River Management Office, Shaoxing 312000, China)

Due to the rapid development of water conservancy, a lot of sluices have been built on soft ground. Many negative factors of anti-sliding stability are caused by the foundation of the chamber instability, and the key-walls play a role in chamber stability coefficient, which is worth detailed study and analysis. The impact of the key-wall on the chamber stability coefficient is analyzed by using finite element shear strength reduction method. According to the FEM computation for chamber with five different situations, that the stability coefficient increases along with the increase of the key-wall depth can be found out.

chamber; finite element shear strength reduction method; key-wall; stability coefficient

2016-04-08

周演腾(1983-)，男，浙江台州人，工程师，从事水利工程管理.

TV662

A

1008-536X(2016)08-0024-04