一种战车主减速器温度预测方法研究
(中国人民解放军91980部队,山东 烟台 264000;2.海军航空工程学院,山东 烟台 264001)
环境适应性设计与分析
一种战车主减速器温度预测方法研究
李田科1,沙卫晓1,李伟1,于仕财2
(中国人民解放军91980部队,山东 烟台 264000;2.海军航空工程学院,山东 烟台 264001)
目的针对战车主减速器温度预测需求,建立时间序列ARIMA多步预测和BP神经网络预测模型,提出基于BP神经网络修正误差的ARIMA模型温度预测方法。方法结合BP神经网络的非线性能力与ARIMA模型预测能力,分析ARIMA在多步预测时误差产生原因,在神经网络对ARIMA多步误差进行预测基础上计算修正因子,把误差修正因子和BP网络结合,实现对多步预测误差的修正。结果ARIMA模型多步预测时,预测误差随预测步数的逐步增加不断增大,引入了误差修正因子进行修正。通过预测值与实际值进行对比,可有效提高预测准确度。结论BP神经网络和误差修正因子结合应用可显著提高温度预测效果。
误差修正因子;温度预测;ARIMA模型;BP神经网络
战车在编队机动行军时,主减速器等部位温度 不得超过140 ℃,否则需停车采取降温措施,防止温度过高导致事故。行军中需反复停车用红外测温仪检查各部位温度,耗费大量时间,导致贻误战机。对各部位加装温度传感器,采集各部位数据,并结合以往历史温度数据进行综合处理,采用智能推理算法给出精确温度预测值,既可避免多次停车检查温度,又可充分发挥底盘的使用效能[1—2]。
主减速器等温度有明显运行时间相关性,故采用时间序列分析法[3—5]。用ARIMA时间序列模型,结合BP神经网络的非线性能力,以BP神经网络对ARIMA模型误差预测为基础,利用误差修正因子实现多步预测误差修正,以提高温度预测精度。
1 基于ARIMA模型的温度预测[6—10]
1.1 数据分析及预处理
主减速器等部位温度除受自身因素影响外,还受速度、路况、环境温度等影响。温度数据变化规律包含其他影响因素。温度序列纵向变化是数据间关系及变化规律,并把规律延续到预测期。表1中数据是主减速器温度实测数据,车速为50 km/h,时间为4月份,温度数据总量为56,时间间隔为1 min。

表1 主减速器温度数据Table 1 Temperature data of Main Reducer
表1中的56组数据,前50组数据用于建立预测模型,后6组数据用作检验数据,检验模型的预测效果。
温度数据的偏自相关函数可以认为是截尾的,但自相关函数呈现缓慢衰减的趋势,序列是非平稳序列。经两次差分处理后,温度时间序列转变成平稳序列,则ARIMA(p,d,q)模型中可以确定d值为2。
1.2 模型识别与参数估计
二阶差分后的自相关与偏自相关函数都是拖尾的,则差分后模型确定为ARMA(p,q),其中p和q值从p=1,q=1开始逐渐增加,即模型为ARIMA(p,2,q)。根据不同的p和q值,得到残差方差估计值,见表2。

表2 残差方差Table 2 Residual variance
由表2可初步判断模型为ARIMA(3,2,3)。
1.3 模型的检验
主要进行模型的显著性检验,即对残差序列进行是否为白噪声的检验。根据模型检验方法,分别作出残差序列的自相关与偏自相关函数图,可知自相关和偏自相关函数都在界限内,不显著超界。由此判断残差为白噪声序列,所选模型有效。
1.4 主减速器等温度的预测
最终经过检验有效的 ARIMA(3,2,3)模型表达式为:

对主减速器等温度进行预测,向前预测5步,共预测2次,预测结果与实际数据如图1所示。

图1 ARIMA模型预测结果Fig.1 Prediction results of ARIMA model
预测值与实际值相对误差最大为1.16%。预测的平均绝对误差随着预测步长增加有增大趋势,预测算法存在缺陷。
2 ARIMA模型误差修正[11]
随着预测步数增加,ARIMA模型预测无法解决预测误差不断增大的问题。通过BP神经网络模型对ARIMA模型误差预测,用误差修正因子对多步预测误差修正,得到多步预测结果,预测原理示意如图2所示。

图2 误差修正原理Fig.2 Schematic diagram of error correction principle
预测的误差为:

根据线性最小方差预测原理可知,以t为原点,向前l期的预测值 ()ˆtXl是tlX+的条件期望值tlX+。根据条件期望的基本性质,可得ARMA(p,q)预测公式。条件期望为:

式(2)说明条件期望运算的线性性质。式(3)表明对未来时间观测值进行预测的结果即预测值,就是其条件期望,过去和现在的观测值就是其本身的条件期望。式(4)表明过去和现在的误差是其本身的条件期望,未来误差的条件期望是0。
利用条件期望的上述性质,得到一步预测公式:

二步预测公式为:
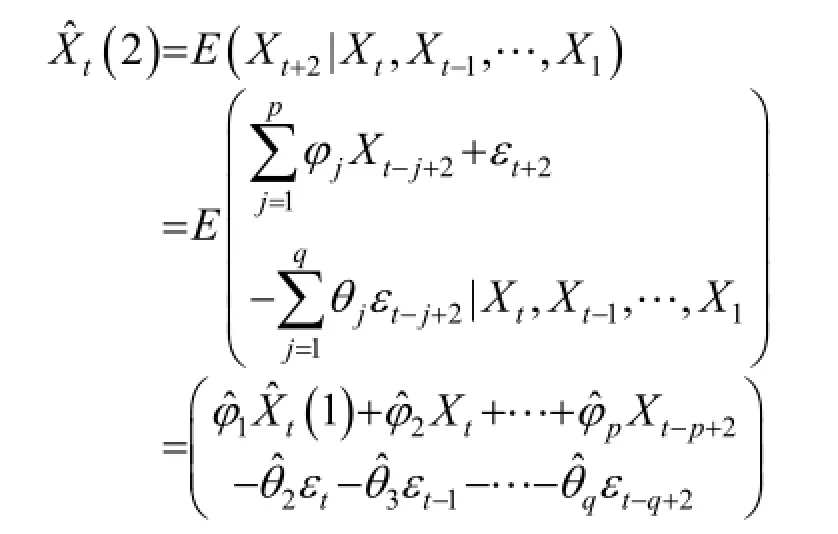
第l步预测公式为:

当l>p,l>q时,式(5)变为:

由式(6)可知,t时刻的第l步预测值,是前l-1步预测值的线性回归,则第l步预测误差累计了前l-p步预测误差,函数关系为:

引入误差修正因子δt(l),表达式为:

以误差修正因子δt(l)的值代替误差值et(l),结合式(1),则最终的预测结果变为:

3 BP神经网络误差预测模型[12—14]
3.1 模型结构的确定
1)输入、输出节点数。用 BP网络预测模型进行误差预测,其输入为ARIMA模型残差值,输出为相应误差预测值。根据 ARIMA(3,2,3)模型,确定输入层的节点数为8个,输出层节点数为1个。
2)隐层节点数、层数。隐含层的层数确定为1,隐含层节点数选择区间为[3,17],以训练样本为输入,选择不同的节点数,以输出误差接近平稳为原则,选取最终的节点数。最终确定隐含层的节点数目为8个,用于误差预测的神经网络模型结构为8-8-1。
3.2 样本选取
神经网络的输入为 ARIMA(3,2,3)模型的残差值,残差数据见表3。

表3 ARIMA(3,2,3)模型预测的残差Table 3 Prediction residual of ARIMA(3,2,3) model
4 修正误差的ARIMA模型预测
4.1 网络的训练
ARIMA(3,2,3)模型的残差数据的总量为 48,BP网络结构为8-8-1,则用于训练的数据共分为40组,即40×8的矩阵。
用 MTALAB神经网络工具箱进行模型的训练[15],学习算法为L-M算法,训练函数为trainlm,输入层与隐含层间的激励函数为tansig函数,隐含层与输出层之间的激励函数为 purelin函数,目标函数为MSE,训练次数设为1000次,最大失败次数为6次,目标函数的收敛误差为le-5,训练的时间及其他参数为缺省值。
4.2 BP网络预测
利用训练好的BP网络对ARIMA的误差进行预测,以迭代方式进行,即以预测出的误差值作为下一步预测的输入,预测结果见表4。

表4 BP网络误差预测结果Table 4 Prediction results of BP network error
从l≥3开始计算误差修正因子,见表5。

表5 误差修正因子Table 5 Error correction factors
将BP网络模型预测的误差,以及通过计算得到的误差修正因子的值,与ARIMA的多步预测值相加,得到的预测结果见表6。

表6 预测结果Tab.6 Prediction results
4.3 预测结果分析
ARIMA模型预测、BP神经网络直接预测和BP神经网络与 ARIMA模型组合预测对比如图 3所示。

图3 温度预测值对比Fig.3 Contrast diagram of temperature predictive value
BP神经网络与 ARIMA模型组合预测精度,明显高于单一模型的预测精度。利用修正因子进行误差修正的预测方法,在多步预测时,平均绝对误差相对 BP网络误差预测方法的平均绝对误差较小,预测效果较好。BP网络误差预测方法与利用修正因子的预测方法都能改善ARIMA模型的预测效果,提高预测的准确度,但利用修正因子的预测效果更好。
5 结语
从上面的预测值对比可以看出,文中提出基于BP神经网络修正误差的ARIMA模型预测的方法具有很好的预测效果。依据温度序列的时间相关性、非平稳性、不确定性和非线性特点,建立时间序列ARIMA多步预测模型和BP神经网络时序预测模型,分析ARIMA在多步预测时误差产生原因,以误差修正因子和BP网络相结合的方法,在神经网络对ARIMA多步误差进行预测基础上计算修正因子,修正ARIMA多步预测值。结果表明,该方法提高了预测精度,优于直接利用神经网络误差预测进行修正的方法,是实现温度预测的新方法,具有较高的应用价值。
[1] 许翔, 刘瑞林, 董素荣. 轮式车辆高原环境适应性评价研究[J]. 装备环境工程, 2014, 11(4): 82—87. XU Xiang, LIU Rui-lin, DONG Su-rong. PHM Technique Studies and Engineering Applications Faced to Missile Storage and Life Extension[J]. Equipment Environmental Engineering, 2014, 11(4): 82—87.
[2] 马凌, 李俊, 赵韶平. 面向导弹贮存延寿的 PHM 技术研究与工程应用[J]. 装备环境工程, 2014, 11(4): 42—48. MA Ling, LI Jun, ZHAO Shao-ping. PHM Technique Studies and Engineering Applications Faced to Missile Storage and Life Extension[J]. Equipment Environmental Engineering, 2014, 11(4): 42—48.
[3] 范涛涛, 寇艳廷, 刘晨, 等. 时间序列分析中数据的平稳性判定研究[J]. 现代电子技术, 2013, 36(1): 66—68. FAN Tao-tao, KOU Yan-ting, LIU Chen, et al. Judgement of Data Stability in Time Sequence Analysis[J]. Modern Electronic Technique, 2013, 36(1): 66—68.
[4] 邱敦国, 杨红雨. 一种基于双周期时间序列的短时交通流预测算法[J]. 四川大学学报(工程科学版), 2013, 45(5): 64—68. QIU Dun-guo, YANG Hong-yu. A Short-term Traffic Flow Forecast Algorithm Based on Double Seasonal Time Series[J]. Journal of Sichuan University (Engineering Science Edition), 2013, 45(5): 64—68.
[5] 岳继光, 杨臻明, 孙强. 区间时间序列的混合预测模型[J]. 控制与决策, 2013, 28(12): 1915—1920. YUE Ji-guang, YANG Zhen-ming, SUN Qiang. Hybrid Model for Interval-valued Time Series[J]. Control and Decision, 2013, 28(12): 1915—1920.
[6] 甘旭升, 端木京顺, 高建国. 基于 ARIMA模型的航空装备事故时序预测[J]. 中国安全科学学报, 2012, 22(3): 97—102. GAN Xu-sheng, DUANMU Jing-shun, GAO Jian-guo. Time Series Prediction of Aviation Equipment Accident Based on ARIMA Model[J]. Control and Decision, 2012, 22(3): 97—102.
[7] 孙冬梅, 陈玲, 朱靳. 基于 ARIMA模型误差修正的小波神经网络风速短期预测[J]. 计算机与应用化学, 2013, 30(3): 322—326. SUN Dong-mei, CHEN Ling, ZHU Jin. Short-term Forecasting of Wind Speed Based on Wavelet Neural Network and ARIMA Model of Error Correct[J]. Computers And Applied Chemistry, 2013, 30(3): 322—326
[8] YAN Bing-ji, ZHANG Jian-liang, GUO Hong-wei. High-temperature Performance Prediction of Iron Ore Fines and the Ore-blending Programming Problem in Sintering[J]. International Journal of Minerals, Metallurgy and Materials, 2014, (8): 741—747.
[9] ANAND K S, EKATA D. Applicability of Box Jenkins ARIMA Model in Crime Forecasting: A case study of counterfeiting in Gujarat State[J]. International Journal ofAdvanced Research in Computer Engineering & Technology, 2013, 1(4): 494—497.
[10] 郭赞洪, 唐其环. GM(1,1)正弦模型修补气温监测缺失数据的探讨[J]. 装备环境工程, 2015, 12(1): 25—30. GUO Zan-hong, TANG Qi-huan. Exploration of Repairing Temperature Monitoring Patch Missing Data with GM (1,1) Sinusoidal Model[J]. Equipment Environmental Engineering, 2015, 12(1): 25—30.
[11] CLIFFORD D. Correction Factors for Unbiased, Efficient Estimation and Prediction of Biomass from Log-Log Allometric Models[J]. Forest Ecology and Management, 2013, 310: 375—381
[12] 可荣博, 王铁宁, 宋宁波. 基于遗传 BP神经网络的装甲装备器材需求预测[J]. 火力与指挥控制, 2015, 40(6): 99—104. KE Rong-bo, WANG Tie-ning, SONG Ning-bo. Research on Armored Equipment Demand Forecasting Based on BP Neural Network[J]. Fire Control & Command Control, 2015, 40(6): 99—104.
[13] DENG Ai-dong, ZHAO Li, XIN Wei. Application of Quantum Neural Networks in Localization of Acoustic Emission[J]. Journal of Systems Engineering and Electronics, 2011, 22(3): 507—512.
[14] WANG Ying, LU Cui-jie, ZUO Cui-ping. Coal Mine Safety Production Forewarning Based on Improved BP Neural Network[J]. Lnternational Journal of Mining Science and Technology, 2015, 25(2): 319—324.
[15] 陈立伟, 谭志良, 崔立东. 改进的LMS算法在Simulink仿真平台实现[J]. 装备环境工程, 2015, 12(6): 26—30. CHEN Li-wei, TAN Zhi-liang, CUI Li-dong. Realization of LMS Algorithm on Simulink Simulation Platform[J]. Equipment Environmental Engineering, 2015, 12(6): 26—30.
Research on Temperature Prediction Method of Main Reducer for Chariot
LI Tian-ke1,SHA Wei-xiao1,LI Wei1,YU Shi-cai2
(1.PLA, No.91980 Troop, Yantai 26400, China; 2.Naval Aeronautical & Astronautical University, Yantai 264001, China)
ObjectiveTo establish models for time series ARIMA multistep prediction and BP neural network prediction as required by temperature prediction of main reducer for chariot and propose methods for temperature prediction of ARIMA model based on BP neural network error correcting.MethodsNonlinear ability of BP neural network and prediction ability of ARIMA model were combined to analyze causes of error in multistep prediction of ARIMA. Correction factors were calculated based on ARIMA multistep error prediction of neural network. Error correction factors and BP neural network were combined to achieve correction of error correction factors.ResultsThe prediction error increased with prediction steps in multistep prediction of ARIMA model. Error correction factors were used for correction. Comparison of prediction values and actual values improved the prediction accuracy effectively.ConclusionCombined application of BP neural network and error correction factors can improve the temperature prediction result effectively.
error correction factors; temperature prediction; ARIMA model; BP neural network
10.7643/ issn.1672-9242.2016.06.007
TJ812+.6
A
1672-9242(2016)06-0035-06
2016-06-16;
2016-07-03
Received:2016-06-16;Revised:2016-07-03
国家自然科学基金(61179017)
Fund:Suported by the " Natural Science Foundation of China "(61179017)
李田科(1976—),男,山东烟台人,硕士,高级工程师,主要研究方向为导弹装备维修与保障等。
Biography:LI Tian-ke(1976—), Male, from Yantai, Shandong, Master, Senior engineer, Research focus: missile equipment maintenance support.

