在比较中发展学生思维

福建省长汀县童坊中心学校 陈春荣

在比较中发展学生思维

福建省长汀县童坊中心学校 陈春荣

课堂教学是发展学生思维的过程，思维能力的发展需要长期的培养和训练。教学中引导学生把“旧知”与“新知”进行比较，找到新旧之间的联系和区别，学生思维得到充分发挥，加深了对知识的理解，有利于牢固掌握新知。发展思维、培养能力是数学教学永恒的主题，在小学数学教学中，要重视比较法的运用。

一、比较条件与问题，培养思维的准确性

比较是学生各种认识和各种思维的基础。有比较才有辨别，因此，在教学中对只有一句之差、一字之别的相关习题，教师要让学生在比较、鉴别中分析已知条件与问题，找出它们的内在联系，使学生能全面、准确地思考问题。例如：

（1）甲块地6.4公顷，比乙块地的4倍多1.6公顷，乙块地有多少公顷？

（2）甲块地6.4公顷，乙块地比甲块地的4倍多1.6公顷，乙块地有多少公顷？

这一组题目很容易弄错，粗看相似，其实相差很远。解题时，先让学生观察比较，再引导发现相同点：一个已知条件相同（甲块地6.4公顷）；问题相同（求乙块地有多少公顷）。不同点：第（1）题是“甲块地比乙块地的4倍多1.6公顷”，第（2）题是“乙块地比甲块地的4倍多1.6公顷”。然后让学生抓住比较的关键句，讨论得出：第（1）题是“乙块地的面积”作“1倍数”，第（2）题是“甲块地的面积”作“1倍数”，从而确定解答这两道应用题要使用不同的方法。通过这种条件与问题的比较，不仅可以使学生很准确完整地理解题意，促进学生思维的发展，还能使学生找到解决问题的关键。

二、比较解题思路，培养思维的概括性

人们把同一类事物的共同特征或多种事物间的同一类联系找出来并加以概括，用来反映整个类别的事物或事物间的联系，这就是比较的好处，很显然，这种异中求同的思维方法，只有通过比较才能实现。如：

（1）渔业队五月份捕鱼2400吨，六月份捕的是五月份的125%，六月份捕鱼多少吨？

（2）渔业队五月份捕鱼2400吨，六月份比五月份多捕了25%，六月份比五月份多捕了多少吨？

（3）渔业队五月份捕鱼2400吨，六月份比五月份多捕了25%，六月份捕了多少吨？

这组题目粗看各不相同，先让学生解题，再比较解题方法，学生容易发现：三道题解题思路相同，都是求一个数的百分之几是多少。按照这个思路，学生明白，求一个数的百分之几是多少时，应先确定单位“1”是否已知，发现三道题的单位“1”都是已知的（2400吨），要用乘法来解答。

三、比较画图方法，培养思维的灵活性

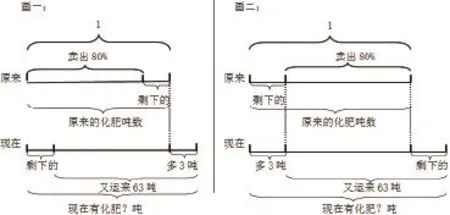
实践证明：动手能促进儿童的思维发展。可见动作与思维是密不可分的。在教学中学生经常会遇到一些数量关系比较抽象的题目，要解决数学问题的抽象和学生思维的形象这一矛盾，用线段图来表示，可以帮助学生理解题目的意思，更快掌握解题思路，培养学生灵活的思维。例如教学《百分数应用题》 ：某商店有一批化肥，卖出80%后，又运来63吨，这时仓库里的化肥比原来还多3吨，现在仓库里有化肥多少吨？

通过比较两种线段图，发现画法一中百分率“80%” 对应的具体量不明显，而画法二不依常规，寻求变异（“卖出80%”画在后面，剩下的吨数画在前面），这样就把题中的数量关系直观、形象地展示出来：(63+3)与80%相对应，学生很容易就列出算式：（63-3）÷80%+3。由此可见，用比较方法训练学生思维，可以真正起到化难为易的效果，它使学生思维灵活，思路开阔，探索能力得到提高。

四、比较计算方法，培养思维的敏捷性

在计算时，要引导学生根据具体情况进行简便计算或选择合理算法，有利于培养学生思维的敏捷性。因此，教师要指导学生运用简便运算的法则、定律、性质进行速算练习，在计算中发现简算的方法，积累经验，培养学生正确、灵活的计算技巧。如：计算2.11-0.53+0.89-1.47，学生一般会出现两种算法：

针对以上情况，教师要延迟评价。让学生观察数字，哪两个数之间有联系？有怎样的联系？并比较这两种算法，发现解法二运用凑整数的方法来计算，2.11与0.89先相加得3，0.53与1.47的和也正好是整数2，再根据减法的运算性质计算结果。通过简便计算训练，使学生知道利用已有的知识体系和数学经验来思考，找到解决问题的技巧。

五、比较概念内涵，培养思维的深刻性

知识的应用就是信息的识别、提取和加工的过程。学生在解决问题时，首先识别信息属于哪一类（即类化），然后以此为索引，在记忆中提取相应的思维策略。在知识的应用过程中，学生对信息识别常会错乱混淆，教师应对概念的内涵进行比较。

如教学《长（正）方形的周长与面积计算》时，对于初学者，周长易算成面积；面积易算成了周长。对于一些易混易错的概念，主要原因是对意义的理解不够，只停留在记住概念和对定义的表述上，没有真正把握周长与面积这两个概念的本质意义。教学时利用直观的图例，让学生在比较中发现求周长和面积的不同。

（1）周长

（2）面积：

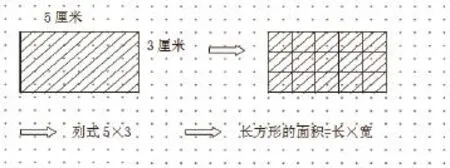
通过对比，发现长方形的周长是围成长方形的四条边长的和（5+3+3+5），图（1）把周长分成两部分，所以长方形的周长=长×2+宽×2=（长+宽）×2。而长方形的面积是指围成长方形的面的大小，用边长为1厘米的小正方形去摆，一行摆5个，一共摆3行，图（2）的面积就是15平方厘米。15平方厘米正好是长与宽的乘积，所以长方形的面积=长×宽。教学时应让学生动手量一量、摆一摆、算一算。通过动手操作突破难点，让他们在操作中发现方法，正确区分。