Group Lasso正则化问题的邻近梯度算法的线性收敛性

晁绵涛，邓 钊，唐春明

(广西大学数学与信息科学学院， 广西高校数学及其应用重点实验室， 广西南宁530004)

Group Lasso正则化问题的邻近梯度算法的线性收敛性

晁绵涛，邓 钊，唐春明

(广西大学数学与信息科学学院， 广西高校数学及其应用重点实验室， 广西南宁530004)

研究一类目标函数是光滑凸函数与Group Lasso正则项和的优化问题。利用不动点迭代理论分析了邻近梯度算法的全局收敛性和有限收敛性。特别地，在不要求光滑凸函数为严格凸函数的条件下建立了邻近梯度法的线性收敛性。

邻近梯度算法;线性收敛性;Group Lasso

0 引 言

考虑如下Group Lasso正则化问题:

(1)

其中f(x)是一个光滑的凸函数，J是{1,2,…,n}的一个划分。形如式(1)的凸优化问题有广泛应用，如在信号和图像去噪(参见文献[1])以及数据挖掘和分类(参见文献[2], 文献[3])等方面，主要考虑如下Lasso问题：

(2)

问题(2)是问题(1)的特殊形式，其中J={{1},{2},…,{n}}。

下面的Group Lasso问题(参见文献[4])作为Lasso问题的一个推广也是问题(1)的特殊形式：

Hale等在文献[5]中考虑如下带l1正则化的极小化问题:

min{μf(x)+‖x‖1},

(3)

在仅要求f(x)是凸函数的条件下，证明了邻近梯度算法(PGM)求解问题(3)时具有Q线性收敛速率。

Zhang等在文献[6]针对如下问题分析了PGM的线性收敛性:

其中,h:Rm→R是一个连续可微强凸函数，A∈Rm×Rn是一个给定的矩阵，BJ是一个与xJ相容的非奇异矩阵。李英毅等[7]提出一类修正邻近梯度法并分析了算法的收敛性。裴慧敏[8]研究了交替邻近梯度法的收敛性分析。

受上述工作的启发，本文考虑利用PGM求解问题(1)的线性收敛性。

1 邻近梯度方法

为了介绍PGM，首先给出Moreu-Yoshida邻近算子的定义(参见文献[9])。函数φ(x)的Moreu-Yoshida邻近算子proxφ:Rn→Rn定义如下:

问题(1)的最优解等价于如下不动点方程的解:

x=proxμφ(x)(x-μf(x)),

xk+1=proxμkφ(x)(xk-μkf(xk))，

其中，步长μk>0。上式等价于:

(4)

对于μ>0，令:

则:

⟺0J∈∀J∈J

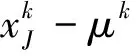
因此，对于J∈J，有:

(5)

设X*是问题(1)的解集，则：

由此可得:

(6)

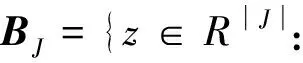
证明 证明分成四种情形。

c2=a2+b2-2abcosA。

由式(5)，可得:

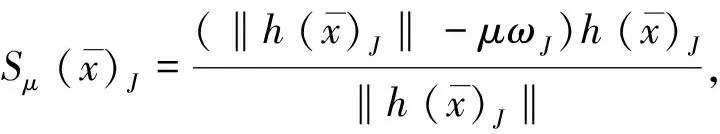
c′2= (a-t)2+(b-t)2-2(a-t)(b-t)cosA=

a2-2at+t2+b2-2bt+t2-2(ab-(a+b)t+t2)cosA=

(a2+b2-2abcosA)-2at-2bt+2t2-2(-(a+b)t+t2)cosA=

c2+2t(t-a-b)-2t(t-a-b)cosA=c2+2t(t-a-b)(1-cosA)≤c2,

由于a>t,b>t，所以A=0当且仅当存在一个λ∈(0,+∞)，使得h(x)J=λh(y)J。

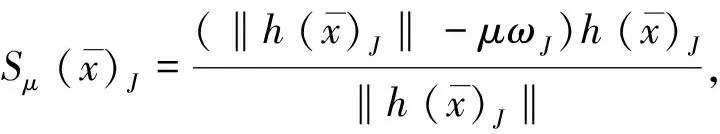
所以：

若等式成立则存在λ∈(0,+∞)使得h(x)J=λh(y)J。因此等式成立等价于：

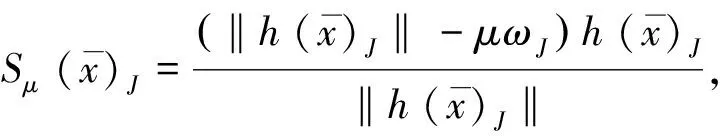
所以:

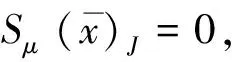
所以:

2 收敛性与收敛率分析

本文分析邻近梯度算法(4)的收敛性及收敛率。首先给出如下假设条件。

假设1 问题(1)的最优解集X*非空，且存在集合：

Ω={x:‖x-x*‖≤ρ}⊆Rn,

其中x*∈X*，ρ>0，使得f∈C2(Ω)，对任意x∈Ω有H:=2f(x)0，并且:

由中值定理可得，对于任意的x,y∈Ω，有:

‖h(x)-h(y)‖≤‖x-y‖。

推论1 假设1成立，则存在g*∈Rn，使得:

f(x*)≡g*, ∀x*∈X*∩Ω。

证明 对任意的x,y∈X*∩Ω，有:

‖xJ-yJ‖=‖S(x)J-S(y)J‖≤‖h(x)J-h(y)J‖≤‖xJ-yJ‖, ∀J∈J,

其中等式由(6)式可得，第一个不等式由引理1得到，第二个不等式由引理2得。由上式有:

‖h(x)-h(y)‖=‖x-y‖。

下面的定义在PGM算法(4)收敛性的分析中将起到关键性的作用。

定义1 设g*是推论1中定义向量，定义:

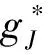
若L≠Φ，定义:

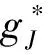
由式(6)可知，∪J∈L∪EJ={1,2,…,n}，且对任意x*∈X*有:

由上式可知，对任意x∈X*和J∈L有：

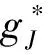
因此，对任意x*∈X*有:

η=min{μωJ-‖h(x*)J‖:J∈L}>0。

2.1 全局和有限步收敛

引理3 假设1成立，设μ>0。若x∈Ω使得:

‖Sμ(x)-Sμ(x*)‖≡‖Sμ(x)-x*‖=‖x-x*‖,

则x=Sμ(x)，进而x是问题(1)的一个解。

证明 由引理1可得:

‖Sμ(x)J-Sμ(x*)J‖≤‖h(x)J-h(x*)J‖, ∀J∈J,

(7)

因此:

‖Sμ(x)-Sμ(x*)‖≤‖h(x)-h(x*)‖。

由引理2可得:

‖h(x)-h(x*)‖≤‖x-x*‖,

所以

‖Sμ(x)-Sμ(x*)‖=‖h(x)-h(x*)‖=‖x-x*‖。

(8)

由引理1可得：

所以:

Sμ(x)J=xJ-μf(x)J+μf(x*)J, ∀J∈J,

定理1 假设1成立，如果初始点x0∈Ω，则PGM算法(4)产生的迭代序列{xk}收敛，且极限点属于X*∩Ω。

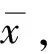
(9)

序列{‖xk-x*‖}单调不增且有界。故存在极限，结合式(9)有:

(10)

由函数S(·)的连续性可知，

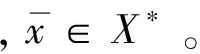
下面的定理表明PGM算法(4)对于L中指标对应的变量块具有有限步收敛性。

‖h(xk)J-(h(x*)J‖-(μωJ-‖h(x*)J‖)≤

‖h(xk)J-(h(x*)J‖-η, ∀J∈L,

其中，最后一个不等式由式(7)可得，所以:

由引理1可得:

所以:

‖xk+1-x*‖2≤‖h(xk)-h(x*)‖2-η2。

又由引理2中h(x)是非扩张映射，可得:

‖xk+1-x*2‖≤‖xk-x*‖2-η2,

2.2 线性收敛速率

本节分析PGM算法(4)的线性收敛率。在“2.1节”中，已经证明了由PGM算法(4)产生的序列{xk}收敛。本小节假设:

定理3 假设1成立，若:

证明 由定理2知对充分大的k，有:

对充分大的k，由引理1可得

3 总 结

本文针对Group Lasso正则化问题借助不动点算子分析了邻近梯度算法的全局收敛性、有限收敛性及收敛率。

[1] TROPP J A. Convex programming methods for identifying sparse signals[J]. IEEE Trans Info Theory, 2006,51:1030-1051.

[2] SARDY S，TSENG P. Automatic nonlinear fitting of additive models, robust and generalized, with wavelets[J]. J Comput Graph Statist, 2004, 13: 283-309.

[3] WANG L.Efficient Regularized solution path algorithms with applications in machine learning and data mining[D]. University of Michigan，2008.

[4] MEIER L，VAN DE GEER S，BUHLMANN P.The group Lasso for logistic regression[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology)，2008，70(1): 53-71.

[5] HALE E T, YIN W, ZHANG Y. Fixed-point continuation for 11-minimization: Methodology and convergence[J]. SIAM Journal on Optimization, 2008, 19(3):1107-1130.

[6] ZHANG H B，WEI J，LI M X，et al.On proximal gradient method for the convex problems regularized with the group reproducing kernel norm[J]. Journal of Global Optimization，2014，58(1): 169-188.

[7] 李英毅，张海斌，高欢.一类修正邻近梯度法及其收敛性[J]. 数学物理学报， 2015,35A(6):1136-1145.

[8] 裴慧敏.交替邻近梯度法的收敛性分析及其应用[D]. 北京工业大学， 2014.

[9] ROCKAFELLAR R T，WETS R J.Variational analysis.grundlehren der mathematischen wissenschaften[M]. Berlin: Springer-Verlag，1998.

(责任编辑 梁碧芬)

Linear convergence of proximal gradient method for Group Lasso regularized problems

CHAO Mian-tao, DENG Zhao, TANG Chun-ming

(College of Mathematics and Information Science, Guangxi University, Guangxi Colleges and Universities Key Laboratory of Mathematics and its Applications, Nanning 530004, China)

A class of non-smooth convex optimization problems whose objective function is a convex differentiable function regularized by the Group Lasso norm is studied. Using the theory of fixed point iteration, the global convergence and finite convergence of the proximal gradient method are analyzed.In particular,the linear convergence of the proximal gradient method is established without assuming strict convexity of the convex differentiable function.

proximal gradient method; linear convergence; Group Lasso

2016-07-08；

2016-09-21

国家自然科学基金资助项目(11301095;11601095)；广西自然科学基金资助项目(2013GXNSFAA019013;2016GXNSFBA380185);复杂系统优化与大数据处理广西高校重点实验室开放课题资助项目(2016CSOBDP0203，2016CSOBDP0204)

唐春明(1979—)，男，广西灵川人，广西大学教授，博士；E-mail: cmtang@gxu.edu.cn。

晁绵涛，邓钊，唐春明.Group Lasso正则化问题的邻近梯度算法的线性收敛性[J].广西大学学报(自然科学版)，2016，41(6)：2071-2077.

10.13624/j.cnki.issn.1001-7445.2016.2071

O221.2

A

1001-7445(2016)06-2071-07