凹版印刷机中的锥度张力控制研究

彭 燕

（渭南师范学院 物理与电气工程学院电气工程系，渭南 714000）

设计与应用

凹版印刷机中的锥度张力控制研究

彭 燕

（渭南师范学院 物理与电气工程学院电气工程系，渭南 714000）

针对凹印机中的锥度张力运行情况，详细分析张力的产生及其锥度张力原理，利用近似方法对锥度张力运行进行建模，张力控制器采用积分分离PID的办法，给出了锥度张力整个系统运行原理，采用MATLAB进行仿真，从仿真结果可以看出锥度张力能满足凹印机生产要求，凹印机正常运行且不会出现褶皱等问题。

锥度张力；积分分离PID；MATLAB仿真；凹版印刷机

0 引言

随着计算机技术和光纤传感器等技术的发展，提高印刷机速度和精度，优化印刷效果，使凹印机智能化、自动化，成为印刷工业发展的必然过程。在凹刷机上，张力控制的好坏直接影响印刷产品质量，是整机的核心。而目前凹印机张力控制系统的配置有三种：二段闭环式张力控制系统、三段闭环式张力控制系统和四段式闭环式张力控制系统[1]。四段闭环式张力控制被我国高档凹印机广泛使用，收放卷段（即收料牵引到收料单元，放料牵引到放料单元）由于卷径的变化，使张力成为一种无规律的变化模式，因此研究收放卷段的非线性、速度和张力强耦合的复杂控制系统就成为研究的重要课题。凹印机中张力控制大多采用恒张力控制，这样容易使卷绕在轴上的材料内松外紧以至于出现褶皱。

为了克服这一现象，本文在研究四段闭式凹印机中收卷段张力控制模型的基础上，采用积分分离PID控制方式，实现收卷段锥度张力（即系统卷绕张力随半径的增大而减小）控制。并利用凹印机生产过程说明锥度张力的优越性。

1 收卷段的锥度张力控制

1.1 张力的产生

图1是两卷辊之间的卷材受力示意图，其中，V1， V2分别是辊1和辊2的线速度，L表示两个卷辊轴心之间的距离。根据胡克定律F=kx得：

图1 卷材受力示意图

ε表示卷材的弹性模量，σ表示卷材的横截面积，t为机器反应时间。V2-V1决定了张力的变化快慢，对张力的控制可以通过控制相邻两卷辊的速度差来实现。可见，收卷段收卷牵引和收料辊之间的线速度差是张力的形成原因，卷绕张力F的计算公式为式(1)。

1.2 锥度张力控制

锥度张力指卷绕过程中，系统卷绕张力随半径的增大而减小。其线性锥度张力模型如图2所示。

F0表示张力初始值，F1表示张力结束值，卷轴的直径为Dmin，进行锥度张力控制的初始卷径为D0，张力控制结束时的卷径为D1，如式(2)所示。

图2 线性锥度张力模型

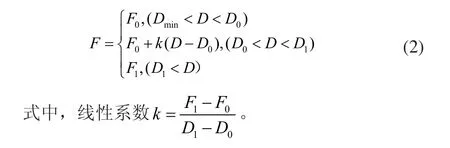
由于凹印机的卷材厚度很小，所以收卷卷径在一定时间段内的值可以看做是恒定的。因此，张力模型可以修正为图3。在实际卷绕过程中，可以将收卷过程分为几个时间段，在一个时间段内张力是恒定的，便得工程上的F/t锥度张力模型。

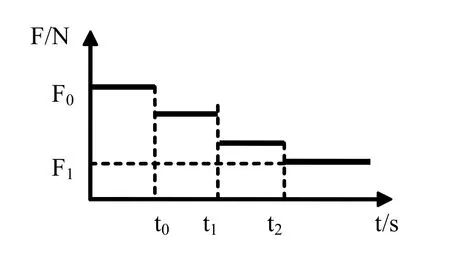
图3 F-t的锥度张力模型

在四段式闭环式张力控制系统[2]中，牵引和收卷部分均由电机控制，需采用一定的方法同时控制电机速度，图4是以收卷单元为主要被控对象的电机控制锥度张力系统。

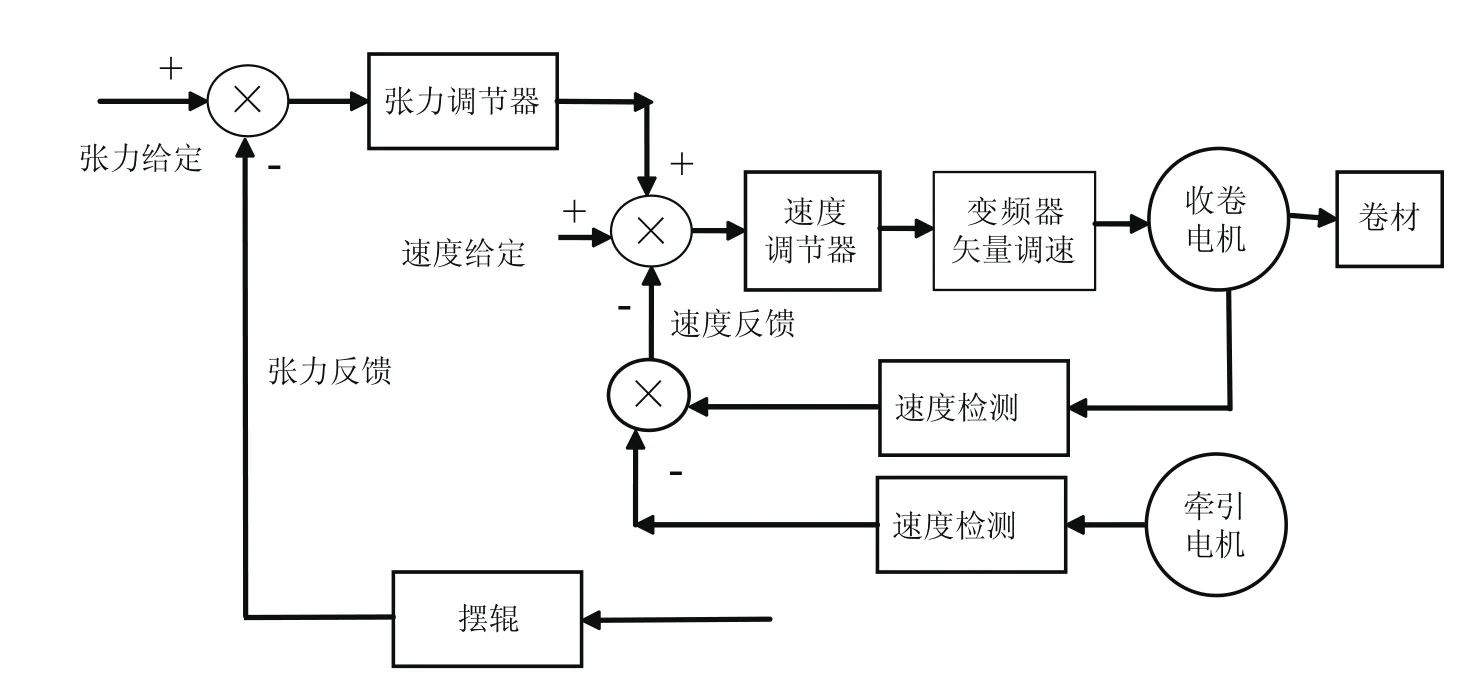
图4 收卷单元电机锥度张力控制模型

1.3 锥度张力控制器

常用的电机张力控制系统是锥度张力控制系统[3]，如图4所示。控制器常采用的算法有PID控制、模糊控制等。系统硬件组成有PLC、变频器、摆辊和编码器等。系统以收卷单元电机为主且轴上安装编码器，能实时测量精确的速度值；将计算出的实际收卷线速度反馈到PLC中，再经过PID调节控制收卷电机转速形成速度闭环控制。张力闭环是速度环的串级环，张力由摆辊测量变送回PLC中，再与设定的锥度分段张力比较由PID调节器调整收卷电机转速形成。

考虑要防止非线性系统的强耦合、实时性和非线性，锥度张力控制器采用积分分离的PID控制算法，算法如式(3)所示。当被控制量与设定值的误差较大时，取消积分作用，可抑制超调量，提高系统稳定性；当被控制量接近设定值时，积分环节可消除静差，提高张力控制精度。

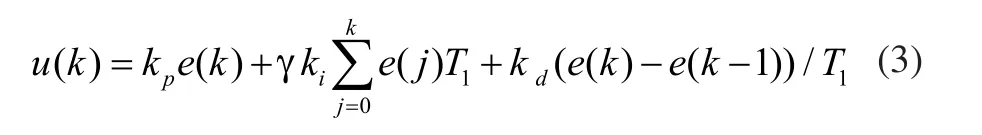
式中e(k)是k时刻输入输出的差值，T1是采样周期，kp、ki和kd分别为比例、积分、微分系数，γ是积分项的开关系数，ε为实际系统设定的阈值。

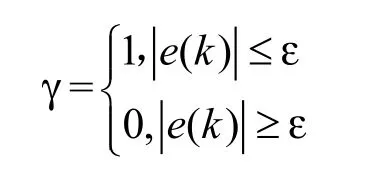
2 锥度张力控制系统模型

2.1 收卷段张力模型

根据静态力矩平衡关系，在收卷过程中有：

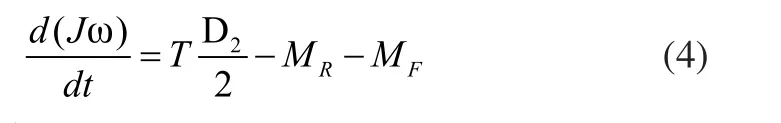
其中，MR是收卷辊的制动力矩，ω为收卷卷辊的角速度，T是总张力，单位kN，MF=Bfω是阻尼力矩，Bf为阻尼系数，J是转动惯量。卷绕过程中，收卷辊的直径越来越大，所以卷辊的转动惯量也越来越大，很明显这是个非线性的时变系统。J由两部分组成，一部分是卷材的转动惯量，一部分是卷芯的转动惯量。收卷段张力T主要受速度和卷辊半径变化的影响，设制动力矩和摩擦力矩为恒定值，当卷径不变时，收卷辊张力T与速度的传递函数可以简化为：

2.2 摆辊模型

摆辊的两端安装了电位计，摆辊摆动带动电位计运动，不同的摆幅反映了不同的张力变化，具体摆辊的位置反映为不同的电位值。因此，摆辊的摆角θ直接反映了卷材张力的波动∆T。

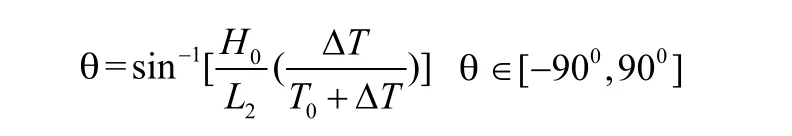
实际上θ被限制得很小，通常限制在θ∈[−180,180]之间。由摆辊摆角θ可得电位计摆角θs，可以得到一个电位计检测电压u，

2.3 直流电机

交流异步电机通过电机动力学方程，可以将交流电机的三维静止交流坐标转换到二维旋转直流坐标系，然后得到转矩与电流公式[2]，交流电机类似于直流电机的模型，根据传递函数建立数学模型如图5所示。

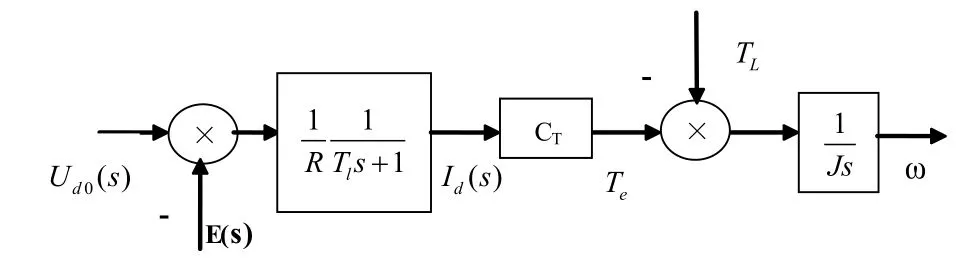
图5 直流电机动态结构框图

2.4 收卷单元张力控制系统

收卷单元张力控制系统如图6所示，是一个串级控制系统。系统包含内环（速度环）和外环（位置环），根据外环张力的变化，调节内部电机转速，进而实现张力调节。本系统中速度环采用常规PID调节，外环使用积分分离PID。

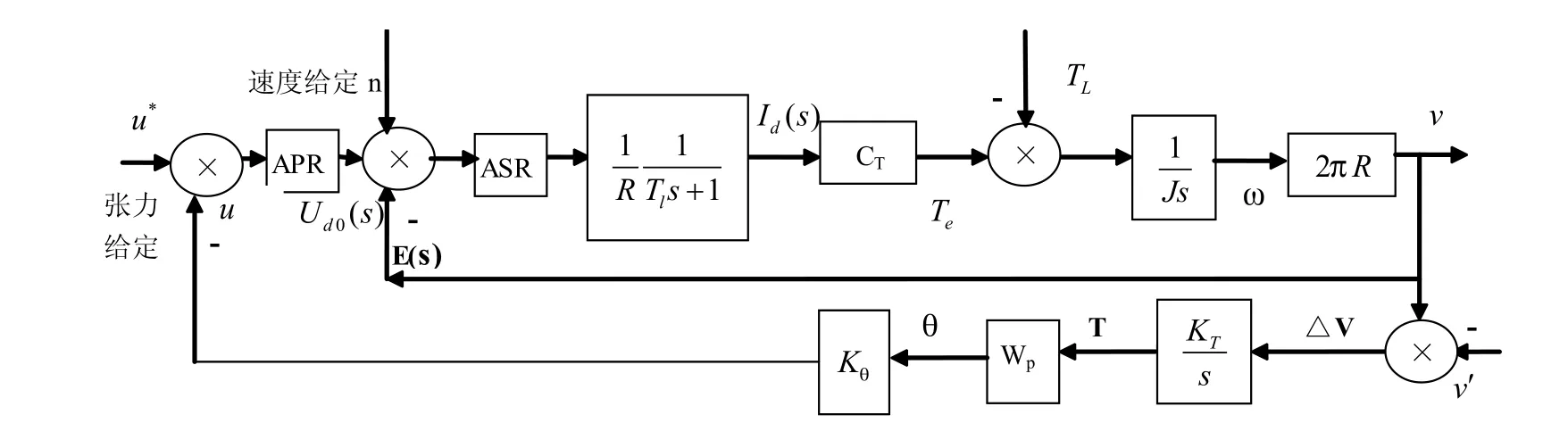
图6 收卷单元张力数学模型

3 锥度张力控制系统仿真

仿真模型[4,5]如图8所示，可以认为内环（速度环）是一个惯性环节，速度环外部的张力环也被建模为一个惯性环节，内环采用比例控制，外环采用积分分离PID控制，采用选择开关实现积分分离。每隔一定时间改变step信号实现锥度张力控制。

仿真结果如图7所示。

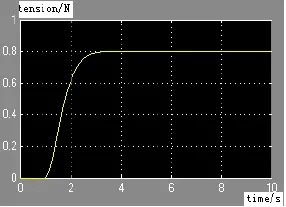
图7 锥度张力仿真结果

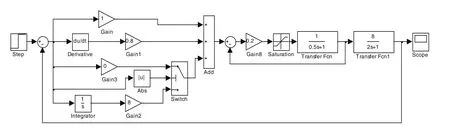
图8 锥度张力控制仿真模型

4 结束语

对速度环实验500r/min的情况下，电机速度很快达到设定值。张力环实验卷径在92mm～800mm范围时，所整定的PID参数满足四个阶段收卷段的不同任务要求，正常运行时系统能够运行在100m/min～200m/min的速度范围内，且系统出现外部干扰时能够很快调节摆辊位置，使其恢复到垂直位置。

从仿真结果看，该锥度张力控制模型适应于凹版印刷机需要，比传统恒值控制方式[6,7]要优越许多，但是这种控制方法仍然有缺陷，在锥度突变位置，机器仍然会出现或多或少的振荡，因此这种方式仍然需要改进。

[1] 陈满儒,惠晓妮.矢量变频器在凹版印刷机上的张力控制[J].包装工程,2007,28(11):89-91.

[2] 史廷永.基于H鲁棒控制的凹印机张力控制系统研究[D].中南大学,2009.

[3] Man Gyun Na and Jae Hyung Lim. A Fuzzy Controller Based on Self-tunning Rules for the Nuclear Steam Generator Water Level [J]. KAME International Journal,1977,11(5):485-493.

[4] SONG S H, SUL S K. Design and control of multi-span tension simulator[J].IEEE Ind Appl,2000,36(2):640-648.

[5] Hyunkyoo Kang, Reinhard R. Baumann. Mathematical modeling and simulations for machine directional register in hybrid rollto-roll printing systems[J].International Journal of Precision Engineering and Manufacturing,2014, 15(10):2109-2116.

[6] Ganeshthangaraj Ponniah,Muhammad Zubair, et al. Fuzzy decoupling to reduce propagation of tension disturbances in rollto-roll system[J].The International of Advanced Manufacturing Technology,2014,71:153-163.

[7] TRAN T T,CHOI K H, et al. Web tension and velocity control of two-span roll-to-roll system for printed electronics[J].J Adv Mech Des Syst,2011,5(4):329-346.

图6 理想偏角与实际偏角比较

图中，未使用转向梯形的α−β曲线由连续曲线表示，使用转向梯形后的α−β曲线由离散的圆圈表示，二者在内侧轮转角为0～0.4rad时基本吻合，满足设计要求。

4 结论

文章首先对智能轮椅进行运动学分析，分别得到了轮椅两前轮在轮椅转弯过程中偏角之间的关系，并根据阿克曼原理得到了四个车轮在局部参考系和整体参考系中的位姿；最后依据智能轮椅在转弯过程中两前轮的偏角函数关系设计了转向梯形，以此减小前轮与地面之间水平滑动，提高了轮椅的灵活性和操控性。

参考文献：

[1] 任孝平,蔡自兴.基于阿克曼原理的车式移动机器人运动学建模[J].智能系统学报,2009,4(6).

[2] 常勇,马书根,王洪光,谈大龙,宋小康.轮式移动机器人运动学建模方法[J].机械工程学报,2010,46(5).

[3] 肖启瑞.车辆工程仿真与分析:基于MATLAB的实现[M].北京:机械工业出版社,2012.

Taper tension in gravure printing machine

PENG Yan

TS803.6

A

1009-0134(2016)12-0081-04

2016-02-28

彭燕（1984 -），女，陕西人，讲师，硕士，主要从事电气工程、自动控制领域的教学和研究工作。