不同加载速率下混凝土损伤阶段的划分

马小亮，彭 刚，肖 杰，胡伟华,2

(1.三峡大学土木与建筑学院，湖北宜昌 443002; 2.十堰市建筑设计研究院，湖北十堰 443000)



不同加载速率下混凝土损伤阶段的划分

马小亮1，彭 刚1，肖 杰1，胡伟华1,2

(1.三峡大学土木与建筑学院，湖北宜昌 443002; 2.十堰市建筑设计研究院，湖北十堰 443000)

在不同加载速率(10-5/s，10-4/s，10-3/s，10-2/s)下进行混凝土试块单轴受压试验，基于改进后的Weibull模型构建了损伤变量，并在应变空间下对损伤曲线做了进一步的细化研究。首先根据损伤曲线的特点，提出了合理方法来确定损伤界点在曲线上的位置，两个界点将损伤曲线划分为3个损伤阶段。在此基础上，探讨了加载速率对损伤界点、损伤阶段长度的影响规律。研究结果表明：①第一损伤界点对加载速率的提高较为敏感，并随加载速率的增大几乎呈线性发展，第二损伤界点对加载速率的提高不敏感；②加载速率的提高使3个损伤阶段的区间长度重新分配，对前两个损伤阶段影响较大，对第3个损伤阶段区间长度的影响较小；③两损伤界点位置基本对称分布于峰值应变两侧，大部分损伤集中在峰值应力1倍的峰值应变范围内，且两损伤界点对应的应变水平比值约为3.5，并随加载速率的提高而减小。

混凝土； 加载速率； 阶段划分； 损伤界点； 损伤阶段

混凝土在工作过程中，会受到各种作用而产生损伤。损伤的发展变化规律非常复杂，因为受力情况、加载速率、荷载历时和围压大小等都会对其造成影响。在Dougill将损伤理论引入混凝土的研究后，关于混凝土损伤机理的研究进展迅猛，提出了许多损伤本构模型。关于混凝土损伤方面的研究已经有很多，并取得了很好的进展。1986年,J.Mazars[1]引入弹性损伤能释放率建立损伤准则,并基于应力张量分解而建立了D.Mazars模型。李杰等[2-5]基于损伤能释放 ,考虑损伤和塑性的耦合效应,建立了以热力学为基础的双标量弹塑性损伤模型。D.Breysse[6]从宏观和微观两层次同时出发，并结合连续介质损伤力学模型建立了混凝土的本构关系。李庆斌等[7]从混凝土动力和静力损伤之间的关系入手,分析了动力与静力损伤之间初始弹性模量的差别,以静力损伤本构理论为基础，构建了混凝土动力损伤的本构方程。宋玉普等[8]考虑尺寸效应与骨料湿筛效应对损伤发展的影响,并结合内时理论和损伤力学理论,构建了与骨料级配相关的内时损伤本构模型。肖诗云等[9]基于试验分析了混凝土的动态特性,基于切线模量的退化考察了损伤的发展规律,分别在应力空间和应变空间下分析了混凝土损伤变化，并考察了随加载速率的增大其损伤槛值的推移规律。李杰等[10]考虑混凝土的随机性，引入包含黏性元件和弹性元件的细观模型，推导建立了混凝土动力损伤模型，并通过算例进行了验证。彭刚等[11-12]通过试验对有压孔隙水环境中的混凝土动态抗压性能进行研究，探究了有压孔隙水的存在对混凝土损伤特性的影响。

然而现有的研究多集中在损伤本构模型的构建和损伤机理的理论分析方面，对混凝土损伤过程中的一些具体特点，比如损伤界点和损伤阶段的研究比较少见。若能通过大量试验分析，将混凝土损伤过程合理划分为若干阶段，并对每一阶段的损伤规律进行归纳总结，有助于加深对混凝土损伤规律的认识。所以对混凝土损伤发展曲线进一步的细化分析，具有较高的理论和实践意义。但要进行损伤曲线的阶段划分，先要建立合理的划分标准。本文从试验数据出发，分析混凝土的损伤全曲线特点，分析了单轴受压情况下不同加载速率时混凝土损伤阶段的变化规律，探讨了在单轴受压混凝土损伤曲线阶段划分的方法。

1 试验过程

1.1 试件制备及养护

试验采用尺寸为150 mm×150 mm×150 mm的立方体试件，混凝土强度等级为C30，水泥为42.5的普通硅酸盐水泥，由宜昌市三峡水泥有限公司生产。粗骨料为连续级配的碎石，直径10～20 mm，细骨料为宜昌地区连续级配河砂。采用普通自来水进行搅拌。配合比根据《普通混凝土配合比设计规程》(JGJ 55—2011)进行理论计算与试配，最后采用配合比为10.56∶2.55∶3.83(水泥∶水∶粗骨料∶细骨料)。为使混合搅拌较为均匀，采用先机械干拌后加水湿拌的机械搅拌方式，即：先将称量好的粗骨料、细骨料和水泥倒在搅拌机内，搅拌均匀，然后加入称量好的水进行搅拌。搅拌完成后，将混凝土倒入安装好的钢模中，先进行人工振捣，再放在振动台振捣至密实，待混合料高出钢模口平面1 cm左右时刮出多余混合料并抹平表面。试件浇筑完成2 d后，进行脱模编号并将其移至养护室。标准条件下养护270 d后方可进行试验。

1.2 试验设备及加载方案

图1 力学试验设备Fig.1 Mechanical test equipment

试验采用的大型多功能动静力三轴仪，由三峡大学与长春市朝阳试验仪器有限公司联合研制。整个试验系统由加载框架、数据采集系统和EDC控制器3部分组成，见图1。仪器系统由微机控制电液伺服，3个独立油缸来施加荷载，竖向最大出力10 000 kN，双向水平最大出力5 000 kN；竖向行程400 mm，水平行程200 mm。系统可实时测量各个方向的位移，精度可达10-3mm。EDC控制和数据采集系统最大可存储30万组数据样本，最大采样频率0.002 s，可采用负荷、变形、位移等多种方式对3个方向的加载速度进行调控，可实现矩形波、三角形波、正弦波、随机波等多种波形的加载方式，能实时自动采集数据并反馈相关信息，实现存储、处理试验数据的同步进行。

研究地震荷载作用时混凝土动态特性，加载速率为10-4/s ～10-2/s，设10-5/s为准静态应变率，所以共取4种加载速率(10-5/s，10-4/s，10-3/s，10-2/s)。加载方式为：在4种不同加载速率下，分别对养护好的试块在多功能三轴仪上单轴竖向等应变加压至破坏，为保证数据可靠，当试件加载数据离散性较大时,启用备用试件重新进行加载试验。

2 试验结果分析

2.1 Weibull-Lognormal本构模型

王春来等[13]认为混凝土材料单轴压缩时的本构关系服从Weibull统计分布特点，并结合应变等效原理建立了混凝土本构模型：

(1)

式中：E为弹性模量；m为曲线形状控制参数。初始弹模、峰荷应变值和m值可由试验确定。

文献[14]却指出，当混凝土强度超过一定值后，混凝土峰值后应力与应变的关系偏离Weibull统计分布的特点，并对其进行了修改。对峰值后建立的应力-应变关系为：

(2)

其几何边界条件由ε=εpk,dσ/dε=0，ε=εpk,σ=σpk决定，对式(2)求导可得

a=σpk

(3)

表1 模型拟合参数

Tab.1 Fitting parameters of the model

加载速率/s-1mtR210-51.32300.67680.983410-41.33340.54780.955510-31.35480.76370.988410-21.38550.65610.9862

则峰值后的应力-应变关系为

(4)

式中：εpk和σpk为峰值应变和峰值应力；m和t分别为上升段和下降段的形状控制参数，可使用MATLAB对试验数据进行拟合，通过迭代计算确定。具体拟合参数如表1所示，将试验所得数据按上面改进后的模型拟合可得图2的对比曲线。从拟合度及拟合图像来看，改进后的Weibull模型能够较好拟合单轴受压时的应力应变曲线。

图2 不同加载速率时应力应变拟合曲线Fig.2 Fitting curves of stress and strain under different loading rates

2.2 损伤变量方程的构建

根据Lemaitre[15]的应变等价原理有

σ=E(1-D)ε

(5)

将式(1)和(4)分别代入式(5)得到Weibull分段损伤模型为

(6)

根据该模型，将所得数据带入可得混凝土单轴损伤演化与应力应变的关系。

2.3 损伤界点的确定

分析图3中损伤过程可知，4种不同应变下的损伤曲线形状相似，随着加载率的变化，损伤3阶段起点对应的应变水平也在不断变化。损伤演化过程有2个明显变化的界点，将曲线分为3个阶段。根据损伤随应变水平的变化，对损伤曲线求导，根据所求导数值，即曲线斜率的突变来确定界点的具体位置。根据损伤曲线的特点，3个阶段分别是：第1阶段，损伤初始发展阶段，该阶段损伤值基本在零附近波动，可认为没有损伤产生；第2阶段，损伤萌发及稳定发展阶段，此阶段混凝土损伤值增长迅速，增加幅度大；第3阶段，损伤不稳定阶段，此阶段处于较高应力水平下，损伤发展较快，直至试件破坏。其中损伤第1阶段的终点或者第2阶段的起点为损伤第一界点，损伤第2阶段的终点或者第3阶段的起点为损伤第二界点。应力水平区间长度为相应界点的对应应力水平的差值。对于损伤曲线上损伤界点的选取，目前多通过曲线的形状来直接指定，然而这种直接指定的方法显得不够精细。下面具体介绍确定损伤界点的方法。

图3 不同加载速率时损伤随应变水平的变化Fig.3 Changes of concrete damage with strain levels under different loading rates

2.3.1 损伤第一界点的确定 根据图3可见，在应变空间下，损伤曲线由初始阶段的凹曲线逐渐转变为损伤快速发展阶段及损伤稳定发展阶段的凸曲线。在此，将该凹凸分界点取为第一界点。从其数学意义来看，它表征了曲线增长趋势的转折，同时从损伤曲线可以看到该点之前损伤比较小，这也符合对损伤第一阶段的定义，所以将其选为损伤第一界点比较合理。从图上可见该点位于峰值应变之前，根据所选取的Weibull-Lognormal本构模型，该段的曲线方程为：

(7)

取ε/εpk=x，对上升段(0≤ε≤εpk)损伤曲线方程求导可得：

(8)

表2 模型拟合参数及第一界点对应应变水平

Tab.2 Fitting parameters of model and first damage point corresponding to strain levels

加载速率/(s-1)拟合参数m应变水平x110-51.32300.425610-41.36380.438810-31.35480.465410-21.57050.5026

对上式再进行求导，可得到其二阶导函数如下：

(9)

令D″=0，可求得

(10)

将表1中的拟合参数值带入上式可得到不同加载速率时的x1的值，详见表2。

2.3.2 第二界点的确定 在医学上常通过ROC曲线中特异性和灵敏度两个指标来确定药物性状阀值[16]。在此，借鉴该方法，以横坐标应变为灵敏度，纵坐标损伤值为特异性确定损伤曲线上的第二损伤界点。如图4所示，N点为借鉴ROC曲线确定临界点方法得到的临界点，M点为损伤曲线与应力应变曲线的交点。根据计算发现M点与N点在曲线上相距很近，故用M点代替N点作为第二损伤界点。

在图3中，将应力应变全曲线与损伤曲线归一后放在同一图表中。根据以上分析，求第二损伤界点的问题转化为求损伤曲线与应力应变曲线交点的问题。将两应力应变曲线的方程与损伤曲线第2部分的方程联立，即可求得交点的值。过程如下：

图4 第二损伤界点位置Fig.4 Second damage point position

(11)

将上式化简可得：

(12)

表3 模型拟合参数及第二界点对应应变水平

用Matlab对该方程进行求解可得。式(2)中，x可以用参数t来表示，将试验得到的参数t带入式(12)即可求得x2的值。不同加载速率时的x2值见表3。

2.4 损伤界点、损伤阶段随加载速率的变化关系

根据表2、表3求出应变空间下损伤界点的值，绘制损伤界点随加载速率的变化曲线，如图5和6所示，可以看出加载速率的提高使得第一损伤界点向应变水平较高的方向迁移，而第二损伤界点对加载速率的变化不敏感；4种速率下，第一损伤界点约值在0.46，即说明第一损伤界点在应变空间下一般出现在峰值应变40%处。4种速率下，第二界点均值约为1.6，说明第二损伤界点在应变空间下一般出现在1.6倍的峰值应变处。因为第一损伤界点在加载速率提高时其对应的应变水平也对应增长，所以此处对其进行线性拟合，拟合曲线的方程为y=0.025 8x+0.548 3,拟合精度为0.979。对比数据可知，第二损伤界点与第一损伤界点对应的应变水平之比随加载速率的提高而降低，但浮动范围为3.2～3.8，可取其平均值3.5。同时可以发现，在峰值应力附近损伤发展最快，大部分损伤集中在峰值应力左右一定的范围内，两损伤界点基本在峰值应力两侧对称分布。这主要是由于在峰值应力附近时混凝土内部承受较高压力，内部存在缺陷的地方大量产生裂缝，原有比较细小的裂缝迅速扩展，导致损伤的大量产生。加载速率越快，内部损伤产生越剧烈，损伤越向峰值应力附近集中。

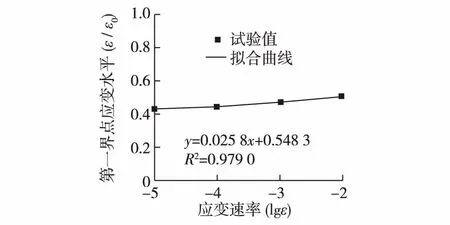
图5 不同加载速率下第一损伤界点及其拟合曲线Fig.5 First damage boundary point under different loading rates and fitting curve

图6 第二损伤界点随加载速率的变化Fig.6 Second damage point variation with changes in loading rates

损伤界点的变化必然会引起损伤三阶段应变水平区间的变化，加载速率为10-5/s时损伤3个阶段过程分配比例分别为10.64%，29.88%，59.48%；加载速率为10-4/s时分别为10.97%，29.41%，59.62%；加载速率为10-3/s时分别为11.64%，28.51%，59.85%；加载速率为10-2/s时分别为12.56%，27.70%，59.74%。数据说明加载速率改变了损伤3个阶段的分配比例，损伤初始发展阶段与损伤稳定发展阶段对加载速率的变化敏感，损伤不稳定阶段对加载速率的变化不敏感。从数据可见，应力峰值总是包含在损伤稳定发展阶段内，随加载速率的提高，第1损伤阶段区间长度在减小，第2损伤区间长度增大，第3损伤区间长度变化不大，也就是说加载速率的变化主要体现在对前两个损伤阶段的影响。

3 结 语

进行了不同加载速率下的单轴受压试验，基于Weibull-Lognormal本构模型建立损伤曲线的表达式，在此基础上在应变空间下进一步探究了损伤界点、损伤阶段随加载速率的变化规律，由此得出如下结论：

(1)混凝土单轴受压时两个损伤界点将损伤曲线分为3个阶段，第一个界点取为应变空间下损伤曲线凹凸变化分界点，第二损伤界点取为损伤曲线与应力应变全曲线的交点，两界点大致对称分列于峰值应变两侧。

(2)加载速率的提高使得损伤第一界点向应变水平较高的方向推移，界点的推移引起了损伤三阶段应变水平区间长度的变化。虽然加载速率对损伤界点位置有影响，但大致位置基本确定，损伤初始发展阶段最大应变在峰值应变40%附近，损伤稳定发展阶段最大应变在1.6倍峰值应变附近。

(3)加载速率的提高改变了损伤三阶段的分配比例，损伤初始发展阶段随着加载速率的提高其应变水平区间长度呈增加趋势，损伤稳定发展阶段应变水平区间长度呈减小趋势，损伤不稳定发展阶段的应变水平区间长度变化不明显。也就是说，加载速率的提高主要改变了前两个损伤阶段的分配，对第3个损伤阶段区间长度的影响较小。

[1]MAZARS J.A description of micro- and macro-scale damage of concrete structures[J].Engineering Facture Mechanics,1986,25：729- 737.

[2]李杰,吴建营.混凝土弹塑性损伤本构模型研究Ⅰ：基本公式[J].土木工程学报,2005,38(9)：14- 20.(LI Jie,WU Jian-ying.Elastoplastic damage constitutive model for concrete based on damage energy release rates,part1：Basic formulations[J].China Civil Engineering Journal,2005,38(9)：14- 20.(in Chinese))

[3]LI Jie,WU Jian-ying.Energy-based CDM model for nonlinear analysis of confined concrete structures[R].American Concrete Institute,2006,SP-238：209- 221.

[4]WU Jian-ying,LI Jie,FARIA R.An energy release rate-based plastic-damage model for concrete[J].International Journal of Solids and Structures,2006,46(3/4)：583- 612.

[5]WU Jian-ying,LI Jie.Unified plastic-damage model for concrete and its applications to dynamic nonlinear analysis of structures[J].Structural Engineering and Mechanics,2007,23(5)：519- 540.

[6]BREYSSE D.Probabilistic formulation of damage evolution law of cementitious composites[J].J Engre Mech，1990,116(7)：1489- 1510.

[7]李庆斌,邓宗才,张立翔.考虑初始弹模变化的混凝土动力损伤本构模型[J].清华大学学报(自然科学版),2003,43(8)：1088- 1091.(LI Qing-bin,DENG Zong-cai,ZHANG Li-xiang.Dynamic damage constitutive model for concrete accounting for the difference of the initial elastic modulus[J].Journal of Tsinghua University(Science and Technology),2003,43(8)：1088- 1091.(in Chinese))

[8]宋玉普,王怀亮.全级配大体积混凝土的内时损伤本构模型[J].水利学报,2006,37(7)：769- 777.(SONG Yu-pu，WANG Huai-liang.The endochronic damage constitutive model of fully-graded mass concrete[J].Journal of Hydraulic Engineering,2006,37(7)：769- 777.(in Chinese))

[9]肖诗云,张剑.不同应变率下混凝土受压损伤试验研究[J].土木工程学报,2010,43(3)：40- 45.(XIAO Shi-yun,ZHANG Jian.Compressive damage experiment of concrete at different strain rates[J].China Civil Engineering Journal,2010,43(3)：40- 45.(in Chinese))

[10]李杰,曾莎洁,任晓丹.混凝土动力随机损伤本构关系[J].同济大学学报(自然科学版),2014,42(12)：1783- 1789.(LI Jie,ZENG Sha-jie,REN Xiao-dan.A stochastic rate-dependent damage model for concrete[J].Journal of Tongji University(Natural Science),2014,42(12)：1783- 1789.(in Chinese))

[11]彭刚,王乾峰,梁春华.有压孔隙水环境中的混凝土动态抗压性能研究[J].土木工程学报,2015,48(1)：11- 18.(PENG Gang,WANG Qian-feng,LIANG Chun-hua.Study on dynamic compressive properties of concrete under pore water pressure environment[J].China Civil Engineering Journal,2015,48(1)：11- 18.(in Chinese))

[12]刘博文,彭刚,邹三兵,等.循环孔隙水作用下混凝土动态特性试验研究[J].土木建筑与环境工程,2015,37(5)：88- 94.(LIU Bo-wen,PENG Gang,ZOU San-bing,et al.Experimental analysis of dynamic properties of concrete under cyclic pore water effects[J].Journal of Civil,Arehitectural & Environmental Engineering,2015,37(5)：88- 94.(in Chinese))

[13]王春来,徐必根,李庶林,等.单轴受压状态下钢纤维混凝土损伤本构模型研究[J].岩土力学,2006,27(1)：151- 154.(WANG Chun-lai,XU Bi-gen,LI Shu-lin,et al.Study on a constitutive model of damage of SFRC under uniaxial compression[J].Rock and Soil Mechanics,2006,27(1)：151- 154.(in Chinese))

[14]陈健云,白卫峰.考虑动态应变率效应的混凝土单轴拉伸统计损伤模型[J].岩石力学与工程学报,2007,26(8)：1603- 1611.(CHEN Jian-yun,BAI Wei-feng.Statcalisti damage model of concrete under uniaxial tension considering dynamic strain-rate effect[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(8)：1603- 1611.(in Chinese))

[15]LEMAITRE J.Local approach of fracture[J].Engineering Fracture Mechanics,1986,25(5/6)：523- 537.

[16]习浩,刘荣静.利用ROC曲线更好地选择血清CA15-3对乳腺癌的最佳诊断界点[J].实用医学杂志,2013,29(3)：420- 422.(XI Hao,LIU Rong-jing.Using ROC curve to better select the best point to diagnosis of serum CA15-3 for breast cancer[J].The Journal of Practical Medicine,2013,29(3)：420- 422.(in Chinese))

Damage stage division of concrete under different loading rates

MA Xiao-liang1，PENG Gang1，XIAO Jie1，HU Wei-hua1,2

(1.CollegeofCivilEngineering&Architecture,ChinaThreeGorgesUniversity,Yichang443002,China; 2.ShiyanArchitecturalDesignInstitute,Shiyan443000 ,China)

The tests on the uniaxial compression of concrete specmens have been done under the conditions of different loading rates (10-5/s,10-4/s,10-3/s,10-2/s) in this study.Based on the improved Weibull model an expression for the damage variables was set up,and the further detailed researches on the damage curves under the strain space were carried out yet.According to the characteristics of the damage curves,the establishment of a reasonable method to determine the positions of the damage critical points on the curves,and then through two damage critical points the curves are divided into three stages.On this basis,the influences of the damage critical points and the length of the stages under the different loading rates were analysed.The test analysis results show that:(1) the first damage critical point is more sensitive to the increase of the loading rates and is almost linear development process with the increase of the loading rates,the second damage critical point is not sensitive to the increase of the loading rates.(2) the increase in the loading rates made the redistribution of the interval length of the three damage stages,which has the greater influences on the first two stages and no influences on the interval length of the third stage.(3) the positions of two damage critical points are symmetrically distributed on the both sides of the peak strain,and the most of the damage is focused within the peak strain about twice as large as the peak stress,and the ratio of the stress level corresponding to two damage critical points is about 3.5 and it decreases with the increase of the loading rates.

concrete; loading rates; stage division; damage critical points; damage stages

10.16198/j.cnki.1009-640X.2016.06.013

马小亮，彭刚，肖杰，等.不同加载速率下混凝土损伤阶段的划分[J].水利水运工程学报,2016(6):90-96.(MA Xiao-liang,PENG Gang,XIAO jie,et al.Damage stage division of concrete under different loading rates[J].Hydro-Science and Engineering,2016(6):90-96.)

2015-11-13

国家自然科学基金资助项目(51279092)

马小亮(1990—)，男，甘肃陇南人，硕士研究生，主要从事混凝土材料动力特性及结构抗震研究。 E-mail：576294134@qq.com 通信作者：彭 刚(E-mail：gpeng158@126.com)

TU502+.6

A

1009-640X(2016)06-0090-07