永磁同步电机相电流测量误差分析与补偿

蔡志端 王培良 荀 倩 姜媛媛 荀博洋

(1.湖州师范学院工学院 湖州 313000 2.南京航空航天大学自动化学院 南京 211106 3.内蒙古农业大学机电工程学院 呼和浩特 010018)

永磁同步电机相电流测量误差分析与补偿

蔡志端1王培良1荀 倩1姜媛媛2荀博洋3

(1.湖州师范学院工学院 湖州 313000 2.南京航空航天大学自动化学院 南京 211106 3.内蒙古农业大学机电工程学院 呼和浩特 010018)

为减小电流测量误差，满足永磁同步电机高性能调速要求，对相电流测量误差进行了分析与补偿。首先，介绍了电流测量误差产生原理，分析了测量误差对闭环调速系统性能的影响。然后，提出了一种对d轴电流进行分段积分的补偿策略，通过对d轴电流积分得到误差项，将其补偿到测量电流中。仿真和实验结果表明偏移误差和增益误差分别会引起转矩、转速在1倍角频率和2倍角频率处振荡，补偿策略可以很好地减小测量误差，从而减小转矩和转速周期性振荡。

测量误差 偏移误差 增益误差 分段积分 周期性振荡

0 引言

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)相电流测量在矢量控制算法中扮演着重要角色，其检测是否准确直接关系到电机驱动器的控制性能[1]。然而电机实际相电流经过采样调理环节之后难免会存在偏移误差和增益误差，引起转矩和转速脉动，严重影响电机稳态调速性能，测量误差不仅影响动态性能还影响稳态性能。因此，研究相电流测量误差及其补偿策略有利于提高PMSM的调速性能。

一般情况下，转速脉动可通过高增益的转速调节器得到抑制，但在电梯或牵引驱动器中，为保证乘客的舒适性，转速调节器增益不能太大[2]，因此需寻求其他策略减小测量误差带来的转速脉动。

近年来，为减小电流测量误差，抑制转矩和转速脉动，研究学者对减小电流测量误差进行了研究。可以简单地通过读取静态条件下逆变器的直流偏置来减小偏移误差[3]，然而该方法不能补偿增益误差，且偏移误差在电机运行过程中动态变化时不能完全补偿。文献[4]通过监测直流母线电流中的交流分量可以得到偏移误差，但不能测量增益误差，且需要在直流母线上串接额外的电流传感器。文献[5，6]建立系统模型，通过修改转速调节器输出的转矩电流给定值对电流测量误差带来的转矩、转速脉动进行抑制，但该方法需要精确的电机参数，当电机参数变化或不准确时，补偿器可能出现不稳定。文献[7]采用高频信号注入策略，但该策略会带来附加损耗和噪声。文献[8，9]采用自适应滑模控制器有效减小了转矩脉动，但并不能补偿电流测量本身带来的误差。文献[10]研究了增益误差的影响，提出了一种误差补偿策略，但该方法是针对3个电流传感器检测的情况，并不能应用于采用两个电流传感器进行相电流检测的情况。文献[11]采用一种简单的谐振式观测器对低定子频率下存在的电流测量误差进行补偿，并且采用残余误差补偿器对残余误差进行了补偿以精确观测磁链。文献[12]将电流调节器的输出作为参考电压值进行误差补偿。

本文针对PMSM中采用两个电流传感器进行相电流检测过程存在的测量误差进行了研究，分析了电流测量误差产生原理及其对闭环系统调速性能的影响。为减小转矩和转速脉动，提出了一种对d轴电流分段积分的电流测量误差补偿策略，该方法不受电机参数和运行转速的影响，能有效减小测量误差引起的转矩和转速脉动。

1 相电流测量误差分析

在PMSM控制系统中，参与运算的三相电流通过电流传感器采样，并利用运算放大器进行幅值调节，再经过A-D转换器输入到DSP控制器，相电流检测过程如图1所示。电流传感器的非线性、调理电路的热漂移、A-D转换器的量化误差及各相电流的不平衡都会导致电流测量过程出现误差。

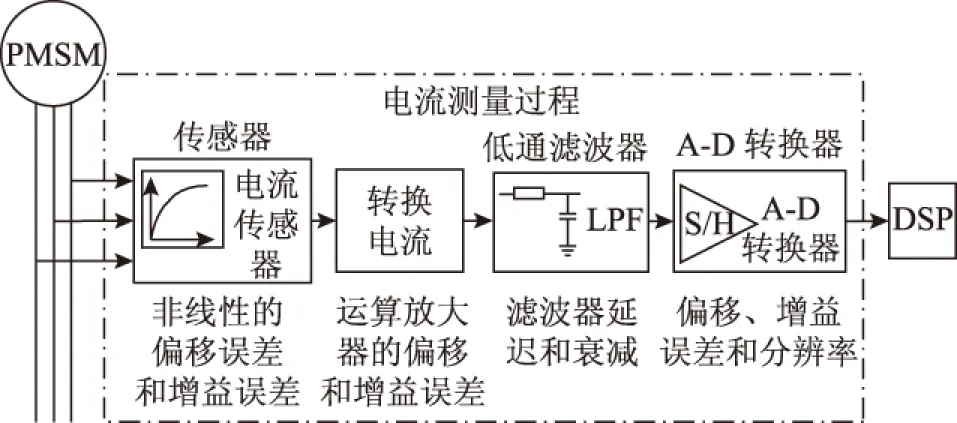
图1 相电流检测过程Fig.1 The measurement path of rotor phase current

相电流测量误差可以分为增益误差和偏移误差两类。增益误差是在相电流处理过程中，比例增益不相等引起的，包括电流传感器、运算放大器和测量电路中无源元件的误差；而偏移误差是由电流传感器、运算放大器和A-D转换器的漂移和残留造成的，它是一个叠加量[13-15]。因此，考虑误差时的相电流测量值可表示为

(1)

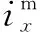
因此，x相的电流测量值与实际值误差可表示为

(2)

由式(1)、式(2)可得

(3)

一般只检测PMSM三相电流中的两相，假设为A相和B相电流，则C相电流可表示为

(4)

(5)

式中，id、iq为d、q轴的实际电流；Δid、Δiq为误差值，由Clarke变换和Park变换可得

(6)

Δid、Δiq不仅与Δia、Δib有关，还与电机电角度θe有关，将式(6)展开可得

(7)

式中，θe=2πfet。

1.1 偏移误差

当电机相电流测量值中包含偏移误差时，有

(8)

将式(8)代入式(7)，可得

(9)

其中

(10)

在dq坐标系下的电磁转矩方程为

(11)

将式(9)代入式(11)，可得

ΔTl=

(12)

由此可见，偏移误差使得闭环控制系统的电磁转矩中包含ΔTl分量，由于ΔTl在fe频率处振荡，使得电磁转矩也在fe频率处振荡。

1.2 增益误差

当电机相电流测量值中包含增益误差时，有

(13)

(14)

由式(7)、式(14)可得

(15)

由式(11)、式(15)可得

(16)

由此可见，增益误差使得闭环控制系统的电磁转矩在2fe频率处振荡。

1.3 测量误差对闭环系统的影响

图2为永磁同步电机矢量控制系统转速环模型，ΔTl作为负载扰动转矩，可得扰动作用下的闭环传递函数为

(17)

图2 PMSM转速环模型Fig.2 Speed loop model of PMSM

为满足系统无静差和抗干扰性要求，转速环采用PI调节器，将系统校正为Ⅱ型系统。因此，式(17)可写为

(18)

式中，kωp、kωi分别为转速调节器的比例、积分系数。由此可得频率响应如图3所示。

图3 频率响应Fig.3 The frequency response

图3表明低频时的转矩脉动可以通过转速调节器进行调节，而高频时的脉动可以由电机转动惯量滤除。最大转速脉动量为

(19)

2 相电流测量误差补偿策略

2.1 测量误差计算

d轴电流经过积分调节器后，其输出为

(20)

式(20)中的d轴测量误差Δid为式(9)和式(15)之和。

由式(9)、式(15)、式(20)可以看出，d轴电流的脉动量中包含fe、2fe频率处的脉动量，因此本文选择iout的积分区间为[0，2π]，如图4所示，iout的积分是一个恒定值，即偏移误差和增益误差。

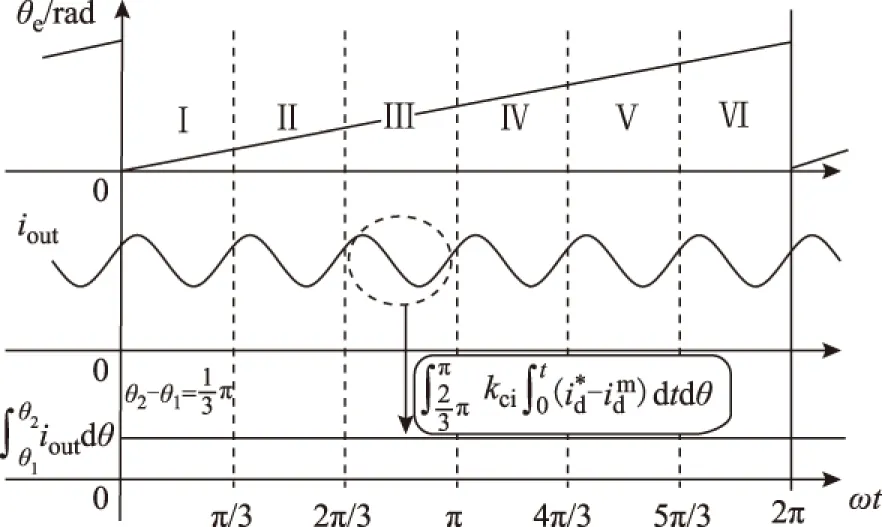
图4 积分区间选择Fig.4 The selection of integral interval

2.1.1 偏移误差计算

对于偏移误差，需要计算A相和B相的偏移误差，图5为误差计算结果。

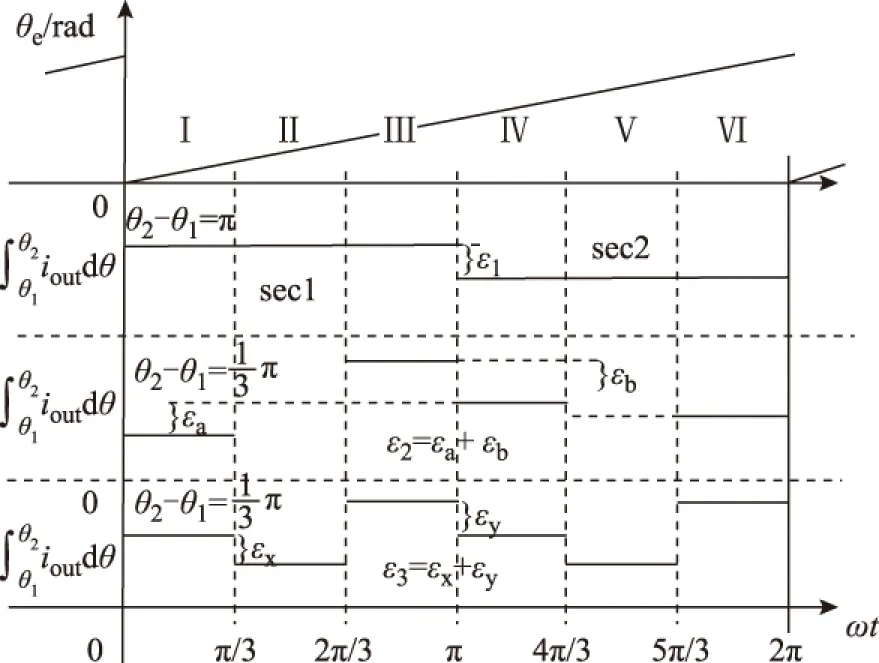
图5 误差计算结果Fig.5 Error calculation results

对式(20)进行积分，积分区间选择每π个电角度，则有

(21)

(22)

将式(21)、式(22)相减，可得

(23)

控制式(23)为零，即可消除A相偏移误差对相电流测量结果的影响。

对式(20)进行积分，积分区间选择每π/3个电角度，则有

(24)

由式(24)可得

(25)

同理，控制式(25)为零，即可消除B相偏移误差对相电流测量结果的影响。

当偏移误差为零时，则对式(20)每π/3个电角度积分的结果满足式(26)。

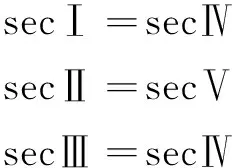
(26)

2.1.2 增益误差计算

当Ka与Kb相等时，式(15)为零，即dq轴不存在增益误差。因此，当Ka与Kb不相等时，式(27)可反映

增益误差。

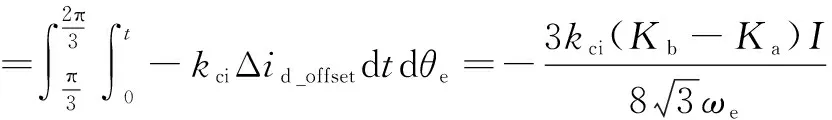
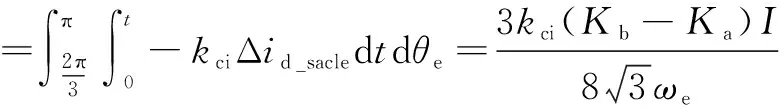
(27)

由式(27)可得

(28)

2.2 相电流补偿

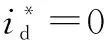
图6 误差补偿算法Fig.6 Error compensation algorithm

3 仿真与实验

3.1 仿真验证

在Matlab2013/Simulink环境下进行系统仿真，电机仿真模型中参数设置参照实际电机参数，见表1。

为分析电流检测中的测量误差对闭环系统的影响，对闭环系统进行仿真分析。仿真条件为：Ka=1.1，Kb=0.9，ia_offset=0.05 A，ib_offset=0.02 A，由式(9)和式(15)可得Δid、Δiq的幅值为1.75 A，给定转速600 r/min，负载转矩5 N·m。

表1 永磁同步电机参数

Tab.1 The parameters of the PMSM

参数数值参数数值额定功率PN/kW1.5额定转速nN/(r/min)3000额定电流IN/A6.0极对数Pn4最大电流Imax/A18.0转动惯量J/(kg·m2)0.915×10-3额定转矩TN/(N·m)5相绕组电阻/Ω0.567最大转矩Tmax/(N·m)15相绕组电感/mH2.316机械时间常数TM/ms2.24电气时间常数/ms4.058

图7 有测量误差时d、q轴和三相电流测量值Fig.7 The measurement value of d，q axis，three-phase current with measurement error

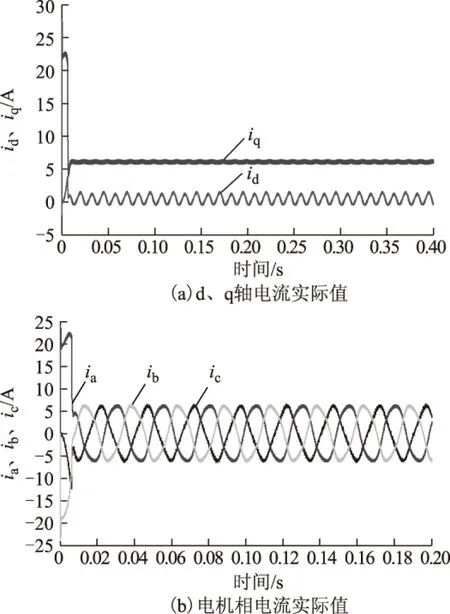
图8 有测量误差时d、q轴和三相电流实际值Fig.8 The real value of d，q axis，three-phase current with measurement error

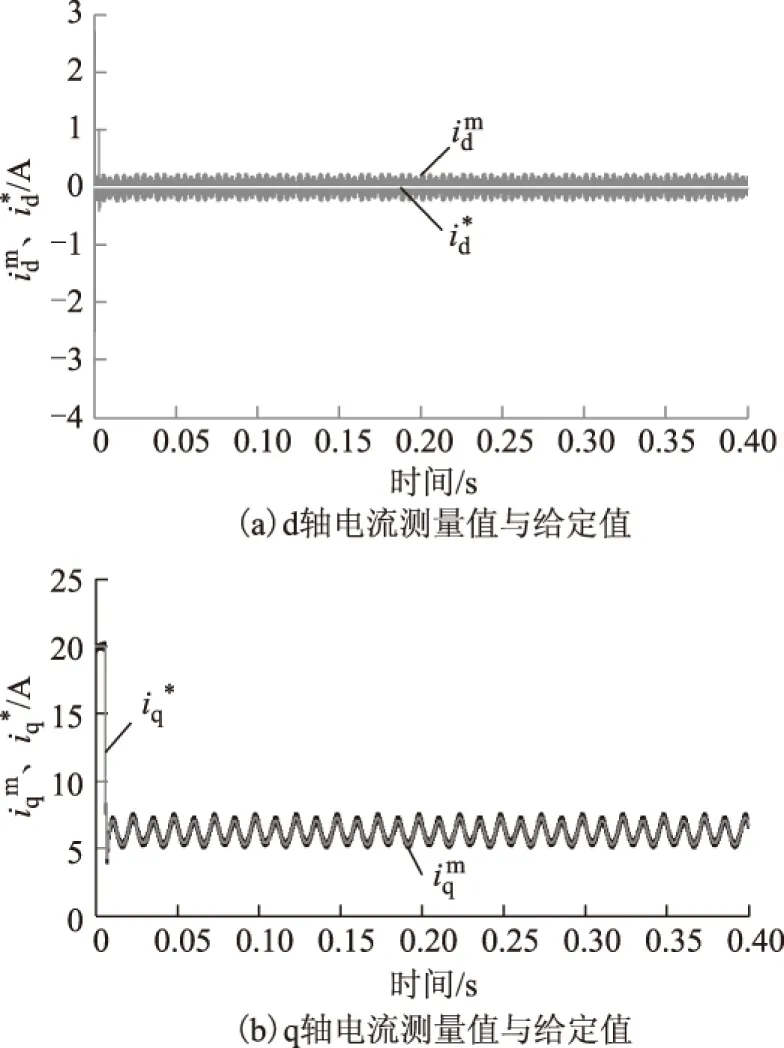
图9 d、q轴电流给定与反馈Fig.9 The given d，q axis current and its feedback

为分析测量误差对闭环系统性能的影响，对稳态时的电机转速进行了FFT分析，仿真结果如图10所示。由式(19)可以看出，电机转速脉动量与Δid呈正比，由于测量误差的影响，使Δid在fe、2fe处振荡，则电机转速也在fe、2fe处振荡，所以图10b所示的稳态时转速FFT分析结果中含有1次和2次谐波，与理论分析一致。

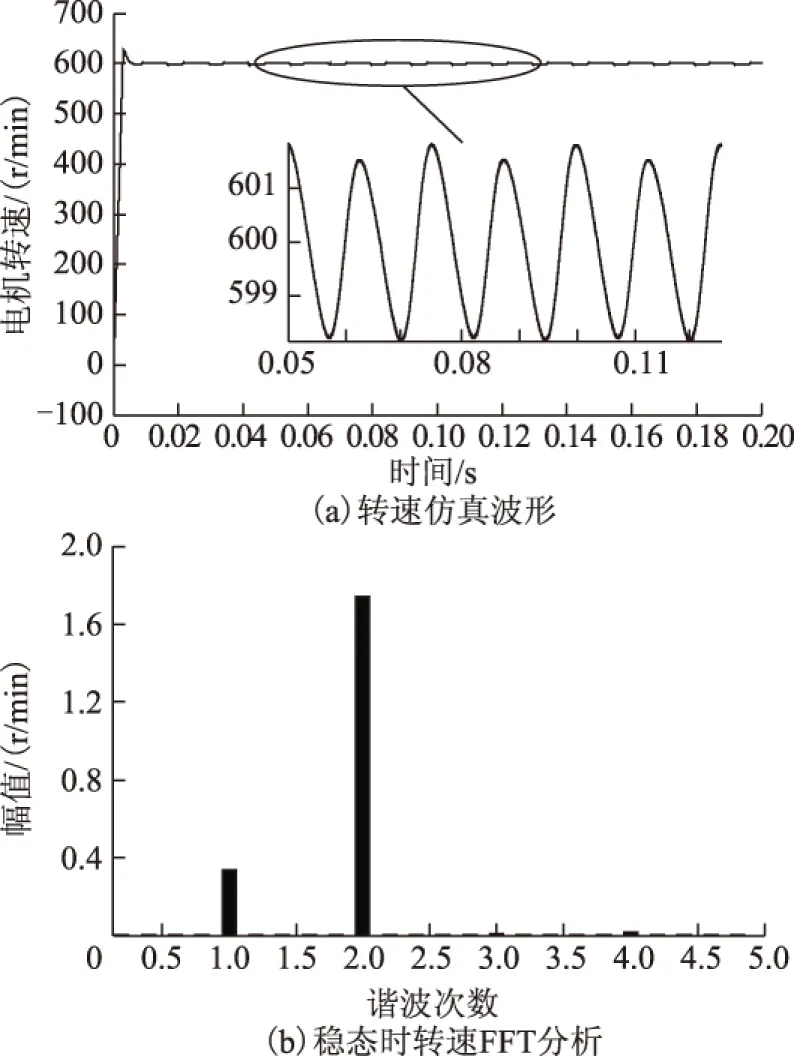
图10 电机转速与FFT分析Fig.10 Motor speed and its FFT analysis

图11为测量误差仿真结果。随着电机运行，测量误差和增益误差趋于一个稳定值，增益误差Ka收敛于1.1，Kb收敛于0.9，偏移误差ia_offset收敛于0.05，ib_offset收敛于0.02，与仿真条件设置一致，说明采用对d轴进行分段积分的测量误差计算方法正确。

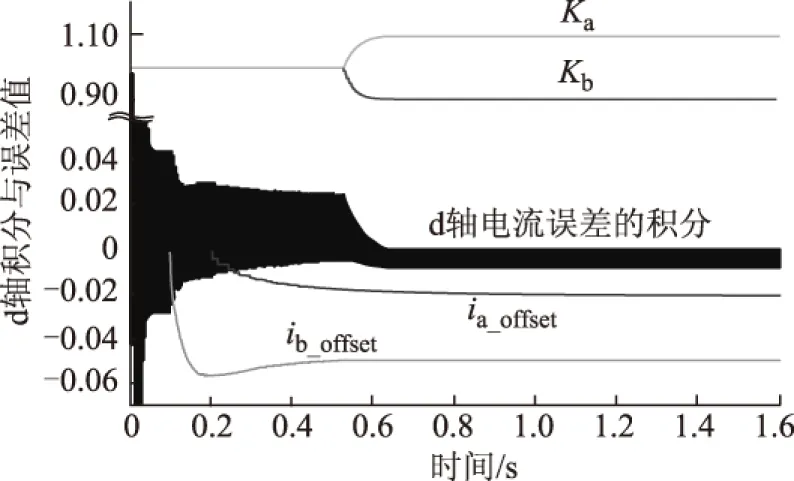
图11 测量误差仿真分析Fig.11 Simulation analysis of measurement error

3.2 实验验证

为进一步验证本文提出的相电流测量误差补偿算法的有效性，搭建基于TMS320F2812DSP芯片的永磁同步电机控制系统，如图12所示。

图12 永磁同步电机控制系统Fig.12 The PMSM control system

图13 有测量误差时电流波形Fig.13 The current waveform with measurement error

采用误差补偿策略之后，d、q轴和A相测量电流与转速波形如图14所示。由图14可见，补偿测量误差之后，系统控制性能提高，稳态时转速未见明显脉动，d、q轴电流基本为恒值，A相电流较为正弦。说明了补偿电流测量偏执的重要性，尤其是在轻载，电机电流较小时，即使较小的偏差也会给系统带来一定不稳定。

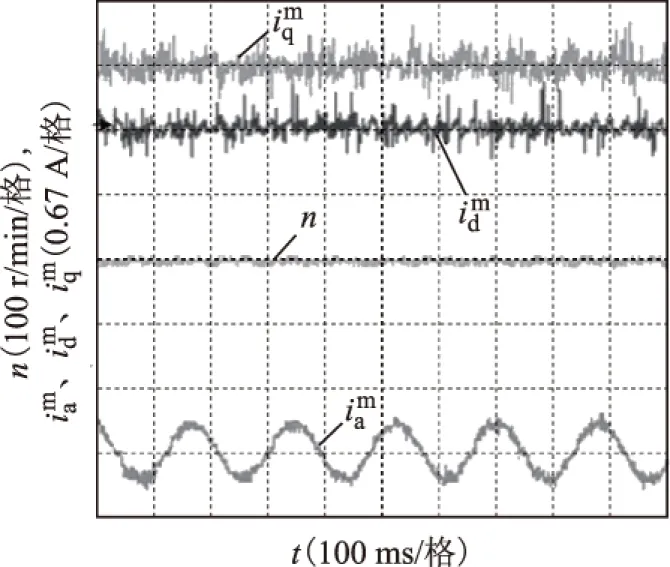
图14 补偿后转速实验波形Fig.14 The speed waveform after compensation

为分析误差补偿策略对电机动态性能的影响，得到误差补偿过程中电机转速的实验波形如图15所示。由此可见，在误差补偿过程中，电机转速脉动量逐渐减小，电机转速趋于稳定值。

图15 误差动态补偿过程Fig.15 Error dynamic compensation process

将本文提出的误差补偿策略应用于其他参数的PMSM控制系统，补偿效果明显，说明基于d轴电流分段积分的补偿策略具有较好的鲁棒性。

4 结论

本文对电机相电流检测中的测量误差进行了分析，研究了增益误差和偏移误差对闭环系统的影响，为减小测量误差对电机控制的影响，提出了一种对d轴电流进行分段积分的补偿策略，仿真和实验结果表明了误差补偿策略的有效性，可以很好地减小测量误差对系统的影响，从而减小转矩和转速的周期性脉动。

[1] 乔鸣忠，夏益辉，朱鹏，等.基于电流闭环和死区补偿的变频驱动调速系统低频振荡抑制[J].电工技术学报，2014，29(11)：126-133. Qiao Mingzhong，Xia Yihui，Zhu Peng，et al.Low-frequency oscillation restrain method of induction motor fed by inverter based on current close-loop and dead-time compensation[J].Transactions of China Electrotechnical Society，2014，29(11)：126-133.

[2] 郭希铮，游小杰，徐从谦，等.大功率电力牵引控制系统硬件在回路实时仿真[J].电工技术学报，2012，27(4)：65-70. Guo Xizheng，You Xiaojie，Xu Congqian，et al.Simulation of hardware in loop for high-power electrical traction system[J].Transactions of China Electrotechnical Society，2012，27(4)：65-70.

[3] 吴楠，李尚盛，查晓明.改进的同步电机阻尼绕组电流观测器[J].电力系统保护与控制，2015，43(1)：67-72. Wu Nan，Li Shangsheng，Zha Xiaoming.Improved Synchronous generator damper current observe[J].Power System Protection and Control，2015，43(1)：67-72.

[4] Kang Y C，Zheng T Y，Kim Y H，et al.Development of a compensation algorithm for a measurement current transformer[J].IET Generation Transmission & Distribution，2011，5(5)：531-539.

[5] Chung D W，Sul S K.Analysis and compensation of current measurement error in vector controlled AC motor drives[J].IEEE Transactions on Industry Applications，1998，34(2)：340-345.

[6] Lam B H，Panda S K，Xu J X，et al.Torque ripple minimization in PM synchronous motor using iterative learning control[C]//The 25th Annual Conference of the IEEE Industrial Electronics Society，1999，3：1458-1463.

[7] Harke M C，Guerrero J M，Degner M W，et al.Current measurement gain tuning using high-frequency signal injection[J].IEEE Transactions on Industry Applications，2008，44(5)：1578-1586.

[8] Samitha Ransara H K，Madawala U K.A torque ripple compensation technique for a low-cost brushless DC motor drive[J].IEEE Transactions on Industrial Electronics，2015，62(10)：6171-6182.

[9] Sencer B，Shamoto E.Effective torque ripple compensation in feed drive systems based on the adaptive sliding-mode controller[J].IEEE Transactions on Mechatronics，2014，19(6)：1764-1772.

[10]Harke M C，Lorenz R D.The spatial effect and compensation of current sensor gain deviation for three-phase three-wire systems[J].IEEE Transactions on Industry Applications，2008，44(4)：1181-1189.

[11]贾学瑞，粟时平，刘桂英，等.并网逆变器死区效应消去补偿方法研究[J].电力系统保护与控制，2016，44(5)：30-35. Jia Xuerui，Su Shiping，Liu Guiying，et al.A novel strategy of dead-time elimination and compensation for grid-tied inverters[J].Power System Protection and Control，2016，44(5)：30-35.

[12]Kim M，Sul S K，Lee J.Compensation of current measurement error for current-controlled PMSM drives[J].IEEE Transactions on Industry Applications，2012，50(5)：3365-3373.

[13]汤浩.一种单相谐波电流实时综合检测算法[J].电气技术，2015，16(3)：52-56. Tang Hao.Integrated real-time single phase harmonic current detection algorithm[J].Electrical Engineering，2015，16(3)：52-56.

[14]陈斌，王婷，吕征宇，等.电压型逆变器非线性的分析及补偿[J].电工技术学报，2014，29(6)：24-30. Chen Bin，Wang Ting，Lü Zhengyu，et al.The analysis and compensation of voltage source inverter nonlinearity[J].Transactions of China Electrotechnical Society，2014，29(6)：24-30.

[15]肖海峰，刘海龙，贺昱矅，等.基于电压空间矢量控制 PMSM系统新型死区补偿方法[J].电工技术学报，2013，28(8)：114-119. Xiao Haifeng，Liu Hailong，He Yuyao，et al.Study of a dead-time compensation method for PMSM drive based on voltags space vector control[J].Transactions of China Electrotechnical Society，2013，28(8)：114-119.

蔡志端 男，1978 年生，博士研究生，讲师，研究方向为电机相电流检测、电机控制、故障诊断与容错控制。

E-mai：czddule@zjhu.edu.cn(通信作者)

王培良 男，1963年生，硕士，教授，研究方向智能控制、故障诊断。

E-mail：wpl@zjhu.edu.cn

Measurement Error Analysis and Its Compensation for Phase Current of Permanent Magnet Synchronous Motor

Cai Zhiduan1Wang Peiliang1Xun Qian1Jiang Yuanyuan2Xun Boyang3

(1.School of Engineering Huzhou University Huzhou 313000 China 2.College of Automation Engineering Nanjing University of Aeronautics and Astronautics Nanjing 211106 China 3.College of Mechanical and Electrical Engineering Inner Mongolia Agriculture University Huhhot 010018 China)

For permanent magnet synchronous motor，to reduce the measurement error of the phase current and meet the speed requirements of high performance，the measurement error analysis and its compensation for the phase current are completed in the paper.Firstly，the principle of the measurement errors is introduced，and the influence of the measurement errors on the performance of the closed-loop speed control system is analyzed.Then，a compensation strategy for the d-axis current in segmented integration is proposed.The d-axis current integration can get the error terms that is used for the compensation of the current measurement.Simulation and experimental results show that offset-errors and gain-errors will cause the oscillation of the torque and the speed with 1 time and 2 times angular frequencies.The compensation strategy can reduce the measurement errors greatly so as to reduce the periodic oscillation of the torque and the speed.

Measurement error，offset-error，gain-error，segmented integration，periodic oscillation

国家自然科学基金项目(61573137)、浙江省公益技术应用研究计划项目(2016C31115)和湖州市公益性技术应用研究计划项目(2015GZ05)资助。

2016-04-12改稿日期2016-08-19

TM315