基于群Monte Carlo的大气噪声二维模型参数估计*

应文威，张学波，刘旭波，李成军

(1.解放军91635部队，北京 102249；2.解放军91388部队 水声对抗技术重点实验室，广东 湛江 524022)

基于群Monte Carlo的大气噪声二维模型参数估计*

应文威**1，张学波2，刘旭波1，李成军1

(1.解放军91635部队，北京 102249；2.解放军91388部队 水声对抗技术重点实验室，广东 湛江 524022)

为解决多天线最佳接收下的多维非高斯噪声参数估计问题，提出了基于群蒙特卡洛的大气噪声二维模型参数估计方案，通过联合设计蒙特卡洛马尔科夫链和优化重要性重采样算法，实现噪声模型的全局最优参数估计。针对该算法高强度运算需求，在GPU平台上对核心运算作细粒度并行计算处理并优化设计，使运算速度大幅提升，以满足实时处理要求。仿真实验结果表明，该算法迭代收敛快，精度高，各参数估计相对误差普遍小于0.02，最大相对误差可控制在0.05以内，运算速度较传统计算有大幅度的提高，可充分满足低频通信系统中实时计算的要求。

低频通信；非高斯噪声参数估计；二维大气噪声模型；Class A 模型；群蒙特卡洛；并行计算

1 引 言

在传统信号处理中，一般认为噪声服从高斯模型。文献[1]在加性高斯噪声基础上，研究了认知无线电网络中基于波达方向估计的主用户频谱感知模型。文献[2]研究了基于高斯白噪声的二维波达方向估计问题，然而当背景噪声偏离高斯模型时，研究成果将不能较好地适用。在超低频通信系统中，受大气雷电等干扰源的影响，概率密度曲线中尾部下降远比高斯噪声曲线平缓，高幅度信号出现几率大大增加，呈现出较强的非高斯特性，所以基于高斯模型的最优接收机将难以达到最佳性能。文献[3]研究了阴影衰落信道模型下的动态信道分配策略，然而依靠经验选择的信道模型缺乏坚实的物理基础。噪声概率密度函数估计在最优接收机设计中至关重要[4]，很多学者在噪声模型上投入了大量精力[5]。Middleton的Class A模型[6-7]就是一种应用广泛且较为精确的统计物理模型。相比于经验模型，Class A模型具有明确的物理解释，同时还能很好地吻合实际数据。

信号分集技术采用多根天线可以有效地解决信号传播中的多径影响。另外，在潜艇低频通信中，美军潜艇传统上采用拖曳天线接收，它的接收方向图是“8”字形，在与航向垂直的方向上接收能力为零。在拖曳天线上加装磁场天线，形成正交互补便可弥补这一缺陷。因此，多天线接收技术得到广泛重视，但要实现其最佳接收必须要解决多维的噪声建模及参数估计问题。文献[8]提出了基于马尔科夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)方法参数估计器，对多维非高斯噪声模型参数估计进行了研究，但该算法难得到全局最优的结果，而且该方法耗时较长，实时性难以达到工程应用要求。群蒙特卡洛(Population Mentor Carlo,PMC)方法[9-10]是一种高效的蒙特卡洛方法，可以很好地作为MCMC一种替代方案[11]。图形处理单元(Graphics Processing Unit,GPU)并行计算在性能、成本和开发时间较传统的CPU解决方案有显著的优势，在信号处理领域具有广泛的应用空间[12-13]。

本文基于CPU+GPU架构，提出了大气噪声二维模型的PMC参数估计方案。该算法精度高，迭代收敛快，能够实现全局最优估计，同时大大减少了时间，可以满足低频通信系统中实时计算的要求。

2 二维Class A模型

McDonald基于两根天线推导了二维Class A模型[4]。若(x,y)是天线1和天线2接收到的归一化信号，则(x,y)的联合概率密度

(1)

3 PMC参数估计算法设计

PMC方法[9-10]融合了MCMC、重要性采样(Importance Sampling,IS)、重要性重采样(Sampling Importance Resampling,SIR)、粒子系统等多种方法。传统MCMC估计中，如果参数空间中存在多个峰值，则可能由于起始点不同而导致结果也不同，而PMC克服了这一问题。同时，也克服了以往ISR方法中样本退化问题，有效提高了估计器的鲁棒性。

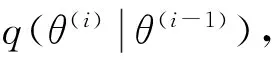
(2)

使θ(i)接受r值，否则θ(i)=θ(i-1)。

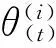
(3)

根据IS原理，在这次迭代中无偏估计器Eπ(h(x))的形式[14]为

(4)

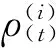
(5)

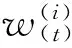
SIR收敛性在O(n-1/2)[15]，对权重方程按式(6)进行优化[16]后，收敛性将达到O(n-1)。

(6)

其中：

为了提升估计器性能，本文设计的PMC算法将采用优化SIR算法。

从式(1)中可知二维Class A模型的待估计参数为θ=(A,Γ1,Γ2,k0,k1)。一般地，π(θ|z)∝f(z|θ)p(θ)，其中z={(xi,yi)|i=1,2,…,N}，p(θ)为先验分布。不失一般性，设p(θ)为平均分布，因此，式(6)变为

(7)

则对于每次迭代，θ(i)的估计为

(8)

不失一般性，设参数(A,Γ1,Γ2,k0,k1)相互独立，于是有

(9)

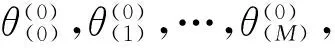
Fori=1,…,T

Fort=1,…,M

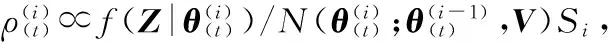
End For

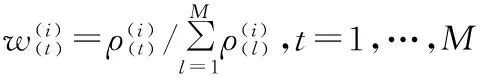
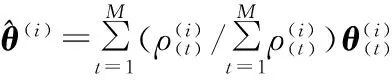
End For

估计参数值

End

其中T代表链长，M代表链数。

4 并行计算设计

通用并行计算架构(Compute Unified Device Architecture,CUDA)采用单指令多线程(Single Instruction Multiple Thread,SIMT)的执行模型，其具体的计算模型由线程、线程块和网格组成，可以实现一维、二维和三维的运算。在实际中，CUDA以线程为基本单位，而线程束(warp)是真正的执行单位，一个wrap由连续的多个线程组成。在同一线程块中，可以通过共享存储器和同步机制实现线程之间的相互通信。一般地，CUDA代码分为主机端代码和设备端内核(kernel)代码，主机端代码主要完成显存分配释放、调用kernel函数等工作，而设备端代码则完成在GPU上执行kernel程序。

在上一节提出的算法中，瓶颈主要在于f(z|θ)的计算，占据了90%以上的运行时间。为了有效缩短时间，将f(z|θ)的计算放在GPU上并行实现。

CUDA是细粒度的并行运算，只有充分考虑底层硬件结构，才能发挥硬件的最大性能，得到高的加速比。可采取以下技术手段：

一是减少GPU和CPU之间的数据传输次数，先将数据集z={(xi,yi)|i=1,2,…,N}从内存上传输到GPU的全局存储器；

二是在CUDA每个线程中，将对应数据从全局存储器中读取到速度最快的寄存器；

三是GPU仅对加法和乘法具有较高的效率，因此CPU预先计算f(xi,yi)的各个参数，得

(10)

这样就避免了减法和除法的运算，大大提高运算效率；

五是为了求和运算中，线程之间能共享数据，将取对数之后的值lnf(xi,yi)存入共享存储器，而对于求和运算，这里采用优化的规约算法进行处理。

图1为一般规约算法，该算法将上次相邻的结果相加，最后实现求和，由于每轮循环都只使用上次循环的一半线程，共需lbN次循环。但该算法在CUDA执行的时候却造成性能上的损失，原因在于读取共享存储器数据时产生块冲突。CUDA将共享存储器分成16个块，数据按顺序从第0块存到第15块，再依次循环。若对共享存储装载满足访问条件时，一次可访问16个存储单元。在一般规约算法中，第一次循环时，第0～15号的线程访问1,3,5,7,9,…,31，形成2路冲突(1-17,3-19,5-21,…,15-32)；第二次循环时第0～15号的线程访问2,6,10,…,62，形成4路冲突(2-18-34-50,6-22-38-54,10-26-42-58,14-30-46-62)，依次类推。可见一般规约算法并没有完全发挥硬件的性能。图2为优化后的规约算法，优化后的算法地址是相邻的，存储单元访问数据时能够有效避免块冲突，从而提升算法效率。

图1 一般规约算法

Fig.1 General reduction algorithm

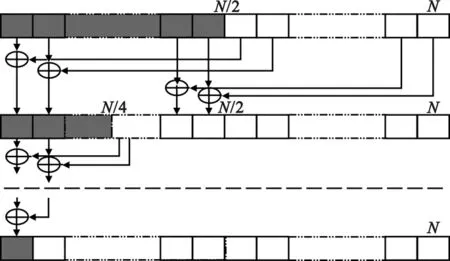
图2 优化后规约算法

Fig.2 Optimized reduction algorithm

5 实验仿真与讨论

为了测试算法性能，设计相应仿真实验，其中实验平台为CPU 为 Intel(R) Xeon(R) x3430，内存2 GB，显卡为NVIDIA GeForce GTX 560。该型显卡配置为：主频1.66 GHz，显存容量1 024 MB，流处理器数量336个，晶体管数目19.5 亿个，计算能力2.1。从式(1)中容易发现，其本质上是多维高斯噪声的混合模型。对于混合模型的随机数生成，可以通过平均分布生成随机数作为标签变量(j=0,1)，再根据标签变量产生相应的多维高斯分布噪声。由于PMC算法的迭代是逐步收敛的，往往在估计时会设置预烧期，通过预烧期之后的数据来进行估计，这样能有效提高估计的精度。因此，本算法参数的估计为

(11)

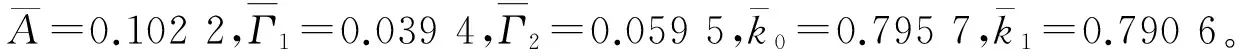
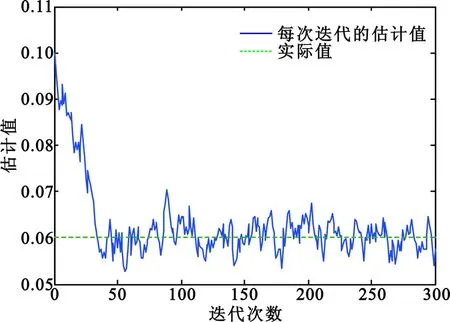
图3 Γ1的迭代收敛情况

Fig.3 The iteration convergence ofΓ1

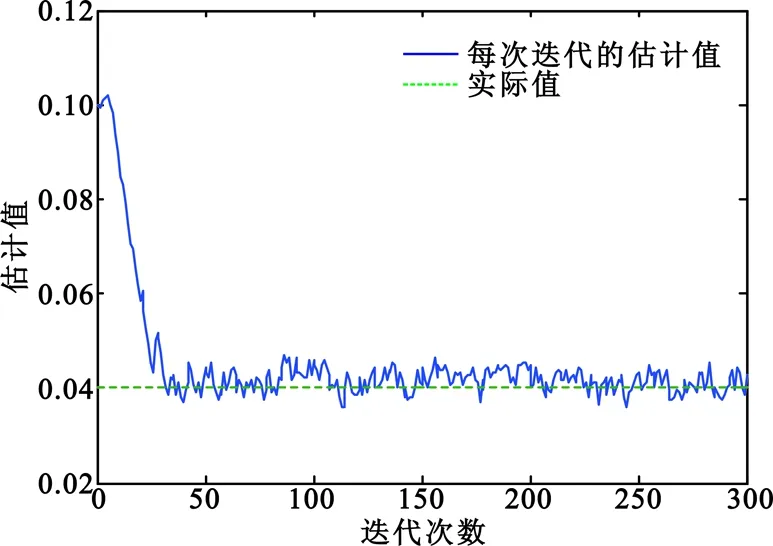
图4 Γ2的迭代收敛情况

Fig.4 The iteration convergence ofΓ2

图5 k1的迭代收敛情况

Fig.5 The iteration convergence ofk1

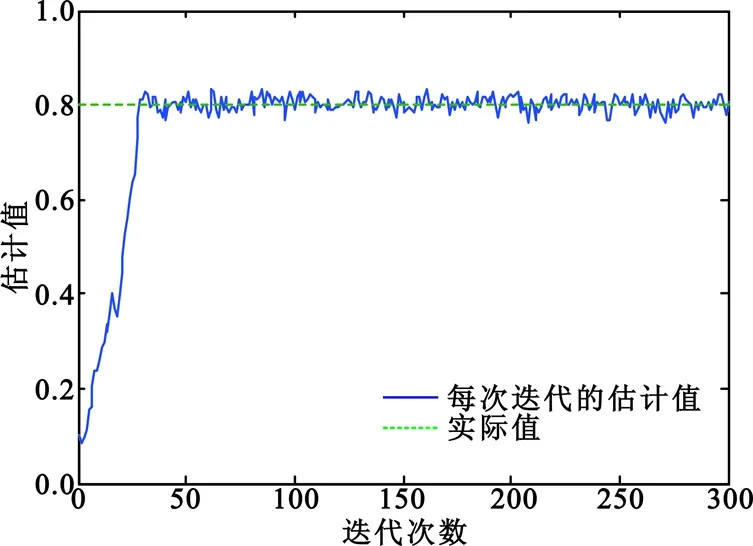
图6 k0的迭代收敛情况

Fig.6 The iteration convergence ofk0

图7 A的迭代收敛情况

Fig.7 The iteration convergence ofA

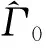
表1 不同Γ0和Γ1的估计结果

Tab.1 Estimation of differentΓ0andΓ1

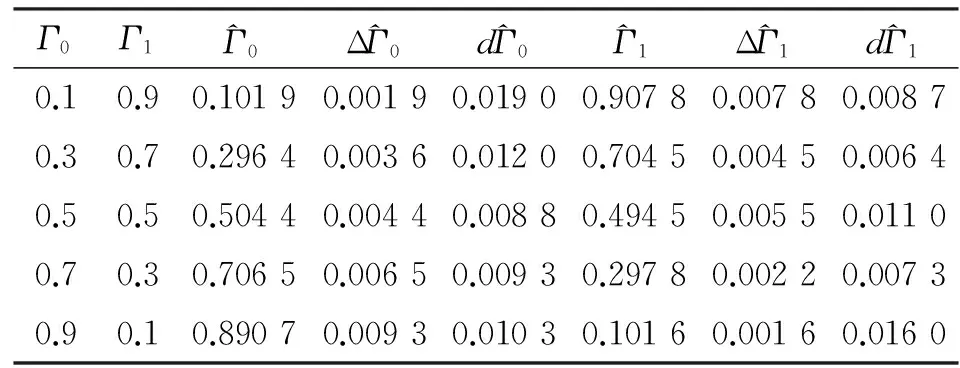
Γ0Γ1^Γ0Δ^Γ0d^Γ0^Γ1Δ^Γ1d^Γ10.10.90.10190.00190.01900.90780.00780.00870.30.70.29640.00360.01200.70450.00450.00640.50.50.50440.00440.00880.49450.00550.01100.70.30.70650.00650.00930.29780.00220.00730.90.10.89070.00930.01030.10160.00160.0160

表2为基于CPU的仿真程序运行时间同基于CPU+GPU仿真程度运行时间的对比。每组数据下，仿真实验运行100次，并对运行时间取平均。

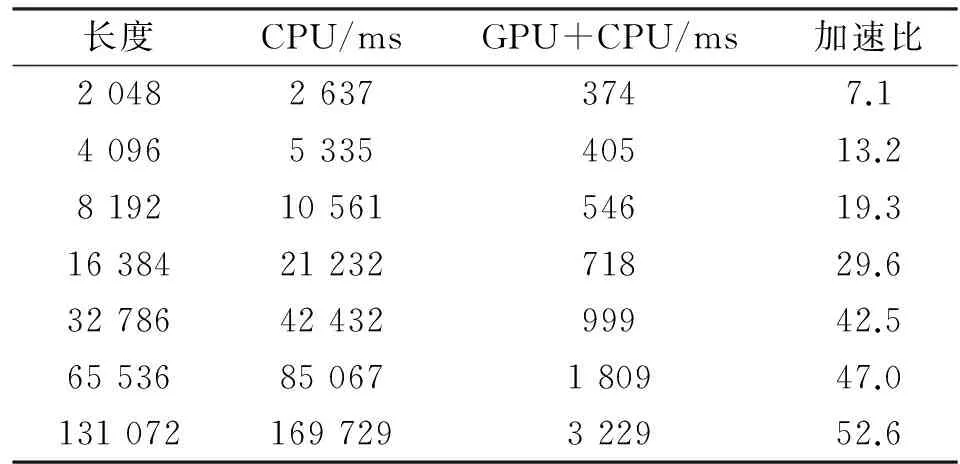
表2 不同平台下算法的运行时间Tab.2 Computation time of the algorithm with different platforms

将表2制成图8和图9，分别为不同架构下的运行时间和加速比的比较。

图8 不同架构下运行时间的比较

Fig.8 Comparisons of the run time in different platforms

图9 噪声数据大小对加速比的影响

Fig.9 The performances of speedup ratio with different noise data sizes

从表2、图8和图9中可以看出，在CPU+GPU 架构下编写的并行算法，其执行时间较串行算法有大幅的缩短。并行程序在数据大小为2 048时，运行时间只需要374 ms，即使在大尺寸数据前提下，也能保持高的运行效率。如在数据尺寸为131 072下并行程序运行时间只需要3 229 ms，而串行程序只有当数据尺寸小于4 096 时才能勉强达到这个指标。从加速比看，随着数据长度的增加，加速比不断提高，即使在测试的最小数据长度(2 048)下加速比也达到了7.1，而当数据长度为131 072 时加速比更达到惊人的52.6 倍！算法的运行时间是该算法是否适用于工程应用的关键指标之一。在CPU 串行程序模式下，运行算法往往要很长时间。这在实际通信系统中，特别是系统需要进行参数实时估计的场合，算法的应用无疑受到了极大的限制，而在CPU+GPU架构的模式下，运行时间则非常短，更易于实际工程应用。目前，接收机的设计倾向于大数据块处理，其原因在于：一方面可以充分利用噪声所提供的信道状态信息；另一方面，从纠错译码的角度考虑，为了提高纠错能力，希望采用较长的交错长度和大约束长度的卷积码。因此，数据运算性能的提升对接收机的性能意义重大。考虑甚低频通信情况下，在接收端，以往受限于计算机处理能力往往采用较低采样率，且需要额外硬件用于专门的数字处理，而若在CPU+GPU 模式下，即使采用高的采样率也完全能够胜任实时参数估计，同时参数估计之后的译码等环节完全能够在计算机上正常处理。最后值得一提的是，本文仿真测试用的GPU 在性能上还只是同类产品中的中低端产品，若使用高端GPU 进行运算，相信会达到更为可观的运行效率和加速比。

6 结束语

因多输入多输出(Multiple-Input Multiple-Output,MIMO)技术优异的性能，越来越广泛地应用于通信系统中。因此，多维非高斯噪声模型参数估计具有重要的意义。但由于多维非高斯噪声模型较为复杂，传统的参数估计方法难以进行全局估计。本文提出了一种基于PMC算法的多维Class A模型参数估计方案，并在CPU+GPU架构基础具体实现，不仅可以实现全局最优估计，还能提高计算效率，满足实时系统的计算。仿真实验结果验证了本文算法的优越性，具有较高的实用价值。在此基础上，可进一步开展对多维非高斯噪声相关接收算法的设计工作，实现高性能多维非高斯接收机。

[1] 任肖丽,高飞飞,王骥,等. 基于DOA 估计的认知无线网络频谱感知[J]. 电讯技术,2016,56(4):353-359. REN Xiaoli,GAO Feifei,WANG Ji,et al. Spectrum sensing based on DOA estimation in cognitive radio networks[J]. Telecommunication Engineering,2016,56(4):353-359.(in Chinese)

[2] 李磊,李国林,路翠华. 高斯白噪声下L阵二维波达方向快速估计[J]. 电讯技术,2014,54(12):1636-1640. LI Lei,LI Guolin,LU Cuihua.Fast estimation of two-dimensional direction-of-arrival based on L-shape array with Gaussian white noise[J]. Telecommunication Engineering,2014,54(12):1636-1640.(in Chinese)

[3] 李航,赵明,王京. 阴影衰落信道下多波束卫星移动通信系统的动态信道分配策略[J]. 电讯技术,2016,56(6):618-623. LI Hang,ZHAO Ming,WANG Jing. A dynamic channel assignment scheme of multi-beam satellite mobile communication system in shadowed fading channel[J]. Telecommunication Engineering,2016,56(6):618-623.(in Chinese)

[4] WANG X,POOR H V. Wireless communication systems:advanced techniques for signal reception [M].London:Prentice Hall PTR,2004.

[5] ABRAHAM D A. Detection-threshold approximation for non-Gaussian backgrounds [J]. IEEE Journal of Oceanic Engineering,2010,35(2):335-341.

[6] CORTES J,SANZ A,ESTOPINAN P,GARCIA J. On the suitability of the Middleton class A noise model for narrowband PLC [C]//Proceedings of 2016 International Symposium on Power Line Communications and its Applications(ISPLC). Bottrop:IEEE,2016:58-63.

[7] BANELLI P. Bayesian estimation of a Gaussian source in Middleton′s Class-A impulsive noise [J]. IEEE Signal Processing Letters,2013,20(10):956-959.

[8] ZHONG J,LIN H. Estimation of two-dimensional Class A noise model parameters by Markov chain Monte Carlo [C]// Proceedings of Computational Advances in Multi-Sensor Adaptive Processing. Virgin Islands：IEEE,2007:12-14.

[9] JOAQUIN M,MARINO I. A nonlinear population Monte Carlo scheme for Bayesian parameter estimation in a stochastic intercellular network model [C]// Proceedings of 6th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing(CAMSAP). Cancun:IEEE,2015:497-500.

[10] EUGENIA K,JOAQUIN M. A population Monte Carlo scheme for computational inference in high dimensional spaces [C]// Proceedings of 2013 International Conference on Acoustics,Speech and Signal Processing. Vancouver:IEEE,2013:6318 -6322.

[11] CELEUX G,Marin J M,Robert C. Iterated importance sampling in missing data problems [J]. Computational Statistics & Data Analysis,2006,50(12):3386-3404.

[12] DULGER O,OGUZTUZUN H,DEMIREKLER M. Implementation of the sampling importance resampling particle filter algorithm in graphics processing unit [C]// Proceedings of 23nd Signal Processing and Communications Applications Conference(SIU). Malatya:IEEE,2015:2195-2198.

[13] ROBERGE V,TARBOUCHI M,LABONTE G. Parallel algorithm on graphics processing unit for harmonic minimization in multilevel inverters [J]. IEEE Transactions on Industrial Informatics,2015,11(3):700-707.

[14] MARIN J M,MENGERSEN K L,ROBERT C P. Bayesian modeling and inference on mixtures of distributions [J]. Handbook of Statistics,2005,25(5):459-507.

[15] HEKTOEN A,HOLDEN L. Bayesian modeling of sequence stratigraphic bounding surfaces [C]// Proceedings of the Fifth International Congress.Wollongong, Australia:IEEE,1996:39-349.

[16] SKARE O,BDLVIKEN E,HOLDEN L. Improved sampling-importance resampling and reduced bias importance sampling [J]. Scandinavian Journal of Statistics,2003,30(4):719-737.

YING Wenwei was born in Zhejiang Province,in 1987. He received the Ph.D. degree in 2013. He is now an engineer. His research concerns atmospheric noise modeling and radio communication.

Email:yingwenwei@sina.com

张学波(1986—)，男，四川人，2014年获博士学位，现为工程师，主要研究方向为水声信号处理、海洋环境噪声建模；

ZHANG Xuebo was born in Sichuan Province,in 1986. He received the Ph.D. degree in 2014. He is now an engineer. His current concerns underwater signal processing and ocean ambient noise modeling.

刘旭波(1983—)，男，黑龙江人，博士，工程师，主要研究方向为无线通信；

LIU Xubo was born in Heilongjiang Province,in 1983. He is now an engineer with the Ph.D. degree. His research concerns radio communication.

李成军(1976—)，男，江苏人，2010年获博士学位，现为高级工程师，主要研究方向为信号处理。

LI Chengjun was born in Jiangsu Province,in 1976.He received the Ph.D. degree in 2010.He is now a senior engineer. His research concerns signal processing.

Parameter Estimation of 2-D Model for Atmospheric Noise Based on Population Monte Carlo Algorithm

YING Wenwei1，ZHANG Xuebo2，LIU Xubo1，LI Chengjun1

(1.Unit 91635 of PLA,Beijing 102249,China;2.Science & Technology on Underwater Acoustic Antagonizing Laboratory,Unit 91388 of PLA,Zhanjiang 524022,China)

In order to solve the problem that includes the parameter estimation of the multi-dimensional non-Gaussian noise model with multi-antenna optimum receiver,a method is proposed to estimate parameters of two-dimensional(2-D) atmospheric noise model based on population Monte Carlo(PMC). Both the Markov chain Monte Carlo algorithm and optimized sampling importance resampling method are used to achieve the global optimal parameter estimation of the multi-dimensional non-Gaussian noise model. Besides,the corresponding algorithm is designed.In consideration of the algorithm requirement for low computational complexity,core computation is designed for fine grain parallelization based on the graphics processing unit(GPU). It improves the algorithm efficiency greatly,and can satisfy the need for real-time processing. The simulation results show that the presented algorithm possesses the characteristics of high precision and fast convergent iteration. The relative error is generally smaller than 0.02,and the maximum relative error is smaller than 0.05. Compared with traditional computing method,the presented method can improve the computing efficiency greatly. And it can fully satisfy the real-time computation in low frequency communication systems.

low frequency communication;non-Gaussion noise parameter estimation;2-D atmospheric noise model；Class A model；population Mentor Carlo；parallel computing

10.3969/j.issn.1001-893x.2016.12.009

应文威，张学波，刘旭波，等.基于群Monte Carlo的大气噪声二维模型参数估计[J].电讯技术，2016,56(12):1352-1358.[YING Wenwei，ZHANG Xuebo，LIU Xubo，et al.Parameter estimation of 2-D model for atmospheric noise based on population Monte Carlo algorithm[J].Telecommunication Engineering,2016,56(12):1352-1358.]

2016-03-30；

2016-07-18 Received date:2016-03-30；Revised date：2016-07-18

国家自然科学基金资助项目(41304015)；装备预研基金项目(9140C290401150C29132)

Foundation Item:The National Natural Science Foundation of China(No.41304015);The Advanced Research Foundation of Equipment(9140C290401150C29132)

TN911.22

A

1001-893X(2016)12-1352-07

应文威(1987—)，男，浙江人，2013年获博士学位，现为工程师，主要研究方向为大气噪声建模、无线通信；

**通信作者：yingwenwei@sina.com Corresponding author：yingwenwei@sina.com