星敏数据转换为参考系欧拉角姿态的方法*
淡 鹏,王 丹,郭延臣
(1.宇航动力学国家重点实验室,西安 710043;2.西安卫星测控中心,西安 710043)
星敏数据转换为参考系欧拉角姿态的方法*
淡 鹏**1,2,王 丹2,郭延臣2
(1.宇航动力学国家重点实验室,西安 710043;2.西安卫星测控中心,西安 710043)
针对三轴稳定卫星星敏感器姿态测量数据转换参考系欧拉角姿态计算的相关问题,首先,系统地总结了转换计算的方法,给出了星敏数据计算姿态矩阵及姿态矩阵解算欧拉角的方法;然后,对工程上常用的312及321转序,从编程角度提出了一种全角度欧拉角解算及值选择方法;最后,分析了采用所提方法转换计算中的常见误差因素及注意事项,并基于分析结果给出了同步星的转序选取建议。研究结果表明所提方法是有效的,对卫星姿态确定和误差分析有一定的参考意义。
三轴稳定卫星;卫星姿态控制;星敏感器;欧拉角解算
1 引 言
卫星姿态[1-2]确定是卫星控制的基础之一,在卫星运行状态计算中有着重要意义。在当前的地球同步卫星中,星敏感器[3-4]已经越来越多的应用在了卫星姿态确定中,相较于传统的红外地球敏感器、陀螺和太阳敏感器组成的定姿系统,其定姿精度有了较大提高。星敏定姿基本原理是通过测量恒星的方位及亮度信息,利用星历表确定其在惯性系下的方位,进而解算出惯性系下的卫星姿态,因此,卫星遥测下传的星敏姿态计算输出常常是测量系相对惯性系的四元数[5-6],这种姿态表示形式相较于传统的欧拉角[7]形式,直观性要稍差一些,原先的欧拉角姿态更容易被人理解。
在地球同步卫星转移段测控的工程计算中,为了理解的方便,常常需要将星敏姿态测量数据转换为参考系下的欧拉角形式。但是,四元数与欧拉角两种表示形式之间并不存在一一对应的关系,转移轨道段可能存在的大角度机动使得不同转序结果可能有较大差异甚至转换异常,这些问题给转换计算带来了困难。一些文献对此进行了研究[1-2,5,8],但大多只是限定角度范围内的方法,且很少有文献涉及转换误差影响因素方面的分析及转换方法的系统阐述。为此,本文对星敏感器姿态测量数据转换为参考系欧拉角姿态的方法进行了较系统地总结,给出了单星敏及双矢量法计算姿态矩阵,以及312和321转序下的一种方便工程应用的欧拉角解算和解选择方法,然后对转换计算中误差产生的主要因素进行了分析,给出了转换的注意事项和一些建议。
2 姿态参考坐标系
在工程上,对三轴稳定卫星[5]姿态的计算常采用卫星本体坐标系相对卫星轨道坐标系、卫星东南坐标系等参考系下的欧拉角表示。常用的几个坐标系定义如下:
(1)卫星轨道坐标系OXOYOZO
坐标原点为卫星质心,ZO轴指向地心,YO轴指向轨道面负法向,XO与YO、ZO构成右手系。
(2)卫星东南坐标系OXEYEZE
坐标原点为卫星质心,OZE轴指向地心,OXE轴垂直OZE指向正东,OYE轴垂直OZE指向正南。
(3)卫星本体坐标系OXBYBZB
原点为卫星质心,三轴分别为卫星的惯量主轴。
(4)J2000地心惯性系
X轴指向J2000平春分点,Z轴为J2000平赤道面法向。
3 星敏姿态转换到参考系的方法
由卫星遥测输出的星敏姿态测量数据计算参考系欧拉角姿态的过程主要包括两部分,即由星敏测量数据计算姿态矩阵和由姿态矩阵解算参考系欧拉角。
3.1 星敏数据计算姿态矩阵
对星敏数据计算姿态矩阵,可使用单星敏的四元数姿态输出计算,也可使用单星敏的两个轴(矢量)测量值或双星敏的各一个轴(矢量)进行双矢量定姿计算。
3.1.1 单星敏数据几何法计算姿态矩阵
对于某单个星敏,设星敏测得的星敏感器坐标系相对惯性系的姿态四元数为q0、q1、q2、q3,其中q0为四元数的标部,q1、q2、q3为矢部。据此可得到惯性系到星敏测量坐标系的转换矩阵(方向余弦阵)为
(1)
同时,由预先测得的星敏感器的安装几何可计算出本体系相对于惯性系的姿态矩阵。设星敏测量系的X轴(星敏横轴)、Y轴、Z轴(星敏光轴)三轴在卫星本体系下的方向矢量分别为Sx、Sy、Sz,则可得到卫星本体系到星敏测量系的转换矩阵(定义为星敏的安装矩阵)为
当参考系建立在卫星东南坐标系或轨道系下时,需要根据卫星的当前位置、速度计算惯性系到卫星东南系的转移矩阵MIE或惯性系到轨道系的转移矩阵MIO(计算方法参见文献[1,5]),进而可得到轨道系到本体系转换矩阵
(2)
以及卫星东南系到本体系转换矩阵
(3)
3.1.2 星敏数据的双矢量定姿
若已知星敏的两个矢量在本体系安装方向及测量值,也可使用双矢量定姿方法进行计算。设测量得到的星敏两个轴在惯性系下的单位矢量分别为V1i、V2i,则由这两个测量值可建立一个正交坐标系
其中:
设星敏的这两个矢量在本体系下安装向量分别为V1b、V2b,同样也可由这两个向量建立一个正交坐标系
其中:
需要说明的是,此方法对单星敏上的双矢量及双星敏各一个矢量组成的双矢量情况均适用,也就是说可使用某单星敏的两个轴(如光轴与横轴)的矢量值进行计算;当有双星敏数据时,也可使用两个星敏的各一个轴(如光轴,可选取精度较好的一个轴)进行双矢量定姿,此时只需要保证两个矢量在本体系下不共线即可(可建立一个正交坐标系)。
3.2 姿态矩阵解算参考系欧拉角
从姿态参考系下的卫星姿态方向余弦矩阵解算三轴欧拉角时,其解算结果与转序有关,工程上对三轴稳定卫星常采用312转序或321转序来确定欧拉角。考虑到转移轨道段姿态存在大范围机动,下面给出一种全角度值域下的计算方法。
3.2.1 基于编程思路的一种全角度欧拉角计算方法
定义绕Z轴旋转角度为偏航角(ψ),绕Y轴为俯仰角(θ),绕X轴为滚动角(φ),则采用312转序时,姿态余弦矩阵为
(4)
当采用321转序时,姿态余弦矩阵为
(5)

为此,借助于C++语言中提供的反正切函数arctan2(y,x)(值域[-π,π])以及反正弦函数arcsin(x)(值域[-π/2,π/2]),从编程角度出发,给出一种对321及312转序均适用的全角度欧拉角计算方法。
对312转序,由式(1)可得欧拉角解为
(6)
注意:式中arctan2为函数,此处的2不是2倍意思。当φ取±π/2时,arctan2的两个入参都为0,此时,θ及ψ的计算结果可能会破坏前后的连续性,这种情况下根据需要可将其值赋值为上一帧计算值,以使得姿态角连续。
分析该解的形式及式(4),发现该解给出的3个欧拉角值域为:φ是[-π/2,π/2],而θ与ψ是[-π,π],即对滚动角还不是全角度值域。但对三轴稳定卫星在多数常用姿态模式下,3个欧拉角满足此范围限定,即可使用该解进行计算。
如果某种模式下,滚动角可以取[-π,π/2)或(π/2,π]时,分析式(4),可给出3个角度值域均为[-π,π]时的解的形式。
记Sign(x)表示x的符号函数,其取值为
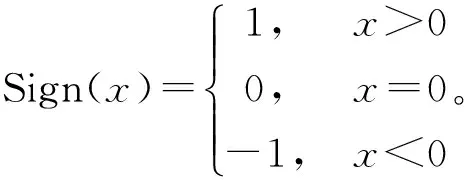
则由式(4)可解出
或
θ=atan2(-m0,2×Sign(cos(φ)),m2,2×Sign(cos(φ)));
ψ=arctan2(-m1,0×Sign(cos(φ)),m1,1×Sign(cos(φ)))。
从上面解的形式可看出,当φ取±π/2时,arctan2的两个入参均为0时,此时θ与ψ可采用保持上一帧解的形式来解决。
同样,对321转序的全角度欧拉角计算式为
或
φ=arctan2(m1,2×Sign(cos(θ)),m2,2×Sign(cos(θ)));
ψ=arctan2(m0,1×Sign(cos(θ)),m0,0×Sign(cos(θ)))。
同样,在θ取±π/2时,arctan2的两个入参均为0时,可根据需要对φ或ψ赋值为上一帧解。
从上面基于编程角度提出的312转序及321转序下的全角度解形式可得出一个结论,即在全角度值域[-π,π]范围内,矩阵转换为3个欧拉角时一般有两组解(两组解有时相等,此时形式上为一组解)。
另外,312转序下,φ取±π/2时;321转序下,θ取±π/2时,都会出现奇异现象,另两个角实际上可取任意值,此时可采用另两个角取值为上一帧解的方法来保证解的连续性。
3.2.2 全角度值域下的解选择
表1给出了采用上面方法计算的几个不同姿态矩阵的321及312转序下两组解的情况。
表1 312及321转序下两组解示例
Tab.1 Euler angle calculation using 312 & 321 (°)

例子312解1φθψ312解2φθψ321解1φθψ321解2φθψ10.2-0.314.0179.8179.7-166.00.20-0.3013.999-179.800-179.70-166.0020.290.010.0179.8-90.0-170.090.0089.80100.000-90.00090.20-80.00330.025.0120.0150.0-155.0-60.032.5021.47133.120-147.501158.53-46.8740.090.00.2180.0-90.0-179.80.0090.000.2000.00090.000.20
从表1可看出,不同转序下的转角有时差别很大,有些情况下又基本接近甚至相同;同一转序下的两组解有时也会相近或相同。
由于在全角度值域(限定为[-π,π])内,312转序及321转序下通常有两组解,此时需要对其进行取舍。下面给出两种取舍方法:
(1)卫星姿态模式下的值域约束法
当姿态转序限定后,分析其两组欧拉角的情况,两组解的差别主要体现在值域上。为此,可根据卫星当前的姿态模式及其值域进行取舍。
如在地球指向模式(Z轴对地时),俯仰与滚动角一般为小量,据此可选出合理值。
在大推力发动机点火情况下,因某些平台下的卫星发动机安装在本体系的-Z轴,点火时需要俯仰方向转动π/2,而其滚动角一般为小量,此时对312转序可直接使用式(4)求解。
另外,通常情况下,卫星3个欧拉角中某一角度在作大角度范围变化时,另两个角则在小角度范围内变动,此也可以作为选解的先验信息。
(2)通过与目标姿态值的偏差进行取舍
对某限定转序下欧拉角的两组解φ1、θ1、ψ1和φ2、θ2、ψ2,设卫星当前的目标姿态角(或预估姿态角)为φo、θo、ψo,则可分别求出两组解与目标姿态的偏差如下:
此值反映了不同解与目标姿态的接近程度。然后,通过比较这两个偏差值,看哪组偏差值小就可以选取哪组姿态;若两者偏差相同,则可选取任意一组。对仅一个角进行大范围机动的情形,比较时可直接对目标角取为零值,此时可将上面的比较公式简化为
4 转换误差因素
星敏感器定姿相对传统的太敏+地敏等定姿方法来说精度有了较大提高,但是,向参考系欧拉角姿态转换过程中,转换结果的精度容易受到一些因素的影响,如未正确处理,甚至会产生与期望值相差较大的结果。
4.1 星敏安装误差及消除
星敏安装误差是影响定姿结果精度的一种因素。由于星敏感器的安装及加工误差、光学系统的几何畸变以及其他一些因素的影响,地面计算时为了得到更高精度的姿态数据,有时就需要对星敏感器进行标定。
计算时由星敏的地面标定数据可以获得星敏坐标系相对于理论安装之间的补偿矩阵ΔM,令MBS_C=(E+ΔM)·MBS(E为单位阵),并将MBS_C代替卫星本体系到星敏测量系的转换矩阵MBS,即可获得修正后的卫星姿态矩阵。
4.2 卫星位置的影响
星敏定姿结果向参考系转换首先在于计算参考系到本体系转换矩阵。从公式(2)~(3)看出,当使用星敏四元数进行姿态确定时,影响矩阵计算结果的主要因素在于惯性系到参考系的转换矩阵MIO及MIE。
从MIO计算公式可见,其计算值主要受卫星位置及速度矢量方向影响。例如:在位置不变而速度方向变化时会使动量矩改变,进而影响到轨道倾角的计算,同样位置矢量的误差也会对倾角矢量的计算造成影响,这些都会造成MIO的偏差。
从MIE的计算公式可见,其计算值主要受卫星位置矢量的影响。
在卫星变轨期间,若位置速度变化较大,则会直接影响姿态的计算过程,此时需要使用带动力的轨道外推或实时定轨[9-10]结果进行计算。
图1为使用某地球同步卫星转移轨道段某次远地点变轨过程中一个星敏感器实测数据计算的312转序下俯仰角输出随时间变化曲线,分别使用了实测轨道与无动力外推轨道进行卫星位置计算,可发现无动力外推时俯仰角出现明显偏差。
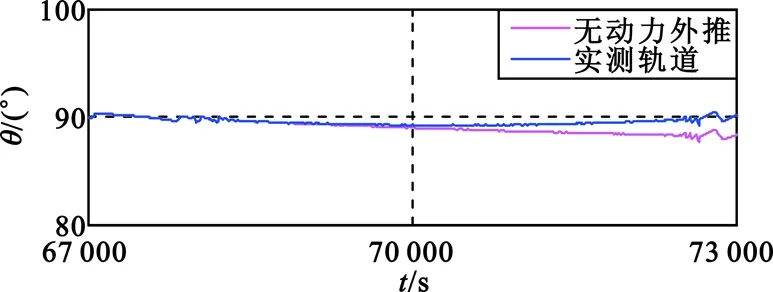
图1 因位置误差导致的点火过程俯仰角偏差曲线
Fig.1 Pitch bias plot because of position error
4.3 转序选择的影响与分析
当卫星三轴姿态欧拉角均为小量时,由式(4)~(5),两种转序下姿态矩阵均可近似为

可见当三轴姿态为小量时,对同一余弦矩阵312与321的解算结果近似。普通的三轴稳定地球同步卫星在定点后,姿态偏差一般情况下为小量,由此可得出结论:定点后小角度偏差时,用312与321转序计算的欧拉角姿态已近似相同。
在同步卫星发射的转移轨道段(星箭分离至定点前),很多情况下姿态角并非小量。从表1可看出,非小角度情形下,对同一姿态余弦矩阵,不同转序解出的欧拉角可能有较大差异。
结合3.2节分析,312转序下,φ取±π/2时;321转序下,θ取±π/2时,欧拉角会出现奇异现象。而某平台卫星在转移轨道段的变轨过程中,常常需要将俯仰角先调整到π/2附近(因490 N发动机安装在-Z面)。设此情形下滚动角为小量,在此限定下给出几组转换结果,如表2所示。
表2 俯仰90°附近两种转序的欧拉角示例
Tab.2 Euler angle conversion when pitch is near 90° and 312 & 321 are adopted (°)
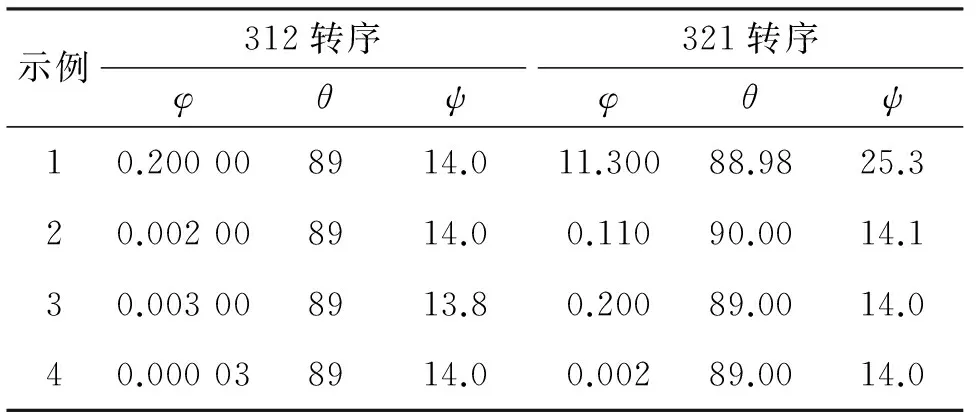
示例312转序φθψ321转序φθψ10.200008914.011.30088.9825.320.002008914.00.11090.0014.130.003008913.80.20089.0014.040.000038914.00.00289.0014.0
在示例1及示例2中,312的φ为小量,但相应的321下的φ却相差较大。
从表2可得出,大角度机动时,对同一余弦矩阵,不同转序下的角度可能有较大差异。因此,必须提前限定好基准转序,谨防转序选择不同导致的计算结果偏差。
5 结束语
本文从工程实际情况出发,对三轴稳定卫星星敏测量数据计算参考系(轨道系或东南系)欧拉角姿态的方法、常见误差影响等进行了较系统地总结和分析。通过本文的计算与分析可得出以下结论:
(1)文中所给定的星敏测量到姿态矩阵的计算、从编程角度提出的一种全角度欧拉角计算及解选择方法等是可行的;
(2)全角度值域下某转序解算的欧拉角有两组(有时可能相同);
(3)姿态转序、卫星位置等因素均会对计算结果造成较大影响,在轨道机动过程中建议使用实时更新的轨道;
(4)同步星定点后的小角度姿态变化时,312与321转序计算结果基本相同;
(5)在转移轨道段,若有俯仰角大范围机动时,建议使用312转序。
应该看到,星敏数据计算参考系姿态的精度还受测量数据的噪声等因素影响,下一步将重点对连续观测数据的滤波方法等进行研究。
[1] 李恒年. 地球静止卫星轨道与共位控制技术[M]. 北京:国防工业出版社,2010:50-54. LI Hengnian. Geostationary satellite orbital analysis and collocation strategies[M]. Beijing:National Defense Industry Press,2010:50-54.(in Chinese)
[2] JING W,XIA X,GAO C,et al. Attitude control for spacecraft with swinging large-scale payload[J]. Chinese Journal of Aeronautics,2011,24(3):309-317.
[3] 钟德安,张同双,冯鸿奎,等. 基于星敏感器的船载雷达误差修正参数解算方法[J]. 电讯技术,2014,54(8):1077-1081. ZHONG Dean,ZHANG Tongshuang,FENG Hongkui,et al. Calculation method of error-correction parameters for ship-borne radar based on star sensor[J]. Telecommunication Engineering,2014,54(8):1077-1081.(in Chinese)
[4] 张同双,钟德安,潘良,等.船用星敏感器姿态测量误差建模与仿真分析[J]. 电讯技术,2014,54(2):218-223. ZHANG Tongshuang,ZHONG Dean,PAN Liang,et al. Modeling and simulation of attitude error model for ship-bore star sensor[J]. Telecommunication Engineering,2014,54(2):218-223.(in Chinese)
[5] 淡鹏,张定波,王丹,等. 三轴稳定卫星姿态可视化绘制与建模[J]. 电子科技,2014,27(5):136-139. DAN Peng,ZHANG Dingbo,WANG Dan,et al. Attitude visualization and modeling of three-axis stabilized satellite[J]. Electronic Science and Technology,2014,27(5):136-139.(in Chinese)
[6] AHMADI M,KHAYATIAN A,KARIMAGHAEE P. Attitude estimation by divided defference filter in quaternion space[J]. Acta Astronautica,2012,75(1):95-107.
[7] 淡鹏. 火箭飞行姿态可视化绘制方法[J]. 弹箭与制导学报,2014,34(2):98-100. DAN Peng. Visualization method of rocket flying attitude[J]. Journal of Projectiles,Rockets,Missiles and Guidance,2014,34(2):98-100.(in Chinese)
[8] 张帆,曹喜滨,邹经湘. 一种新的全角度四元数与欧拉角的转换算法[J]. 南京理工大学学报,2002,26(4):376-380. ZHANG Fan,CAO Xibin,ZOU Jingxiang. A new large-scale transformation algorithm of quaternion to Euler angle[J]. Journal of Nanjing University of Science and Technology,2002,26(4):376-380.(in Chinese)
[9] 淡鹏,李恒年,李志军. 应用三向测量数据的深空探测器实时滤波定位算法[J]. 航天器工程,2015,24(2):21-26. DAN Peng,LI Hengnian,LI Zhijun. Real-time filtering positioning algorithm using three-way measurement data for deep space probe[J].Spacecraft Engineering,2015,24(2):21-26.(in Chinese)
[10] 淡鹏,李恒年,张定波,等. 基于多元非完备信息的实时滤波定轨方法[J]. 飞行力学,2014,32(3):283-288. DAN Peng,LI Hengnian,ZHANG Dingbo,et al. Real-time filtering orbit method based on multiple incomplete observation[J]. Flying Dynamics,2014,32(3):283-288.(in Chinese)
DAN Peng was born in Danfeng,Shaanxi Province,in 1979. He received the M.S. degree in 2005.He is now a senior engineer. His research concerns spacecraft’s data processing and analysis.
Email:danpeng@126.com
王 丹(1980—),女,陕西渭南人,硕士,工程师,主要从事航天器轨道计算工作;
WANG Dan was born in Weinan,Shaanxi Province,in 1980.She is now an engineer with the M.S. degree. Her research concerns satellite orbit calculation.
郭延臣(1981—),男,河南三门峡人,硕士,工程师,主要从事计算机软件方面的研究。
GUO Yanchen was born in Sanmenxia,Henan Province,in 1981.He is now an engineer with the M.S. degree. His research concerns computer software.
Method for Transferring Star Sensor Attitude to Reference Coordinate Euler Angle
DAN Peng1,2,WANG Dan2,GUO Yanchen2
(1. State Key Laboratory of Astronautic Dynamics,Xi′an 710043,China;2. Xi′an Satellite Control Center,Xi′an 710043,China)
The measurement data of star sensor for three-axis stabilized satellites’ attitude often need to be converted to the Euler angle in a reference coordinate system. In view of this,the conversion methods are summarized,including the conversion from star sensor data to attitude matrix and conversion from attitude matrix to the Euler angles. From the programming point of view,a way to calculate full-scale Euler angle is also given under 312&321 transform orders which are often used in project. Then some error factors are analyzed,and the transform order suggested for geostationary satellite is also provided according to analysis.The results indicate that the method is correct and useful for the attitude calculation and error analysis of three-axis stabilized satellites.Key words:three-axis stabilized satellite;satellite attitude control;star sensor;Euler angle calculation
10.3969/j.issn.1001-893x.2016.12.007
淡鹏,王丹,郭延臣.星敏数据转换为参考系欧拉角姿态的方法[J].电讯技术,2016,56(12):1340-1345.[DAN Peng,WANG Dan,GUO Yanchen.Method for transferring star sensor attitude to reference coordinate Euler angle[J].Telecommunication Engineering,2016,56(12):1340-1345.]
2016-03-30;
2016-06-03 Received date:2016-03-30;Revised date:2016-06-03
V412.4
A
1001-893X(2016)12-1340-06

淡 鹏(1979—),男,陕西丹凤人,2005年获硕士学位,现为高级工程师,主要从事航天器数据处理及分析工作;
**通信作者:danpeng@126.com Corresponding author:danpeng@126.com

