一种改进的交通网络路径选择算法

段明义，张 文

(中州大学 信息工程学院，河南 郑州 450044)



一种改进的交通网络路径选择算法

段明义，张 文

(中州大学 信息工程学院，河南 郑州 450044)

运用人工智能领域的启发式搜索方法，以交通网络为研究对象，在深入分析经典Dijkstra最短路径算法的基础上，提出了一个基于启发式的最短路径算法，并证明了该方法的有效性。经过对改进算法仔细分析后，讨论了其改进之处。结合具体应用，从启发函数、搜索范围和排序方法等方面，提出了相应的改进策略，并将其应用到仿真试验中。结果表明：在不同图层下，该算法具有良好的伸缩性；与已有路径选择改进算法相比,在不同路径权值选择下，都能够有效地缩短路径查找时间，从而更好地满足出行需要。同时，也给出了不同地理距离下初始搜索半径的参考值。

智能交通系统；限制搜索区域；启发式方法；交通网络；路径搜索；左倾树

0 引言

实现城市的繁荣、有序和快速发展，一个基本条件是良好的城市交通系统。但随着各城市机动车保有量的不断增加，导致对交通需求的急剧增加，紧接而来的一系列如交通拥堵、交通事故频发、环境污染严重及能源短缺等问题，给人们生产、生活等带来了诸多不便，这些都制约着一个城市的进一步、可持续的发展。出行者在交通出行中，一个经常关心的问题是如何迅速选择一条最优的路径。因此，出行最优路径选择算法问题的研究已迫在眉睫。

求解两点间的最短路径问题，已经有很多学者做了研究，给出了很多的算法，其中以Dijkstra算法[1]最为经典。该算法可以在O(n2)(n为节点数)时间复杂度情况下，求出某初始点到其他与其有路径相通的点之间的最短路径。当节点个数较少时，O(n2)级别的时间复杂度是可以接受的，实际系统中，节点个数往往较多，该级别的复杂度就显得效率低下，因此，直接使用Dijkstra算法的情况不多。

文献[2-3]针对堆排序算法做了分析；文献[2]给出了一种基于左倾树的堆排序改进算法，在输入数据排列任意的情况下，该算法实现排序的时间复杂性为O(nlogn)；通过只对最短路径上节点的临界点处理，在不涉及其他节点的情况下，文献[4]对Dijkstra算法进行优化，使得计算的节点数大幅减少，从而提高了算法的速度；文献[5]讨论了启发式算法在路径规划问题中的一些改进策略，该方法考虑到了一些计算机硬件因素；文献[6]采用预先计算存储的方法，程序运行时，根据初始节点和目标节点，直接调用数据库查询语句，查询出事先计算好的两点间的距离，如果图中节点数目较多，额外存储空间开销就较大。

因此，路径搜索在交通网络中是一个比较复杂的问题，设计算法时，需要考虑多种方面的因素，然后给出最终解决方案。本文将启发式的思想引入Dijkstra算法中，并对搜索区域加以限制，提出限制搜索区域的启发式最短路径算法(Restricted Searching Area Heuristic Shortest Path Algorithm, RSAHSPA)，该算法能够有效缩短路径搜索时间，为使用者提供出行依据。

1 路径搜索算法描述

1.1 寻径问题网络模型

寻径问题是在图论中研究的热点之一，目标是设计一个算法，寻找图中从初始节点到目标节点的一条通路。城市路网除具有一般路网的特点之外，还有其特殊之处：数据量大和结构复杂。这都使得城市路网的结构变得非常复杂，现实中的城市路网实体只有抽象化为图论中的网络图后，才能做最佳路径分析，一般的方法是采用GIS技术生成其对应的电子地图。本文的研究在已生成的电子地图上进行，以此讨论最短路径算法的实现过程。

1.2 Dijkstra寻径算法

定义1 图是由1个顶点集V和1个弧集VR构成的数据结构，Graph=(V,VR)，其中，VR={|v,w∈V∧P(v,w)}，表示从v到w的1条弧，P(v,w)定义了弧的意义或信息，一般设置为该弧的权重[7]。

Dijkstra算法采用贪婪策略，描述如下。

算法1：

(1)初始，从节点集合V′={vs|vs∈V}出发，vs为路径初始节点。

(3)在所有满足vi∈V′∧vj∈M的弧中，选择权重最小的边，设该边在M中依附的节点为vj，若vj=ve(ve为路径目标节点)，则算法结束。

(5)返回(2)。

当图中节点个数很多的时候，Dijkstra算法的性能就显得有些低。此时，为了提高搜索的效率，可以在牺牲一定精确性的情况下达到提高查找速度的目的。启发式算法就是这样一种策略。在每次扩展过程中，尽量选择离最终路径近的那些节点。

1.3 启发式方法

定义2 设评价函数f(vj)=g(vs,vj)+h(vj,ve)[8]，式中，g(vs,vj)为从初始节点vs经过寻径算法到达节点vj的权值之和，且g(vs,vs)=0；h(vj,ve)为节点vj的代价函数，h(ve,ve)=0，它预测从vj到终点ve的代价。一个点是否能被优先选用进行搜索，主要由评价函数f(vj)的值来决定。

引入代价函数h(vj,ve)后，每次对节点的扩散不再是盲目的，而是有方向性的。其值越大，算法的解也就越偏离最优解，但同时时间耗费也越小；其值越小，搜索所花费的时间越大，算法的解也就越逼近最佳解。基于启发式的路径搜索算法如下。

算法2：

(4)返回(1)。

定理1 设有序序列V′={vs,v1,v2,…,vj,…,vn,ve}，j=1,…,n，为使用启发式方法求出的从初始点vs到目标点ve的路径上的点，该路径P′=(vs,v1,v2,…,vj,…,vn,ve)，j=1,…,n，distmin(vk,vl)用来记录节点vk到节点vl最小权值之和，若满足(∀vj)[h(vj,ve)≤distmin(vj,ve)∧(vj∈V′)]，则P′为最短路径。

fp(ve)=gp(vs,ve)+hp(ve,ve)=gp(vs,ve)。

引入记号d(vk,vl)来表示边的权，则：

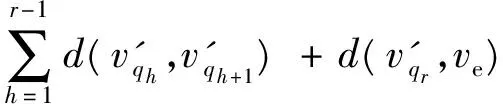
即：

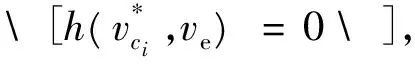
2 算法的改进

2.1 评价函数

评价函数f(vj)的任务主要是用来估计搜索路径上某节点vj的重要性。理论上讲，它可以是任意的函数，具体应用中采用什么样的形式，主要由应用而定。一个节点的价值一般从两方面考虑：搜索到该节点时算法已经付出的代价g(vs,vj); 如果选择从该节点出发到达目标节点ve，算法将要付出的代价h(vj,ve)。 一般来说，已经付出的代价g(vs,vj)的值是一定的，而最关键的就是根据具体应用来选择合适的h(vj,ve)。

在网络地图中，设两点vj和ve的坐标分别为(xj，yj)与(xe，ye)，常用的启发式函数主要有：

曼哈顿距离：h(vj,ve)=(|xj-xe|+|yj-ye|)；

切比雪夫距离：h(vj,ve)=max{|xj-xe|,|yj-ye|}。

其他形式的代价函数也可以选择，只要满足最优解条件即可。欧氏距离代表了两点间的直线距离，是一般情况的首选。在此，考虑到计算机做乘方和开方运算，耗时比加减大很多，故选择曼哈顿距离作为启发函数。

2.2 搜索区域

Dijkstra算法的搜索区域，可近似地看成以初始节点Vs为圆心所构成的一系列同心圆，各个节点依离初始节点的距离远近而先后被搜索到。整个过程没有涉及终点Ve所在的方向或位置，因此，其被搜索到的概率与其他节点Vj是相同的。若图中顶点数目较多，或初始节点Vs与终点Ve间距离较大，算法实际运行效率将大大降低[10-11]。

启发式的搜索方法能够改变这种状况。文献[12]提出了一种矩形限制搜索区域，缩小了搜索的范围，提高了效率。在此基础上，本文将搜索区域进一步缩小，限制在一个条状范围内，如图1所示。以初始节点Vs和终点Ve分别画半径为r(r为搜索半径，该值可调整)的圆，与两圆相切的直线分别为L1和L2，则两直线与两圆围成的条状区域即为搜索区域。

图1 搜索区域示意图Fig.1 Schematic diagram of searching area

实际算法实现时，为了进一步简化计算，可以将搜索区域的横坐标值进一步简化为(xs-r,xe+r)，而纵坐标轴限定在两平行线L1，L2间不变。

初始时，根据经验，设置r值，运行算法，进行搜索，如果搜索到终点，则算法结束，否则，按预设增量增大r值，在一个更大的搜索区域上进行搜索，直至搜索到终点。最坏的情况即是搜索扩展到了整个区域。实际算法中，搜索半径r值设定为一个递增序列ri，形如ri={1, 1.5, 2, 2.5, 3, …}，如果根据前一个半径序列的值没有在搜索区域内找到终点，则选择半径序列中的下一个值来进行搜索。

由于程序首先考虑的是位于条状区域内的点，而不是所有的点，这样就减少了对无用节点的考察，加速了程序的运行。

2.3 排序方法

定义3 堆是满足下列性质的数列{k1,k2,…,kn}：

前者称为小顶堆，后者称为大顶堆[7]。在此主要关注前者，并且采用一种改进的堆结构来进行排序。

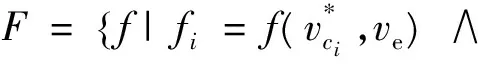
左倾树排序方法是众多排序方法中较快的一种。在原始输入数据任意排列的情况下，该算法的时间复杂度可以达到O(nlog2n)[2]。左倾树实际上就是经典堆结构的一个改进。

定义4 左倾树T是1棵具有特殊性质的二叉树,其中每个结点满足下列性质。

(1)给树中每个节点k赋予1个Ek值：如果该节点具有不多于1个孩子，则Ek=1；如果该节点有两个孩子k1和k2，则Ek=min{Ek1,Ek2}+1。

(2)根节点的值小于(仅考虑小顶堆)以该节点为根的子树上所有节点的值；如果节点k无左孩子，则它必然无右孩子；如果k同时具有两个孩子(分别为k1和k2)，则左孩子节点的Ek值Ek1大于等于右孩子节点的Ek值Ek2。

用左倾树实现排序的过程和普通的堆排序相似，也分为构造和排序两个阶段：第1阶段执行构造过程，输入含有n个节点的待排序序列，经过n-1次左倾树的合并过程，构造1棵新的左倾树；第2阶段执行排序过程，再经过n-1次左倾树的合并过程，从而最终实现排序。

合并过程描述如下(仅考虑两棵树的情况)：

(1)如果有一棵左倾树为空树，合并后的结果为另一棵左倾树。

(2)将根节点值小的左倾树的右子树与另一棵左倾树进行合并，使用合并后的结果代替该右子树。

(3)如果合并后的结果不满足左倾树的条件，则可以通过交换该左倾树的左右子树，使之成为一棵左倾树。

假设一棵左倾树含有n个节点，由于“左倾”的性质，从该树根结点出发，一路沿着右子树向前走，最多走log2(n+1)步(等于树的高度)。又因为左倾树的合并过程总是从右子树方向进行的，这样至多只需要O(log2n)步就可以访问该树右边的子树，同时完成合并工作，这是最坏的情况。显然，左倾树树型最坏的情况是当它的左右子树较为平衡时；最佳树型是当它的所有节点的右指针为空时。

3 结果与分析

试验目的是为了证明改进算法在某市电子地图不同图层上寻径的有效性，并分析搜索半径r和两点间直线距离k对有效性的影响。仿真试验在处理器为Intel酷睿i5 4570(3.2 GHz)、内存4 GB、硬盘1 TB、操作系统为Microsoft Windows 7的微机环境下进行。

3.1 寻径时间

该市电子地图有多个不同的图层，分别含有508，1 033，2 013，3 998条边。选定固定的两个地理位置作为起点和终点，两点间直线距离为k=10 km，同时，搜索半径r设定为2 km，以寻径时间作为衡量算法效率的指标参数，分别从地理距离和拥堵时间两方面来设定边的权值，以对Dijkstra算法、RRSA算法和RSAHSPA算法的效率进行测试，其中RRSA指矩形限制搜索区域算法[12]。

图2描述了在地理距离最短权值下3种算法的寻径时间，在开始边数为508的条件下，Dijkstra、RRSA和RSAHSPA所花费的寻径时间分别为2 110，1 143，632 ms。随着边数的逐渐增加，3种算法花费的寻径时间都逐渐增加，但Dijkstra比RRSA和RSAHSPA增加得更快，同时，RRSA和RSAHSPA所花费的寻径时间增加变化缓慢，并且RSAHSPA算法一直低于RRSA算法。当图层边数增加为3 998条时，3种算法的寻径时间分别为34 412，6 617，3 216 ms。图3描述了在拥堵时间最短权值下3种算法的寻径时间，因此，本文所提方法优于其他两种方法。

图2 寻路访问时间对比(按地理距离最短)Fig.2 Comparison of path finding access time(by geographical distance shortest)

图3 寻路访问时间对比(按拥堵时间最短)Fig.3 Comparison of path finding access time(by congestion time shortest)

3.2 初始半径r的选择

保持上述试验运行环境不变，针对RSAHSPA算法修改k数值，以地理距离最短作为路径权重的情况为例，测试搜索半径r值对算法所花费寻径时间的影响。取k=10 km，初始半径r分别选择r=1,1.5,2,2.5,3 km，运行结果图4所示。

图4 不同初始r值对算法访问时间的影响(k=10 km)Fig.4 Influence of different initial r values on accesstime of algorithm (k=10 km)

另外，取k=5 km，初始半径r分别选择r=0.5,0.7，1,1.5,2 km，运行结果图5所示。

图5 不同初始r值对算法访问时间的影响(k=5 km)Fig.5 Influence of different initial r values on accesstime of algorithm (k=5 km)

为了对照，再取k=20 km，初始半径r分别选择r=1,2,4,6,8 km，运行结果图6所示。

图6 不同初始r值对算法访问时间的影响(k=20 km)Fig.6 Influence of different initial r values on accesstime of algorithm (k=20 km)

试验结果表明，在不同数值k的条件下，随着图层中边数的增加，相同r值下，RSAHSPA算法的寻径时间都会逐渐增大；在同一个数值k的条件下，不同的初始r值对RSAHSPA算法的寻径时间影响显著。例如，在图4的k=10 km条件下，初始r=2, 2.5, 3 km的运行曲线几乎在一起，说明在设置r=2 km 的搜索区域内，已经能够找到一条起点到终点的最短路径，此时，增加r值，对寻径时间影响不大；r=1, 1.5 km需要更多的运行时间，说明在这样的搜索范围内没有找到最短路径，需要增加r值在一个更大的范围内进行搜索，因此时间花费更多。图5和图6中，当r分别增加至1 km和4 km后，再增大搜索半径，对寻径时间影响不大。根据图4～图6结果分析，r=k/5时算法运行效果最好，继续增加r值，效率提高不明显。

4 结论

本文将启发式方法应用到经典的最短路径算法之中，给出了网络地图中的一个新的路径搜索算法。同时，在启发式函数搜索范围和排序方法方面，讨论了算法的改进之处，并将其应用到实现的算法中。仿真试验结果证明了新的路径搜索算法的优越之处，与已有路径选择改进算法相比，能够有效缩短路径查找时间，从而更好地满足出行需要。

[1] DIJKSTRA E W. A Note on Two Problems in Connexion with Graphs[J]. Numerische Mathematics, 1959, 1(1): 269-271.

[2] 汤彬. 一个用左倾树实现O(nlog2n)排序的算法[J]. 微型电脑应用, 1996 (1): 79-83. TANG Bin. A Sorting Algorithm Taking O(nlog2n) Time Using Leftist Tree[J]. Microcomputer Applications, 1996 (1): 79-83.

[3] WEISS M A, 陈越. 数据结构与算法分析: C语言描述 [M]. 2版. 北京:人民邮电出版社, 2005. WEISS M A, CHEN Yue. Data Structures and Algorithm Analysis in C Language[M]. 2nd ed. Beijing: Posts & Telecom Press, 2005.

[4] 章永龙. Dijkstra最短路径算法优化[J]. 南昌工程学院学报, 2006, 25(3): 31-32. ZHANG Yong-long. Optimization of Dijkstra Algorithm [J]. Journal of Nanchang Institute of Technology, 2006, 25(3): 31-32.

[5] 张本群. 基于启发式算法的路径规划[J]. 计算机仿真, 2012, 29(10): 341-343. ZHANG Ben-qun. Path Planning Based on Heuristic Algorithm [J]. Computer Simulation, 2012, 29(10): 341-343.

[6] AGRAWAL R, JAGADISH H V. Materialization and Incremental Update of Path Information[C]∥Proceedings of the 5th International Conference on Data Engineering. Los Angeles:IEEE, 1989: 374.

[7] 严蔚敏, 吴伟民. 数据结构(C语言版) [M]. 北京:清华大学出版社, 1997. YAN Wei-min, WU Wei-min. Data Structure (in C Language) [M]. Beijing: Tsinghua University Press, 1997.[8] 马少平. 人工智能[M]. 北京:清华大学出版社, 2004: 32-34. MA Shao-ping. Artificial Intelligence[M]. Beijing: Tsinghua University Press, 2004: 32-34.

[9] 尼尔松 N J. 人工智能[M]. 北京:机械工业出版社, 1999:145-150. NILSSON N J. Artificial Intelligence: A New Synthesis [M]. Beijing: China Machine Press, 1999:145-150.

[10]张锦明, 洪刚, 文锐, 等. Dijkstra最短路径算法优化策略[J]. 测绘科学, 2009, 34(5): 105-106. ZHANG Jin-ming, HONG Gang, WEN Rui, et al. Optimization Strategies of the Dijkstra’s Shortest Route Algorithm [J]. Science of Surveying and Mapping, 2009, 34(5): 105-106.

[11]邓方安, 雍龙泉, 周涛, 等. 基于“矩阵乘法”的网络最短路径算法[J]. 电子学报, 2009, 37(7): 951-956. DENG Fang-an,YONG Long-quan, ZHOU Tao, et al. Shortest Path Problem Algorithm in Network Based on Matrix Multiplication [J]. Acta Electronica Sinica, 2009, 37(7): 951-956.

[12]王海梅, 周献中. 一种限制搜索区域的最短路径改进算法[J]. 南京理工大学学报: 自然科学版, 2009, 33(5): 638-642. WANG Hai-mei, ZHOU Xian-zhong. Improved Shortest Path Algorithm for Restricted Searching Area[J]. Journal of Nanjing University of Science and Technology: Natural Science Edition, 2009, 33(5): 638-642.

An Improved Path Selecting Algorithm for Traffic Network

DUAN Ming-yi, ZHANG Wen

(School of Information Engineering, Zhongzhou University, Zhengzhou Henan 450044, China)

By using heuristic search method in artificial intelligence, focusing on transport network, on the basis of in-depth analysis of the classical Dijkstra shortest path algorithm, a shortest path algorithm based on heuristic and proved the effectiveness of this method is proposed. After a careful analysis of the improved algorithm, the respects needed to be improved are discussed. Combining with specific applications, the corresponding improvement strategies are proposed from the aspect of heuristic function, searching range and sorting method, and these improvements are applied to the simulation experiment. The result shows that (1)the proposed algorithm has good scalability in different layers; (2) compared with the existing improved path selecting algorithm, the proposed one can effectively shorten the path finding time under different path weight options, thereby to better meet the travel needs. The reference values of the initial search radius for different geographical distance are also given.

ITS; restricted searching area; heuristics; traffic network; path searching; leftist tree

2016-02-16

河南省科技攻关计划项目(162102210327)

段明义(1978-)，男，河南郑州人，硕士，副教授.(duanmingyi@126.com)

10.3969/j.issn.1002-0268.2016.11.018

U491, TP311

A

1002-0268(2016)11-0120-06