黄泛区粉土路基次生盐渍化临界高度研究
姚占勇,滕显飞,毕玉峰,赵 庆,于君彦
(1.山东大学 土建与水利学院,山东 济南 250061;2.齐鲁交通发展集团,山东 济南 250000)
黄泛区粉土路基次生盐渍化临界高度研究
姚占勇1,滕显飞1,毕玉峰2,赵 庆1,于君彦1
(1.山东大学 土建与水利学院,山东 济南 250061;2.齐鲁交通发展集团,山东 济南 250000)
为了分析粉土路基次生盐渍化的临界高度,在室内试验和COMSOL Multiphysics多场耦合数值分析的基础上,研究了黄泛盐渍土区非盐渍粉土路基次生盐渍化盐分迁移规律。研究结果表明,若路基顶部尚未形成聚盐,则路基内部不会形成明显的聚盐夹层,路基内盐分分布从底部向上整体呈现逐渐递减的趋势;建立了黄泛盐渍土区非盐渍粉土路基内部弱盐渍土形成的临界高度与地下水矿化度、地下水位至路基顶部距离的回归公式,估算粉土路基次生盐渍化内部弱盐渍土形成的临界高度;地下水矿化度对粉土路基次生盐渍化的影响程度较地下水埋深或路基填高更为显著。
道路工程;次生盐渍化;数值模拟;临界聚盐高度;回归分析
0 引言
在黄河冲积平原区,地下水埋深较浅且矿化程度较高,气候干燥,蒸发量大,毛细作用剧烈,土壤盐渍化现象十分严重。为了防止路基内盐分聚集而造成次生盐渍化病害,《公路路基设计规范》(JTG D30—2015)[1]规定,盐渍土地区地下水埋深较浅、毛细水上升较高或易受地表水影响的路段,采取抬高路基、设置隔断层、地基换填、路基换填砂砾等技术措施,以抑制或隔断毛细水上升。研究黄泛盐渍土区路基内盐分迁移规律,对于优化路基处置措施,防止黄泛盐渍土区路基次生盐渍化并引发路基病害,具有重要的理论指导意义。
国内外的研究者针对盐渍土区土壤水盐运移规律展开了大量研究。柴寿喜、杨宝珠等[2]研究了渤海湾滨海盐渍土区的盐渍化特征及规律。李新举、张志国等[3]研究表明地面覆盖量可明显控制盐分的表面聚集。通过研究温度梯度对于土壤水盐运移规律的影响,得出温度与土壤水势呈正相关。宋长春[4]针对吉林西部地区地下水特征,探讨了潜水埋深、矿化度、组成、径流条件等对内陆盐渍化土壤形成的影响。张堃[5]研究了黄泛区地下水埋深、地下水矿化度等对路基水分和盐分运移的影响。朱登元、管延华[6]研究了毛细水对粉土路基稳定性的影响。刘广明等[7]建立了地下水累积蒸发量与地下水埋深、地下水矿化度的关系。以上研究均未涉及盐渍土区非盐渍粉土路基次生盐渍化规律系统的定性分析。
本文在室内试验和COMSOL Multiphysics多场耦合数值分析的基础上,研究了黄泛盐渍土区路基内部盐分的迁移聚集规律,并得出了路基内部临界聚盐高度和地下水矿化度、地下水埋深、路基填高等之间的回归关系式,对黄泛盐渍土区的公路建设具有重要的理论价值。
1 竖管法试验研究
1.1 竖管法试验原理及方法
张堃[5]指出,路基模型与竖管模型在毛细水上升高度随时间的变化规律、含水率及含盐量随高度的变化规律上基本一致,因此可以使用竖管来近似替代路基模型对路基内水分和盐分的运移规律进行研究。基于此,本文利用竖管法来近似代替路基模型模拟黄泛区粉土路基的盐分迁移聚集规律,同时与竖管数值模拟结果进行对比,二者相互验证。
竖管内的土体采用分层填筑的方法,竖管填筑过程中土的平均含水率保持最佳含水率15.4%,与道路分层铺筑的高度相同,每层压实后层高25 cm,竖管内土柱的高度为3.9 m,竖管填装完毕后,竖管底面放置在含盐量为30 g/L的盐水中,检测90 d后竖管内各检测点点位的含水率和含盐量。为了保证试验数据的准确性,竖管模型做两组平行试验,分别记为S1、S2。
1.2 试验用土的基本性质
根据《公路土工试验规程》(JTG E40—2007)[8]可得试验用土的基本性质,如表1、表2所示。

表1 土的颗粒组成Tab.1 Composition of soil particle

表2 土的物性指标Tab.2 Physical property indexes of soil
从表1、2可以看出,黄泛区粉土粒径小于0.075的粉黏粒含量占66.5%,各粒径含量所占比例不均匀。该类土具备发达的毛细通道,毛细作用强烈。
1.3 试验结果及分析
竖管内含水率、含盐率随高度的变化如图1、图2所示。由图1可以看出,随着高度的增加,竖管土体的含水率逐渐减小。在竖管模型的最下部,粉土的含水率在29%左右,达到粉土的液限值,接近饱和状态。在竖管模型的顶部,土的含水率在10%左右,土的含水率与填筑时含水率有明显的下降,说明竖管顶部已经离开毛细水的影响范围,在蒸发作用影响下,顶部含水率有所下降,根据《公路土工试验规程》(JTG E40—2007)[8]毛细管水上升高度试验,可得所用粉土毛细水最大上升高度约为2.35 m。

图1 含水率随高度的变化图Fig.1 Water content varying with height

图2 含盐量随高度的变化图Fig.2 Salt content varying with height
由图2中可以看出,水中的盐分在毛细水的带动下向上迁移,随着高度的增加,土中的含盐量呈现先减小后趋于稳定的规律,由下至上盐分的含量逐渐减少,且竖管内部没有形成聚盐层。在地下水含盐量为30 g/L的条件下,高度100 cm以上的部分,土的含盐量均在0.3%以下,最后稳定在0.2%左右。由图2可知,在竖管80 cm以上的区域并未形成盐渍土。竖管试验结果说明当地下水矿化度为30 g/L时,弱盐渍土90 d形成的临界高度为地下水位以上80 cm左右,内部也未形成聚盐层。
对比图1与图2,由竖管底部向上含水率和含盐量逐渐降低,到1~1.2 m高度处后含水率与含盐率均开始趋于稳定,说明在竖管土中的含水率和含盐量的递减规律具有一致性,毛细水的上升运动对于盐分迁移有着明显影响。
2 弱盐渍土形成临界高度的数值分析
粉土路基在盐渍土地基区发生次生盐渍化的过程可以分为两个物理场:水分在非饱和土体的路基中在毛细作用(基质吸力)影响下的运动、盐分作为溶质随水分运动而运动的溶质运移。为了更准确地揭示黄泛盐渍土区非盐渍粉土路基内部的盐分迁移聚集规律,本文拟采用COMSOL Multiphysics进行两个物理场(基于理查德方程和溶质运移方程)的耦合,对粉土路基在盐渍土地基区发生次生盐渍化的规律做进一步的研究,同时将室内竖管试验结果与竖管数值模拟90 d的结果进行对比,验证COMSOL Multiphysics数值模拟的合理性。
2.1 竖管法数值模拟
2.1.1 计算模型
建模构造竖管模型见图3,模型采用较细化网格划分。其中,1和4边界为无流通边界,2边界为含盐地下水流入边界,3边界为流出蒸发边界。

图3 竖管模型图(单位:m)Fig.3 Standpipe model(unit:m)
2.1.2 计算结果
图4为模拟的竖管盐分浓度分布图,从图中可以看出竖管底部盐浓度为30 kg/m3,随着毛细水的上升和上边界的持续蒸发作用,盐分进一步向上扩散。土的最大干密度为1 785 kg/m3,根据《公路路基设计规范》(JTG D30—2015)[1]取含盐量0.3%为盐渍土和非盐渍土的分界点,则对于模型内部临界值为盐分含量5.355 kg/m3,以此值作为分界线在图4中标记出。在数值模拟中,弱盐渍土形成的临界高度于105 cm处,盐分自下而上浓度逐渐降低且内部没有形成聚盐层。

图4 盐分浓度分布图(单位:kg/m3)Fig.4 Salt concentration distribution (unit:kg/m3)
2.1.3 与室内竖管试验对比
为了方便对比,统一将含盐量试验值与计算值转化为百分比,如图5所示。
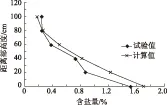
图5 试验值与计算值对比Fig.5 Comparison of experimental and calculated values
从图5中可以看出,竖管1 m以下测点模型内的含盐量与数值模拟所得含盐量基本吻合,对于1~3.9 m段模型实测含盐量稳定在0.2%,数值计算含盐量向上逐渐递减为0,竖管顶部未形成聚盐。使用数值模拟来模拟竖管内盐分迁移变化规律与试验得出的变化规律是基本一致的。随着毛细水的上升盐分由下部向上部迁移,随着高度的增加,土中的含盐量在逐渐减小,土体内部无明显盐分聚集带。路基聚盐层形成的两个必要条件:含盐地下水、毛细水上升高度高于路基。当毛细水上升高度高于路基时,在蒸发作用下,盐分在路基顶部不断析出,最终形成聚盐层;当毛细水上升高度低于路基顶部时,在毛细水的作用下,盐分不会析出,最终形成一种自下而上的浓度梯度。
图5中试验值和计算值之间的些微差别,主要原因有:(1)含盐量测量试验中由于仪器精度限制;(2)在数值计算过程中,偏于安全的将边界蒸发条件的设置为恒定值区域最大蒸发强度10 mm/d[9-10],与实际情况不同产生的误差,尤其是蒸发边界条件在实际情况中比较复杂,很难准确在模型中进行动态定义;(3)竖管试验中水中的含盐量并不是一个恒定值,水中含盐量的波动对盐分的迁移也会产生一定的影响。在误差允许的范围内可通过数值模拟来研究黄泛盐渍土区非盐渍粉土路基次生盐渍化的盐分迁移规律。
2.2 路基模型模拟
在竖管试验的基础上验证了COMSOL Multiphysics多场耦合数值分析的合理性,并对次生盐渍化临界聚盐高度进行了初步探讨,通过建立路基模型借助数值模拟对黄泛盐渍土区路基次生盐渍化的临界聚盐高度做进一步的探究。
2.2.1 基本假定
(1)地基土体与路基土体是均质同性的;
(2)路基填筑过程中盐分的迁移作用忽略不计;
(3)蒸发强度、温度、地下水埋深等外界条件维持稳定;
(4)降雨条件对路基内部盐分的影响忽略不计。
2.2.2 计算参数
根据室内试验所得试验用土基本性质、COMSOL使用手册及VG模型参数[11-15],可得数值模拟时所需参数如下:
饱和渗透系数Ks=0.02 cm·h-1=4.8×10-3m/d;饱和含水量θs=0.36;残余含水量θr=0.07;模型参数a=0.005 cm-1= 0.5 m-1;模型参数n=1.09;模型参数m=0.083;最佳含水率ω=0.154,体积含水量θ=0.235;盐分纵向扩散系数0.005,盐分横向扩散系数0.001;盐分液相扩散系数Dl=3.74×10-2m2/d;依托试验路实测数据,蒸发强度保持区域最大蒸发强度10 mm2/d;模拟时长365 d。
2.2.3 影响因素的取值:
对于黄泛盐渍土区,影响地下水盐分上升的因素较为复杂,主要有路基高度、地下水埋深、地下水矿化度、蒸发强度等,蒸发强度的年际变化较不规则,因此此处拟用路基高度、地下水埋深、地下水矿化度作为参变数,研究其对弱盐渍土形成高度的影响。
为方便计算,基于基本假定,此处做进一步的简化处理,将影响因素中的路基高度和地下水深度合并为地下水位到路基顶部的距离,此时主要影响因素为:
总高度H:2~11 m
地下水矿化度:10~38 g/L。
2.3 计算结果及分析
2.3.1 数值模拟计算结果如表3所示。

表3 弱盐渍土临界高度计算表Tab.3 Calculation table of critical height of weak saline soil
注:临界高度以地下水位为零参考面。
假设回归估算表达式为:
h=b0+b1H+b2C+b3HC+b4H2+b5C2,
试对其回归系数进行估算并进行回归分析,分析结果如表4~表6所示。

表4 回归统计Tab.4 Regression statistics

表5 方差分析Tab.5 Analysis of variance

表6 回归参数Tab.6 Regression parameters
从表4中可以看出,MultipleR(复合相关系数)为0.994 6,表明弱盐渍土内部临界高度与地下水矿化度和地下水位到路基顶部的总距离高度相关,标准误差为0.047 5,说明拟合程度非常高。表5中的SignificanceF(F显著性统计量)的P值为7.46×10-22,远远小于显著性水平0.05,表明该回归方程效果非常显著。据此,由表6可以得出估算的回归方程为:
h=0.436 1-0.096 3H+0.119 8C+0.000 2HC+
0.006 2H2-0.001 52C2。
(1)
2.3.2 方程分析
进一步分析回归方程(1)可得到:回归方程(1)中的一次项H的系数为负,表明单独增加路基高度或降低地下水位能够降低弱盐渍土形成的内部临界高度;一次项C的系数为正,表明地下水矿化度的增大会提高弱盐渍土形成的内部临界高度;交互项的系数为0.000 2(t=-0.420 1,P>0.25,不显著),表示总高度和地下水矿化度的交互作用是微弱的正效应;二次项H2的系数为正,表明路基顶部到离地下水位距离达到一定的高度后,随着距离的进一步增加对弱盐渍土形成的内部临界高度具有微弱的促进作用,对于黄泛区路基来说其二次项作用可忽略不计;二次项C2的系数为负,表明过大的地下水矿化度会抑制弱盐渍土形成的内部临界高度,因为地下水中所含的盐分及浓度影响着毛细水强烈上升高度,一般来说随着地下水矿化度的增加,毛细水强烈上升高度有所降低,而土中盐分的迁移聚集是以毛细水作为载体,因此当地下水矿化度过大时会对盐分的向上迁移产生一定的抑制作用。这与客观现象相符合,对工程实践具有一定的参考价值。
在回归方程(1)中不能直接通过对比系数的大小来判断两个影响因素与弱盐渍土内部临界高度的密切程度。此处可以直接通过回归系数的显著性来判断两者(自变量)与弱盐渍土内部临界高度(因变量)的密切程度,而不需要通过复杂的偏相关或通径分析来判断。因为回归和相关系数存在内在的联系,相关系数是标准化(去单位)的回归系数,两者检验的可靠性必然一致[16]。回归系数b1的显著性P=0.000 62,b2的显著性P=2.16×10-12,两者t统计量的P值均小于显著性水平0.05,因此该两项的自变量与因变量相关,二者对比,b2的显著性更高,表明总高度H和地下水矿化度C两者相比,地下水矿化度C对弱盐渍土形成的内部临界高度的影响大于总高度H对内部临界高度的影响。由公式可知,当总高度小于20 m时,弱盐渍土形成的内部临界高度小于2.85 m。路基边坡弱盐渍土形成的临界高度根据表6计算结果可在路基内部弱盐渍土形成的临界高度的基础上增加一个安全值,即h′=h+0.8。
3 结论
(1)路基聚盐层形成的两个必要条件为含盐地下水、毛细水上升高度高于路基。当毛细水上升高度高于路基时,在蒸发作用下,盐分在路基顶部不断析出,最终形成聚盐层;当毛细水上升高度低于路基顶部时,在毛细水的浸润作用下,路基内部不会形成明显聚盐夹层,整体呈一种自下而上的浓度梯度递减趋势。
(2)黄泛盐渍土区非盐渍粉土路基内部弱盐渍土形成的临界高度与地下水矿化度、地下水位至路基顶部距离可建立相关计算公式,可估算粉土路基次生盐渍化内部弱盐渍土形成的临界高度。
(3)黄泛盐渍土区粉土路基次生盐渍化程度受地下水矿化度影响最为显著,其次为地下水位至路基顶部的距离。
[1] JTG D30—2015,公路路基设计规范[S]. JTG D30—2015,Specifications for Design of Highway Subgrade[S].
[2] 柴寿喜,杨宝珠,王晓燕,等. 渤海湾西岸滨海盐渍土的盐渍化特征分析[J]. 岩土力学,2008,29(5):1217-1221,1226. CHAI Shou-xi,YANG Bao-zhu,WANG Xiao-yan,et al. Analysis of Salinization of Saline Soil in West Coast Area of Bohai Gulf [J]. Rock and Soil Mechanics,2008,29 (5):1217-1221,1226.
[3] 李新举,张志国. 秸秆覆盖对土壤水分蒸发及土壤盐分的影响[J]. 土壤通报,1999,30(6):257-258. LI Xin-ju,ZHANG Zhi-guo. Effect of Straw Mulching on Soil Water Evaporation and Soil Salinity [J]. Chinese Journal of Soil Science,1999,30 (6):257-258.
[4] 宋长春,邓伟. 吉林西部地下水特征及其与土壤盐渍化的关系[J]. 地理科学,2000,20(3):246-250. SONG Chang-chun,DENG Wei. Characteristics of Groundwater in West of Jilin and Its Relationship with Soil Salinization [J]. Scientia Geographica Sinica,2000,20(3):246-250.
[5] 张堃. 黄泛盐渍土地区路基水盐迁移及隔断技术研究[D].济南:山东大学,2012. ZHANG Kun. Yellow River Saline Soil Subgrade Water and Salt Migration and Partition [D]. Jinan:Shandong University,2012.
[6] 朱登元,管延华. 毛细水作用对粉土路基稳定性的影响[J]. 山东大学学报:工学版,2012,42(1):93-98. ZHU Deng-yuan,GUAN Yan-hua. The Influence of Capillary Water Action on the Embankment Stability of a Silt Embankment[J]. Journal of Shandong University :Engineering Science Edition,2012,42 (1):93-98.
[7] 刘广明,杨劲松,李冬顺.地下水蒸发规律及其与土壤盐分的关系[J].土壤学报,2002,39(3):384-389. LIU Guang-ming,YANG Jin-song,LI Dong-shun. Evaporation Regularity and Its Relationship with Soil Salt [J]. Acta Pedologica Sinica,2002,39 (3):384-389. [8] JTG E40—2007,公路土工试验规程[S]. JTG E40—2007,Test Methods of Soils for Highway Engineering [S].
[9] 洪嘉琏,傅国斌,郭早男,等.山东南四湖水面蒸发
实验研究[J].地理研究,1996,15 (3):42-49. HONG Jia-lian,FU Guo-bin,GUO Zao-nan,et al. Experimental Research on the Water-surface Evaporation of Nansi Lake in Shandong Province[J]. Geographical Research,1996,15 (3):42-49.
[10]王积强. ГГИ-500-50型土壤蒸发器在山东德州地区的应用[J]. 水文,1982(4):47-49. WANG Ji-qiang. Application of ГГИ-500-50 Type Soil Evaporator in Dezhou,Shandong[J]. Hydrology,1982(4):47-49.
[11]张华,周小超. 一种基于VG模型的非饱和土渗流参数反演方法[J]. 三峡大学学报:自然科学版,2012,34(3):64-68. ZHANG Hua,ZHOU Xiao-chao. A Back Analysis Method for VG Model Parameters in Unsaturated Seepage Simulation[J]. Journal of China Three Gorges University:Natural Science Edition,2012,34 (3):64-68. [12]王志涛,缴锡云,韩红亮,等.土壤垂直一维入渗对VG模型参数的敏感性分析[J].河海大学学报:自然科学版,2013,41(1):80-84. WANG Zhi-tao,JIAO Xi-yun,HAN Hong-liang,et al. Sensitivity Analysis of VG Model Parameters with Vertical One-dimensional Soil Infiltration[J]. Journal of Hohai University:Natural Science Edition,2013,41 (1):80-84. [13]范严伟,邓燕,王波雷.土壤水分特征曲线VG模型参数求解对比研究[J].人民黄河,2008,34(5):49-50. FAN Yan-wei,DENG Yan,WANG Bo-lei. Comparative Study on Solution of Soil Water Characteristic Curve VG Model Parameters [J]. Yellow River,2008,34(5):49-50.
[14]彭建平,邵爱军. 基于Matlab方法确定VG模型参数[J].水文地质工程地质,2006(6):25-28. PENG Jian-ping,SHAO Ai-jun. Determination of the Parameters of VG Model Based on Matlab [J]. Hydrogeology & Engineering Geology,2006 (6):25-28. [15]彭建平,邵爱军. 用MatLab确定土壤水分特征曲线参数[J]. 土壤,2007,39(3):433-438. PENG Jian-ping,SHAO Ai-jun. Determination of Parameters of Soil Water Characteristic Carve by MatLab [J]. Soils,2007,39(3):433-438.
[16]田生昌. Excel软件在非线性回归分析中的应用探讨[J]. 宁夏农林科技,2011,52(11):29-31. TIAN Sheng-chang. Excel Software Used for Multi-nonlinear Regress Analysis and Discussion [J]. Ningxia Journal of Agriculture and Forestry Science and Technology,2011,52(11):29-31.
Study on Critical Height of Secondary Salinization of Silty Soil Subgrade in Yellow River Impact Plain Area
YAO Zhan-yong1,TENG Xian-fei1,BI Yu-feng2,ZHAO Qing1,YU Jun-yan1
(1. School of Civil Engineering,Shandong University,Jinan Shandong 250061,China;2. Qilu Transportation Development Group,Jinan Shandong 250000,China)
In order to study the critical height of secondary salinization of silty soil subgrade, the migration law of salt in the secondary salinization of non-saline soil subgrade in the Yellow River impact plain area is studied based on the laboratory test and the numerical analysis of COMSOL multiphysics multi-field coupling. The result shows that (1) if the top of subgrade has not yet formed poly salt, the roadbed internal cannot obvious form salt accumulation layer, and the salt distribution in the subgrade shows the trend of gradually decreasing from the bottom to the top; (2) the regression formula of critical height with groundwater mineralization degree and the height of the underground water level to the top of subgrade of the internal weak saline soil of non-saline soil subgrade in the Yellow River impact plain area is established, which could be used for estimation of the critical height of internal weak saline soil of secondary salinization of silty soil subgrade; (3) the influence of the groundwater mineralization degree is significantly higher than that of the buried depth of groundwater and the filling height of subgrade on the secondary salinization of silty soil subgrade in the Yellow River impact plain area.
road engineering; secondary salinization; numerical simulation; critical salinity accumulation height; regression analysis
2016-02-24
姚占勇(1966-),男,山东济南人,教授,博士生导师.(zhanyong-y@sdu.edu.cn)
10.3969/j.issn.1002-0268.2016.11.009
U419.5
A
1002-0268(2016)11-0057-06

