基于价差分析建立国债期货跨期套利模型

徐倩倩，许纪校，杨军峰

(河海大学 商学院，南京211100)



基于价差分析建立国债期货跨期套利模型

徐倩倩，许纪校，杨军峰

(河海大学 商学院，南京211100)

国债期货交易初期以期现套利和跨期套利等投资方式为主.跨期套利以预测跨期价差为基础，此前有关股指期货及国债期货跨期套利的研究往往忽略了对跨期价差的分析.根据已有相关文献，总结得出均值方差模型、协整GARCH模型两个常用的跨期价差预测模型，并且认为自回归模型也在一定程度上适用于价差预测.分别用这三个模型对实际价差进行预测，通过检验预测结果得出以自回归模型为基础的最优价差预测模型.

国债期货；跨期价差；跨期套利；自回归模型

早在1978年，William Poole等人就开始研究期货价格的决定因素[1-2].当今投资市场及学术界广为采用的持有成本理论，主要来源于Cornell和French在1983年研究得出的持有成本模型[3].该模型在股指期货相关套利方面适用性较高，但由于国债期货特殊性加上模型本身设定存在一定问题，其在国债期货套利应用中遇到了较大困难.Chow等研究1982年美国期货市场、Hegde和Branch研究国芝加哥商品交易所国债期货价格均发现存在模型所包含的交易成本之外的市场成本[4-5].Capozza等根据无套利原理进行模拟测算得出国债期现市场最终均衡状态；但该研究基于国债期现价格随机变动的假设[6].持有成本理论可得出股指期货理论价格，再利用无套利原则考虑交易成本得到股指期货无套利区间[7-9].根据这种方法Yadav和Pope对跨期价差进行了直接研究，发现价差序列存在显著的均值回复现象[10].经证明，该现象广泛存在于金融数列中，基于此本文将对国债期货跨期价差序列进行长记忆检验和方差比检验，判断序列是否存在均值回复现象.

近年来较多学者将注意力集中到了统计套利方面.康瑞强研究了上海期货交易所2009年沪铜Cu11和沪铜Cu12期货合约数据两者之间跨期价差，建立了协整模型，并以此建立了统计套利模型[11].Carol在研究指数统计套利时就用到了协整方法[12].除了协整模型，近年来较多地用于统计套利的方法还有均值回归法，也就是基于均值回复现象的均值方差模型.在我国金融期货跨期套利研究中，有一种常用于预测的自回归模型却鲜有人用于期货套利.近年来，陈彦晖研究结果显示基于自回归移动平均模型(ARMA)模型的套利实现了较好的收益；另外他还在模型中引入GARCH模型，最终分析认为GARCH模型的引入改善了预测结果[13].一般认为像国债期货跨期价差这种金融数据，特别是分时金融数据自相关程度较高，因此有理由认为国债期货跨期价差的预测可运用自回归模型.

1 国债期货跨期价差研究模型

可以说对跨期价差的研究与把握是进行跨期投资的充分条件.国债价格或是国债期货价格影响因素众多，如果不进行全面分析，最终结果不可靠[14-15].如果将投资依据转换成跨期价差，则投资策略的确定将变得简单.因为价差的影响因素更少，跨期价差更加稳定，研究价差的模型众多，理论相对成熟.

将国债期货跨期价差与股指期货作简单比较，可更加清晰地得出前者的一般特征.股指期货跨期价差受到三个因素影响：股指价格、融资利率、股指收益率.而且股指期货跨期价差公式的推出不需要多余的假设，较为符合实际情况，再加上股指期货交易标的确定，不存在转换期权、月末期权等因素，其跨期价差更加明确.于是可发现国债期货跨期价差存在以下几个特征：定价公式不够准确、很难根据定价公式建立无套利区间、套利机会更多.可见国债期货跨期价差在理论上存在更大的不确定性，且不存在一个标准的定价公式，故选用统计套利类方法对跨期价差进行分析.

1.1 均值方差模型

一般情况下，影响国债期货价格变化的因素对两只国债期货存在相同方向的影响，因此跨期价差往往比国债期货价格本身更加稳定.也就是说其趋势或是状态发生巨大变化所需时间更长，因此其存在均值回复现象的可能性很大.于是可用一定期限内跨期价差平均值作为当期价差的估计值，价差序列历史波动率的移动平均作为实际价差波动率的估计建立均值-方差模型.

1)长记忆性(R/S)检验及其结果

长记忆指的是某个扰动是否对序列存在长远的作用，如果序列存在长记忆性，则当偏离均值的趋势产生之后很难消除，均值回复理论也就不再适用.在金融序列的应用当中普通的长记忆检验无法排除异方差、短记忆现象的干扰，为了解决该问题，随之产生了修正长记忆模型.该模型的主要公式如下.

其中:mean(x)、var(x)分别表示x序列均值和方差.修正模型最终得到统计量V(q)，当该统计量落在[0.809,1.862]之间时拒绝序列x存在长记忆性的假设，表明x存在均值回复现象.变量q的选择是模型的重点之一，考虑到q=0时修正长记忆模型退化为普通的长记忆模型，而当q过大时模型会忽略长记忆的影响，本文的研究中取q从1～12时(保守估计)对应V(q)统计量的平均值作为最终统计量.价差序列是取每隔15min的数据.用MATLAB2013b进行计算，结果为V=1.8609，表明价差序列存在均值回复现象.

2)方差比检验及结果

方差比检验的主要公式如下：

最终得到比值VR(k)，k表示在收益序列rt,k中计算收益时的时期跨度，一般选取k≥3，显然当VR值大于1时表明跨期较长时收益波动大于跨期短时的收益波动，原序列x可能存在趋势性波动，不存在均值回复现象；当VR值小于1时表明较长跨期的收益波动小于短跨期波动，序列x存在均值回复过程.在MATLAB2013b环境下对国债期货跨期价差进行方差比检验，当k选取3时，VR值为0.415，随着k的增大VR值减小，表明价差序列存在均值回复过程.由此可判断国债期货跨期价差序列存在均值回复现象，可以利用均值-方差模型对跨期价差进行预测.

1.2 协整GARCH模型

协整理论通过拟合两只国债期货价格，可以得出动态均衡价差.国债期货价格拟合方程中往往存在自相关现象，如果其残差存在ARCH效应，则可引入GARCH模型分离立方差，得到动态价差波动.协整理论挽救了非平稳序列之间的回归拟合.该理论认为如果非平稳序列进行回归，所得回归结果中的残差序列是平稳的，则这些非平稳序列协整，可以认为他们之间存在着长期关系.

1)首先对传统方法得到的协整方程进行异方差检验，检验方法为White检验.确定方程存在异方差性之后即可建立GARCH模型.

2)接着需要确定GARCH(p，q)模型具体形式，即确定p和q的值.由于本文选取的是间隔15 min的交易数据，较长滞后期的回归残差均会对当期残差方差产生较大影响，所有优先考虑GARCH(1,1)模型.拟合之后，再对结果进行残差分析，判断是否还存在ARCH效应，如果不存在，且回归结果符合模型假设，即得到最终模型和结果.否则就修改模型，继续上述步骤.

3)根据最终模型和结果，就可对均衡价差和时变方差进行预测.以GARCH(1,1)模型为例的方差预测公式如组合公式(1)所示：

(1)

由式(1)便可预测任意k期之后的条件方差.其中:α0、α1、β1分别为GARCH模型中的常数项、ARCH项、GARCH项系数.将预测所得的均衡价差和方差与实际价差和价差波动进行对比检验，即可通过比较预测效果判断各模型对于跨期价差的预测精度.

1.3 自回归模型

自回归(AR)模型是一种线性预测，即已知N个数据，可由模型推出第N点前面或后面的数据，所以其本质类似于插值，但AR模型要比插值方法效果更好.

1.3.1 自回归模型的建立

自回归模型的基本公式：yt=α1yt-1+α2yt-2+αiyt-i+…+ut

根据期货定价公式得出的价差公式可知影响国债期货价差的因素主要有国债现券全价和融资利率.这两个因素在短周期内的变动主要由市场因素造成，因此对于短周期数据来说，其更加容易受到前几期价格影响，自回归模型能有效预测均衡价差与价差波动率.为此对价差序列构建自回归模型，并检验其异方差性，如果存在异方差则再建立自回归-GARCH模型.

1.3.2 自回归-GARCH模型

自回归模型是拟合国债期货跨期价差较好的模型之一，但仍存在这样一种可能：存在某些因素，对长期限或者短期限期货的价格影响比较大，而对另外期限的期货价格影响相对较弱，则该因素波动的增加将引起价差波动增加.GARCH模型自回归条件异方差(ARCH)模型的一个推广，它的引入可以解决以上问题.ARCH模型将回归估计分为均值方程和方差方程两个部分，并且认为残差序列方差受到前几期残差平方的影响，其具体方程式如下：

yt=γ0+γ1x1t+…+γkxkt+ut

当方差方程中滞后阶数p较大时，回归模型待估值过多使得模型无法估计，Bollerslev于1986年通过用方差的滞后项代替多个残差平方的滞后项，从而减小了模型的待估参数，ARCH模型由此扩展成为GARCH模型.最简单的GARCH(1,1)模型方程式如下：

yt=xtγ+ut

其中:xt是外生变量向量，ut-1是所谓的ARCH项，及GARCH(1,1)中的第二个1，表示模型中残差平方项滞后到一阶.由此我们便可以利用最大似然估计法对模型参数进行估计，并据此对方差进行预测.

1.4 跨期价差预测模型初步分析

基于均值回复现象的均值方差模型和协整模型是较为常用的统计套利模型，本文在研究文献的基础上认为自回归模型也能够很好的预测跨期价差，特别是对于采用分时数据的国债期货跨期价差.跨期价差预测精度决定了跨期套利效率，有必要对三大模型预测结果进行比较研究.为此本文将选取了国债TF1409和TF1412组合产生跨期价差，生成190个计算样本点和30个验证样本数据.分别用三大模型得到跨期价差以及跨期价差波动水平的预测值.

2 国债期货跨期套利模型研究

2.1 各价差预测模型数据预测结果

2.1.1 均值-方差模型

根据均值回复理论，国债期货跨期价差有较大概率从偏离值回复到平均值，于是将价差序列历史平均值作为其估计值，历史方差作为其波动的估计值，历史方差的计算方法为取相邻两期真实价差的对数差.得到结果如表1所示.

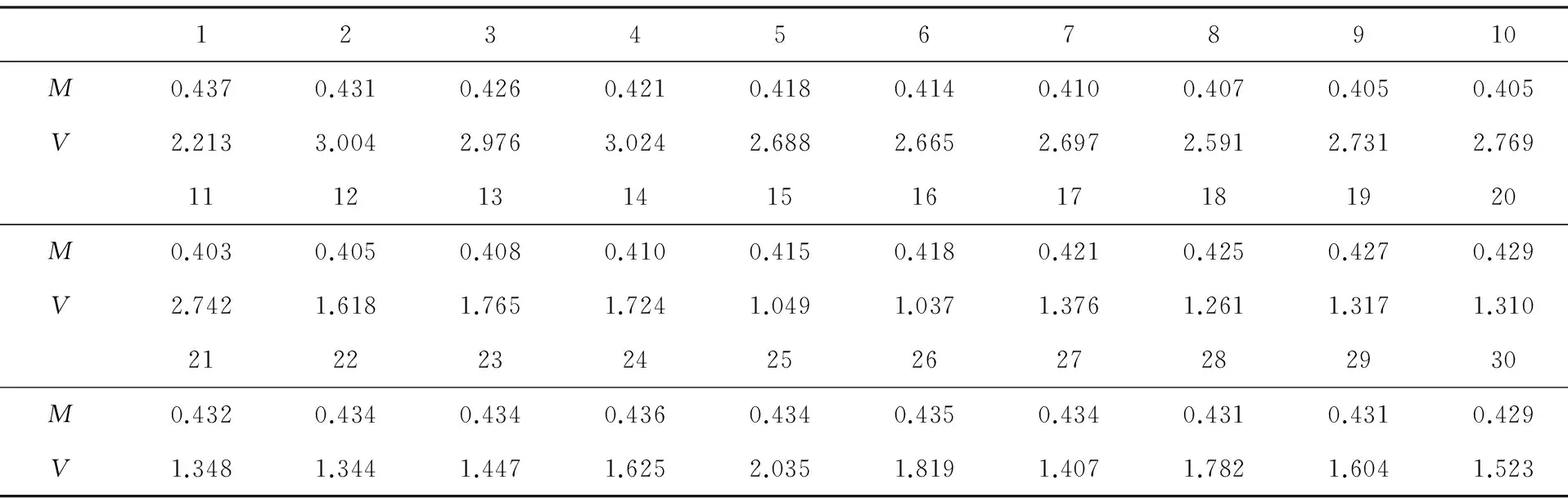
表1 均值-方差模型计算结果

12345678910M0.4370.4310.4260.4210.4180.4140.4100.4070.4050.405V2.2133.0042.9763.0242.6882.6652.6972.5912.7312.76911121314151617181920M0.4030.4050.4080.4100.4150.4180.4210.4250.4270.429V2.7421.6181.7651.7241.0491.0371.3761.2611.3171.31021222324252627282930M0.4320.4340.4340.4360.4340.4350.4340.4310.4310.429V1.3481.3441.4471.6252.0351.8191.4071.7821.6041.523

其中:M、V分别表示计算得出的移动平均值和方差值，方差显示的是乘以10 000后的结果.

2.1.2 协整GARCH模型

单位根检验显示，两个期货价格变量均为一阶单整，于是进行回归，得到结果如表2.

表2 协整模型回归结果

TF1412(应变量)系数T统计值P值TF14090.976226.5790.000常数项2.5776.4060.000ADJ-R20.996DW值0.723

1)协整检验

检验方法为E-G两步法.表2已经完成了E-G两步法中的第一步，只需对该回归的残差序列进行单位根检验即可判断两变量之间是否存在协整关系.对残差进行单位根检验，得到相应t统计值为-3.799.此时对应的临界值表发生了变化，相比于原来的临界值，E-G两步法中的临界值更加苛刻，具体的数值可参考恩格尔和格兰杰提出的临界值表.在两变量模型中，1%和5%水平对应的临界值分别是-3.956和-3.369，显然残差序列在5%的水平下拒绝存在单位根的原假设，认为原方程存在协整关系.

2)协整GARCH模型

经检验原协整模型存在异方差现象，故对模型建立GARCH(1,1)模型，得到结果如表3所示.

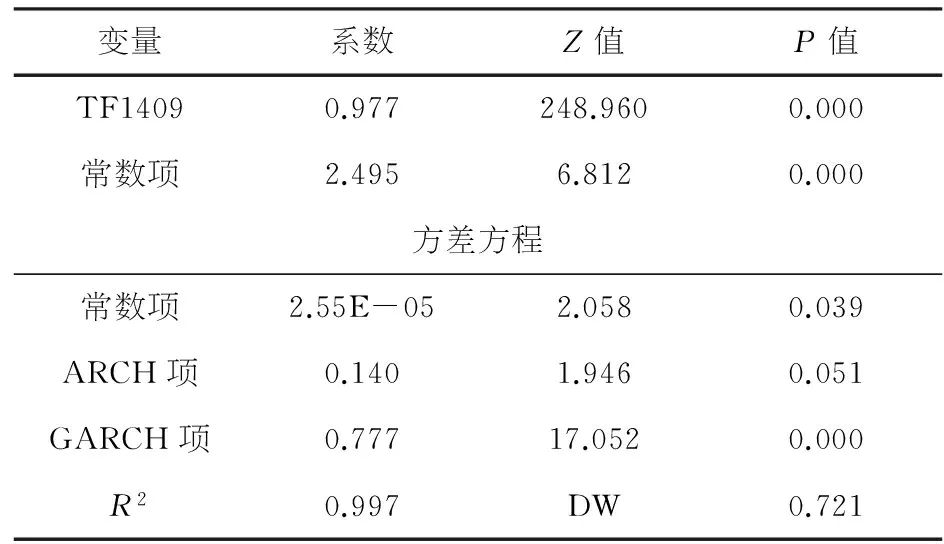
表3 模型GARCH(1,1)模型结果

变量系数Z值P值TF14090.977248.9600.000常数项2.4956.8120.000方差方程常数项2.55E-052.0580.039ARCH项0.1401.9460.051GARCH项0.77717.0520.000R20.997DW0.721

由表3可知，最大似然估计结果与此前协整回归结果较为一致，各变量保留了较高的显著性，可决系数和DW值也较为接近，且方程整体拟合优度很高，R2十分接近1.模型方差方程中所有系数均为正数，符合假设；ARCH项和GARCH项的和为0.917，接近于1，符合常理.经过ARCH检验可知此时模型不再存在异方差，因此表3即为协整-GARCH模型最终结果.

由此得出模型均衡价差计算公式如式(2)所示，

DTF=-0.023*TF1409+3.714

(2)

时变方差如式(3)所示，

(3)

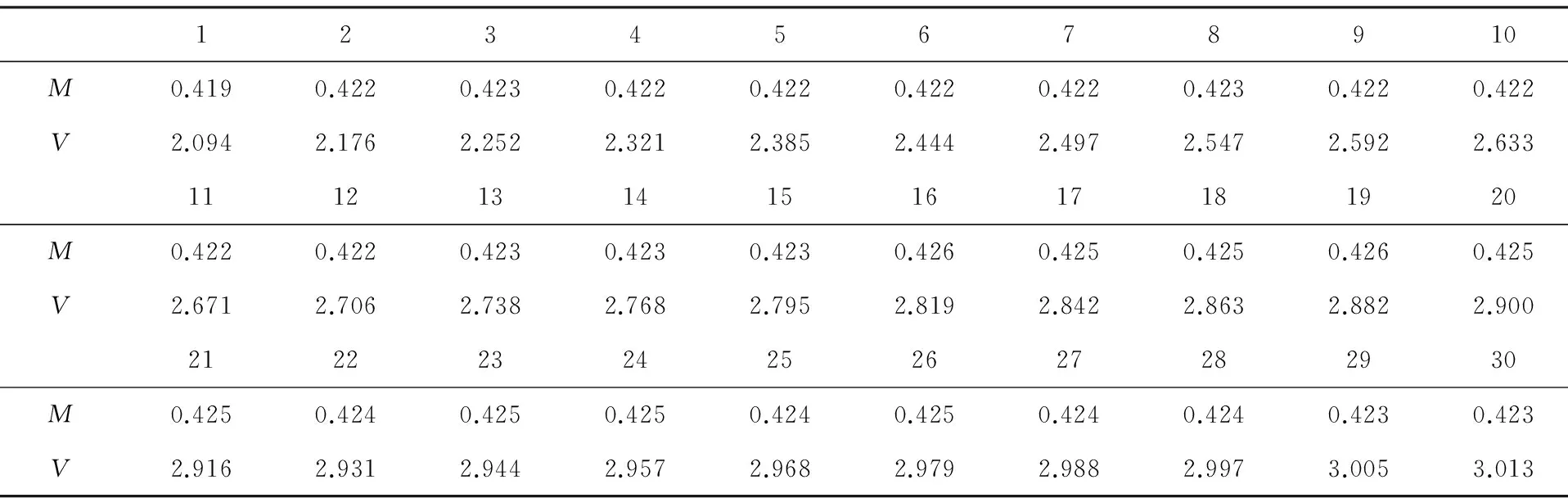
表4 协整GARCH模型均衡价差与时变方差估计值

12345678910M0.4190.4220.4230.4220.4220.4220.4220.4230.4220.422V2.0942.1762.2522.3212.3852.4442.4972.5472.5922.63311121314151617181920M0.4220.4220.4230.4230.4230.4260.4250.4250.4260.425V2.6712.7062.7382.7682.7952.8192.8422.8632.8822.90021222324252627282930M0.4250.4240.4250.4250.4240.4250.4240.4240.4230.423V2.9162.9312.9442.9572.9682.9792.9882.9973.0053.013

2.1.3 自回归模型

首先需确定自回归模型中的滞后阶数，确定方法有两个方向：1)从少至多.先从滞后一阶开始对模型进行估计，然后对残差进行LM相关性检验，如果模型存在自相关，则添加滞后项.过程中考虑可决系数等模型统计量的变化.2)从高至低.首先建立包含多个滞后期的估计模型，剔除变量不显著的滞后项.综合运用上述两种视角，发现模型中包含DTF变量的1-3阶滞后项时模型拟合优度最高，不存在自相关，且所有变量都通过5%水平下的显著性检验.

异方差性是得到时变方差的前提，为此需要对上述模型进行异方差检验.检验方法为ARCH检验和White检验，该检验方法通过构造辅助回归方程，方程的R2和样本量的乘积近似于特定分布，通过判定该乘积的实际值即可判定原假设的可信度.检验结果如表5所示.

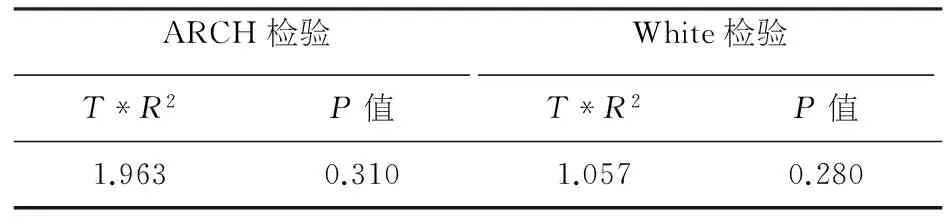
表5 模型异方差检验结果

ARCH检验White检验T*R2P值T*R2P值1.9630.3101.0570.280

White检验中选择存在交叉项，ARCH检验的滞后阶数由检验方程系数的显著性判断，滞后2阶.ARCH检验和White检验的原假设均为模型不存在异方差，由表5可知ARCH检验、White检验均在10%水平下接受原假设，故认为其不存在异方差性，无需建立自回归GARCH模型.最终模型估计结果如表6所示.

表6 模型最终回归结果

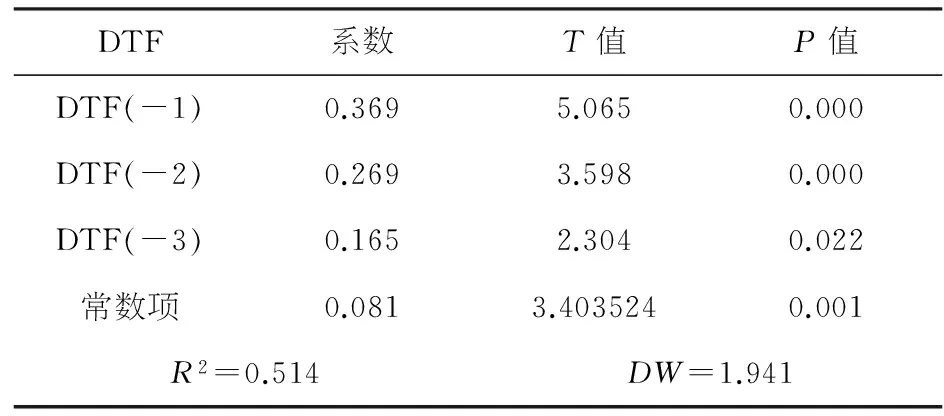
DTF系数T值P值DTF(-1)0.3695.0650.000DTF(-2)0.2693.5980.000DTF(-3)0.1652.3040.022常数项0.0813.4035240.001R2=0.514DW=1.941

由于对模型残差的异方差分析未发现异方差性，不存在建立GARCH模型的基础.因此不对自回归模型中的价差波动进行估计，只得到均衡价差的估计值如表7所示.

表7 自回归模型预测结果

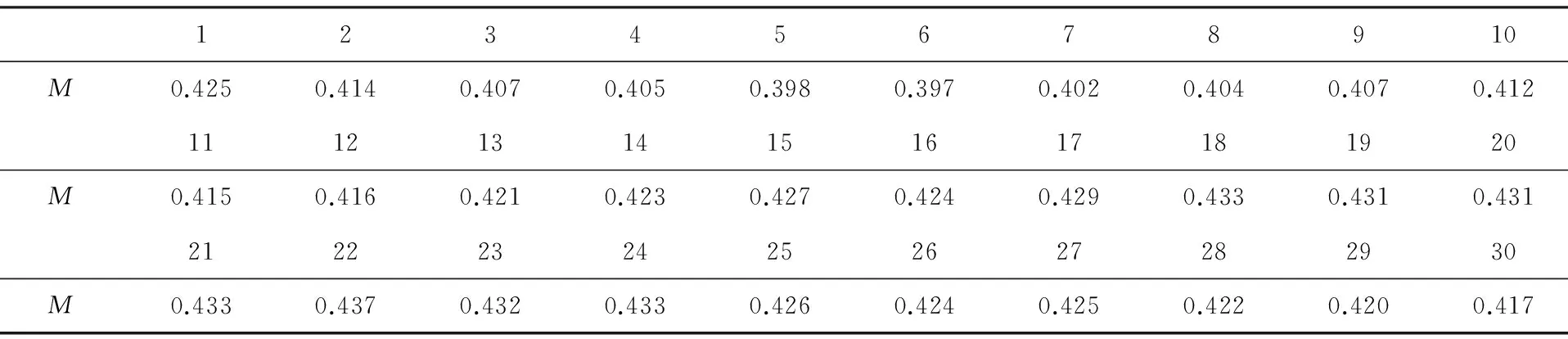
12345678910M0.4250.4140.4070.4050.3980.3970.4020.4040.4070.41211121314151617181920M0.4150.4160.4210.4230.4270.4240.4290.4330.4310.43121222324252627282930M0.4330.4370.4320.4330.4260.4240.4250.4220.4200.417

2.2 预测结果检验与最优预测模型

2.2.1 各模型预测结果检验

三个模型的均衡价差和价差波动估计值已经全部得出，现在对这些估计值与实际值进行比较，以判定模型的优劣.

1) 无偏性.在实际检验中，可以将估计值序列与实际值序列进行回归，通过观察回归系数和模型拟合优度来判定原估计无偏性.

2) 有效性.我们可以用均方差(MSE)来对估计的有效性进行类似的评判.MSE的概念如下：

3)相合性.相合性要求当估计次数无穷大时，估计值依概率收敛于真实值.本文中用均差(ME)和绝对均差(MAE)来进行类似的反映，ME和MAE的概念如下：

显然ME和MAE越小，估计越精确.

三个模型均得到了均衡价差，分别对他们按照式yt=c0+c1*xt+ut进行无偏性检验，结果如表8所示.

表8 各均衡价差估计值无偏性检验结果

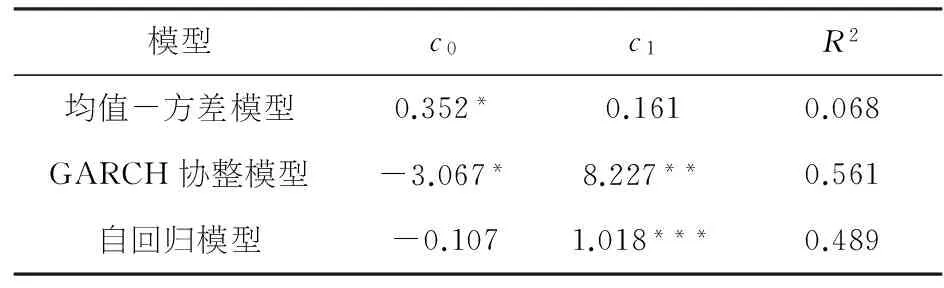
模型c0c1R2均值-方差模型0.352*0.1610.068GARCH协整模型-3.067*8.227**0.561自回归模型-0.1071.018***0.489

由表8可知，自回归模型估计值无偏性检验结果最好，均值-方差模型的估计结果无偏性质最差.

下面得到各模型的ME、MAE、MSE，结果如表9所示.

表9 各模型均衡价差估计值检验结果

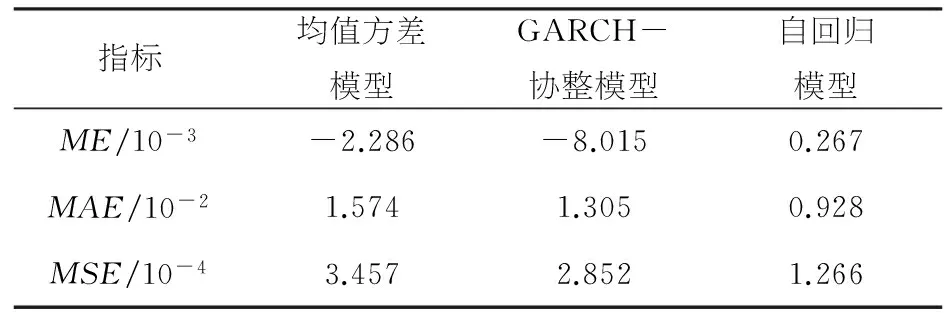
指标均值方差模型GARCH-协整模型自回归模型ME/10-3-2.286-8.0150.267MAE/10-21.5741.3050.928MSE/10-43.4572.8521.266

为了便于比较，ME、MAE、MSE按不同比例进行了放大.比较各模型，发现自回归模型的各项指标均优于其他模型.

2.2.2 最优国债期货跨期价差预测模型

根据以上预测选择自回归模型作为跨期价差均衡值的预测模型.具体公式如式(4)

Yt=α1yt-1+α2yt-2+…+αiyt-i+c

(4)

Yt即为均衡价差估计值，公式右侧滞后项的选择应在具体套利模型中选定.

在价差波动预测值检验中，GARCH模型的引入并没有提高预测值精度，均值方差模型预测出的方差在有效性(MSE)和相合性(ME、MAE)上全面优于GARCH协整模型.因此将均值方差模型中的预测方法作为最终方法，主要计算公式如式(5)所示，

σt=ln(DTFt/DTFt-1)

(5)

σ的平方即为价差波动方差，在最优模型中采用σ值的绝对值，取该绝对值10个样本点的移动平均值即得到最终的预测价差波动预测值.

经过对国债期货定价的研究发现国债期货跨期套利适合采用统计套利形式.从投资者角度来看，因尽早选用统计套利模型进行实际操作.本文所采用的价差预测模型充分合理.因此投资者可按照本文所选出的最优价差预测模型进行价差分析，并以此为基础建立套利策略进行套利.

[1] POOLE W. Using T-Bill futures to gauge interest-rate expectations [J]. Economics Review, 1978(Spr): 7-19.

[2] AGARWAL N, Madhogaria V, NARAYANAN S. Simulated trading-an analysis of pairs trading [R]. General Information, 2004.

[3] CORNELL B, FRENCH K R. The pricing of stock index futures [J]. Journal of Future Markets, 1983, 3(1): 1-14.

[4] CHOW B G, BROPHY D J. Treasury bill futures maket a formulation and reinterpretation [J]. Journal of Futures Market, 1982: 25-47.

[5] HEGDE S P, BRANCH B. An empirical analysis of arbitrage opportunities in the treasury bill Futures and Market [J]. Journal of Futures Market, 1985, 5(3): 407-424.

[6] CAPOZZA D R, CORNELL B. Treasury bill pricing in the spot and futures market [J]. The Review of Economics and Statistics, 1979, 61(4): 513-520.

[7] MACKINLAY A C, RAMASWAMY K. Index-futures arbitrage and the behavior of stock index futures prices [J]. Review of Financial Studies, 1988, 1(2): 137-158.

[8] HONG G, SUSMEL R. Pairs-trading in the Asian ADR market [R]. Saginaw Valley State University, 2003.

[9] SHANKEN J. The arbitrage pricing theory: Is it testable [J]. Journal of Finance, 2015, 37(5): 1129-1140.

[10] YADAV. Mean reversion in stock index futures mispricing: Evidence from the US and the UK [D]. Glasgow: Univeristy of Strathclyde, 1992.

[11] 康瑞强. 基于高频数据的期货统计套利研究[D]. 镇江: 江苏大学, 2009.

[12] ALEXANDER C, DIMITRIU A. Indexing and statistical arbitrage [J]. The Journal of Portfolio Management, 2005(2): 55-63.

[13] 陈彦晖. 基于ARMA-GARCH模型的恒指隐含波动率指数预测及其在期权交易中的应用[J]. 经济数学, 2014, 31(4): 27-35.

[14] 李雅晴. 国债期货推出前后市场利率定价机制探讨[J]. 商业时代, 2013(20): 66-67.

[15] 傅晓云. 国债期货在我国商业银行利率风险管理中的应用研究[J]. 新金融, 2013(10): 56-60.

Establishing national debt futures calendar spread model based on spread analysis

XU Qian-qian, XU Ji-xiao, YANG Jun-feng

(School of Business, Hohai University, Nanjing 211100, China)

Arbitrage and calendar spread arbitrage are the main investment method in the early month of bond futures trading. Predict inter-temporal spreads is the base of calendar spread arbitrage, which was ignored by many research about stock index futures and bond futures inter-temporal arbitrage before. This paper summarized the mean variance model, co-integration GARCH model two inter-temporal price forecast model, besides, this paper put forword that spreads autoregressive model also can do a very good prediction.This paper compared the predicting outcomes of each model, obtained of the optimal prediction model based on the regression model.

treasury bond futures; inter-temporal spreads; calendar spread arbitrage; autoregressive model; empirical analysis

2015-11-03.

国家自然科学基金基金(71271107)

徐倩倩(1990-)，女，硕士，研究方向：人力资源.

F724

A

1672-0946(2016)06-0745-07