大尺寸螺旋桨空化引起桨叶非定常力的数值模拟

周军伟,梅 蕾,倪豪良

(哈尔滨工业大学(威海) 船舶与海洋工程学院，山东 威海 264209)

大尺寸螺旋桨空化引起桨叶非定常力的数值模拟

周军伟,梅 蕾,倪豪良

(哈尔滨工业大学(威海) 船舶与海洋工程学院，山东 威海 264209)

对某实桨在均匀流场中的空化现象进行模拟，采用基于混合网格的Ansys/CFX对流场进行求解，结果显示，由于所处位置的静压力不同，不同桨叶的空化程度差异显著，空化面积出现周期性变化；在空化初期，桨叶非定常力不明显，而随着空泡数的减小，桨叶非定常力幅度逐渐增大，说明实桨尺度对桨叶空化的激振力具有较明显的影响。

螺旋桨空化；桨叶非定常力；均匀流场；静压力差

螺旋桨工作时扰动来流，不可避免地引发噪声，尤其是当空化发生后，噪声明显提高。引起空泡噪声的主要因素有空泡的生成与溃灭[1]，以及空泡导致的桨叶表面压力脉动[2-5]。然而，空泡导致的桨叶表面压力脉动不仅直接辐射噪声，也会激励桨叶振动而引发桨叶振动噪声。但到目前为止，关于空泡引起的桨叶振动噪声少见报道。

目前，桨叶振动噪声问题的分析方法主要有2种：①考虑流场和桨叶之间的耦合作用，而忽略流场和声场的耦合作用[6-8]。事实上，由于流场和声场的特征速度相差较大，这样的处理是合理的。②对流场、声场及桨叶响应单独进行分析[9-15]。这种方法仅适用于桨叶所受非定常力的频率与桨叶固有频率相差较大的情况。为此，本文即从流场和桨叶的单独响应分析出发,考虑到实际中大尺寸的螺旋桨，其工作过程中由于不同深度位置的静压力差别较大，其桨叶空化程度可能会随螺旋桨转动发生周期性的变化，进而会引起桨叶上的非定常力的变化，对桨叶噪声产生影响，采用数值方法，模拟了一台实桨在空泡发生后的桨叶所受非定常力情况，并对其受力特征进行了分析，探讨了大尺寸螺旋桨桨叶位置静压力变化对桨叶非定常力的影响，对实桨空化噪声的研究提供基础。

1 桨模

所用的是一台直径3.55 m的螺旋桨，采用非等螺距设计，其0.75R处的螺距比为0.803。螺旋桨外观见图1，其桨叶几何参数见表1。

图1 桨模外观

r/RLchord/DLskew/DP/D0．180．1840．0000．7670．200．190-0．0030．7720．230．198-0．0060．7770．250．206-0．0100．7830．280．215-0．0140．7880．300．223-0．0170．7920．350．239-0．0240．8010．400．256-0．0300．8100．500．288-0．0380．8200．600．315-0．0350．8180．700．329-0．0150．8110．750．3310．0010．8030．800．3250．0210．7890．850．3090．0460．7680．900．2810．0740．7370．950．2340．1050．7030．980．1840．1210．6850．990．1280．1320．674

注：Lchord-弦长；Lskew-翼型偏离弦向中点的距离。

为了方便数值模拟，其几何模型进口端也采用了导流罩的设计。

2 计算设置

为了模拟实际的螺旋桨工作环境，即桨叶在最上方位置时的环境压力较低，而在最下方位置时的环境压力较高，计算中计入了位置的影响。螺旋桨转轴沿水平方向，不同深度h下的环境压力按p=p0+ρgh计算。由于桨叶的浸深在转动过程中随时间不断变化，其空化程度也是不断变化的。计算中通过改变桨轴浸入深度来调整空泡数。

整个流域网格分为无穷远处的静止域和螺旋桨周围的转动域2部分，通过滑移面连接。桨叶表面采用混合网格，见图1，其在导边、随边、桨梢和根部导圆位置采用结构化网格，而在桨叶表面和轮毂表面采用非结构网格，这样能够保证在较少的网格数下实现对边缘流动的更精确模拟。桨叶表面第一层网格设置为10-5。静止域和转动域的整体网格见图2。在定常情况下的计算性能和实验性能的对比见图3，二者结果基本吻合。

图2 计算域的网格

图3 螺旋桨性能试验和数值模拟结果对比

为了分析不同空泡数下的桨叶受力情况，螺旋桨在固定转速和进速下工作，转速为4.6 r/s，进速Va=8 m/s，此时进速系数J=0.49，推力系数kt=0.177，转矩系数kq=0.023，敝水效率ηo=60.0%。计算中首先是无限水深下的模拟，得到无空泡性能，而后逐渐减小桨轴浸深，得到不同空泡数下的流场和桨叶受力情况。不同桨轴浸深hs下的空泡数σ见表2。空泡数定义为

(1)

式中：p0按105Pa计；pv按3 280 Pa计；水的密度ρ为997 kg/m3。

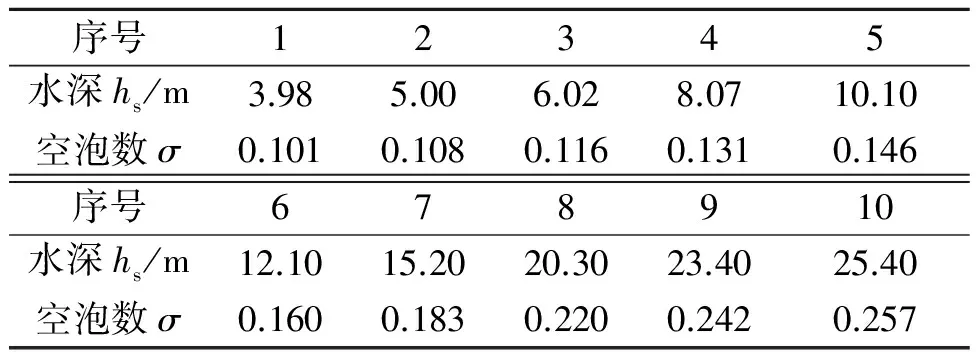
表2 桨轴浸深与对应空泡数

3 结果与分析

3.1 空泡数对性能的影响

不同空泡数下的螺旋桨推力系数kt和ηo效率见图4。可以看出，随着空泡数的增大，桨叶空泡现象将逐渐消失，但其推力并不是单调增加，而是存在一个最大推力点，该螺旋桨最大推力出现在σ=0.146的位置。这种现象与文献[16-17]的计算结果十分类似，其结果也在σ=0.183的位置出现一个效率最高点。出现这种现象的原因可能是空泡避免了桨梢吸力面压力的进一步降低，减小了叶背与叶面的压力差，从而减轻了绕流损失，而此时空泡本身引起的损失较小。而随着空泡的继续发展，空泡损失变得更大，螺旋桨性能开始降低。

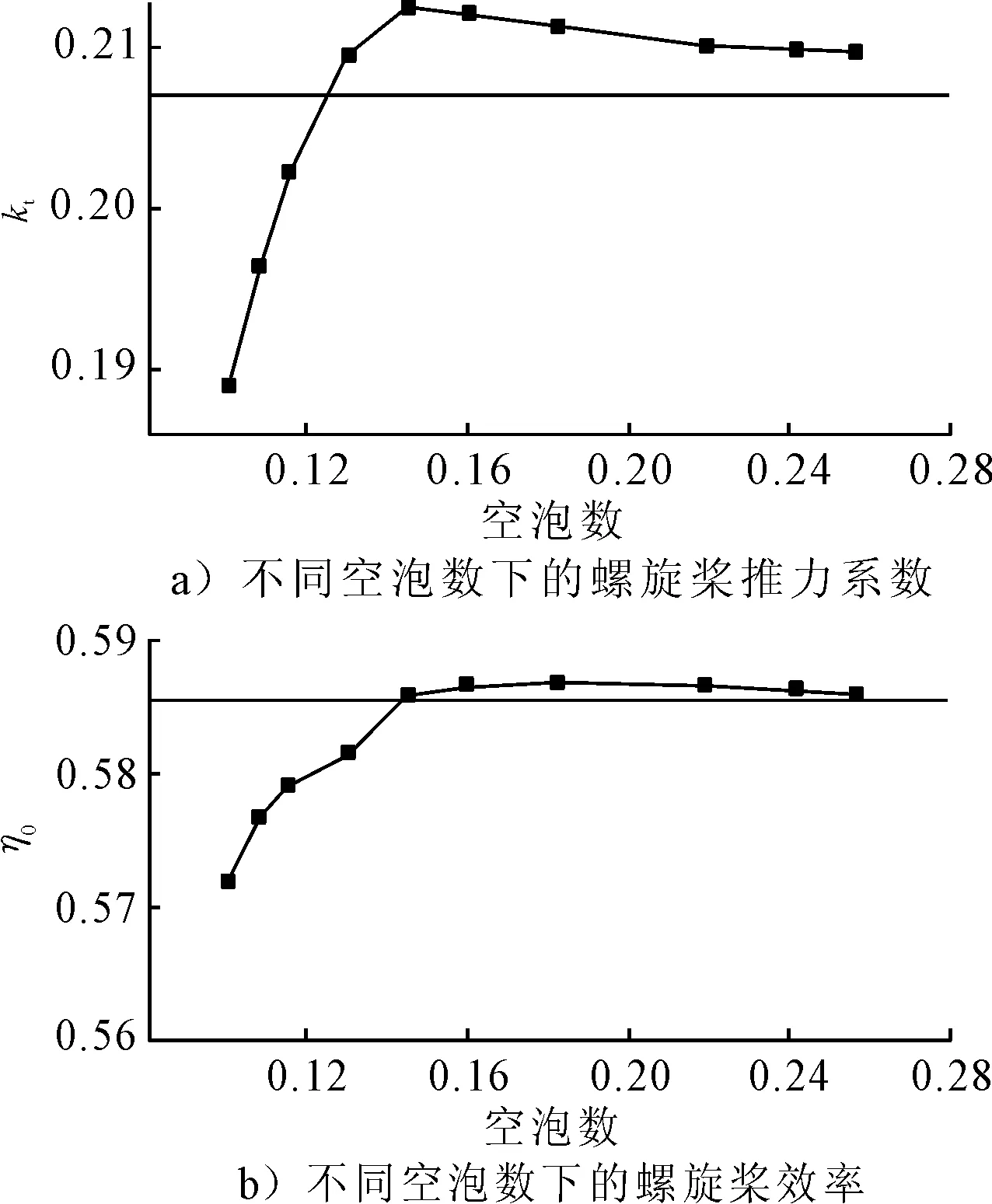
图4 J=0.49时不同空泡数下的推力系数和敝水效率

3.2 桨叶表面空泡情况分析

图5展示了空泡数σ=0.146时，处于不同位置的各个桨叶上的空泡面积，深色为空化区域，浅色为未空化区域。可以看出，0°桨叶浸深最小，其空化面积最大，而180°桨叶浸深最大，其空化面积最小。桨叶位置对实桨空化的影响十分明显。

图5 σ=0.146，J=0.49时桨叶吸力面的空泡区域

90°与270°桨叶虽然浸深相近，但二者并不完全对称，其空泡形状略有差别。各空泡数下不同位置的桨叶空化情况见图6。在空泡数较低的几个工况下，包括σ=0.108、σ=0.131、，90°与270°桨叶空化区域都有明显的差别，而在空泡数较大的几个工况下，包括σ=0.183、σ=0.257，二者的空化区域基本相同。

图6 不同空泡数下、不同位置桨叶上的空化情况

从图6中还可以看出，在较小空泡数的几个工况下，0°与180°桨叶的空化面积差别明显；而在较大空泡数的几个工况下，二者差别较小。从以上分析可以得出，重力对不同桨叶空化的影响主要发生在空泡数较低、空化现象较剧烈的情况下，而在空化起始阶段其影响较小。

3.3 激振力分析

3.3.1 幅度及周期分析

由于相同工况下每个桨叶的受力仅在相位上有所差别，图7a)仅列举了单桨叶在7个空泡数下的受力随时间的变化。从图7b)中可以看出，随着空泡数的降低，桨叶上的激振力幅度越来越大，平均值逐渐降低，而周期基本不变。与图6对比表明，桨叶上激振力随时间的变化基本与桨叶表面空化情况相对应。桨叶负荷受空泡面积的影响，在空泡数较小的情况下，桨叶表面空泡面积随转动变化明显，此时激振力较大，而在空泡数较大的情况下，桨叶表面空泡面积随转动变化不大，因而激振力较小。由此认为，当空泡数较小时，实桨在空化情况下所受激振力主要受位置静压力差的影响，而在空泡数较大时，其影响并不明显。

图7 不同空泡数下的单桨叶所受轴向激振力

3.3.2 频率分析

图8给出了σ=0.108与σ=0.146 2个典型情况下桨叶所受激振力的频谱分析，分别代表了较小空泡数和较大空泡数2种情况。从图8可以看出，2个情况下的激振力频率都主要集中在低频段，且频率与桨叶转动频率一致。图8b)中还存在1个高频激振力，这可能是流场中湍流或非定常涡引起的。此外，图8a)中仅存在1个频率，这表明桨叶受力几乎是正弦的，而图8b)中存在1个二阶频率，更高阶频率则不明显。

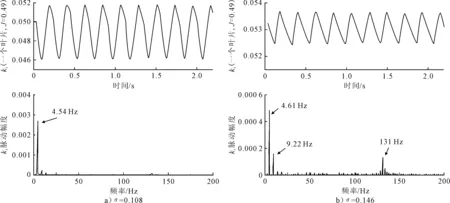
图8 不同空泡数下桨叶所受激振力的频谱分析

3.3.3 合力分析

以上分析的都是空化时桨叶轴向受力的变化情况，而在实际情况中，单个桨叶是在所受合力的作用下发生振动的。为了对比单桨叶所受合力与轴向力随时间的变化特点，给出4个空泡数下的对比见图9。可以看出，单桨叶所受合力的变化趋势与幅度与轴向力基本一致，二者仅在平均值上有所差别，这也反映了桨叶所受激振力主要是轴向力分量的影响。

从图9中还可以看出，随着空泡数的增加，二者的平均值差值逐渐增大。由于桨叶受合力是轴向力和切向力的合成，可见随着空泡数的增大，空泡对切向力的影响逐渐减小，切向力的恢复比轴向力要快，这一点也可以从图4中效率逐渐提升的趋势上看出。

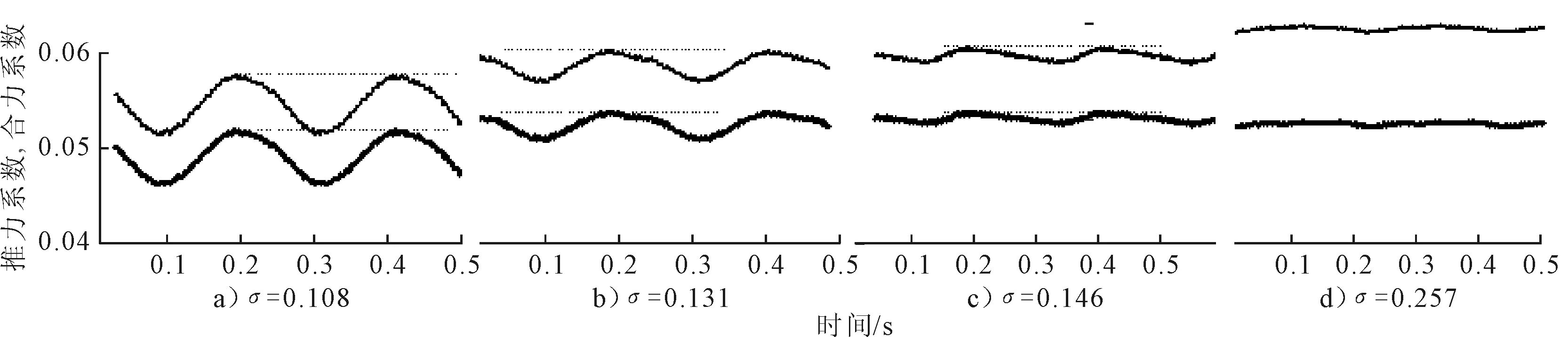
图9 轴向力(粗)与合力(细)的对比

对比图9中σ=0.108、σ=0.131与σ=0.146三个工况的桨叶受力变化曲线可以发现，在较小空泡数时，如σ=0.108，桨叶受力变化曲线近似为正弦曲线，即推力变化仅与所处位置有关；而在σ=0.131和σ=0.146，从图9能够明显看出，推力增加较快而降低较慢，曲线不再是正弦曲线，这说明推力不完全由所处位置决定。由于推力大小与空泡面积相关，可以推断空泡面积不完全由桨叶所处位置决定，或者说在螺旋桨转动过程中，空泡面积的变化具有一定的迟滞性。

螺旋桨整体受力变化见图10。由图10可见，螺旋桨整体受力基本不变，即空泡对螺旋桨轴的非定常力作用很小。

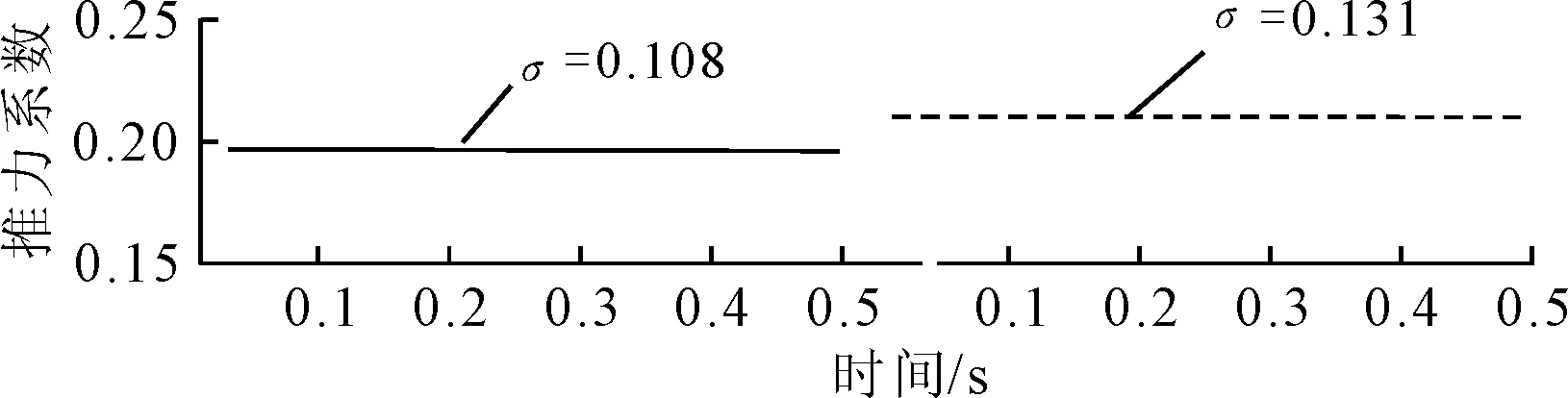
图10 螺旋桨全桨轴向力随时间的变化

4 结论

1)桨叶位置静压力差对桨叶激振力有明显影响，主要发生在空泡数较低、空化现象较剧烈的情况下，而在空化起始阶段其影响较小。

2)单桨叶上轴向激振力振幅的变化基本与桨叶表面空化情况相对应，激振力频率都主要集中在低频段，且频率与桨叶转动频率一致。

3)单桨叶所受合力的变化趋势和幅度与轴向力基本一致，二者仅在平均值上有所差别，但该合力对螺旋桨桨轴作用很小。

本文仅针对某一大直径的实桨展开，结论可能存在一定局限性。今后将对系列尺寸的实桨进一步展开尺寸对桨叶空化非定常力的影响，并对其产生的噪声进行分析。

[1] 黄景全.空泡起始和溃灭阶段的噪声[J].应用数学和力学,1990,11(6):725-730.

[2] YE J M, XIONG Y, LI F, et al. Numerical prediction of blade frequency noise of cavitating propeller[J]. Journal of Hydrodynamics, Ser. B; 2012,24(3):371-377.

[3] SEOL H. Time domain method for the prediction of pressure fluctuation induced by propeller sheet cavitation: Numerical simulations and experimental validation[J]. Ocean engineering, 2013,72:287-296.

[4] 王顺杰,王易川,戴卫国,等.片空化状态下对转螺旋桨噪声特性仿真分析[J].船舶力学，2014,18(7):778-785.

[5] KEJR Y Z , KAP J H. Numerical prediction of the blade rate noise induced by marine propellers[J]. Journal of ship research, 2004,48(1):1-14.

[6] 吴思远,黎胜.船用螺旋桨叶片振动辐射噪声数值分析[J].振动与冲击，2014,33(12):207-210.

[7] 于大鹏,赵德有.螺旋桨鸣音的混沌动力特性研究[J].振动与冲击，2009,28(12):47-52.

[8] ZHOU Q, XIE J, FANG B, et al. Parametric study of propeller tone noise due to nonuniform flows[J]. Journal of computational acoustics, 2013,21(3):1-18.

[9] 郑小龙,王超,张立新,等.非均匀流场中螺旋桨水动力及噪声特性预报研究[J].武汉理工大学学报：交通科学与工程版，2014,38(6):1300-1307.

[10] 黄振宇.螺旋桨的非定常力计算[C].第九届全国水动力学学术会议暨第二十二届全国水动力学研讨会文集，2009.

[11] 何汉保,张有庆,夏飞.潜艇艉部伴流场、螺旋桨激振力研究[J].舰船科学技术，1995(5):16-26.

[12] SONG Y B, WEN J H, YU D L, et al. Reduction of vibration and noise radiation of an underwater vehicle due to propeller forces using periodically layered isolators[J]. Journal of sound and vibration, 2014(14):3031-3043.

[13] XIA P P, GUI H B, HU ZK, et al. The effect of the excitation position on the sound radiation of propeller[C]. SUTTC, 2013:82-86.

[14] 王冠,张科.螺旋桨桨叶模态试验分析[J].声学技术，2014,33(S1):151-154.

[15] 范永忠,孙康,吴人洁.环氧树脂基复合材料的阻尼性能及在降噪上的应用研究[J].材料工程，2000(3):29-35.

[16] RHEE S H, KAWAMURA T, LI H Y. Propeller cavitation study using an unstructured grid based Navier-stoker solver[J]. Transactions of the ASME. I: Journal of fluids engineering, 2005,127(5):986-994.

[17] 朱志峰,王晓燕,方世良.基于非结构网格RANS方法螺旋桨空化研究[J].海洋工程，2009,27(4):103-107.

Simulation of Unsteady Force on Blade Induced by a Scaled Propeller Cavitation

ZHOU Jun-wei, MEI Lei, NI Hao-liang

(School of Naval Architecture and Ocean Engineering, Harbin Institute of Technology (Weihai), Weihai Shandong 264209, China)

The cavitations phenomenon of a real propeller in a uniform flow field was simulated, in which the convection field is solved by Ansys/CFX based on the hybrid grid. The results showed that the cavitation area of the propeller blades varies periodically with the static pressure at different position. At the early stage of cavitation, the unsteady force on blade is not obvious, but with the decrease of cavitation number, the unsteady force amplitude increases gradually. So the size of the real propeller has a significant effect on the exciting force of the blade cavitation.

propeller cavitations; unsteady force on blade; uniform flow; static pressure difference

10.3963/j.issn.1671-7953.2016.06.004

2015-12-18

国家自然基金(51309070)； 山东省科技厅项目(2013GGA10065)

周军伟(1981—)，男，博士,副教授

U661.31；U664.33

A

1671-7953(2016)06-0015-05

修回日期：2016-05-26

研究方向:船舶推进器性能研究、叶轮机设计及分析

E-mail:zhou_junwei@foxmail.com