敏捷光学卫星无控几何精度提升途径探讨

李贞 金涛 李婷 杨冬

(北京空间飞行器总体设计部，北京 100094)

敏捷光学卫星无控几何精度提升途径探讨

李贞 金涛 李婷 杨冬

(北京空间飞行器总体设计部，北京 100094)

针对敏捷光学卫星无控制点几何精度，提出了区分高频和低频姿态误差、同时考虑定位误差的精化传播模型，通过仿真分析得出了低频姿态误差及姿态稳定度误差对定位精度的影响规律，并以满足30 m平面定位精度和1：50 000比例尺测图要求为例，进行了定位误差分配和定位精度预估，提出了提高无控定位精度的措施。结果表明：星敏感器低频姿态角误差主要造成了水平位置方向的系统误差，但其在高程位置方向的系统误差可以通过卫星前后对称俯仰成像进行消除。当定位精度要求30 m量级时，星敏感器低频误差和夹角稳定性不需要在现有卫星水平上加严控制，但是应尽量采用大基高比，同时采用异侧对称立体成像方式，避免系统性低频姿态误差带来额外的高程误差；当精度要求满足1：50 000时，应配置0.9″精度星敏感器，200 Hz以上高频姿态测量设备和在轨夹角检测装置，同时将低频误差有效控制在5″以内等，以满足15 m平面，6 m高程的精度要求。

敏捷光学卫星；无控制点；定位精度；低频误差；姿态内插；姿态稳定度

1 引言

近年来，我国陆续发射了多颗高分辨率光学卫星，影像分辨率逐渐从米级提升到亚米级，同时，借助整星大范围、敏捷机动能力，能通过沿轨道方向前后摆动获取同轨立体像对，具备了实现大比例尺测绘的必要条件。但是，相比国外高几何精度的商业遥感卫星，国产遥感卫星所能实现的几何精度仍在几十米量级[1]，利用国产高分辨率遥感卫星进行立体成像测绘亦处于尝试阶段。

从原理上说，无地面控制点卫星高精度几何定位是完全可行的，但在工程实现方面，我国卫星，尤其是敏捷卫星要实现10 m以内定位精度要求并不容易，关键问题：①星敏感器测定的姿态角误差除标称高频测量误差外，还有不可忽视的低频误差以及相机与星敏感器间的夹角稳定性误差。在具体地面无控制点处理中，一般无法用平差予以消除，导致处理成果带有额外的误差。②不同于采用固定交会角的多线阵测绘卫星，敏捷卫星为实现立体成像，姿态机动角度大且频繁，卫星姿态稳定度较差，而星敏感器、陀螺输出姿态数据频率较低，卫星姿态往往带有很大的随机误差，也会直接影响图像定位精度。

对于卫星的图像定位精度分析问题，文献[2]利用摄影测量几何关系对无控制点条件下的卫星摄影测量高程误差进行了带有物理含义的理论估算；文献[3]利用前方交会原理建立了误差数值模型，研究了单线阵CCD相机立体定位中姿态角、摄站位置、内方位元素几何标定误差以及像点量测误差等对定位精度的影响规律，这些文献仅考虑了各参数的随机误差。文献[4]综合分析了影响定位精度的各个指标的随机和系统误差，但针对“随机+系统”误差的传播特性未进行区分，也未对涉及姿态稳定度误差的关键设计参数要求进一步细分。

本文假定卫星在轨后，地面处理系统已完成对线阵CCD相机的在轨内标定和安装矩阵等外标定工作，进一步探讨星敏感器低频误差和敏捷姿态不稳两个问题对无地面控制点图像定位精度的影响规律及其误差消除措施，提出了区分高频和低频姿态误差、同时考虑设计参数的定位误差精化传播模型，通过仿真分析得出了低频角元素误差及姿态稳定度误差对定位精度的影响规律，以满足30 m平面定位精度和1：50 000比例尺测图要求为例，进行了定位精度指标分析，最后提出了提高无控定位精度的措施。

2 敏捷光学卫星姿态误差特性

从我国资源三号卫星发射入轨并成功应用之后，后续研制的非测绘类国产卫星几何定位精度也有了较大的提升，主要原因在于卫星均采用了星地一体化设计，如高精度授时系统、相机/星敏感器等温一体化安装，同时在轨几何检校水平也在不断地提升[1,5]。但是，星上测姿系统误差往往受星敏感器性能影响，并随卫星工作模式不同而呈现新的特点。

总结当前敏捷光学卫星的姿态误差规律，主要有：

(1)低频误差，包括星敏感器慢漂和星敏感器与相机间的夹角缓变，这两种误差难以区分，均呈现周期性特点。根据在轨星敏感器夹角数据，在一个轨道周期内，星敏感器夹角变化量级达60″，但在一个基线内近似表现为单调、线性的系统误差特性[2-3,6]；

(2)高频误差，敏捷光学卫星具有 “动中成像”特点，即为实现高频次成像，不再像传统遥感卫星那样以极高的卫星姿态稳定度成像。这种工作模式造成的姿态“高频误差”，其幅值较低，频率从几十赫兹到百赫兹量级，最终会引起姿态内插精度的下降。

3 敏捷光学卫星无控制点定位误差传播模型

3.1 空间前方交会原理

图1给出了单线阵立体摄影及定位的原理示意图。假设M(X,Y,Z)为地面目标点，Sl,Sr,Sr′分别为目标点M在多次成像中对应的像点，其中，Sl与Sr两次成像构成同侧立体成像，Sl与Sr′两次成像构成异侧立体成像。若立体影像的轨道位置与姿态已知，那么根据像点坐标就可以确定这两条空间直线的交点，即地面点的位置是唯一可确定的。从中可以看出，立体定位的数学基础是空间前方交会。

采用投影系数法进行空间前方交会，通过对误差项进行微分，可得到单线阵CCD相机的定位误差方程[7-8]。

(1)

式中：dX，dY，dZ为目标点M的地面坐标误差；dXsl,dYsl,dZsl,和dXsr,dYsr,dZsr分别为前、后视摄站的地面坐标误差；dXcl，dYcl，dZcl和dXcr，dYcr，dZcr分别为目标点M在前、后视像点的空间坐标误差；dBy为摄影基线在Y方向的误差分量；Nl，Nr和dNl，dNr分别为前、后视像点投影到地面上点的投影系数及其误差。

图1 立体观测原理示意图
Fig.1 Stereo mapping diagram

3.2 系统和随机姿态误差的联合传播模型

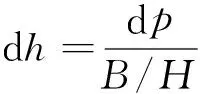
令ω,φ,κ为卫星滚动、俯仰和偏航3个姿态角元素，其误差dω,dφ,dκ可表示为式(2)的形式。

(2)

式中：dωl,dφl,dκl和dωr,dφr,dκr分别为前、后视星敏感器姿态测量误差，ml,nl,ol和mr,nr,or分别为前、后视星敏感器姿态测量误差系数。

以dω为例，由于dωl和dωr均包含高频中误差σ(独立的随机误差)和低频中误差ε(系统误差)，根据误差传播理论[10]，星敏感器姿态测量误差dω对定位中误差的传播规律为

(3)

高频随机姿态误差和低频系统姿态误差对定位精度的影响可以用图2表示，由图2可知：

(1)对于高频随机姿态误差，前后视姿态误差之间存在相对误差Δσ，对平面和高程均产生误差，如图2(a)所示。

(2)对于低频系统姿态误差，当卫星采用异侧立体观测，误差系数ml和mr的符号相反，从而对高程误差产生相消的结果，如图2(b)所示； 对于同侧立体观测，误差系数ml和mr的符号相同，从而对高程误差产生累加的结果，如图2(c)所示；对平面则均产生误差。

根据资源三号卫星的设计参数[9]，采用本文误差分析模型可知，星上应存在6″左右的缓变系统性姿态误差，这种误差通过一次在轨标定很难去除。

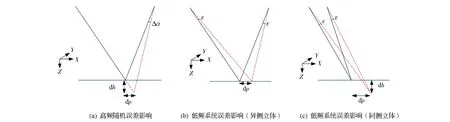
图2 高频和低频误差对定位精度影响示意图Fig.2 High-frequency and low-frequency errors applying to the locating diagram

3.3 考虑设计参数的姿态稳定度误差模型

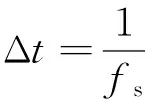
(1)当卫星姿态不存在高频大幅值变化时，可以用线性内插进行插值；

(2)姿态角速度误差短时间内可以用卫星姿态稳定度表征。

成像任意时刻ti对应的姿态可表示为

(4)

式(4)的误差方程为

(5)

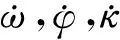
从式(5)可以看出，卫星任意行插值姿态精度与卫星姿态稳定度及测姿频率相关。当不满足两个前提时，则会产生“高频姿态误差”。为此，敏捷光学卫星应尽可能通过星上隔振措施降低振动幅值，同时采用高频高精度测姿设备对姿态抖动进行测量。

4 误差规律分析与验证

4.1 仿真参数

下文对姿态测量误差及姿态稳定度、测量姿态输出频率等因素分别进行分析。为了便于讨论和仿真分析，根据当前技术和硬件发展水平，设定一组参数，如表1所示。

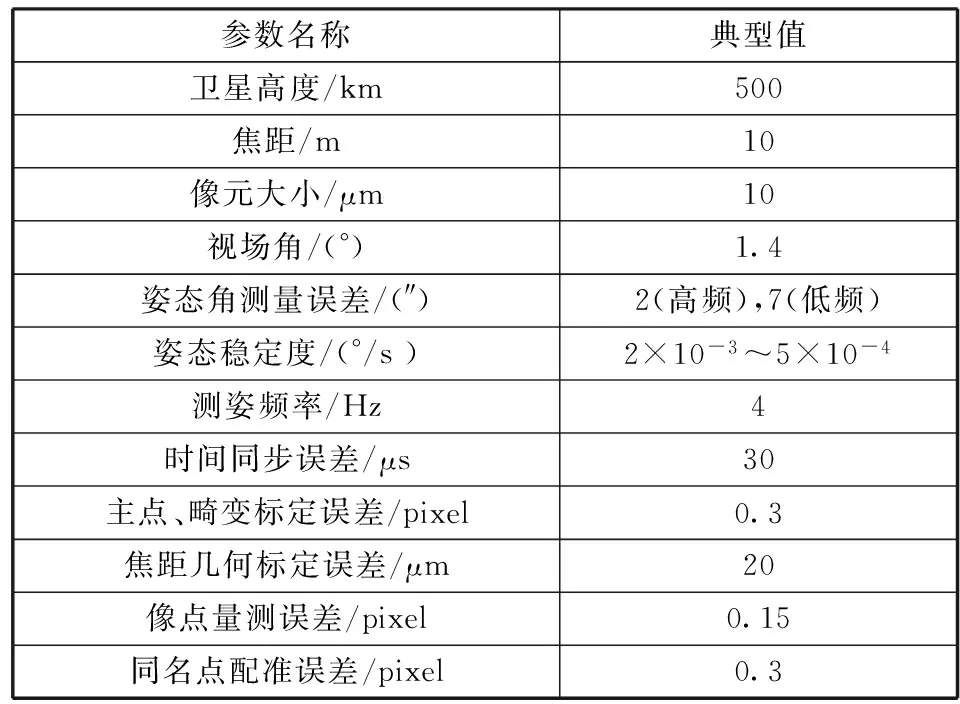
表1 卫星参数及误差典型值

4.2 不同交会条件下低频误差对定位精度的影响规律

下面根据表1 参数，改变低频误差值，保持其他误差不变，可得到低频误差对定位精度的影响规律。

从图3～图5可以看出：

(1)随着姿态低频误差的增大，平面定位误差随之增大；

(2)姿态低频误差对高程误差的影响则根据立体观测模式的不同有不同的影响规律：①对于对称式的异侧立体成像，低频误差对高程误差几乎无影响；②对于非对称式异侧立体成像，低频误差对高程误差存在缓慢增长影响；③对于同侧立体成像，低频误差对高程误差则有着类似于平面误差一样的影响。

这与式(3)的理论分析是一致的。

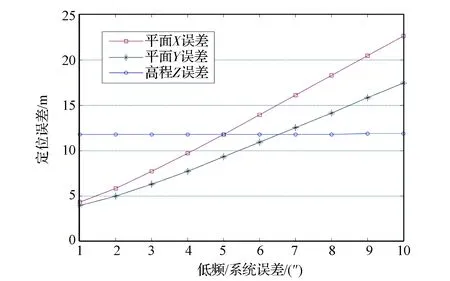
图3 异侧对称立体(前视15°，后视-15°)观测下低频误差对定位精度的影响规律Fig.3 Influence law of low-frequency error(forward-looking 15°and backward-looking -15°)on the locating accuracy by the side symmetric stereo imaging

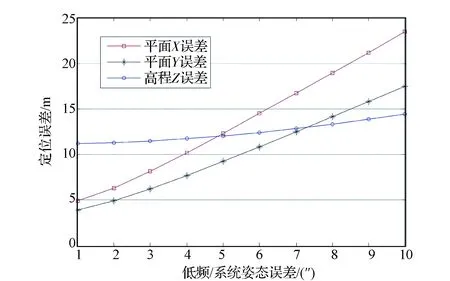
图4 异侧非对称(前视25°，后视-5°)立体观测下低频误差对定位精度的影响规律Fig.4 Influence law of low-frequency error (forward-looking 25° and backward-looking -5°) on the locating accuracy by the side asymmetric stereo imaging

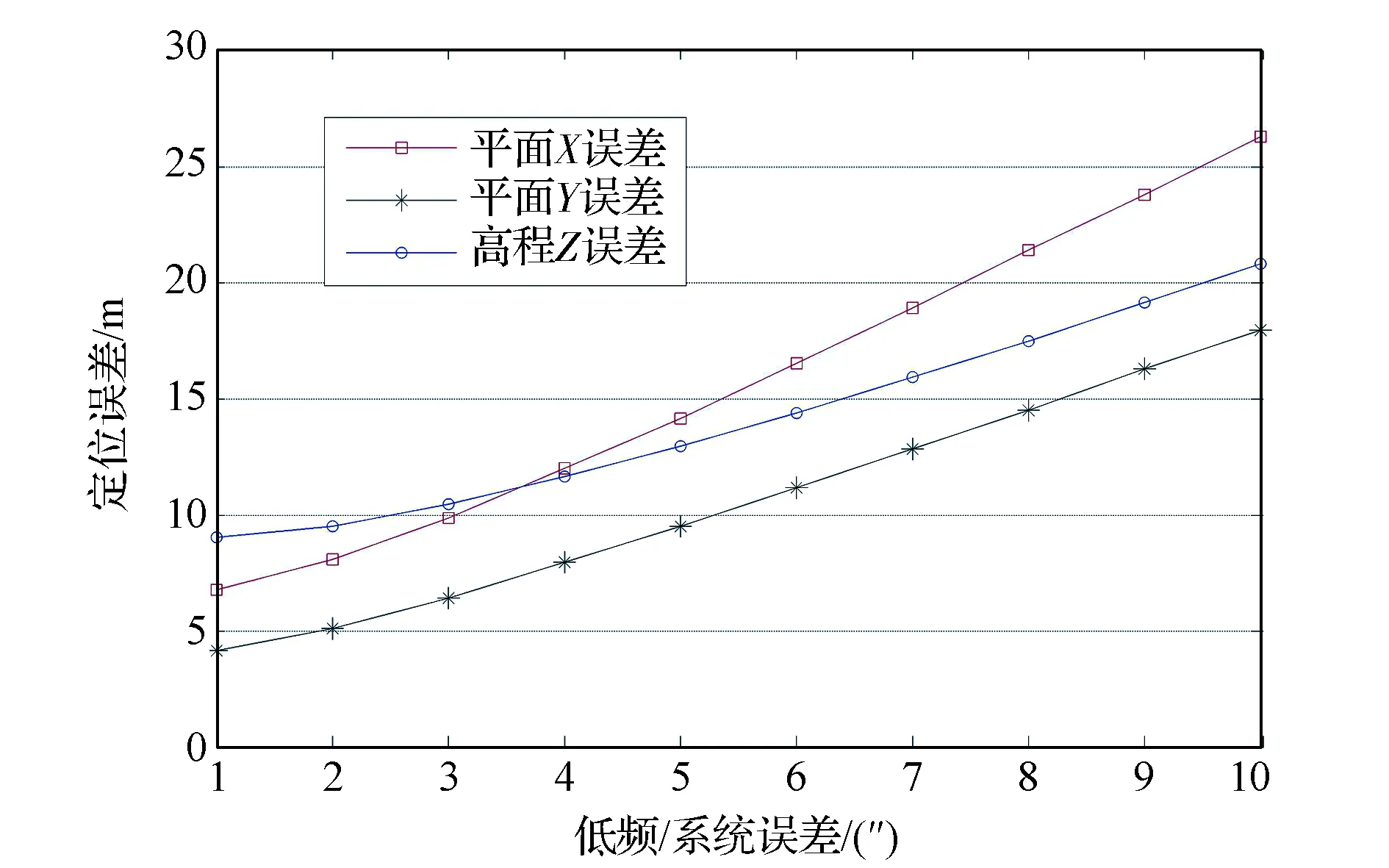
图5 同侧立体(前视35°，后视5°)观测下低频误差对定位精度的影响规律Fig.5 Influence law of low-frequency error (forward-looking 35° and backward-looking 5°) on the locating accuracy by the stereo imaging on the same side

4.3 不同姿态输出频率下姿态稳定度对定位精度的影响规律

根据表1 参数设置，利用本文定位精度评估模型，图6给出了基高比为0.53(俯仰±15°)，改变姿态稳定度误差值，保持其他误差值不变时，对定位精度影响规律。从图6中可看出，随着卫星姿态稳定度的下降，定位精度也下降，尤其是高程误差受姿态稳定度影响较大。

根据式(5)，在姿态稳定度不佳的情况下，增加星敏感器的测量频率或者配置高精度的高频率的相对姿态测量设备，可实现姿态测量精度不变但以更高姿态测量频率提高每行数据的姿态精度，从而提高定位精度(但值得说明的是，当星上存在微振动时，则必须以高于其特征频率的测姿设备才能复原出姿态的抖动)。

图7为卫星姿态稳定度为0.01(°)/s条件下，不同测姿频率下的定位误差规律，可以看出：随着测量姿态输出频率的提高，对定位精度提升的幅度高程Z>平面XY，当整星测姿频率为32 Hz时，其高程定位精度相比4 Hz提高了约75%，然而当测姿频率不断提高至200 Hz甚至10 000 Hz时，定位精度趋于稳定。

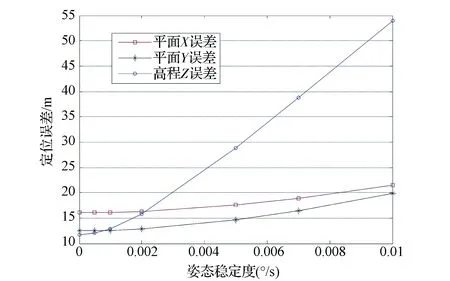
图6 姿态稳定度对定位精度影响规律(4 Hz测姿)Fig.6 Influence law of attitude stability on the locating accuracy (4 Hz attitude measuring)

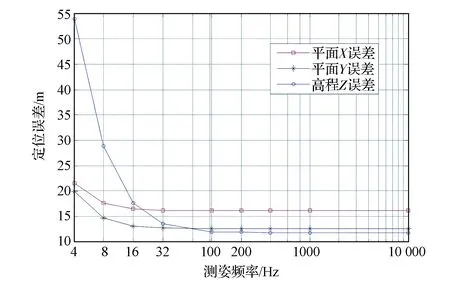
图7 测姿频率对图像定位误差的影响规律(姿态稳定度为0.01 (°)/s时)Fig.7 Influence law of attitude measuring frequency on the locating accuracy (attitude stability： 0.01(°)/s)

5 无控制点图像定位误差分配及精度预估

5.1 误差分配方案一

根据本文提出的定位精度预估模型，可以得到在表1 参数和误差水平下的卫星无控制点定位精度，如表2所示。数据显示：当平面定位精度要求30 m量级时，星敏感器低频误差和夹角稳定性不需要在现有卫星水平上加严控制，但是应尽量采用大基高比异侧立体成像方式，避免系统性角元素误差带来额外的高程误差。

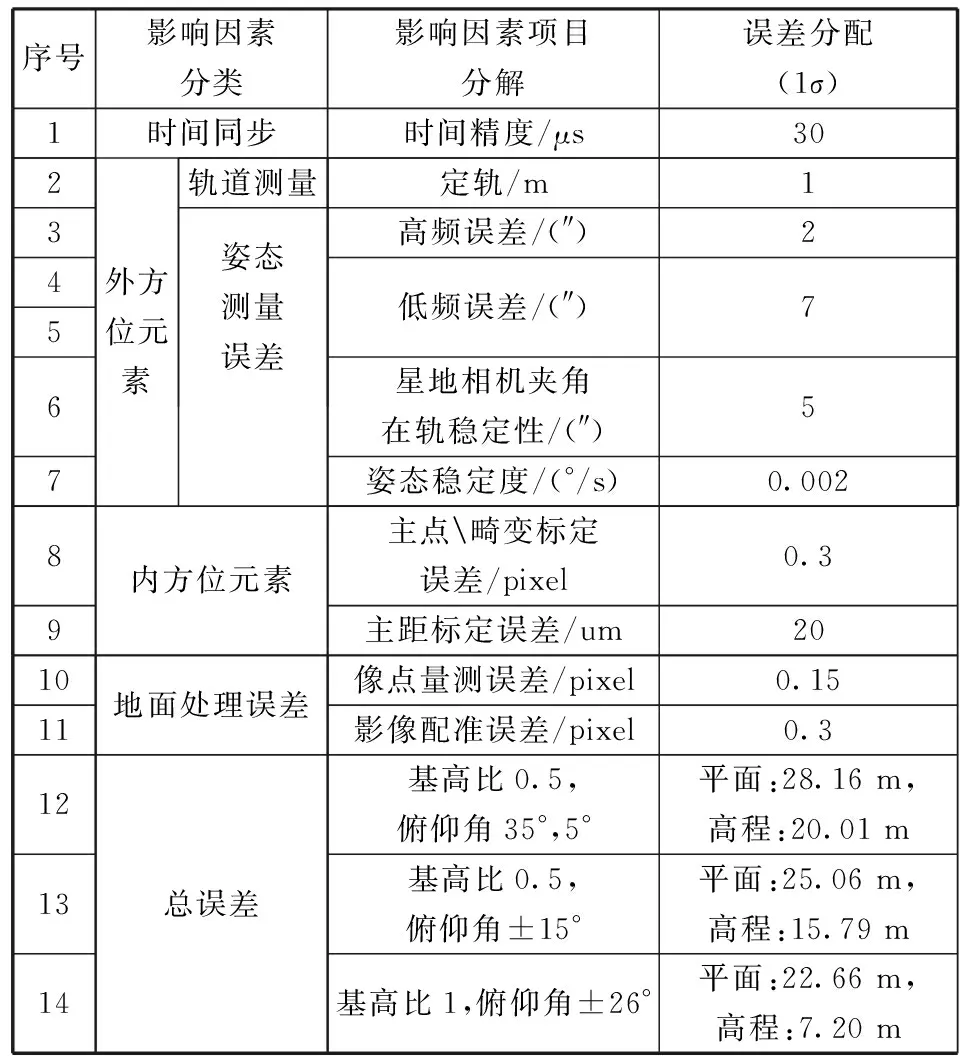
表2 无控制点图像定位误差预估(方案一)

5.2 误差分配方案二

为了满足1：50 000比例尺测绘制图的定位精度(平面15 m，高程6 m(1σ)[7])要求，可采取如下措施：

(1)采用甚高精度高频角位移测量设备实现高频、高精度姿态测量，如日本先进对地观测卫星(ALOS)采用三台高精度的星敏感器(9″，3σ)结合惯性陀螺和附加的高精度(均方根误差0.01″)角位移测量传感器，通过联合姿态确定算法，使卫星的姿态确定精度达到了在轨处理为1.08″，地面事后处理为0.5″的水平[11]。同时，测姿频率实现大于200 Hz，可消除姿态稳定度不高引起的误差。

(2)采用高精度夹角记录装置对星敏感器/相机夹角进行在轨测量。为了保证在轨无控定位精度要求，采取在轨实时测量方法，对相机与星敏感器视轴间夹角变化测量。地面处理时利用在轨测量数据对夹角相对几何关系进行标校，减小基准转换过程中引入的误差。

通过表3误差分配和定位精度预估可知，采用以上两个途径，星敏感器高频误差满足0.9″，低频误差有效控制在5″以内，即可以实现1：50 000比例尺的测绘制图的定位精度。

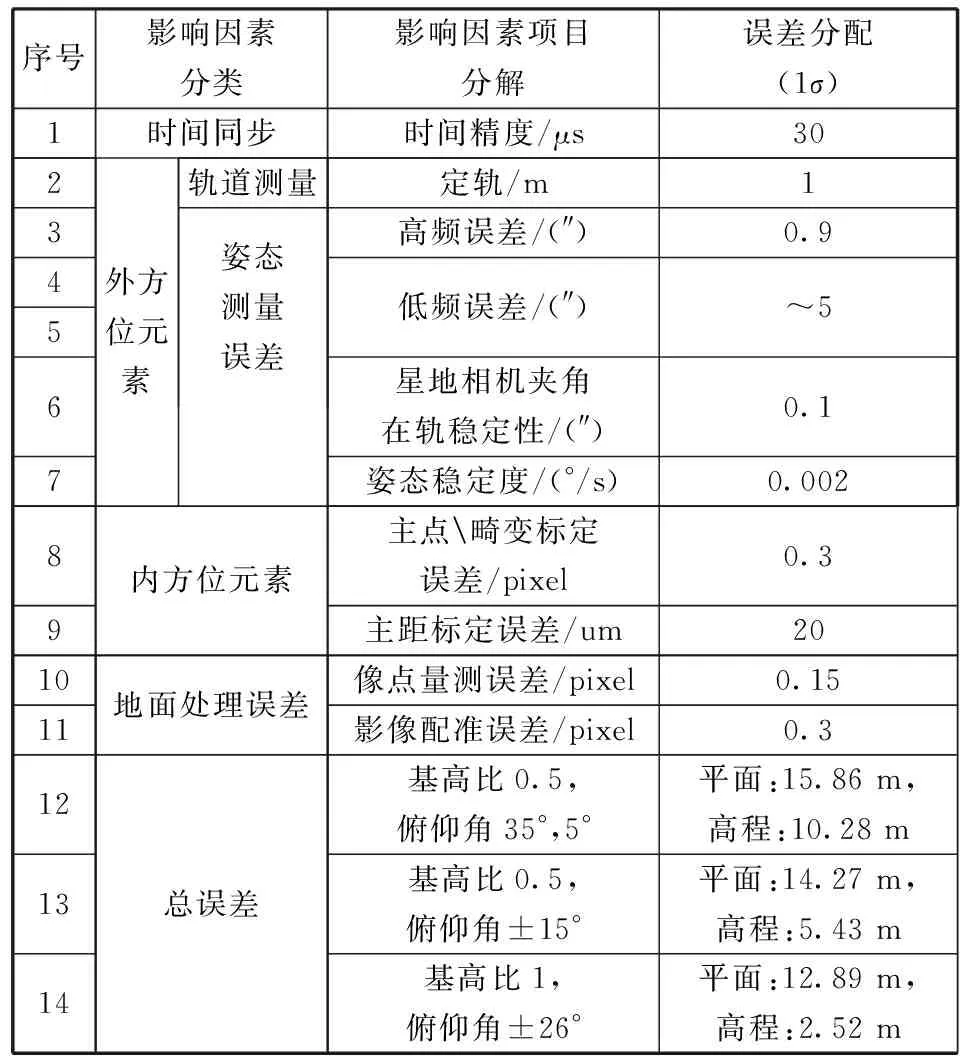
表3 无控制点图像定位误差预估(方案二)

6 结论

对于当前我国国产卫星的制造和设计水平的发展现状，影响定位精度的关键问题在于姿态角元素的低频和缓变误差以及因敏捷卫星稳定度下降带来的姿态插值精度下降。本文针对立体测绘中的姿态误差规律进行了分析，建立了区分高频和低频缓变误差、同时考虑设计参数的误差传播模型，进行了误差传播规律分析和定位精度指标分析。针对主要环节提出了相应措施。得出结论如下：

(1)当卫星采用异侧立体观测，前后视的低频缓变误差对高程误差产生相消的结果，而对于同侧立体观测，前后视的低频缓变误差对高程误差产生累加的结果。当前在轨测绘卫星如资源三号，星上应存在6″左右的缓变系统性姿态误差，这种误差通过一次在轨标定很难去除。

(2)在姿态稳定度不佳的情况下，限制星上微振动幅值、采用高精度相对测量设备并增加姿态测量频率可以提高每行数据的姿态精度，从而提高定位精度。随着测姿频率的提高，对定位精度提升的幅度高程Z>平面XY；当整星测姿频率为32 Hz时，其高程定位精度相比4 Hz提高了约75%，然而当测姿频率不断提高至200 Hz甚至10 kHz时，定位精度趋于稳定。

(3)当平面定位精度要求30 m量级时，星敏感器低频误差和夹角稳定性不需要在现有卫星水平上加严控制，但是应尽量采用大基高比异侧立体成像方式，避免系统性低频姿态误差带来额外的高程误差。当精度要求满足1：50 000时，可以通过采用高频姿态测量设备和夹角检测装置两种措施，同时将低频误差有效控制在5″以内，以满足测绘要求。

References)

[1]李德仁，张过，蒋永华，等，国产光学卫星影像几何精度研究[J].航天器工程，2016，25(1)：1-9

Li Deren,Zhang Guo,Jiang Yonghua,et al. Research on image geometric precision of domestic optical satellites [J]. Spacecraft Engineering,2016,25(1):1-9 (in Chinese)

[2]王仁享，胡莘，王建荣.天绘一号无地面控制点摄影测量[J].测绘学报,2013，42 (1):1-5

Wang Renxiang,Hu Xin,Wang Jianrong. Photogrammetry of mapping satellite-1 without ground control points[J]. Acta Geodaetica et Cartographica Sinica,2013，42(1):1-5 (in Chinese)

[3]王任享，王建荣，胡莘.在轨卫星无地面控制点摄影测量探讨[J]．武汉大学学报·信息科学版，2011，36(11)：1261-1264

Wang Renxiang,Wang Jianrong,Hu Xin. Photogrammetry of in-flight satellite without ground control point [J]. Geometrics and Information Science of Wuhan Univer-sity,2011，36(11)：1261-1264 (in Chinese)

[4]夏中秋，黄巧林，何红艳，等.高分辨率光学遥感卫星集合链路定位精度分析[J].航天返回与遥感，2016，37(3)：111-119

Xia Zhongqiu,Huang Qiaolin,He Hongyan,et al. Analysis of geolocation accuracy of high resolution optical remote sensing satellite geometric chain[J]. Spacecraft Recovery & Remote Sensing,2016,37(3):111-119 (in Chinese)

[5]金涛，李贞，李婷,等.提高光学遥感卫星图像几何精度总体设计分析[J].宇航学报，2013，34(8)：1159-1165

Jin Tao,Li Zhen,Li Ting,et al. System design and analysis for improving geometric accuracy of high-resolution optical remote sensing satellite image [J]. Journal of Astronautics,2013,34(8): 1159-1165 (in Chinese)

[6]王仁享，王建荣，胡莘.卫星摄影姿态测定系统低频误差补偿[J].测绘学报，2016,45(2):127-130

Wang Renxiang,Wang Jianrong,Hu Xin. Low-frequency errors compensation of attitude determination system in satellite photogrammetry [J]．Acta Geodaetica et Cartographica Sinica,2016,45(2): 127-130 (in Chinese)

[7]王任享. 三线阵CCD 影像卫星摄影测量原理[M]．北京：测绘出版社，2006:1-60

Wang Renxiang. Satellite photogrammetric principle for three-line-array CCD imagery[M]. Beijing: Surveying and Mapping Press,2006:1-60 (in Chinese)

[8]智喜洋，张伟，曹移明,等，单线阵CCD 相机定位精度评估模型及几何误差研究[J].光学技术，2011，37(6)：669-674

Zhi Xiyang,Zhang Wei,Cao Yiming,et al. Study on positioning accuracy assessment model and geometric errors for single-linear-array CCD camera[J]. Optical Technique. 2011,37(6): 669-674 (in Chinese)

[9]蒋永华，张过，唐新明，等. 资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报，2013，42(4)：523-529

Jiang Yonghua,Zhang Guo,Tang Xinming，et al.High accuracy geometric calibration of ZY-3 three-line image[J]. Acta Geodaetica et Cartographica Sinica,2013，42(4)：523-529 (in Chinese)

[10]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉：武汉大学出版社，2003

Surveying Adjustment Discipline Groups of Surveying and Mapping School of Wuhan University. Theory and measurement error adjustment[M].Wuhan:Wuhan University Press,2003(in Chinese)

[11]Gruen A，Zhang L. 3D Processing of high-resolution satellite images[C]// Busan，Asian Conference on Remote Sensing 2003. Korea：ACRS,2003:390-394

(编辑：李多)

Discussion of Geo-location Accuracy Increasing Methods of Agile Satellite Without Ground Control Points

LI Zhen JIN Tao LI Ting YANG Dong

(Beijing Institute of Spacecraft System Engineering,Beijing 100094,China)

In light of geo-location accuracy of the agile optical satellite,this paper proposes a fine locating propagation model which distinguishes the high-frequency and low-frequency attitude errors,as well as considering the system design parameters. By the simulation analysis,the influence law of the low-frequency error and attitude stability error to the final location accuracy is presented. Taking the 30m location accuracy and the map scale of 1∶50 000 as an example,the value of index is analyzed and the methods of increasing geo-location accuracy is put forward. The result is that the low-frequency errors mainly impact the horizontal geo-location accuracy. The 30m accuracy would be met with no more control to the attitude problem,but only imaging with larger and symmetric intersection angles. If the satellite attitude measurement accuracy reaches 0.9″and the 200 Hz high-frequency attitude measurement equipment and the on-orbit angle measurement equipment are used between the star track and the camera,also with the control of the low-frequency errors within 5″,the accuracy for the map scale of 1∶50 000 (plan 15m and height 6m) would be met.

agile optical satellite; without ground control points; locating accuracy; low-frequency errors; attitude interpolation; attitude stability

2016-09-22；

2016-11-08

国家重大航天工程

李贞，女，硕士，工程师，从事航天器有效载荷总体设计、光学遥感卫星几何定位精度总体设计等研究工作。Email：schnappilee@foxmail.com。

P236

A

10.3969/j.issn.1673-8748.2016.06.005