关注考纲变化，赏析数学文化

李晨硕

2017年普通高考考试大纲将特别提出将数学文化渗透到高考命题中，数学文化怎样在高考试题中体现，大概有这几种方式：涉及数学史、涉及数学名题、渗透数学美、涉及数学应用、涉及数学语言，下面列举一些渗透数学文化的题目，为复习备考指路。

例1：（2011年湖北理科）《九章算术》“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则第5节的容积为                              .

赏析：本题借用《九章算术》“竹九节”问题来考查等差数列的通项公式和数列的前项和公式，先求出首项和公差，然后再由等差数列的通项公式求第5节的容积。本来非常简单的等差数列问题，在数学史的衬托之下精彩无限。这将引领师生在数学教与学活动中更多地关注数学文化元素。

例2：（2013湖北理科）我国古代数学名著《数书九章》中有“天池盆测雨”题：在下雨时，用一个圆台形的天池盆接雨水，天池盆盆口直径为二尺八寸，盆底直径为一尺二寸，盆深一尺八寸，若盆中积水深九寸，则平地降雨量是                   寸（注：①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸）

赏析：历史上，中国数学取得了辉煌的成就，出现过众多的数学名著，《数书九章》概括了宋元时期汉族传统数学的主要成就，是对《九章算术》的继承和发展，引入古代数学名题，既符合学生认知水平，又可以引导学生关注中国传统文化。

例3：（2015年全国卷I）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺。问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有（  ）

赏析：该问题源于生活中粮食储存，与立体几何体积求解的基础知识相结合，可以让学生体会到古代数学的优秀传统——数学要关注生产、生活等社会问题，引导学生了解数学文化，体会数学知识在认识世界中的工具作用。体现了数学文化“以数化人”的功能。

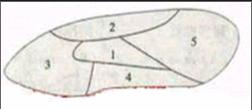
例4：（ 2003年全国卷） 如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有种.（以数字作答）

赏析：这是涉及四色定理的问题，是世界三大数学猜想之一。四色定理的本质许多人认为是在平面或者球面无法构造五个或者五个以上两两相连的区域。其本质在与地图上是否可以只用四种颜色着色，从而演变出一个几何上的数学问题，

例5： （2014湖北，理）设a是一个各位数字都不是0且没有重复数字的三位数，将组成a的3个数字按从小到大排成的三位数记为I（a），按从大到小排成的三位数记为D（a）（例如a=815，则I（a）=158，D（a）=851）.阅读如图所示的程序框图，运行相应的程序，任意输入一个a，输出的结果b=                          .

赏析：题目中的“更相减损术”是解决“求两个数的最大公约数”问题，外国的欧几里德算法也可以解决这个问题，但是我国的发现比外国的算法更简单，操作起来更方便，更符合算法的要求。这样设计，不仅可以让学生理解数学文化，形成理性思维，同时也能学生感受我国古代数学的成就，增强爱国情怀。