基于离散元法的沥青混合料抗剪切性能初探*

李 明 姜德乾

(山东科技大学 山东省土木工程防灾减灾重点实验室，山东 青岛 266590)



基于离散元法的沥青混合料抗剪切性能初探*

李 明 姜德乾

(山东科技大学 山东省土木工程防灾减灾重点实验室，山东 青岛 266590)

运用二维颗粒流程序PFC2D，建立单轴贯入试验模型，通过模拟加载试验，从细观角度分析沥青混合料中颗粒的运动位移和颗粒间接触力随着贯入量的增加所产生的变化，探究确定微观参数的方法，得到模拟试验的应力-应变曲线和真实的单轴贯入试验数据，为后续模拟提供借鉴。

离散元法；单轴贯入试验；微观参数；抗剪切性能

沥青路面以其良好的路用性能而得到广泛应用，但是在高温和行车荷载的作用下，路面会出现车辙病害，该病害的发生也引起了相关技术人员的关注，通过车辙试验来测量不同种沥青混合料的动稳定度是判断沥青混合料抗车辙性能比较常见的方法。毕玉峰等[1]在以前试验的基础上提出用单轴贯入试验来分析沥青混合料的抗剪切性能，该试验操作简单而且与实际相关性较好。

近年来随着各种商业软件的开发和技术的延伸，许多学者开始运用离散元软件研究沥青混合料的性质，胡霞光[2]分析了沥青混合料基于现象学的经验方法的弊端，总结了离散元方法的优点，王端宜等[3]模拟了沥青混合料单轴压缩试验，发现了试件细观结构和宏观本构行为之间的联系，陈俊等[4]运用离散元法模拟了沥青混合料小梁疲劳试验，得到了细观破坏机理，郭红兵等[5]对比不同马歇尔试件的劈裂试验，得出各试件抗裂性能差异，张德育等[6]模拟了车辙试验，得出了沥青混合料中粗集料的空间运动状态。本文运用基于离散元理论的分析软件PFC2D，模拟沥青混合料单轴贯入试验，从细观角度[7-8]分析沥青混合料抗剪切性能。

1 离散元理论

离散元方法研究的是有离散特性的物质[9]，离散单元可以出现变形不连续状态，因此不需要满足变形协调方程。离散元法只需满足物理方程和运动方程即可。

1.1 物理方程

物理方程即力—位移关系方程，离散元法中颗粒间接触力和颗粒间接触重叠区域的大小存在线性关系，以颗粒接触刚度作为该线性方程比例系数。

Fn=KnUn

式中：Fn为法向接触力，Kn为法向接触刚度，Un为法向重叠量。

1.2 运动方程

运动方程即牛顿第二定律，通过物理方程可得到接触力，代入运动方程得到加速度，之后通过有限中心差分法得到的速度、位移等，通过动态松弛迭代即可得到任意时刻的速度、位移。

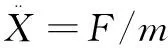
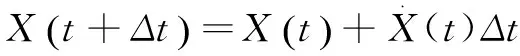
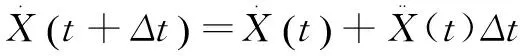
θ(t+Δt)=θ(t)+ω(t+Δt/2)Δt

2 单轴贯入试验

以直径与沥青试件相比足够小的圆柱形钢压头模拟车轮荷载，施加在尺寸为Φ100mm×100mm的圆柱型沥青试件的上表面中央处，沥青试件相当于路面结构，钢压头保持1mm/min的速度匀速下降，记录加载过程中压头的作用力和沥青试件的竖向变形，直至试件破坏为止。试验模型如图1所示。

图1 单轴贯入试验模型

2.1 原材料选择

沥青混合料是由粗集料、细集料、矿粉、沥青胶结料按照一定顺序和比例添加拌和而成，原材料的性质直接影响混合料的路用性能，因此应该选择符合规范要求的原材料。粗集料应当干燥、洁净、表面粗糙；细集料应当洁净、干燥、无风化、无杂质，并有适当的颗粒级配；矿粉必须是从石灰岩或岩浆岩中的强基性岩石等憎水性石料磨细得到，应满足洁净、干燥，可从矿料仓自由流出的要求。本试验选择的集料是产自青岛平度灰埠，沥青选择A-70基质沥青，集料级配应符合规范要求[10]，本试验所选沥青混合料为AC-13，空隙率n=4.3%，集料级配曲线如图2所示。

2.2 试验模拟过程

运用离散元软件PFC2D中自带的FISH语言程序，编写代码，生成与合成级配相同的沥青试件，PFC2D中颗粒生成必须限定在一定范围之内，因此颗粒生成之前应建立封闭集合区域，使得颗粒在封闭区域的有效面内生成，本试验模拟的沥青试件为圆柱体，因此首先应按照逆时针方向生成4面墙体围成100mm×100mm的矩形区域。由于本试验是在无侧限支撑情况下进行的，因此在建立模型之后应去除两侧墙体，已达到模拟的真实性。所建离散元模型如图3所示。

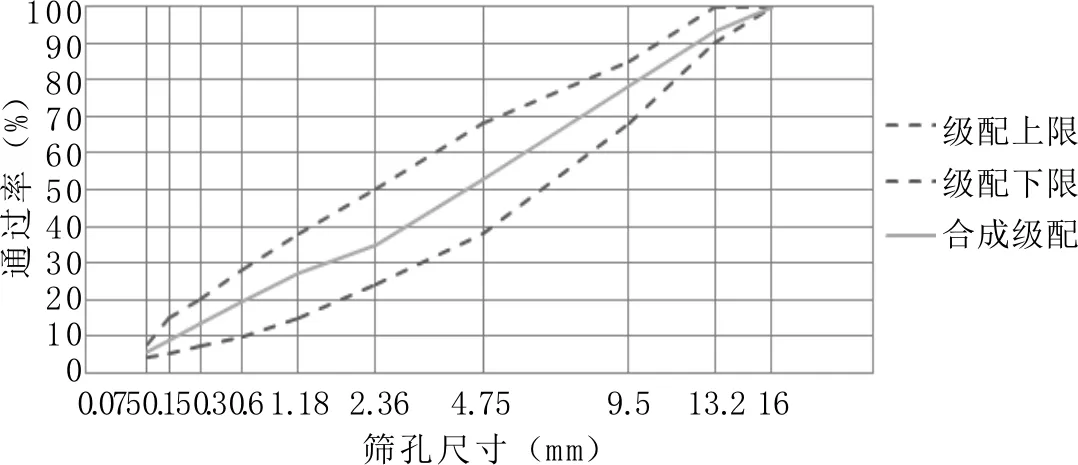
图2 AC-13级配曲线

图3 离散元模型

试验加载前应先去掉顶面墙体，按照压头的尺寸和位置，再在顶面的适当位置建立一面墙体来模拟压头，通过墙体的移动来模拟加载过程。沥青混合料宏观属性的模拟，需借助离散元软件提供的颗粒接触模型来实现。离散元法中提供了刚度模型、滑移模型、粘结模型，其中粘结模型又包括接触粘结模型与平行粘结模型，沥青混合料是一种把粗细集料通过沥青胶结料粘结而成的材料，该材料具有承受力和力矩的性能，与平行粘结模型的特征比较接近，因此选择该接触模型进行模拟。

模型微观参数的选取直接影响模拟结果和试验结果的吻合程度，但是就现阶段而言，参数的选择一直是个难题，最准确有效的方法是先根据已有经验选取一组微观参数，通过试验和模拟结果对比，如果出现差异可继续调节，直至两者吻合度较高时，确定试验微观参数，调节过程如图4所示，所选参数见表1。

表1 建模微观参数

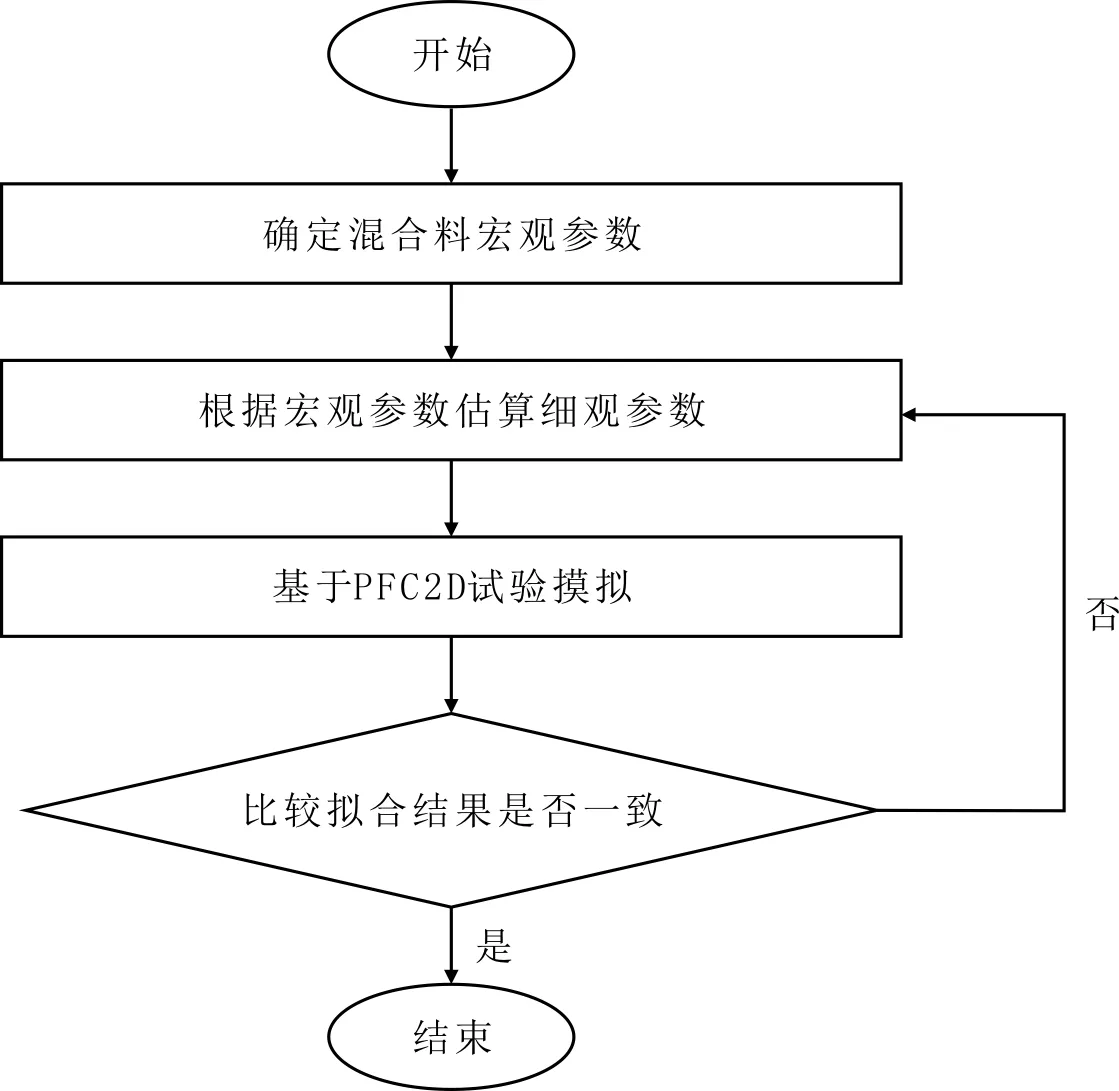
图4 参数调试过程

2.3 试验结果分析

加载过程中试件接触力变化如图5所示，可看出加载面部位接触力相对密集，随着加载时间的变化，贯入量也随之增加，同时接触力也随贯入量的增加而向竖直方向延伸，加载中期以后接触力向下扩展趋势减小，试件两侧明显隆起，说明沥青面层其主要抗剪切作用的是中上部，随着深度的增加，抗剪切性能先增后减。

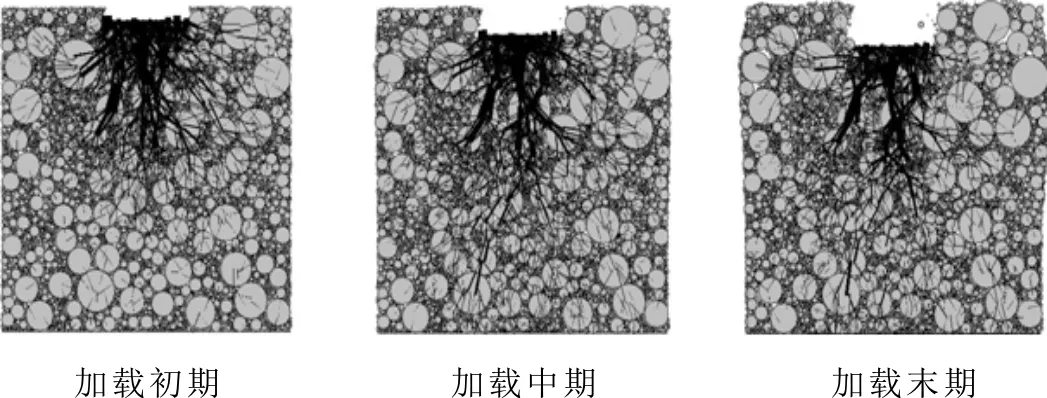
图5 加载过程接触力图

接触力的传递特征是以粒径较大颗粒作为中心向四周颗粒传递，因此适当增加混合料中粗颗粒数量也有助于增强其抗剪切性能。

离散元软件PFC2D可根据需要，得到任意颗粒单元在任何时刻的位移和速度等信息，为研究颗粒的运动特征，选择在加载面附近的颗粒编号id=42的颗粒(该颗粒具体位置已在图3中标明)，监测加载过程中此颗粒的位移矢量和速度矢量信息，如图6、图7所示。

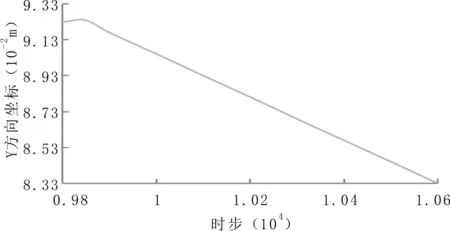
图6 Y轴方向位移矢量信息

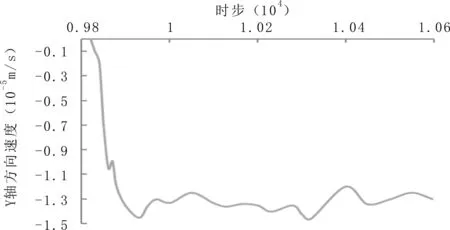
图7 Y轴方向速度矢量信息

由图6可知，在接触面附近的颗粒在Y轴方向的运动状态基本与加载板的加载速度成正比，位移呈线性变化，由图7可知，颗粒在Y轴方向刚开始时速度变化率很大，加载速度呈现先逐渐增大，之后基本保持不变。

实际单轴贯入试验和模拟试验的应力-应变曲线如图8所示，通过微观参数的调节后，两者差别不大，AC-13沥青混合料试件的最大轴向应力约为1.35MPa，对应轴向应变为0.05。

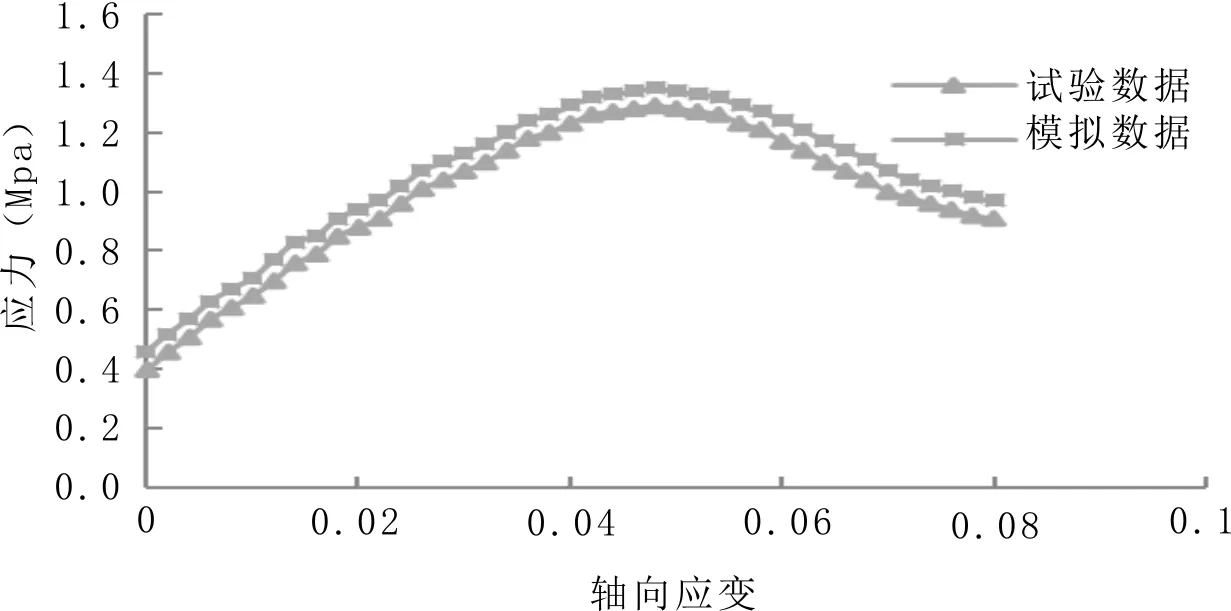
图8 应力-应变曲线

3 结论

(1)随着贯入量的增加，颗粒间接触力也向下传递扩展，加载中期至末期，接触力向下传递趋势减小，说明沥青层的抗剪切性能主要取决于层厚的中上部，并非层厚越厚，抗剪切性能越好。

(2)离散元法可监测组成沥青混合料试件任意单元的运动状态，这为细观分析提供了便利。通过微观参数的调试，试验结果和模拟结果基本一致，因此抗剪强度可直接通过模拟得到。

(3)要想使模拟结果与实际试验结果更加接近，在今后模拟中还应考虑集料的棱角性对试验结果的影响。

[1]毕玉峰,孙立军.沥青混合料抗剪试验方法研究[J]. 同济大学学报(自然科学版)，2005，33(8):1036-1040.

[2]胡霞光.沥青混合料微观力学分析综述[J]. 长安大学学报(自然科学版)，2005，25(2):6-10.

[3]王端宜,赵熙.沥青混合料单轴压缩试验的离散元仿真[J]. 华南理工大学学报(自然科学版)，2009，37(7):37-40.

[4]陈俊,黄晓明.基于离散元法的沥青混合料虚拟疲劳试验方法[J]. 吉林大学学报(工学版)，2010，40(2):435-440.

[5]郭红兵，陈拴发.开级配大粒径沥青碎石混合料劈裂试验的离散元数值分析[J]. 公路交通科技，2014，31(11):22-26.

[6]张德育,白桃,黄晓明,等.沥青混合料永久变形过程中粗集料空间运动分析[J]. 建筑材料学报，2015，18(3):421-427.

[7]陈渊召,李振霞.基于离散元法的橡胶颗粒沥青混合料细观结构分析[J]. 哈尔滨工业大学学报，2013，45(4):116-121.

[8]郭红兵,陈拴发.设置OLSM-25防裂层的沥青路面细观结构数值分析[J]. 长安大学学报(自然科学版)，2015，35(3):34-39.

[9]Itasca Consulting Group.Particle flow code in two dimensions (PFC2D) Manual Version 3.1[M].Minneapolis: Itasca Consulting Group,2003.

[10]交通运输部公路科学研究院.公路工程集料试验规程(JTG E42-2005)[S]. 北京：人民交通出版社，2005.

2016-11-10

山东省自然科学基金“城区低维护复合式基层沥青路面结构应用研究”(编号：ZR2011EEQ027)。

李 明(1987-)，男，山东日照人，山东科技大学硕士研究生，主要从事路面结构和材料研究。姜德乾(1989-)，男，山东青岛人，山东科技大学硕士研究生，主要从事结构设计理论与应用研究。

10.3969/j.issn.1672-9846.2016.04.018

U414

A

1672-9846(2016)04-0073-04