约束与选择:二胎均衡及其政策意义
王晓瑞
(北京社会管理职业学院 信息中心,北京 101601)
约束与选择:二胎均衡及其政策意义
王晓瑞
(北京社会管理职业学院 信息中心,北京 101601)
运用博弈理论分析了中国农村计划生育过程中两胎均衡的形成。首先对比了韦伯社会行动的概念与互动博弈的概念,然后介绍了几个与博弈理论相关的概念:重复博弈、信息与理性预期。在此基础上,以博弈理论的思想为基础,以实证调研数据为支撑,建立并分析了二胎均衡模型。二胎均衡模型在实践层面主要涉及中国目前的养老问题和性别比失调问题,分析了模型对于老年社会福利政策的制定和消减性别比例等方面的意义。
互动博弈;二胎均衡;理性预期
我国计划生育政策已经实施30多年,30多年计划生育政策的影响不言而喻。据国家统计局第六次全国人口普查的数据显示,与2000年第五次全国人口普查数据相比,全国总人口增加了1.3亿,年均增长0.57%,0—14岁人口的比重下降了6.29个百分点,15—59岁人口的比重上升3.36个百分点,60岁及60以上人口的比重上升2.93个百分点[1],由此可见,10年来我国人口增长长期处于低生育水平。人口生育长期低水平发展会有什么影响?实际情况是什么样?本文从社会行动与博弈论的角度出发,以一个乡村二胎均衡的形成为案例,来分析目前计划生育中的运作逻辑和后果,期待对有关改革实践有所裨益。
1 社会行动、互动博弈与理性预期
有经济学家认为,经济学是研究人们如何做选择的学科。而社会学家则认为,人们的选择是在社会的约束条件下做出的,比如戈兰诺维特[2]就认为,人们的经济行为是嵌入在社会结构和关系之中的。笔者认为,社会学家更多地强调个人选择的局限条件,比如社会结构、制度规范等,而经济学家更多地关注选择本身,把约束条件给定。实际上两门学科都承认人们在做选择,并且选择有约束条件,在这两点上两个学科是有着沟通的基础的。经济学帝国主义的形成是有着它内在的逻辑的,因为在它的理性人前提下做利益最大化选择的假设和它对人类行为的解释力,确实有着无可置疑的优势。用福山的话来说,就是经济学可以解释人们行为的80%。那么融合社会学和经济学的优势,来解释人们的行为,将会获得更好的效果,更逼近真实世界,经济学也可以远离“黑板经济学”的坏名声。博弈论无疑可以成为二者沟通的桥梁。
博弈论主要是研究人们的策略互动行为的理论。在社会学意义上,值得社会学家注意的是,博弈是特殊的社会行动,强调互动,要考虑到他者的行为和意图来做出选择,这正符合韦伯[3]的社会行动概念。之所以说行动是社会的,是因为,根据行动的个人附加在行动上的主观意义,行动必须把他人的行为考虑进去,并以此确定行为取向。社会行动,包括不能行动和被动默许,都指向他人过去的、现在的或者预期的、未来的行为。博弈论正是这种互动的策略行为,只是前提假设是人们的行为是理性的,在局限条件下做出最符合自己利益的选择。因此可以说,博弈行为是特殊的一类社会行动。对这一类行动的研究,就可以借用理性选择来分析社会行为。那么什么是博弈论?一般而言,博弈论是对人们在策略互动中是如何行为的研究。谢林[4]认为,“博弈论是对诸种情境中的理性选择的研究。两个人或者多个人,有选择要做,有关于后果的偏好,知道一些相互可以获得的选择以及相互的偏好。”因此,对一个问题的解决,都是对双(多)方参与者而言的。任何一方必须学会从对(他)方考虑问题,找出解决方法,实现自己的利益最大化,也就是学会在局限条件下做出理性的选择。此外博弈必须考虑时间因素。艾克斯罗德[5]就认为,时间因素对博弈最后形成合作很重要。另外基德兰德和普雷斯科特[6]的经典著作指出,由于时间一致性问题,制定规则比相机抉择对社会目标函数结果更优。奥曼[7]在进行博弈论分析的时候,研究的是不完全信息的重复博弈,就是在这种重复博弈中,双方都在向对方暴露着自己的信息。最重要的是每方都要知道对方是如何评估形势或情境的,这样就会在下一轮的博弈中调整自己的策略。
2 计划生育中的互动博弈和二胎均衡模型 ̄
笔者利用陈村2000年底和2001年的调查资料来建立模型和进行分析[8]。调查和统计发现,经过20多年的计划生育博弈,出现了渐趋稳定的二胎均衡的“弹性动态平衡”,即每对夫妇生育子女数量基本上保持在两个或3个,而以两个的居多,且绝大多数都是一男一女,约占85%。弹性的两端,一端是村民的生育意愿或偏好,另一端是控制人口的国策及其执行。
这里,博弈背景即计划生育的“一对夫妇只生一个孩子”政策是大前提,当然二女户、小孩有缺陷等情况,政策另有规定。政策的执行者——当地的行政管理人员,分编内和编外,我们统称为管理执行方,我们把他们假定为博弈的一方。另一方是陈村村民。作为一个普通村庄,村民的生育观念近几十年没有明显改变,养儿防老、传宗接代的观念依然很重要。所以突破一胎化政策,要有儿有女,尤其要有传宗接代的男孩子,就成为博弈另一方的选择。管理执行方的偏好是,完成上级下达的任务,实现一胎化的计划生育政策,把这个任务的完成,归为一项收益a;但是,假定村民的偏好也是这样,只生一个孩,收益为b,那么,双方都没有要克服什么困难的成本,因此在这个意义上,定义双方的成本都是0。这样就构成了下面表1中的A(a,b)。假定政策偏好是二胎化,无条件允许二胎,而村民的生育偏好是一胎。那么,双方都同样获得自己的收益,依然是a和b,也就是表1中的C(a,b)。
但是,村民的偏好不是一胎化,而是两个或者更多个孩子。对于管理执行方,也不是只图完成政策任务,而要在这个过程中收到计划生育罚款,因为完成任务只是对少数有升迁前途的人员或者保住自己原有职位的人员才有意义。那些编外人员没有这个期望,他们就想在这中间获益。他们付出了很大的辛苦,甚至冒着获得不良名声的危险来干这项工作。而且,乡财政还要给他们派任务,要上缴一定的罚款,甚至或明或暗地分派给每个人一定的上交罚款任务,完不成,要么受批评,要么下岗。这样一来,表1的A是不可能实现的情况。假定管理执行方严格控制在一胎化,那么受到村民的抵抗力就极大,从而就要付出成本c,即使实现了一胎化,完成了任务,收益也就是a-c;同时对村民来说,抵抗严格的政策要付出一个代价,假定为c,等于执行方的代价,而且因为没有实现自己的生育还要减去一个损失d,村民的收益就构成了表1中的B(a-c,b-c-d)。假定在国家一胎化政策下,管理执行人员做点变通,也就是不是实现一胎化,而是允许生育二胎,那么就可以通过罚款来惩罚超生村民。这样,村民接受罚款,比严格的一胎化较容易接受;而管理执行人员,也可以少些阻力,还可以获得罚款的收益。实际上,相关法规是有超生罚款条款的,管理执行人员这么做也不算违法。村民如果太过分,比如超生过多,四五个孩子,那样,上级政府就不可能容许,所以一般就选择二胎。结果是,管理执行方因为无法实现完美的“模范”目标“一胎化”而失去一个代价e,但是e远远小于c,同时获得了一个可观的罚金f;而村民失去了金钱m,但是突破了一胎化,实现了两个孩子的偏好,获得了一个d(d>m)。这样就形成了一个真正的最优博弈均衡D(a-e+f,b-m+d),即二胎均衡,个别特殊情况超过二胎,详见表1。

表1 博弈矩阵
把管理执行人员一方的付出和收益关系用图2来表示。付出,即代价,经济学用语为成本,用C来表示。毛收益也就是没有扣除成本之前的收益,用G表示。图2中有两条线,一条是表示毛收益和成本之间的关系,其函数关系是G=F(C)。另一条是毛收益和成本等同线G=C。净收益P=F(C)-C。当付出不能够达到一定程度时(0≤C 图2 管理执行人员的付出和收益关系 这个均衡点不是一开始就明确的,而是在博弈过程中形成的。陈村计划生育二胎均衡这个结果是20世纪90年代末和21世纪初的实际现状和趋势,也是陈村村民与执行管理人员在20来年无数次重复博弈基础上形成的。刚开始,管理执行人员对于将会遇到的困难也不是很清楚。村民面对管理人员也不知道对方会严格到何种程度。20世纪80年代初不是很严格,后来上级领导不满意,严了一阵子。陈村自1979年开始计划生育,到1985年7年间,出生三胎5人,四胎和五胎没有,六胎1人。乡村在改革开放中以经济建设为中心后,计生政策的执行又开始放松,从1986年开始超生现象猛增,超生人数相应地增长,到1989年达到高峰,1989年,陈村共超生了10人;之后,计生政策执行转向严格,成了领导干部政绩的主要一项内容,计划生育工作有一票否决权;到1993年左右,就出现了掀瓦扒房、抓人流产、亲邻受牵连等行为。20世纪80年代的乡村,腐败没有多少资源,但是,随着村民致富,村民贿赂管理执行人员的行为越来越多,数额越来越大。以计划生育罚款的名义,到超生户(及其亲邻)家拿走东西作为罚款的问题也越发严重起来。太严格和太松的尝试都经过之后,双方都有了经验和教训,知道了对方的偏好和可接受的范围。后来,有些村民迫于早期的惊恐现象,不敢超生,计生人员还会去动员生二胎。都在一胎范围,就不会有罚款收益。就是上面图2中C的情况。基于这样的情况,出现了二胎均衡。但这个均衡是动态的,不是完全严格意义上的二胎形成;特殊情况下,也会出现二胎以上孩子的超生。 在这个过程中,合作和冲突都共同存在着作为“阳”的合作和作为“阴”的冲突,在消长中不断地调整着,达到一种阴阳的平衡。这种阴阳的调和需要一种心照不宣,也就是静默的沟通。为什么在冲突的博弈中,还会存在心照不宣的交流?因为是混合动机冲突的存在,导致了收支盈利的多面性。在这个过程中,两者就合作起来,一起欺瞒上级政府。比如上级来检查计划生育执行情况,乡镇政府计生所上报一本假账,同时及时通知村民,把超生的“小黑孩”藏起来,瞒过检查人员。这就是两者合作的一面。正是有阴的一面,也要有阳的一面。艾克斯罗德在研究合作的进化[5]中指出,“自己活也让别人活”使得在敌对双方之间都可以达成合作。考虑到要有足够的时间达成默契合作,那么,在这样的乡土社会、熟人社会里,这种默契更易达成。 从陈村的情况看到,如果真正按照一胎制的政策坚决执行,从博弈模型中可以看出,对双方都不利。但通过实践中的不断调整,使得管理人员一定程度上完成了任务,同时也获得了金钱收益。而村民也得以突破一胎制,实现二胎,或者更多孩子。这样一定程度上也缓解了农村老龄化社会问题和社会保障问题。这就是收益和代价并存的情形。对于村民来说,这种代价是值得的。对于社会和决策人来说,也是能够理解且对社会有益的。而且虽然陈村村民被排除在政策制定参与者之外,他们所做的只是被动的“兵来将挡,水来土屯”,但相对城市居民被国家控制着“铁饭碗”资源的劣势,农村村民有了更大的生育空间和生育的可能性。 这样,陈村两胎均衡就有了它的逻辑意义。两个孩子在概率上说,有4种情况:男、女;女、男;男、男;女、女。这样,在统计学的概率意义上,一对夫妇至少生一个男孩的概率为75%,理论上会有25%的夫妇没有男孩子,因而不满意。如果只让生一个孩子,村民得到男孩的概率是50%。那么,会有50%的夫妇不满意。事实上,对陈村的调查表明,两个子女的夫妇近90%都是一子一女。个别的头两胎是女孩的夫妇如果可能生第三个孩子的话,那么整体而言,一对夫妇至少有一个男孩的概率将会更接近100%(87.5%)。这样,就可以缓和村民与计划生育政策执行者的矛盾。对村民来说,动态的二胎平衡是可以接受的。 当然,陈村情况是一种特殊情况下的博弈,如果在占人口36%的地区严格实行一胎制度,即使在占人口一半以上地区实行一孩半政策,受传统重男轻女和男孩传宗接代观念的影响,村民更希望男孩优先。由此很多地方有可能通过人为的方式,在第二胎,运用高科技比如B超鉴定出胎儿性别,在婴儿出生之前就做出性别选择;出生后,溺女婴弃女婴现象也出现过。这样导致的结果就不是谢林理论上所预测的男女比例为1:1的结果;而在占人口一半以上地区实行的一孩半政策,其结果也将直接导致男女比例严重失调。2007年大陆男女出生性别比为1.20∶1就是明证。由上面关于一对夫妇生两个孩子可以获得至少一个儿子的概率的分析中知道这个概率是75%,比一胎是男孩的概率高出25%,这样就减少了很大的政策执行压力。再考虑到上面所讨论的农村实际的养老问题,二胎的收益更大。因此二胎化比一胎化的优势是明显的。20世纪80年代,山西翼城作为首个人口特区所做的二胎化试验,实行的是晚婚晚育加间隔的形式。其试验结果:该县各项人口指标数据均优于全国,人口增长量低于全国平均水平,男女性别比为1.06∶1。而有学者,如曾毅曾撰文指出,如果二胎晚育软着陆后,中国目前的这种生育性别比在2030年左右恢复正常[9]。放开二胎后对出生性别比的影响,在考虑人为因素的情况下,陈村的二胎均衡具有一定的启发。 此外,老龄化社会的来临越来越为社会所关注。我国实施的计划生育政策,尤其是独生子女政策的实施,使得“独一代”享受了父母爷爷奶奶外公外婆6个“爱”,集“六爱”于一身,被称为“小太阳”。但是他们成人后面临的则是向“六爱”的回报。现在城市人口有养老保障金问题,农村人口的养老保障金也在试点进行中,但就老年人的生活照顾而言,指望这个“小太阳”,恐怕不太可能。有学者指出,在中国度过了30年的人口红利期后,人口的生育率如果一直在低水平徘徊,将会现现“人口负担”,人口“赡养系数”的提高将给中国经济发展和老龄化养老问题带来大的负面影响。其中所涉及的不仅仅是钱的问题,也是社会心理支持的问题、生活照顾的问题,终究是社会和经济的问题,也是政治稳定的问题。但也有学者指出,目前国内外有很多学者存在对中国人口红利消失和老龄化危机认识上的误导现象[10],因为我国现在面临的不是劳动力短缺的问题,而是剩余劳动力长期存在的问题。对计划生育政策方面微小的调整倒也可以,但如果全面放开,则会因小失大,丧失掉我国几十年来在计划生育方面所做的努力,是不负责的做法。用后一种观点来看,如果用剩余劳动力的角度来看待人口赡养系数的话,那么未来老年人的养老模式将不再是以家庭为主的养老模式,而是以机构养老或者社区养老为主,那么这样对我国目前的养老文化和养老制度来讲,将是一个巨大的挑战。在看待二胎均衡问题上,走什么样的路线,怎么样放开二胎,将涉及方方面面的事情,还需要不断试验总结。 计生政策的调整不可能一蹴而就,它有一个动态博弈的过程。目前,有专家和官员对二胎问题已经做过调查和研究,“十二五”末期,二胎政策是否放开也被放进了议事日程,中间将会出现一个博弈的过程。只有在博弈的互动过程中,才能有更多的信息被暴露出来,然后做出政策调整,这样才能更符合实际情况。在政策制定过程中,要充分考虑村民的生育意愿,因为生育意愿反映的更多的是生育私权,当然,这个私权是社会经济发展水平生育公权影响下的一种私权,博弈双方都必须考虑实际可行性,而不只是一方意愿。以上分析也显示了博弈过程的复杂性,对政策的后果也很不容易精确地预测。人的有限理性[11]和复杂的现实因素导致有时候行动的后果和预期并不一致,会出现吉登斯[12]所说的“控制辩证法”带来的“意外后果”。研究这种现象的趋势和功能,目的就是要增强认识,调整政策,也就是调整博弈的规则,以求其朝向社会整体发挥正功能的方向发展。 [1] 国务院人口普查办公室,国家统计局人口和就业统计司.中国2010年人口普查资料[EB/OL](2016-10-02).http://www.stats.gov.cn/tjsj/pcsj/rkpc/6rp/indexch.htm.[2] GRANOVETTER M. Economic action and social structure: A theory of embeddedness[J].American journal of sociology, 1985(91): 481-510. [3] WEBER M. Basic concepts in sociology[M]. New York: Philosophical library ,1962. [4] SCHELLING, THOMAS C. Choice and consequence[M]. Cambridge MA: Harvard university press ,1984. [5] 罗伯特﹒艾克斯罗德.对策中的制胜之道[M].吴坚忠,译.上海:上海人民出版社,1996. [6] KYDLAND F E, PRESCOTT E C. Rules rather than discretion: The inconsistency of optimal plans[J].Journal of political economy, 1977( 85): 473-492. [7] AUMANN, ROBERT J. Repeated games with incomplete information[M].Cambridge MA: MIT press, 1995. [8] 陈心想.从陈村计划生育中的博弈看基层社会运作[J].社会学研究,2004(3):93-102. [9] 曾毅.二孩晚育软着陆方案有利于解决我国出生性别比偏高问题[J].社会科学,2009(8) :54-188. [10] 侯东民.国内外思潮对中国人口红利消失及老龄化危机的误导[J].人口研究,2011(3):29-40. [11] 西蒙.现代决策理论的基石[M].杨砾,徐立,译.北京:北京经济学院出版社,1989. CONSTRAINT AND CHOICE: EQUILIBRIUM OF A SECOND CHILD AND ITS POLICY IMPLICATIONS WANG Xiaorui (InformationCenter,BeijingSocialAdministrationVocationalCollege,Beijing101601,China) The paper uses game theory to analyze the forming of two-children-equilibrium in the process of China's rural family planning. First of all, the author compares Weber's concept of social action and the concept of interactive game, and then introduces several concepts related to game theory: repeated game, information and rational expectations. According to this, the paper establishes and analyzes a second-child-equilibrium model based on game theory and supported by empirical research data. The enlightenment of the second-child-equilibrium model to population problem at the practical level mainly involves the current pension problem and gender ratio imbalance. The paper analyzes the significance of the model to the development of social welfare policy for the elderly and the reduction of gender ratio. interactive game; a second-child-equilibrium; rational expectation 2016-10-09 王晓瑞(1976-),女,河南许昌人,硕士,讲师,研究方向:社会学、社会工作。 1673-1751(2016)04-0061-05 C923 A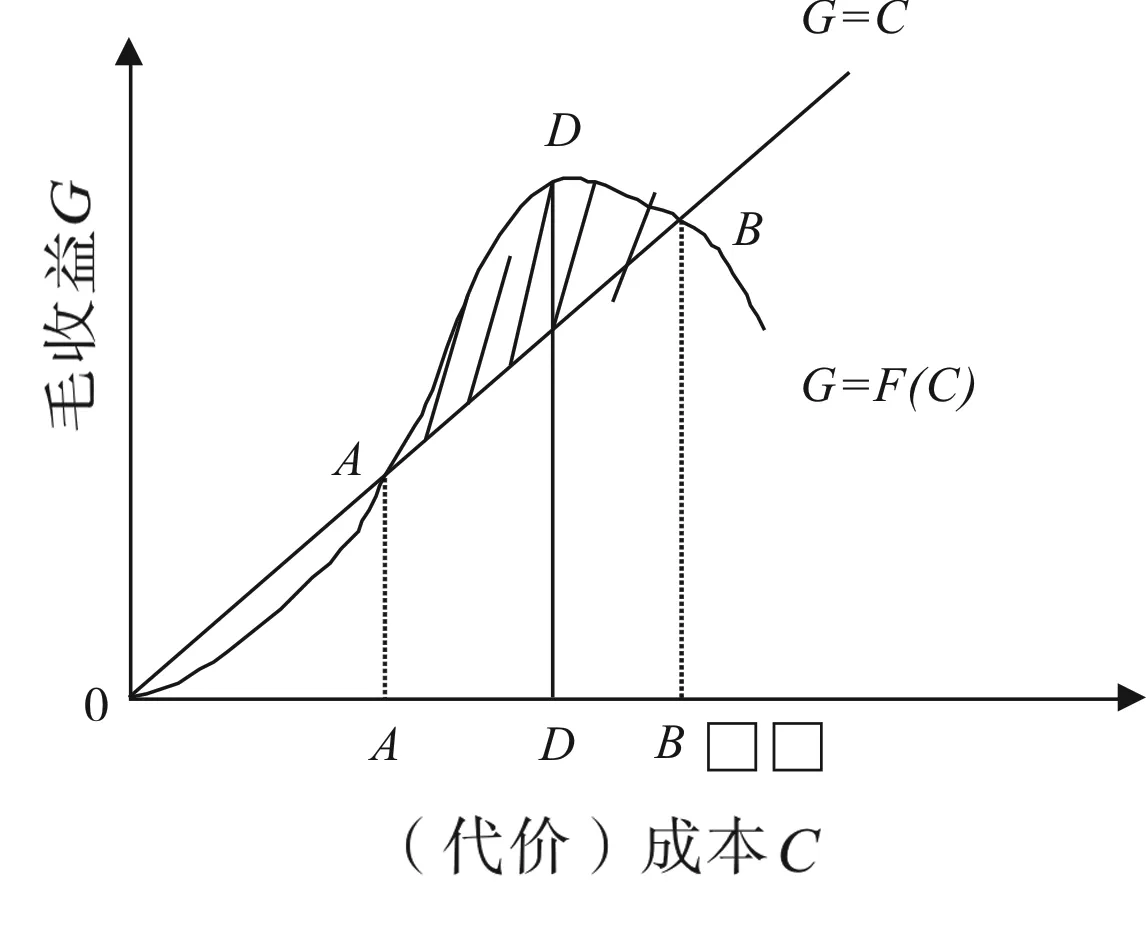
3 二胎均衡的可能性及对老龄化和性别比例的影响

