单、双层主动吸声材料驱动电压的计算

朱从云， 朱继华， 朱永智, 黄其柏

(1.中原工学院, 郑州 450007; 2.河南森源重工有限公司, 河南 长葛 461500；3.华中科技大学 机械科学与工程学院， 武汉 430074)

单、双层主动吸声材料驱动电压的计算

朱从云1， 朱继华1， 朱永智2, 黄其柏3

(1.中原工学院, 郑州 450007; 2.河南森源重工有限公司, 河南 长葛 461500；3.华中科技大学 机械科学与工程学院， 武汉 430074)

介绍了单、双层主动吸声压电材料表面驱动电压的计算方法：单层主动吸声系统以一层压电材料作为驱动电压来防止反射波的传播，双层主动吸声系统则通过两层压电材料的协调来防止反射波和投射波的传播。分别通过理论法和声电类比法对单层主动吸声系统和双层主动吸声系统两种方式进行计算、比较和分析。其中，理论法根据相关定理和定律对主动吸声方式进行解释，声电类比法则将产生的声信号与电或力的情形相类比。采用Matlab软件对以上两种方法进行仿真。仿真结果对主动吸声以及主动隔声的研究具有指导意义和参考价值。

压电材料；主动吸声；主动隔声；驱动电压

研究人员研究出一种新型材料——压电复合材料。这种材料含有压电陶瓷和聚合物固体，具有相当强的压电性能，其密度比传统的压电材料低很多。压电复合材料在低密度介质中具有更好的声学耦合性能，可与水或者生物组织等匹配，无需铸造和磨削加工就可以用于非极性器械和传感器。压电材料也可以覆盖于结构物外部，从而形成声学阻抗表面。理论上,这种表面(通过适当的电极阵列)以电力驱动的方式使入射声波无法反射。具有声学阻抗表面的压电材料主要有两种用途：①用作单层换能器,防止声波的反射；②用作双层换能器，同时防止声波的反射和透射。研究人员已经对压电材料的性质进行了许多研究，将压电材料用于水听器和声纳阵列[1-6]。然而, 目前能够描述压电材料在声波反射或透射传播时驱动电压基本方程系数的文献较少。此外, 从复杂的弹性常数、介电常数和压电常数考虑，没有相关文献比较这些系数的测量值和计算值。本文旨在比较单层以及双层压电材料驱动电压的计算方法。

1 单层压电材料

单层压电材料的布置如图1所示。

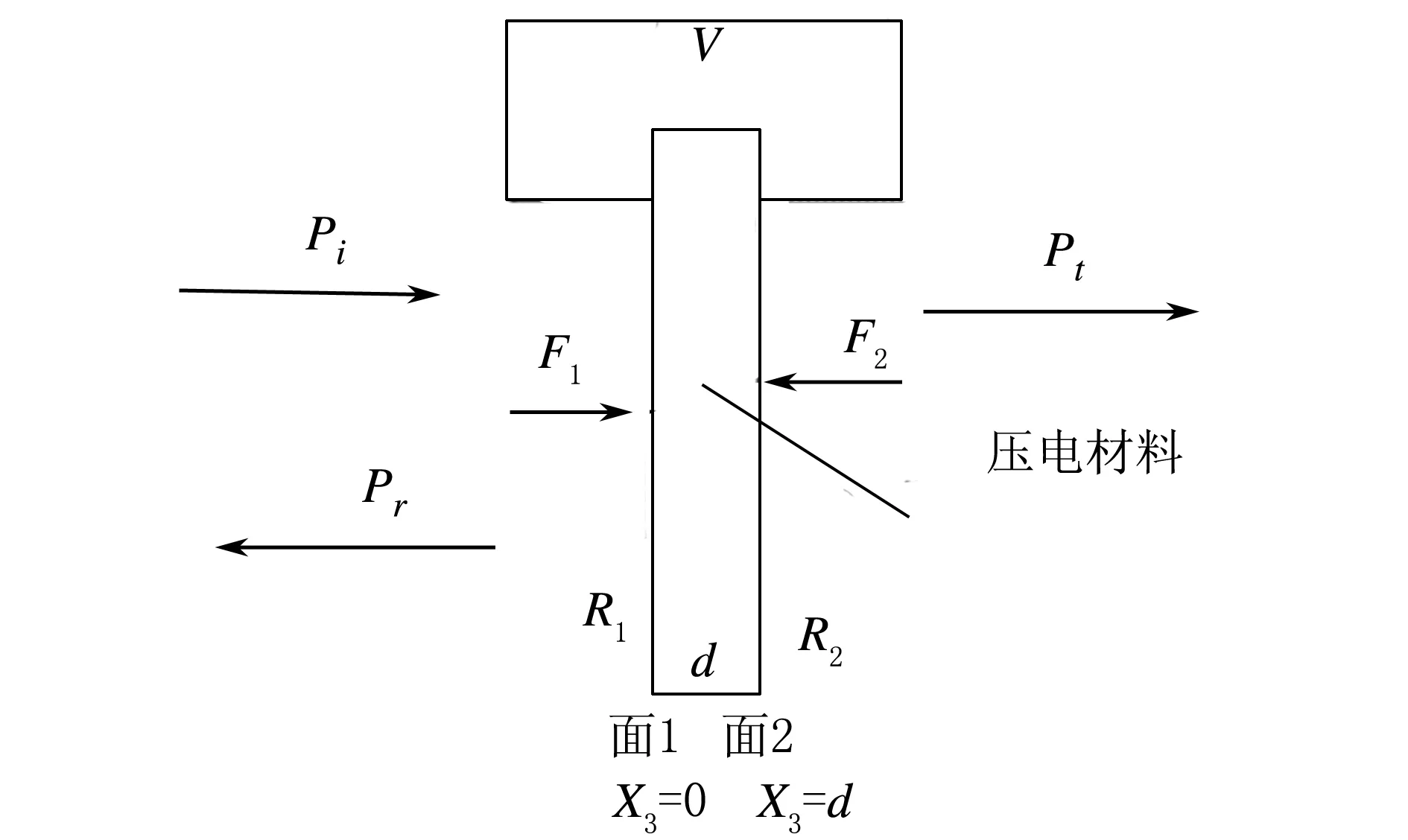
图1 单层压电材料的布置图

在图1中，Pi、Pr、Pt分别表示入射声压、反射声压、透射声压；F1、F2分别表示加在压电材料正面(面1)和反面(面2)上力的值；R1、R2分别表示压电材料正面和反面的声阻抗；V表示加在压电材料上的电压。

1.1 针对单层压电材料的理论法

有学者提出，根据薄型压电材料相对面所受的法向力与相对线速度的关系，可确定电压和电流是否通过压电材料。压电材料由一个不导电的压电层组成，其厚度d值远小于其表面的面积A值。在直角坐标系中，分别用x1、x2、x3表示3个相互垂直的坐标轴，并定义x3轴垂直于压电材料表面,其厚度在直角坐标系中表示为：x3=0(面1)至x3=d(面2)。

在压电材料面1上，时间t与力f1的关系为：f1(t)=F1ejωt。其中，t为时间，ω为圆频率。若其中力F1为复振幅，则可定义Fi和Ui(i=1,2)分别为压电材料表面法向力的复振幅和速度的复振幅，而且可定义V和I分别为加在压电材料上的电压复振幅和流过压电材料的电流复振幅。

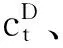
(1)

(2)

(3)

(4)

假设上述压电材料以面1和面2为界的两个半无限介质的声阻抗分别为R1和R2，一个平面声波垂直入射到面1，则F1是该入射声波和反射声波的叠加,F2则是该声波透射而产生的，有：

F1=(Pi+Pr)A0

(5)

F2=PtA0

(6)

(7)

(8)

将式(5)-式(8)代入式(1)-式(3)可得：

(9)

(10)

(11)

将式(9)-式(11)联立，可知压电材料的性能与Pi、Pr、Pt、V和J 5个不同的复振幅有关。如果给定其中两个复振幅值,就可求得方程式中剩余的3个复振幅值。设定Pi为所需的入射声波复振幅,且Pr=0,则：

(12)

(13)

(14)

1.2 针对单层压电材料的电声类比法

本文所用压电陶瓷的结构如图2所示。

图2 压电陶瓷的结构

在图2中,d是压电材料的厚度；U1、U2是压电材料在厚度方向的振动速度；F1、F2是作用于压电材料的压力；V是加在压电材料上的电压。在考虑压电陶瓷结构的基础上，可作出图2的等效电路(见图3)。

图3 压电陶瓷的等效电路

根据电路理论可推导出如下方程：

(15)

(16)

(17)

根据式(5)-式(8)，联立式(15)-式(17)，可得下列方程:

(18)

(19)

(20)

在式(18)-式(20)中，Pi、Pr、Pt、V、I为压电材料的5个复振幅。 如果给定其中两个复振幅值,就可求得方程式中剩下的3个复振幅值。设定Pi为所需的入射声波复振幅,且Pr=0,则转换后的方程如下:

(21)

(22)

(23)

根据式(21)-式(23),可求得加在压电材料上的电压，即：

(24)

由式(24)可知,改变加在压电材料上的电压，使得声波的反射波为零，能够达到主动吸声的目的。

比较式(12)-式(14)和式(24)可知, 电声类比法与理论法的计算结果是相同的。

1.3 针对单层压电材料的计算实例

(2)如果压电材料的厚度d变为2.5 mm，其他参数不变，则根据式(24)计算出加在压电材料上驱动电压的振幅和相位如图5所示。

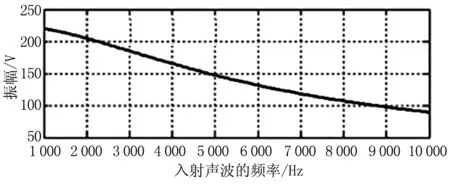
(3)如果压电材料厚度d变为3.5 mm，其他参数不变，则根据式(24)计算出加在压电材料上驱动电压的振幅和相位(如图6所示)。

从图4-图6可知，对于单层压电材料来说，要达到声波反射近于零，需要满足两点：①对于相同的压电材料，当其厚度减小且加在压电材料上电压的振幅和相位降低时,入射波频率增大；②当入射波的频率不变,加在压电材料上电压的振幅增大且相位降低时，压电材料的厚度增大。

(a)理论计算的驱动电压振幅

(b)理论计算的驱动电压相位图4 加在1.5 mm厚度压电材料上驱动电压的振幅和相位

(a)理论计算的驱动电压振幅

(b)理论计算的驱动电压相位图5 加在2.5 mm厚度压电材料上驱动电压的振幅和相位

(a)理论计算的驱动电压振幅

(b)理论计算的驱动电压相位图6 加在3.5 mm厚度压电材料上驱动电压的振幅和相位

2 双层压电材料

双层压电材料的布置如图7所示。

图7 双层压电材料的布置图

2.1 针对双层压电材料的理论法

这里研究的压电材料是由一层固定于面1，另一层固定于面2的两个压电层所制成的。相对于每层压电材料的方程组等价于式(1)-式(3)。考虑到压电材料两层特性的不同,对其特征量标注下标“1”和“2”予以区分。在新增附加边界条件下，两个接触面的受力和速度应是相等的。因此，每组方程的边界条件与7个复振幅有关,即：

D11Pi+D12Pr+d13Pt+D15J1+D17J2=0

(25)

D21Pi+D22Pr+D23Pt+D25J1+D27J2=0

(26)

D31Pi+D32Pr-V1+D35J1=0

(27)

D41Pi+D42Pr+D43Pt+D45J1+V2+D47J2=0

(28)

式中，表达式的复系数Dij在文末附录中给出。

在双层压电材料中，式(25)-式(28)形式上等同于单层压电材料中式(9)-式(11),其复振幅Pi、Pr、Pt、V1、J1、V2与复系数Dij有关。例如,设定Pi为所需的入射声波复振幅,且Pr=Pt=0,根据式(1)-式(3)和式(5)-式(8)可得出：

(29)

(30)

(31)

(32)

2.2 针对双层压电材料的电声类比法

根据双层压电材料的结构,可作出正面压电材料的等效电路图(见图8)。

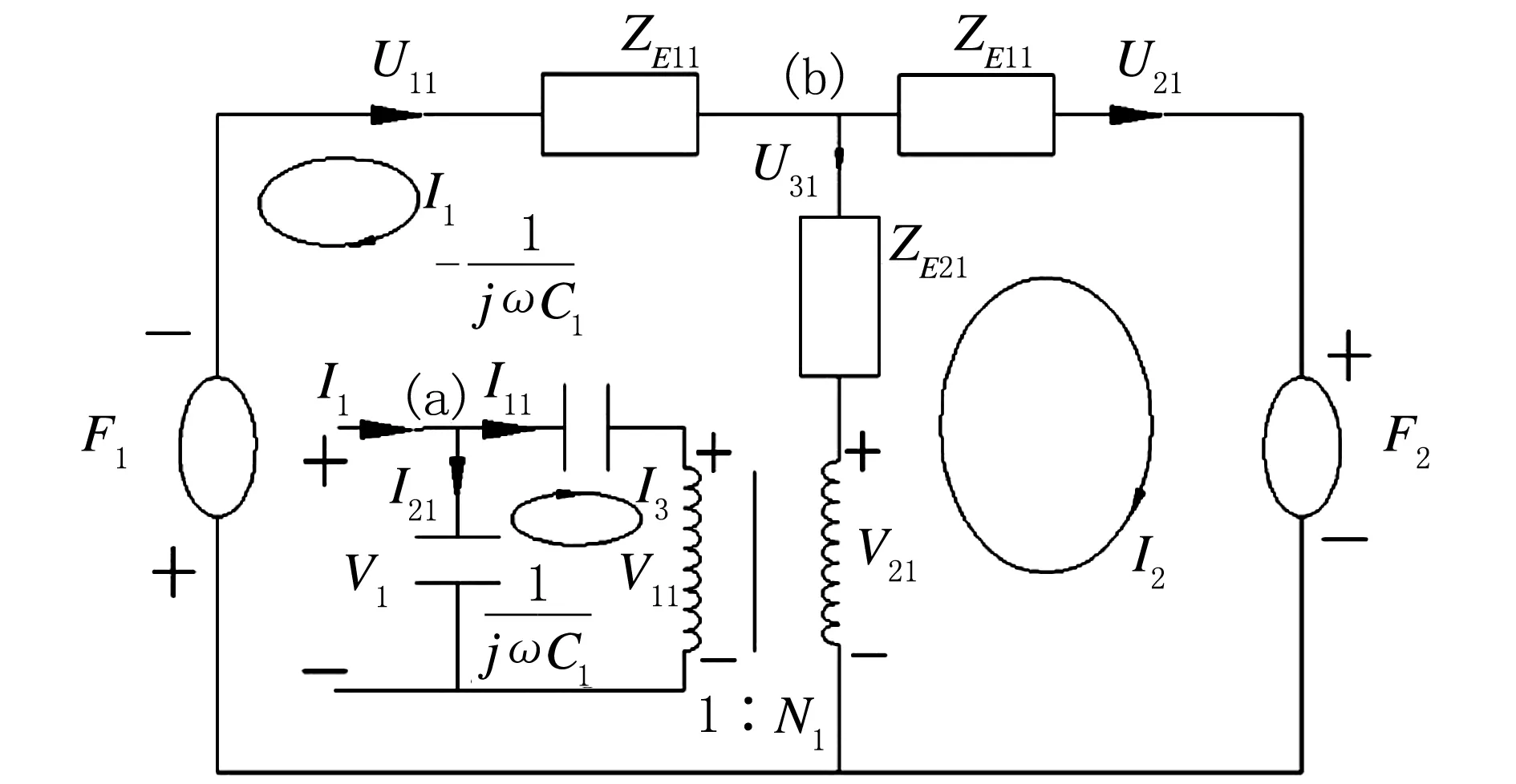
图8 正面压电材料的等效电路

(33)

(34)

(35)

同理，背面压电材料的等效电路如图9所示。

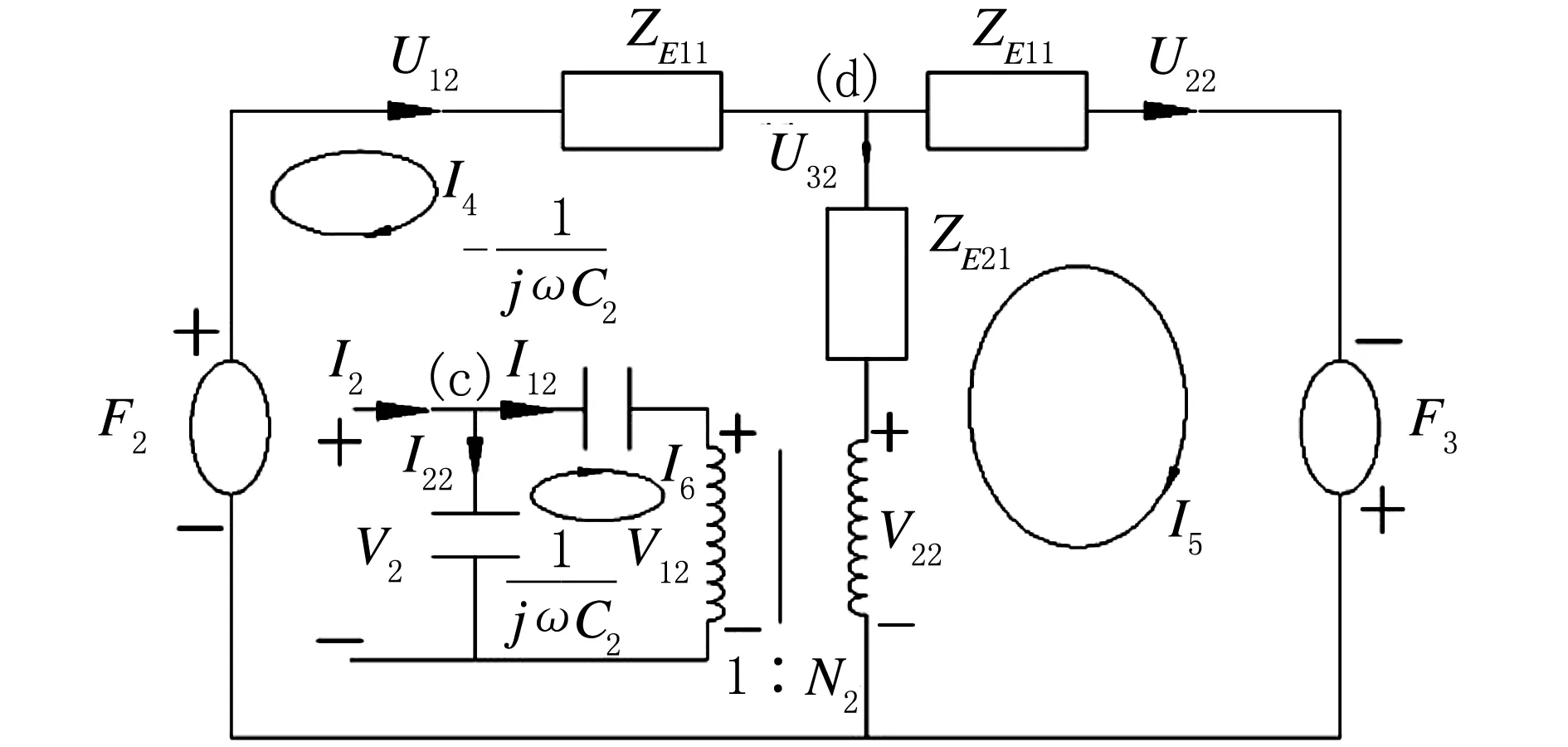
图9 背面压电材料的等效电路

(36)

(37)

(38)

由式(36)-式(38)可得到下列方程:

(39)

(40)

(41)

(42)

由式(39)-式(42)可知,改变加在压电材料上的电压，使得声波的反射波和透射波均为零，可以达到主动吸声和主动隔声的目的。

由式(29)-式(32)与式(39)-式(42)比较可知,电声类比法与理论法的计算结果是相同的。

2.3 针对双层压电材料的计算实例

(a)理论计算加在正面压电材料上的电压振幅

(b)理论计算加在正面压电材料上的电压相位图10 加在正面压电材料上的电压振幅和相位

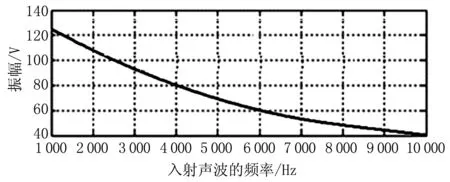
(a)理论计算加在背面压电材料上的电压振幅

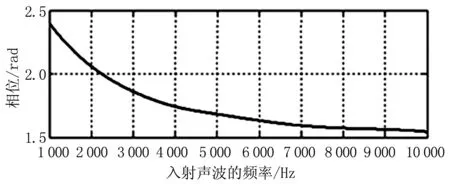
(b)理论计算加在背面压电材料上的电压相位图11 加在背面压电材料上的电压振幅和相位

3 结 语

为了比较单层主动吸声和双层主动吸声与隔声的压电材料表面的驱动电压，介绍了两种方法——理论法和电声类比法。计算实例表明,所提出的理论模型是正确和实用的。

附 录：

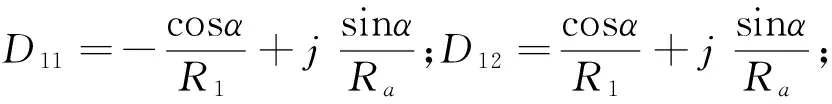
其中：α=k1d1；β=k2d2。

[1] Ting R Y. Characterization of the Properties of Underwater Acoustical Materials[J]. Journal of the Acoustical Society of America, 1989, 86(s1):299-303.

[2] Rittenmyer K M, Dubbelday P S. Determination of the Piezoelectric Properties Composite Materials by Laser Doppler Velocimetry[J]. Journal of the Acoustical Society of America, 1990, 88(s):114-116.

[3] Ting R Y. Recent Developments in Piezoelectric Composites for Transducer Applications[J]. Journal of the Acoustical Society of America, 1989, 85(s):60-62.

[4] Geil F G, Ting R Y. Application of Piezoelectric Composite for Large Area Hydrophone Arrays[J]. Journal of the Acoustical Society of America, 1988,84(s):68-69.

[5] 朱从云，李晓娟，鲁付杰，等.一种主动消声器的工作原理分析[J].中原工学院学报，2015，26(6)：21-26.

[6] Rittenmyer K M. Temperature Dependence of the Electromechanical Properties of Ceramic Polymer Composite Materials for Hydrophones Application[J]. Journal of the Acoustical Society of America, 1988, 83(s):81-83.

[7] Berlincourt D A, Curran D R, Jaffe H. Piezoelectric and Piezomagnetic Materials and Their Function in Transducer[J]. Physical Acoustics,1964,105:169-270.

[8] Moon W, Busch-Vishniac Ⅰ J. A Finite-element Equivalent Bond Graph Modeling Approach with Application to the Piezoelectric Thickness Vibrator[J]. Journal of the Acoustical Society of America, 1993, 93(6):3496-3506.

[9] Hazony D. Piezoelectric Transducers with Ideal Time Limited Impulse Response[J]. Journal of the Acoustical Society of America, 1981, 70(3):661-662.

[10] Stefano M, Vittorio P. Porous Piezoelectric Ceramic Hydrophone[J]. Journal of the Acoustical Society of America, 1999,106 (2): 456-475.

[11] Hikita K, Yamada K, Nishioka M,et al. Piezoelectric Properties of the Porous PZT and Porous PZT Composite with Silicone Rubber[J]. Ferroelectrics, 1983,91(4):265-270.

[12] Wen J, Hsueh. Novel Graph Model and Analysis Method for Piezoelectric Thickness-drive Transducers[J]. Journal of the Acoustical Society of America, 1987, 108(5):225-265.

[13] Bao X Q,Varadan V K,Varadan V V, et al. Model of a Bilaminar Actuator for Active Acoustic Control Systems[J]. Journal of the Acoustical Society of America, 1990,87(3): 875-898.

[14] Howarth T R, Vijay K, et al. Piezo-composite Coating for Active Underwater Sound Reduction[J]. Journal of the Acoustical Society of America, 1999,91(2): 556-565.

[15] Tzou H S, Gadre M. Active Vibration Isolation and Excitation by a Piezoelectric Slab with Constant Feedback Gains[J]. Journal of Sound and Vibration, 1990,136(2): 447-490.

[16] Smith W A. Composite Piezoelectric Materials for Medical Ultrasonic Imaging Transducers-A Review[C]//Proceedings of the Sixth IEEE International Symposium on Applications of Ferroelectrics. Washington:IEEE,1986: 249-256.

(责任编辑：王长通)

Computation of the Driving Voltage Applied Across the Lay in Single and Double Layers of Piezoelectric Material for Active Sound Absorption

ZHU Cong-yun1, ZHU Ji-hua1, ZHU Yong-zhi2, HUANG Qi-bai3

(1.Zhongyuan University of Technology, Zhengzhou 450007;2. Henan Senyuan Heavy Industries Co.,Ltd., Changge 461500;3. Huazhong University of Science and Technology, Wuhan 430074,China)

Piezoelectric material can be used as a main component of devices, such as transducers, energy exchangers and arresters. Due to its excellent mechanics and electric coupling performances, piezoelectric material can also be utilized in control system of sound and vibration. However, there have not been any publications outlining the basic equations of reflection or transmission coefficients of driving voltage applied across the layers (single or double) of piezoelectric material. In this paper, two methods-the theoretical method and the electro-acoustic analogy method are used in order to compare the driving voltage applied across the single and the double layer of active sound surfaces of piezoelectric material. Computational results indicate that the proposed theoretical models are correct and applicable in practical implementations.

piezoelectric material；active sound absorption；active sound isolation； driving voltage

2015-08-02

国家自然科学基金项目(51175195)；河南省高等学校重点科研项目(15A460041)

朱从云(1971-), 男, 江苏扬州人, 副教授,博士,主要研究方向为振动与噪声控制。

1671-6906(2016)06-0010-07

TU55

A

10.3969/j.issn.1671-6906.2016.06.003