风力机翼型多学科优化设计方法研究
郭小锋, 杨树峰, 车江宁
(中原工学院, 郑州 450007)
风力机翼型多学科优化设计方法研究
郭小锋, 杨树峰, 车江宁
(中原工学院, 郑州 450007)
提出了一种基于翼型集成理论的钝尾缘翼型集成表达方法。针对风力机中低厚度翼型的气动、结构及噪声等多学科设计要求,采用粒子群算法构建了翼型的优化设计模型。以翼型最强气动性能为目标,在满足几何约束、结构及噪声学学科性能要求下,设计出具有良好气动性能、结构特性、噪声特性、失速特性和粗糙度敏感性的新翼型CQU-B210。计算分析结果表明,CQU-B210的各项性能指标均比常用翼型DU-210型有较大提高。
风力机翼型;气动性能;结构特性;气动噪声;优化设计
翼型是风力机叶片外形和结构设计的基础,良好的风力机专用翼型应具备良好的气动性能和结构特性、平缓的失速特性以及粗糙度不敏感性[1-2]。
随着风轮直径的增大,风力机所产生的噪声增大,对周围居民和环境带来的影响阻碍着风力机的进一步发展。位于叶片叶尖前半段的中低厚度翼型是风力机气动噪声的主要发生源。设计中,应在改善风力机叶片中低厚度翼型气动性能、结构特性的同时,降低其噪声指标[3-4]。
针对这些问题,本文提出了基于翼型集成理论的钝尾缘翼型参数化表达方法;基于粒子群算法,提出了综合考虑翼型气动、结构和噪声特性的风力机翼型多学科优化设计方法;优化设计了CQU-B210型新翼型,并与常用翼型进行了对比分析。
1 翼型集成表达
1.1 尖尾缘翼型转换

图1 翼型坐标转换图

f(zc)=zc+a2/zc
(1)
式中,a为拟圆矢径。
基于西奥道生思想,提出一种拟圆的表达方法,将zc表示为:
zc=aρ(θ)exp(iθ)
(2)
式中,ρ(θ)为翼型的形函数。形函数可表示为Taylor级数形式:
ρ(θ)=c1+c2θ+c3θ2+c4θ3+…+ckθk+…
(3)
在翼型的优化设计中,取式(3)前11项,改变这11项系数,就可以得到无穷多种尖尾缘翼型[5]。
1.2 钝尾缘翼型参数化表达
运用集成表达方法生成的翼型为尖尾缘翼型。为了增加叶片尾缘的强度,在叶片实际设计中运用的是钝尾缘翼型。因此,本文采用式(4)对尖尾缘翼型进行尾缘渐进对称增厚处理[6-7]。
(4)
式中:x和y分别为尖尾缘翼型上下翼面的横坐标和纵坐标;ax为翼型最大相对厚度位置的横坐标;p为尾缘的厚度增加值;n为翼型增厚指数因子,这里取值为2;x′和y′为尾缘增厚之后的新翼型坐标。按式(4)对基于集成表达理论生成的尖尾缘翼型进行尾缘渐进对称增厚处理,得到的钝尾缘翼型如图2所示。
注:弦向坐标和纵向坐标均为无量纲比值。图2 钝尾缘翼型图
2 翼型的多学科设计性能
2.1 气动性能
风力机在实际工作中受到风沙、昆虫的侵蚀,其叶片初始设计的光滑表面在运行过程中会变得粗糙。因此,在翼型设计中应考虑光滑和粗糙两种工况,翼型在两种工况下升阻比系数越大越好。
RFOIL软件是由荷兰国家能源研究中心(Energy Research Centre of the Netherlands)开发的一款专用于风力机的翼型气动性能分析软件,其计算过程与常用的XFOIL软件类似[8],可以被Matlab程序编程调用。与XFOIL软件相比,RFOIL软件的主要优点是针对风力机的工作特点,改进了翼型失速区域气动性能分析的稳定性和准确性。本文将使用RFOIL软件对所设计翼型进行气动性能分析。
2.2 结构特性
由悬臂梁理论可知,叶片的截面刚度越大,叶片抵抗弯曲变形的能力越强,而叶片的截面刚度又与翼型面对弦长的惯性矩成正比。在不考虑复合材料铺层的情况下,以翼型面对弦长的惯性矩作为翼型结构特性的评价指标,依据叶片实际铺层情况,设定翼型截面的翼面厚度为0.01 m,并通过积分求取翼型截面对弦长的惯性矩Ixx。
2.3 噪声特性
美国可再生能源实验室的Brooks、Pope和Marcolini提出了一种半经验的翼型噪声计算模型(BMP模型),将翼型的噪声分为尾缘噪声(TBL-TE)、失速噪声(SEP)、层流涡噪声(LBL-VS)、叶尖噪声(TIP)、钝尾缘噪声(TEB-VS),并给出了这5种噪声的计算公式[9]。
BMP模型中翼型的边界层参数是基于NACA-0012翼型试验数据得到的经验数据。为了计算翼型不同工况的噪声特性,需要对翼型的边界层参数计算方法进行改进。本文使用RFOIL软件通过耦合求解位流方程和边界层方程,转捩判断基于层流稳定性理论的e-N方法,处理自由转捩和固定转捩问题,求解翼型各种流动情况的气动参数,包括翼型的边界层参数,其计算结果准确可信。基于此,本文将BPM模型中用经验公式求解翼型边界层的方法改为用RFOIL软件来求解,从而拓宽原噪声模型的适用范围,同时提高计算的准确性。翼型的边界层参数可以表示为雷诺数、攻角、湍流度等流动参数的函数,即:
δ=f(Re,α,tur)
(5)
通过设定相应的雷诺数Re、马赫数Ma、攻角α、湍流度tur,可以得到翼型的边界参数文件。读取文件中与噪声有关的计算参数,代入翼型噪声计算模型,就可求得噪声值。
这里以NACA64418翼型为例进行噪声计算分析方法的说明。其相关参数如下:
声速:c0=340 m/s;翼展长度:d=1 m;
黏性系数:μ=1.5×10-5;翼型弦长:C=0.4 m;
空气密度:ρ=1.225 kg/m3;攻角:α=6°;
来流速度:V0=70 m/s;尾缘钝度:0.000 2 m;
观测距离:r=1.2 m;钝度角:Ψ=12.5°;
观察角度:θ=90°。
2.4 翼型噪声的计算过程
(1)采用RFOIL软件计算翼型的气动性能,得到边界层参数δ的计算结果(见图3)。

注:Distr_up和Distr_lo分别为翼型的 压力面边界层计算结果和吸力面边界层计算结果。图3 翼型边界层计算结果
(2)将提取的边界层参数导入噪声计算模块,进行翼型的噪声计算。
(3)提取总的噪声计算结果,绘制噪声特性曲线。
图4所示为NACA64418翼型在光滑和粗糙工况下的总噪声计算结果。

注:边界层条件为Re=6.0×106, Ma=0.15,α∈[0°,20°]。图4 NACA64418翼型噪声计算结果
3 优化设计模型
3.1 优化目标
以翼型在攻角α处光滑与粗糙两种情况的升阻比最大为优化设计目标,在雷诺数Re=6.0×106和马赫数Ma=0.15的条件下,翼型优化设计的目标函数可表达为:
(6)

3.2 设计变量
根据翼型形函数的表达方程式(3),选择ρ(θ)的前11项系数集成表达翼型。此外,以变量P表示翼型尾缘的厚度,则设计变量可记作:
X=(c1,c2,c3,c4,c5,c6,c7,c8,c9,c10,c11,P)
(7)
3.3 约束条件
(1) 几何约束:在翼型设计时,为避免翼型出现与设计要求不符合及尾缘交叉等问题,对翼型的最大弯度、最大厚度及其发生位置等进行约束[5]。
(2)结构特性:以翼型截面对弦长的惯性矩Ixx作为翼型结构特性的评价指标,Ixx越大越好。
(3)最大噪声的控制:基于上文的噪声计算模型,对翼型的噪声特性作如下约束:
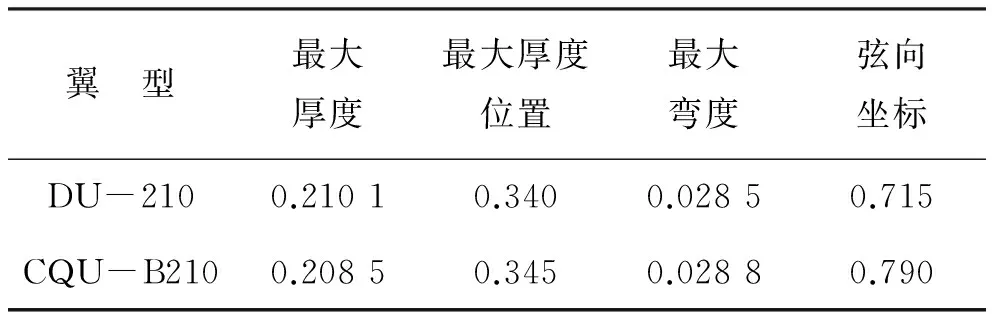
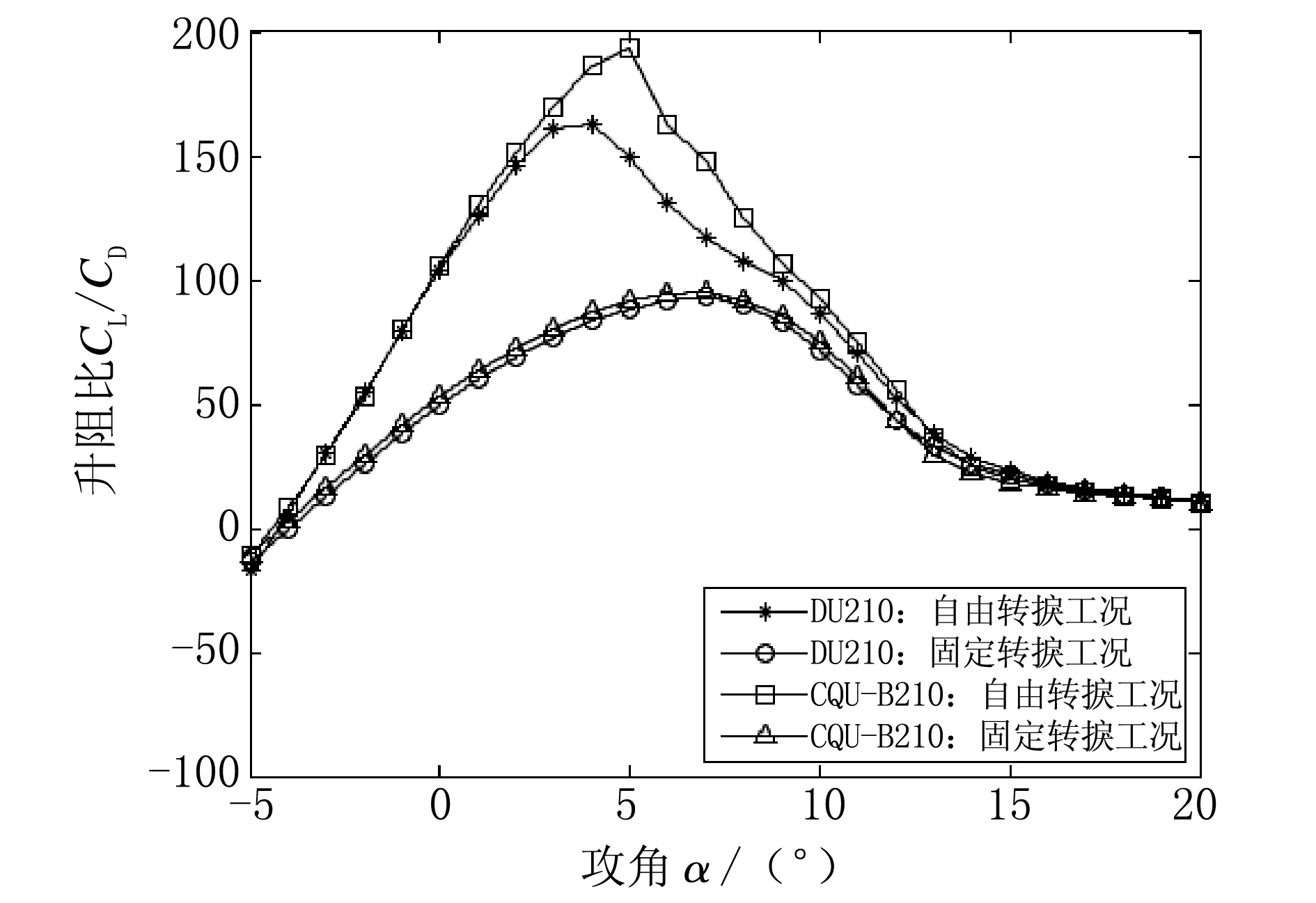
SPL (8) 噪声的度量采用加权声功率级SPL(Sound Power Level)。其计算参数为:翼型的当地风速为v0;观察距离r=1 m;观察角度为90°;翼型弦长C=1 m;翼展长度d=1.3 m。翼型噪声的约束值N通常参考翼型相同设计工况的数据求得,是一个经验值。 3.4 优化算法 在翼型的多学科设计要求中,气动性能是主要方面,结构特性及气动噪声可作为学科性约束,使优化设计得以简化,从而可采用单目标粒子群算法[10]。对于每一个集成表达的钝尾缘翼型,调用RFOIL软件来计算翼型的气动性能,调用结构特性程序来计算翼型惯性矩模量,调用噪声特性程序来计算翼型的噪声指标,并根据约束条件计算出个体的计算适应度值。每一代个体计算完成后,对粒子群算法的计算参数进行自适应调整,以避免优化程序的过早收敛。粒子群算法中相关参数的设置如下:种群大小取40;粒子维数取13;进化代数为150。 采用上述中低厚度翼型优化设计方法设计的CQU-B210型翼型如图5所示。 注:弦向坐标和纵向坐标均为无量纲比值。图5 翼型形状对比 两个翼型的几何特性对比如表1所示。为了验证所设计翼型的性能,对翼型的气动性能、结构特性和噪声特性进行了计算分析,并与常用厚度为0.21的DU-210型翼型进行了比较。图6所示为CQU-B210型新翼型与DU-210型翼型在相同条件下(Re=6.0×106,Ma=0.15)气动性能的对比分析。 表1 翼型的几何特性对比 注:表中数据均为无量纲比值。 从图6可以看出,在主要攻角范围内,无论是在粗糙条件还是光滑条件下,新翼型的升力系数及升阻比均比DU-210型翼型的高。 表2所示为CQU-B210型翼型与DU-210型翼型的气动性能参数对比。从表2可以看出,相对于DU-210型翼型,在自由转捩工况下,新型翼型最大升力系数为1.600 7(攻角12°的位置),提高了2.61%,最大升阻比为193.21(攻角5°的位置),提高了19.03%;在固定转捩工况下,新型翼型最大升力系数为1.547 4(攻角12°的位置),提高了1.71%,最大升阻比为95.54(攻角7°的位置),提高了2.64%。显然,新型翼型具有更好的气动性能。从翼型的升力曲线看,新型翼型与DU-210型翼型一样具有良好的失速平缓特性。 (a)升力系数 (b)升阻比 (c)阻力系数图6 翼型气动性能对比 图7所示为自由转捩工况与固定转捩工况下CQU-B210型与DU-210型翼型噪声计算值随攻角的变化曲线。从图7可以看出,在自由转捩工况和固定转捩工况下,优化设计翼型的噪声计算值在失速之前明显低于DU-210型翼型,在失速之后基本上与DU-210型翼型持平。 在自由转捩工况下,CQU-B210型翼型的最大噪声值比DU-210型翼型的最大噪声值减小了1.48 dB;在固定转捩工况下,前者比后者减小了0.31 dB。这表明CQU-B210型翼型比DU-210型翼型具有更好的噪声特性。 表2 翼型气动性能参数对比 注:括号内表示最大升力系数、最大升阻比的攻角位置;噪声数据表示固定转捩工况下最大升阻比时对应攻角的计算值。 (a)自由转捩工况下翼型噪声指标对比 (b)固定转捩工况下翼型噪声指标对比图7 翼型噪声指标对比 此外,从翼型结构特性对比上看,DU-210型翼型的惯性矩为1.147 1×10-4,而优化设计的CQU-B210型翼型为1.154 3×10-4,提高了0.63%,这表明新翼型也具有较好的结构特性。 在翼型的表达方法上,本文提出了一种基于翼型集成理论的钝尾缘翼型集成表达方法,对集成表达生成的尖尾缘翼型从最大相对厚度处开始进行渐进对称增厚处理,解决了现有集成理论中翼型尾缘钝化处理影响翼型气动性能的问题。 本文研究了翼型噪声的评估方法,提出了一种基于噪声的风力机中低厚度翼型多学科优化设计方法,以翼型的气动性能最佳为优化目标,以翼型的结构参数、噪声为约束条件,优化设计了具有良好气动性能、非设计工况特性、粗糙度敏感性和失速特性的CQU-B210型风力机中低厚度翼型族。 [1] Timmer W A,Rooij V. Summary of the Delft University Wind Turbine Dedicated Airfoils[J]. Journal of Solar Energy Engineering, 2003, 125(4): 11-21. [2] 陈进, 郭小锋,李松林. 风力机大厚度钝尾缘翼型优化设计方法[J]. 哈尔滨工程大学学报,2015,36(3):130-136. [3] Cheng J T, Zhu W J, Fischer A, et.al. Design and Validation of the High Performance and Low Noise CQU-DTU-LN1 Airfoils[J]. Wind Energy, 2014, 17(12) : 1817 -1833. [4] Bjork A. Coordinates and Calculations for the FFA-W1-xxx, FFA-W2-xxx and FFA-W3-xxx Series of Airfoils for Horizontal Axis Wind Turbines[R]. Stockholm,Sweden:FFA TN, 1990. [5] 陈进, 张石强,Eecen P J,等. 风力机翼型参数化表达及收敛特性[J]. 机械工程学报,2010,46(10):132-138. [6] 邓磊, 乔志德,杨旭东,等. 基于RANS方程大型风力机翼型钝尾缘修型气动性能计算[J]. 太阳能学报,2012,33(4):545-551. [7] 张磊,杨科,赵晓路. 不同尾缘改型方式对风力机钝尾缘翼型气动性能的影响[J].工程热物理学报,2009,30(5):773-776. [8] Thomas F B, Stuart P D, Michael A. Marcolini Airfoil Self-Noise and Prediction[R]. Washington, USA:NASA Reference Publication 1218, National Aeronautics and Space Administration, 1989. [9] Chen J,Wang Q, Shen W Z, et al. Structural Optimization Study of Composite Wind Turbine Blade [J]. Materials & Design, 2013,46(4):247-255. [10]李丽,牛奔.粒子群优化算法[M].北京:冶金工业出版社,2009. (责任编辑:王长通) Multidisciplinary Design Optimization of the Wind Turbine Airfoils GUO Xiao-feng, YANG Shu-feng, CHE Jiang-ning (Zhongyuan University of Technology, Zhengzhou 450007, China) In this paper, the functional integral theory of blunt trailing edge wind turbine airfoils is studied. Aiming at the problem of a well-designed airfoil need satisfying multidisciplinary design requirements such as aerodynamic, structural and noise, a optimization design model is developed based on PSO algorithm. The optimization goal is the best aerodynamic performance, while satisfying geometric constraint, structural and noise requirement, a new airfoil named CQU-B210 which has better aerodynamic performance, structural characteristics, noise performance, stall and roughness sensitivity characteristics is optimized, comparing with a wind turbine airfoil (DU-210),the analysis shows that the optimized airfoil has better performance on every aspects. wind turbine airfoil; aerodynamic performance; structural characteristics; noise; optimization design 2016-10-13 河南省高等学校重点科研项目(16A460041) 郭小锋(1983-),男,河南西峡人,讲师,博士,主要研究方向为风力机叶片优化设计理论及方法。 1671-6906(2016)06-0022-06 TK83; TH12 A 10.3969/j.issn.1671-6906.2016.06.0054 优化设计结果






5 结 语

