用问题驱动教学模型实施计算思维教学的应用与实践

摘要：实施有效的计算思维教学是当前计算思维的研究重点之一。文章提出将计算思维的思想方法与问题驱动教学模型结合起来，构建一种融入计算思维理念的问题驱动教学模型，并说明如何基于该模型开展计算思维教学实践。同时，结合课程案例分析计算思维在教和学过程中的作用，验证该模型的可用性与有效性。

关键词：问题驱动教学；计算思维；教学模型；教学案例

1.背景

计算思维的含义是运用计算机科学的思维方法进行问题求解、系统设计以及理解人类的行为，它涵盖计算机科学领域的一系列思维活动，目的是培养一种独特的思考习惯与思维方式口]。自2006年美国卡内基·梅隆大学的周以真教授提出计算思维以来，这一概念在大学计算机教学领域被广泛研究与探讨。2012年，计算思维的发展大体经历了概念产生、研究与探讨、实施计算思维教学3个阶段；2014年，李廉教授提出计算思维的两个特质——可解释证明和关联世界。至此，计算思维的认识上升到一个新的高度。

研究计算思维的目的是在教学中开展计算思维教育，培养学生计算思维能力，为提高创新能力奠定基础。实施计算思维教学的工作主要包括以下几方面：①计算思维教学的基础平台建设；②基于计算思维教育的课程体系；③构建多元化思维学习环境；④计算思维教学方法与手段的改革。

2.问题驱动教学模型

2.1问题驱动教学模型的概念

问题驱动教学是以问题为中心的教学方式，教师在教学中充当启发者和指导者，提出问题并创设情境，让学习者紧紧围绕问题去寻找解决办法。学习者自主学习、主动探究，在此过程中形成发散思维，提高自身综合素质。问题驱动教学符合计算思维构造的特征，易于实施计算思维教学。

2.2问题驱动教学模型的描述

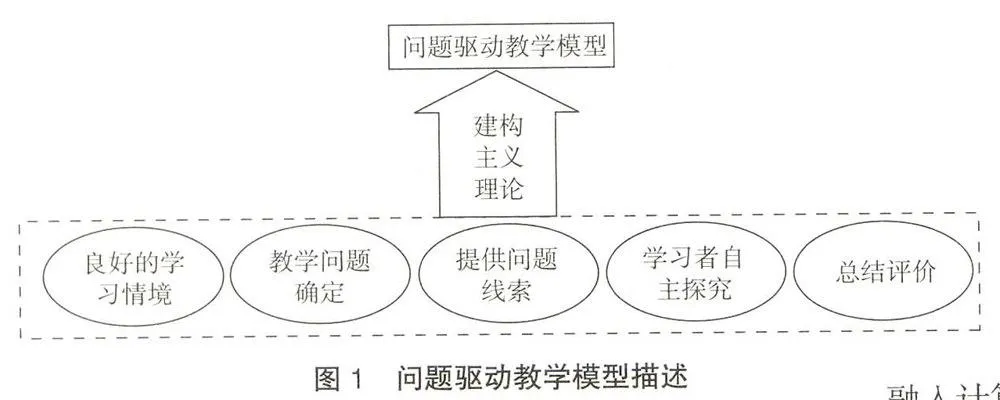
问题驱动教学的根本是解决问题，其灵魂在于学习者的自主学习能力。根据建构主义学习理论，学习者可以通过主动建构，主动参与、探索问题的解决方法，改变传统课堂“满堂灌”的方式。教学者引导学习者主动建立认知结构，形成科学思维思想，提高自身解决问题与分析问题的能力。问题驱动教学模型涉及的对象包括教学者和学习者，工作过程可以描述为以下5个方面，如图1所示。

（1）教学者：提供一个良好的、生动有趣的适合问题驱动教学实施的学习情境。

（2）教学者：根据教学内容设计一个好的问题或一个相关联的“问题链”。

（3）教学者：提供问题的线索，引发学习者的兴趣，引导学习者进行自主的探索学习，寻找解决问题的方法。

（4）学习者：自行寻找问题解决方法，与其他人共同讨论，通过学习者之间的互动交流，加深问题理解，修改及补充习得的知识和技能。

（5）教学者：评价学习者在探索过程中的表现，并检测他们的习得结果和求解方法。

3.融入计算思维的问题驱动教学模型

3.1计算思维思想及在问题驱动教学模型中的作用

计算思维是一种包含全部科学思维特征的思维方法，其范围已经超越计算学科，还与社会计算、计算物理、计算化学等学科融合，最终实现利用计算工具、思想、方法和技术以及计算环境和资源，培养学习者的思维能力、应用能力与创新能力。

将计算思维思想融于问题驱动教学模型，以问题设计作为教学的核心，可以引导学习者在解决问题的过程中使用抽象、分解、约简、递归、仿真等计算思维方法，主动理清相关事物间的关联因素，提高自身的思维能力。运用计算思维的方法解决学习、生活中的问题，这种教学模式符合大学计算机课程的教学目标，并为其他学科的课程提供借鉴。

问题驱动教学模型较少关注学习者在求解问题过程中使用的方法和规则，也少有思维训练的内容。探索以思维为核心的问题驱动教学模型，延伸与发展问题驱动教学理论，也促进计算思维自身的发展和应用。

3.2融入计算思维的问题驱动教学模型描述

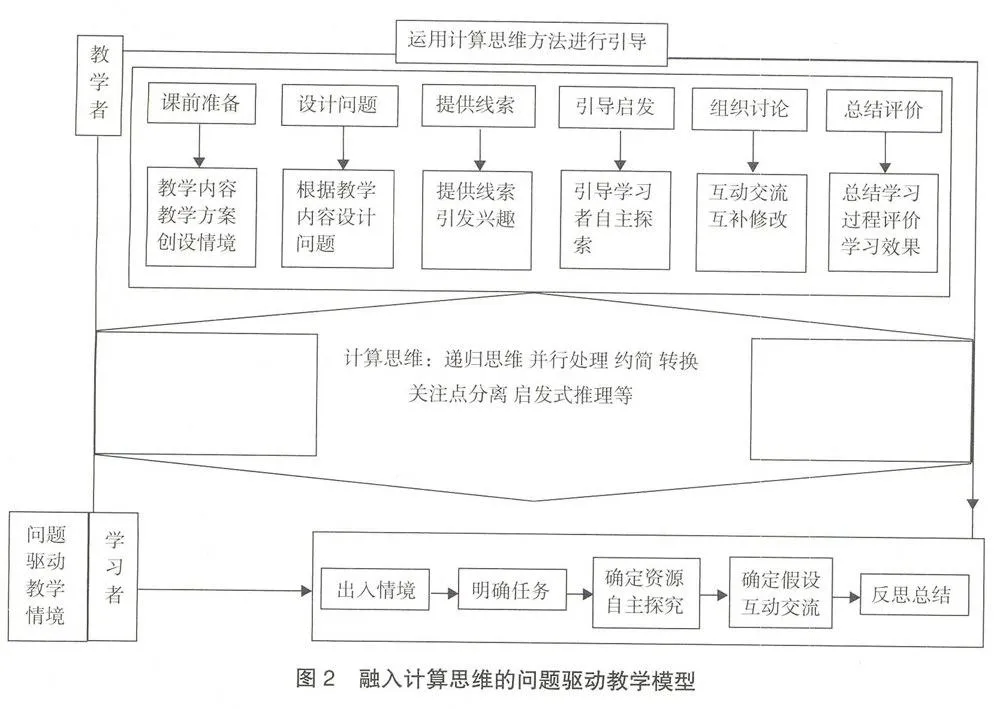
融入计算思维的问题驱动教学模型包括3部分：教学者活动、学习者活动、计算思维方法。

（1）教学者活动。教学者为学习者创建良好的学习情境，按照计算思维思想完成课前的相关准备工作，包括设计问题、提供线索、引导启发学习者自主思考、组织讨论以及评价总结等工作。

（2）学习者活动。包括进入学习情境、明确任务、查询资源并自主探究、互动交流和反思总结等工作。学习者在学习过程中为了解决问题进而自主地探索学习，与教学者及其他的学习者合作、互动，根据需要进行资源检索，并按照自己喜欢的方式学习。学习者在教学者的引导下自主学习，采用计算思维的方法建构知识点，寻求适合求解问题的方法，从而更好地解决问题。

（3）计算思维方法。计算思维方法贯穿问题驱动学习过程的始终。教学者引导学习者自主探索，学习者在求解问题的过程中使用计算思维方法，并在获取知识的过程中进行反思，形成科学的思维观。教学模型如图2所示，可以看出，计算思维方法贯穿整个教学过程，是全过程的核心。根据问题驱动教学模型而开展的教学活动，都是围绕着计算思维而展开的。

4.案例

哥尼斯堡七桥问题是计算机类专业离散数学和数据结构课的一个基本问题，也是大学计算机课程中问题抽象与数学建模的一个典型问题。该案例可拓展性强，可以推广到其他类似知识点的教学中去。本案例设计依据融入计算思维的问题驱动教学模型，对部分内容做了微调。

1）教学目标。

属于课前准备工作，本案例的目标定位如下。

（1）利用计算思维方法实施本课教学，学生应清晰掌握问题抽象与数学建模的含义；

（2）学生应掌握“哥尼斯堡桥”可以解决哪些类似问题，并且能够使用无向图对这些问题进行建模；

（3）在应用实践中，能够用类似方法完成一般问题的抽象与建模，包括典型的“一笔画”问题求解，力求理解加权路径问题。

通过前期准备界定上述教学目标后，学生在课程学习时就可以确定学习重点，即“哥尼斯堡桥”问题的本质是什么？如何抽象建模？怎样扩展类似问题？能否给出算法或编程实现？

2）教学设计。

（1）引入问题，设计案例。以著名古典数学问题哥尼斯堡桥七桥问题引出教学内容，有利于激发学生的学习兴趣，进一步开展抽象、数据描述、归纳等思维训练。

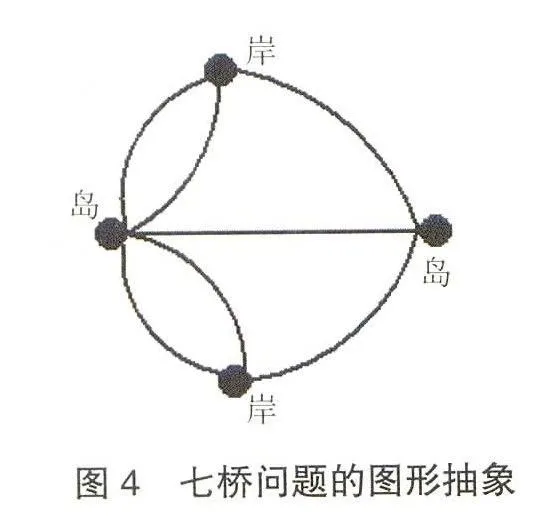
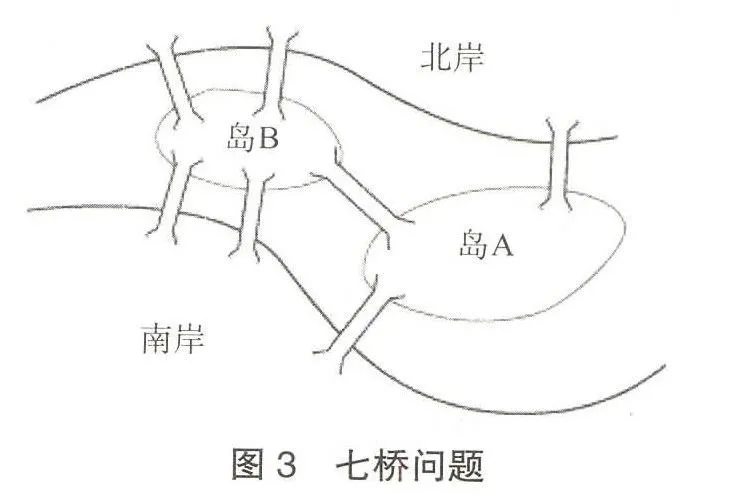
题目描述：18世纪初普鲁士的哥尼斯堡的一个公园里，普雷格尔河从中穿过，河上有两个小岛，有7座桥把河中两个小岛及河岸连接起来，如图3所示。能否从这4块陆地中任意一地点出发，恰好通过每座桥一次，再回到起点？我们如何解决这个问题？

（2）课前摸底，提供线索。

设计课前摸底问题：哥尼斯堡七桥问题的本质问题是什么？数学抽象与建模的意义何在？学习者是否了解树和图的概念？什么场合使用图？图有哪些存储方法？图的特点是什么？

这些问题既可以体现知识的前后关联，也便于教师决定在讲授具体问题时，是只局限于一部分概念还是需要深入教学，包括从哪个层次和角度开展深入教学。

（3）教师参与学习，引导启发。

参与式学习可以让学生自主地加入教学过程，改变传统的被动式学习方式，体现“以学生为中心”的教育理念。运用问题驱动式教学方法，引起学生兴趣，启发学生思考，能够很好地调动学生的学习积极性。在该案例中，通过启发，学生最终形成的七桥问题抽象结果如图4所示。

（4）组织讨论。

在讲完“哥尼斯堡七桥”的概念及图形抽象后，可以启发学生思考：如果路径更为复杂，在抽象后的图形中，如何判断每条路径只能通过一次？接着，启发学生讨论“一笔画”问题。再进一步引入加权图问题、最短路径问题。这一系列问题融入了转换、抽象、关联、演绎等思维方法训练。通过这种问题驱动的方式，由学生自主探究思考，更深层地进入学习情境，最终完整地掌握所有知识的结构和细节。

（5）效果评估。

效果评估与学习目标相呼应，设计面向不同目标的测试题目，范围覆盖树和图的基本概念、抽象与数学建模思想、算法描述与实现等内容。效果评估需要对应引入的案例，设计比较问题引导学生深入学习，分析抽象与数学建模的本质，剖析蕴含的设计思想。通过评估，整个课程教学前后呼应，强化了课堂教学的整体性。

（6）总结评价。

结合本教学案例与课程设计，指出化解课程难点和重点的方法，实现将计算机科学教育与计算思维方法结合，并根据教学内容的特点开展人文素养教育。

3）教学模型的应用效果分析。

为了了解融入计算思维的问题驱动教学模型的教学效果，笔者按“认识-应用-理解-最终效果”4个维度递进分析。4个维度描述如下：一是学生对计算思维的认识度；二是计算思维思想应用在问题驱动教学模型中，学生对教学过程的认可度；三是哪些课程适合采用计算思维思想方法；四是学生自主学习兴趣的提升度。教学效果反馈的方式是访谈和问卷。以问卷为例，共发放101份问卷，回收有效问卷95份，反馈结果如下。

（1）通过设计一些和计算思维相关的具体典型问题，最终能够理解计算思维含义的学生占88.9%。

（2）哥尼斯堡七桥问题引入计算思维方法后，认为对学习过程有较大帮助的学生占41.1%，认为有帮助的占31.6%，说明计算思维的认识及推进、问题驱动教学模型的改进还有很多工作要做。

（3）能够列举出3门以上可以使用计算思维方法的课程的学生占50.0%，2门课程的占23.2%，说明学生仔细思考了课程教学中的计算思维方法，达到了预期教学效果。

（4）认为问题驱动教学中引入计算思维方法后可以有效提升学习的自觉性与兴趣的学生占65.3%。

可以看出，问题驱动教学过程中，通过用转换、抽象、关联等计算思维方法，学生已经形成初步认识，并在一些课程中有了潜在的应用。在问题驱动教学过程中突出计算思维的思想，在思维层面梳理知识之间的内在联系，清晰渗透学科思想方法，能够培养学生形成良好的思维方法与解决问题的能力。

5.结语

在教学过程中，使用计算思维的思想方法，有意识地培养学习者的计算思维能力，不但能提高教学效率，还能深入挖掘学习者的潜能，使学习者的信息素养与创新实践能力都有所提高。实际教学过程中还可融入协作学习、案例教学等方法，这些方法和计算思维意识的融合，为大学计算机教学和实践提供了一个方向。