高等数学在工程经济学中的应用

荆州理工职业学院 马 烁

高等数学在工程经济学中的应用

荆州理工职业学院 马 烁

本文侧重研究高等数学在工程经济学中的应用，从高等数学的角度讨论寿命期无限长的互斥型方案的经济评价、非线性盈亏平衡分析和静态模式下设备经济寿命的确定等问题，指出在工程经济学教学过程中善于运用高等数学的有关知识，既可以提高自己的教学水平和学术水平，又能加深学生对本门课程的理解。

高等数学 工程经济学 应用

一、引言

工程经济学是工程经济的理论和方法在工程实践中的具体应用，它以建设工程项目为对象，研究工程技术方案的经济效益，通过计算、分析、比较和评价，以求最佳工程技术方案。数学在工程经济学中扮演着非常重要的角色，工程经济学离开数学寸步难行。因此，教师应苦钻研高等数学知识，这样才能把工程经济学这门课程讲透彻，提高自己的教学水平和学术水平，帮助学生理解这门课程。

工程经济学中涉及大量计算公式，教师在教学过程中不应满足于课本上公式和关系不经推导而直接给定这一现状，应该尽力做到运用学生掌握的高等数学知识去分析并解决问题，进一步加深学生对工程经济学的理解，调动学生学习本门课程的积极性，提高教学效果。

本文从高等数学的角度讨论了寿命期无限长的互斥型方案的评价、非线性盈亏平衡分析和静态模式下设备经济寿命的确定等问题，指出高等数学知识在工程经济学课程教学过程中的重要性。研究数学方法怎样在经济学研究中发挥作用，无疑对于从事经济学研究来说具有重要意义。

二、寿命期无限长的互斥型方案的经济评价

互斥型方案是指在一组方案中选择其中一个方案，排除接受其他方案的可能性，即方案之间具有互相排斥的性质。互斥型方案是工程实践中最常见的，如一栋楼房层数的选择、一座水库坝高的选择、一座建筑物结构类型的选择、一个工程主体结构施工工艺的确定等。这类决策问题常常面对的互斥方案的选择。

通常情况下，各备选方案的计算期都是有限的；但某些特殊工程项目的服务年限或工作状态是无限的，如果维修的足够好，可以认为寿命期无限长，如水坝灌溉、运河及高速公路等工程。对于寿命期无限长的方案，可以计算其资本化成本。所谓资本化成本是指项目在无限长寿命期内等额年费用的折现值，可以用CC表示。设等额年费用（或年净收益）为A，利用高等数学中极限的思想得

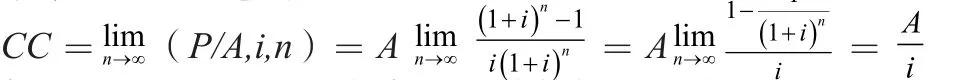
例1：有两个互斥型方案，有关数据见下表，设基准收益率为10%.试求方案可以无限重复下去时的最优方案。

方案 总投资（第0时点）使用寿命（年） 年净收益方案1 7500 4 3800方案2 12000 6 4000

解：分别计算两方案寿命期无限长时的净现值

NPV∞1＝[－7500（A/P，10%，4）＋3800]（P/A，10%，∞)＝14338（万元）

NPV∞1＝[－12000（A/P，10%，6）＋4000]（P/A，10%，∞）＝12448(万元)

因为NPV∞1＞NPV∞2，故方案1为最优方案。

三、非线性盈亏平衡分析

盈亏平衡分析又叫“量本利”分析，是根据项目正常生产年份的产量、成本、售价和税金等因素，确定项目的盈亏平衡点BEP，即盈利为零时的临界值，然后通过BEP（盈亏平衡点）分析项目的成本与收益的平衡关系及项目抗风险能力的一种方法。由于项目的收入与成本都是产量的函数，根据变量之间的函数关系，将盈亏平衡分析分为线性盈亏平衡分析和非线性盈亏平衡分析。现实生活中，生产成本往往与产量不呈线性关系，销售收入和销售价格也会随市场情况而变，与产量不可能一直保持线性函数关系。这时就要进行非线性盈亏平衡分析，一般用二次曲线表示。

设成本C＝a＋bQ＋cQ2，收入S＝dQ＋eQ2，其中a,b,c,d,e为常数，Q为产量。

盈亏平衡时S＝C，即a＋bQ＋cQ2＝dQ＋eQ2

整理得（c－e）Q2＋（b－d）Q＋a＝0

此方程是一元二次方程，可求得两个盈亏平衡点的临界值Q1和Q2，如图所示。

（Q1，Q2）区间称为盈利区，Q＜Q1或Q＞Q2的区间称为亏损区，使S=C取最大值的Qmax就是企业的最优产量。

求Qmax时可以用导数的知识来解决，过程如下：

例2：某项目固定成本是28800元，单位产品变动成本是400元/件，预计项目投产后其产品售价为2000元/件。根据市场预测，每多销售一件产品其售价将降低3元，其单位产品的变动将上升5元。求该项目的盈亏平衡点产量、最大利润点产量。

解：根据题意可知此项目方案是非线性盈亏平衡分析，其收入函数和总成本函数如下：

S＝Q（2000－3Q）

C＝28800＋Q（400－5Q）

盈亏平衡时，S＝C，即8Q2－1600Q＋28800＝0

解方程得，两个盈亏平衡点产量分别为Q1＝20（件），Q2＝180（件）

项目的利润为R＝S－C＝－8Q2＋1600Q－28800

四、静态模式下设备经济寿命的确定

设备的经济寿命是指设备从投入使用开始，到因继续使用在经济上不合理而被更新所经历的时间。它是由维护费用的提高和使用价值的降低决定的。我们称设备从开始使用到其净年值最高（或等值年成本最小）的使用年限N0为设备的经济寿命。即设备的经济寿命就是从经济观点（即收益观点或成本观点）确定的设备更新的最佳时刻。

静态模式下设备经济寿命的确定方法，就是在不考虑资金时间价值的基础上计算设备年平均成本，使设备年平均成本为最小的使用年份就是设备的经济寿命。静态计算法介绍如下：

一般而言，随着设备使用期限的增加，年运营成本每年以某种速度递增，运营成本逐年递增的现象称为设备的劣化。假设每年运营成本的增量均等，每年运营成本增加额为λ，设备使用期限为n年，则第n年时的运营成本为Cn＝C1＋（n－1）λ

式中：C1为运营成本的初始值，即第1年的运营成本；n为设备使用年限。

除运营成本外，在年等额总成本中还包括设备的年等额资产恢复成本，其金额为，则年等额总成本的计算公式为：

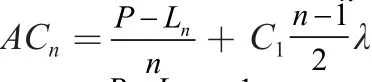
例3：设有一台设备，购置费为8000元，预计净残值为800元，运营成本初始值为600元，年运行成本每年增长300元，求该设备的经济寿。

即该设备的经济寿命为7年。

刚开始讲授工程经济学课程时，由于对这门课的认识不深，很多教师误认为只要将书本上的公式机械地介绍给学生即可。但随着教学过程的展开，发现运用此种方法进行授课，一方面，学生很难理解公式的来龙去脉，造成课程印象不深，很容易忘记，学习效果不明显；另一方面，教师没有深刻研究公式的由来，自己也会感到深深不安。而工程经济学中的许多公式都可以用高等数学的知识推导证明，在后来的教学过程中，尝试运用学生掌握的高等教学知识对有关公式进行推导证明，产生的效果比较明显，学生对工程经济学的认识更加深刻，同时也促进教师教学水平的进一步提高。

本文仅以寿命期无限长的互斥型方案的评价、非线性盈亏平衡分析和静态模式下设备经济寿命的确定等问题为例，实际高等数学在工程经济学中的应用还有很多，限于篇幅，不再一一阐述。

[1]陆海曙.高等数学在技术经济学课程教学中的应用[J].中国科技博览，2009

[2]都沁军.工程经济学[M].大连：大连理工大学出版社，2012

[3]张加瑄.工程技术经济学[M].北京：中国电力出版社，2009

ISSN2095-6711/Z01-2016-12-0238

马烁（1981—），女，汉族，陕西蓝田，硕士，荆州理工职业学院基础课部讲师