一种线性分组码参数的全盲识别算法
王俊霞,张天骐,强幸子,江晓磊
(重庆邮电大学 信号与信息处理重庆市重点实验室,重庆 400065)
一种线性分组码参数的全盲识别算法
王俊霞,张天骐,强幸子,江晓磊
(重庆邮电大学 信号与信息处理重庆市重点实验室,重庆 400065)
提出了一种基于迭代列消元法的线性分组码参数全盲识别算法。该方法首先对截获二进制码流构造截获矩阵,然后对截获矩阵进行迭代列消元法,利用相关列的归一化数目最大值来识别码字长度和同步时刻。同时,对截获矩阵进行迭代列消元法后的矩阵,选取其中一个小矩阵窗内相关列都是全零列,将其对应的转移矩阵中的列向量横向放入校验矩阵,完成校验矩阵的识别。此外,根据相关列和独立列中的码元0的比例减去1的比例的统计特性差异,提出了判别相关列和独立列的门限。仿真结果证明,在误码率为0.01时,该文算法仍能取得很好的效果。
非合作通信;线性分组码;迭代列消元法;相关列
近年来,信道编码盲识别已成为非合作信号处理领域一个新的研究方向,其在智能通信、信息截获和信息对抗领域具有广泛应用[1]。在数字通信系统中,为了提高数据传输的可靠性,通常会采用信道编码技术,通过人为增加冗余比特,使系统具有自动检错或纠错的能力[2]。此外,由于线性分组码具有简单的编码、译码结构和较好的纠错性能[3],因此,在非合作通信中,研究如何根据截获码流识别出线性分组码编码参数具有十分重要的现实意义。
从目前公开发表的文献来看,Planquette G[4]首先提出了利用截获序列构造截获矩阵,根据截获矩阵的秩来识别码字长度和同步时刻的方法,但是利用秩准则识别线性分组码参数,容错率很低。Antoine Valembois[5]首先提出二元线性分组码的检测和识别问题是NP问题,而且利用对偶码空间来识别线性分组码参数,并结合“低码重”思想,该方法有一定的容错能力,但是候选校验向量的数目与假设码长的指数倍数成正比,计算量很大。文献[6]提出了利用walsh-hadamard变换识别线性分组码参数,该方法具有一定的容错能力,但是计算量大,对计算机内存要求很高。文献[7]利用实际码重和随机码重分布的特性不同识别码长,但是该方法仅适用于低码率线性分组码。文献[8]提出了用高斯列消元法识别线性分组码参数,如码字长度、同步时刻,计算量较小,但是容错率有待进一步提高。
针对以上线性分组码盲识别存在的问题,文中提出一种利用迭代列消元法的线性分组码参数盲识别方法,根据相关列的归一化数目来识别码字长度和同步时刻。文中采用迭代列消元法,使错误码元仅仅在窗内传播,对窗外码元没有影响。此外,文中提出根据相关列与独立列中0的比例减去1的比例的概率密度分布的差异,设置门限可区分相关列和独立列,而非传统秩准则中将全零列看作相关列,因此容错率有进一步提高。
1 线性分组码的基础
定义1[9]:将k位信息位分为一组进行独立处理,变为长度为n(n>k)位的编码称为(n,k)线性分组码,码率r=k/n,校验位长n-k。若校验位是信息位的线性组合,则称该编码为(n,k)线性分组码。
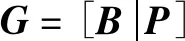
(1)
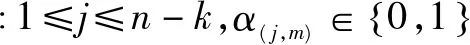
如果将N(N≥k)个码字堆叠成N×n的矩阵,对其高斯列消元法后,相关列可化为全零列,且转移矩阵为
(2)
式(2)右侧区域列向量,即为“相关列”对应的列向量,是n-k个校验向量,并且互不相关,将其横向放入校验矩阵中,此时得到的校验矩阵每一行都与生成矩阵正交。
2 线性分组码参数盲识别原理
2.1 数学模型
假设发送端为(n0,k0)线性分组码,经过二进制对称信道传输,该信道是无记忆、误比特率τ≪1/2的对称信道,且所有码字在发送端等概率发送的,截获二进制比特流为X。非合作方需要估计线性分组码参数,如码字长度、校验矩阵,而且由于截获序列的任意性,需要估计出完整码字的同步时刻d0。
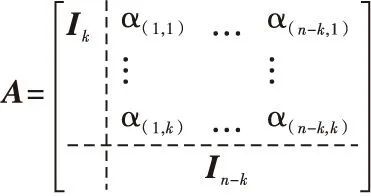
假设该线性分组码的码字长度为n,同步时刻为d,即完整码字起始点为d+1,则截断X前面d比特,以长度为n分成N个码字Xi,i=1,2,…,N,其中,N=⎣(L-d)/n」,⎣」为取整符号,然后将每个码字作为截获矩阵的一行,构成截获矩阵X(n,d),如图1所示,阴影部分表示位于不同完整码字的相同位置的一个比特位。
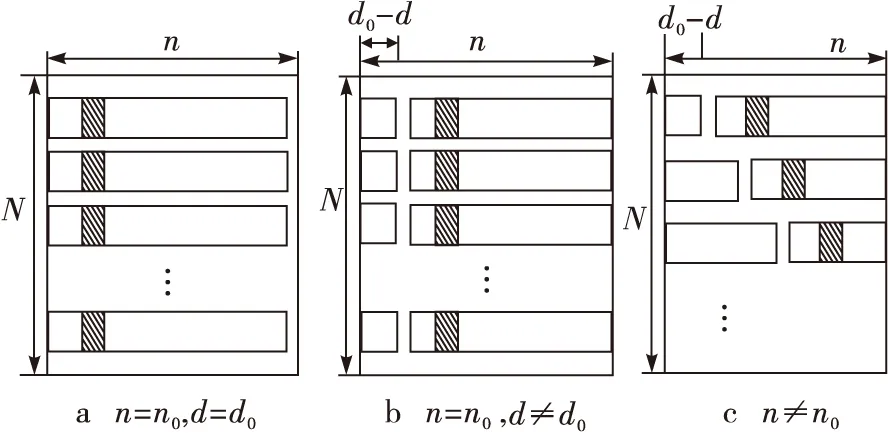
图1 不同码字长度和同步时刻对应的截获矩阵
2.2 迭代列消元法
迭代列消元法的具体流程图如图2所示,迭代列消元法步骤如下:
1) 假设截获矩阵X的大小为N×n的,Xij表示X中第i行、第j列的元素,Xi=(Xi1Xi2…Xin)表示XN×n的第i行,选取小矩阵窗W的大小为m×n,则迭代次数为c=⎣N/m」。
2) 首先将窗W1放置在截获矩阵XN×n的前m行,选取的矩阵记作L(1)=(X1X2…Xm)T,M(1)表示对L(1)进行高斯列消元法之后的行阶梯矩阵,则M(1)=L(1)·A(1),高斯列消元法的结果全部体现在A(1)中。
3) 将窗W1向下滑动m行,窗口记为W2,窗W2内的矩阵为L(2)=(Xm+1Xm+2…X2m)T,同第一次迭代一样将L(2)经过高斯列消元法化为行阶梯形式的矩阵M(2),则M(2)=L(2)A(2)。
4) 依次迭代,每一次迭代都将窗Wi向下滑动m行,并且对窗内矩阵L(t)=(Xm(t-1)+1Xm(t-1)+2…Xmt)Τ进行高斯列消元法化为行阶梯形式,则可以得到M(t)=L(t)A(t),t=1,…,c。
5) 记录迭代列消元法后的矩阵M=(M(1)M(2)…M(c))Τ和转移矩阵A=(A(1)A(2)…A(c))Τ。
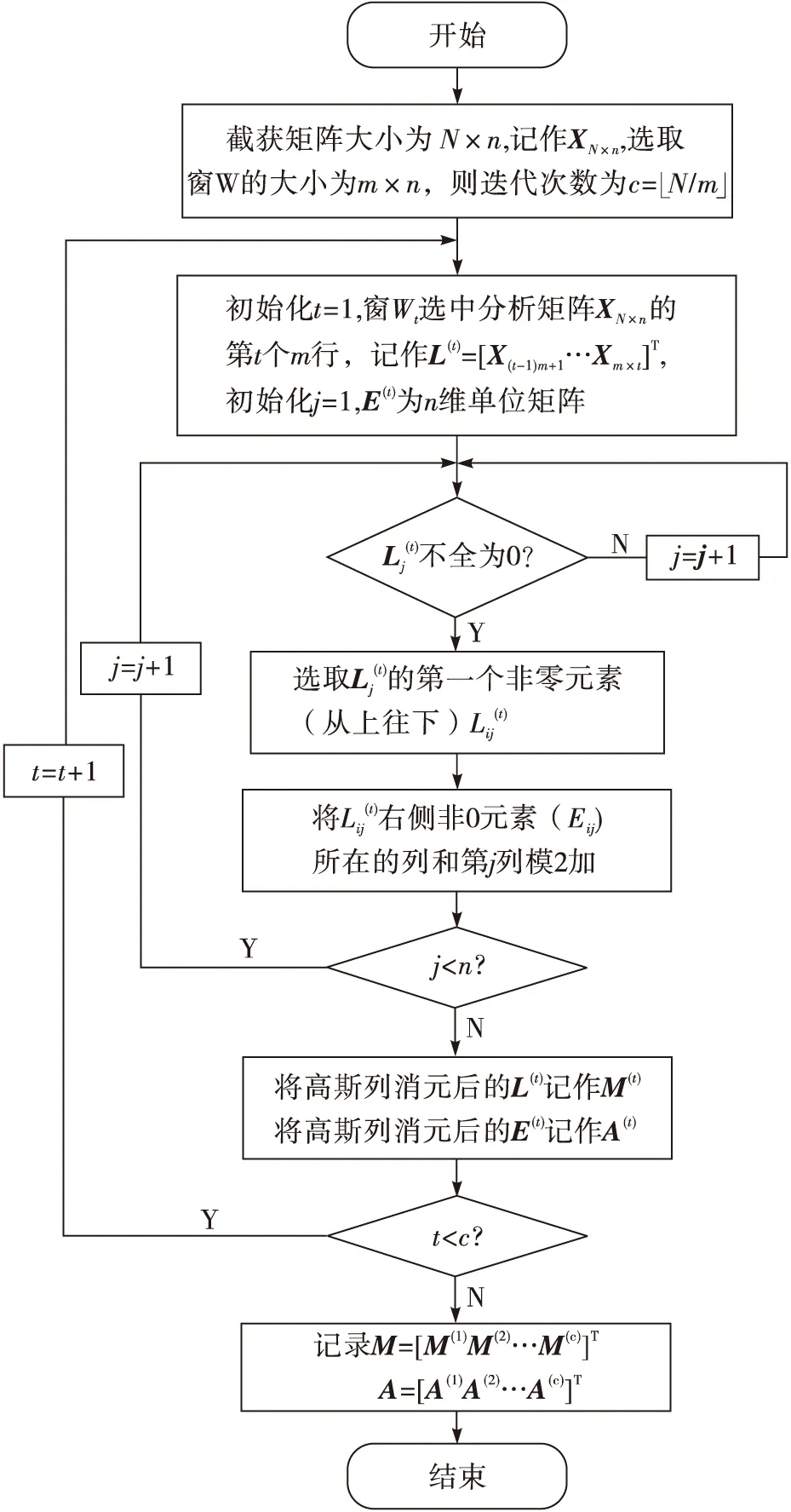
图2 迭代列消元法流程图
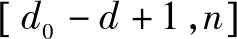
接下来分析在含误码情况下,错误码元对高斯列消元法的影响,以及如何求取相关列的数目。对于含误码矩阵X(n0,d0),当错误码元发生在窗Wi内的前k0行时,则在Wi内的矩阵进行高斯列消元法,会使某一列本不该加的而加到其他列上,或者某一列本该加的而未加到其他列上,此时错误码元的传播范围大,不仅会影响小矩阵窗内相关列的码字重量,而且会影响Wi对应的转移矩阵。但是当错误码元发生在窗Wi内的后2n0-k0行时,仅仅会影响该行对应的相关列的重量[10]。因此,使用迭代列消元法有效地减小了错误码元的传播范围。
文中算法选取窗的大小为2n×n,原因一是滑动窗所选取的矩阵,每一行为一个码字,窗内应该尽量包含k维完整码字;原因二是小矩阵窗的行取值越小,错误码元的影响就越小。
虽然高斯列消元法过程在各个窗内分别进行,但是不同窗内的码字相同位置是上下对齐的。对于无误码截获矩阵,在不同的窗内进行高斯列消元法都可以将相关列化为全零列,且不同的窗对应的转移矩阵都相同。
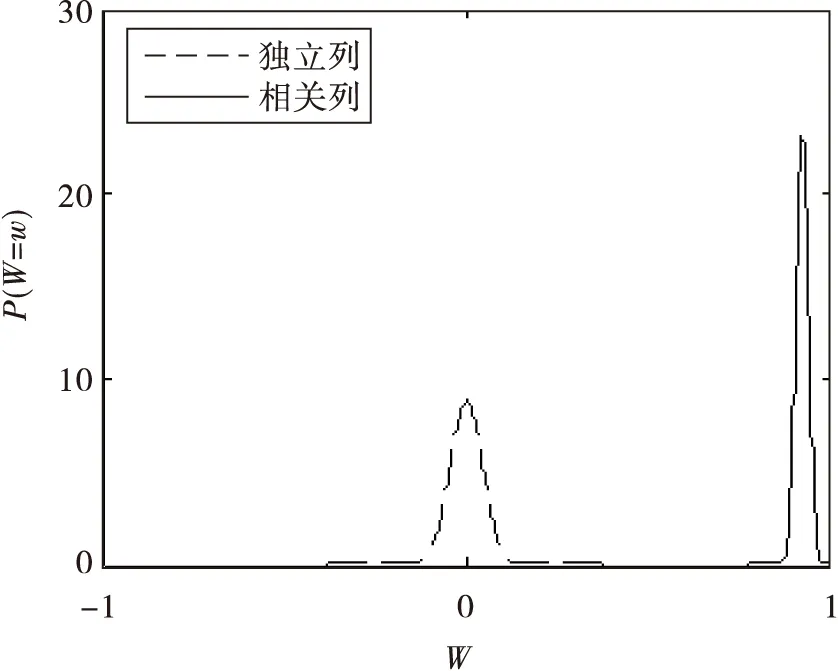
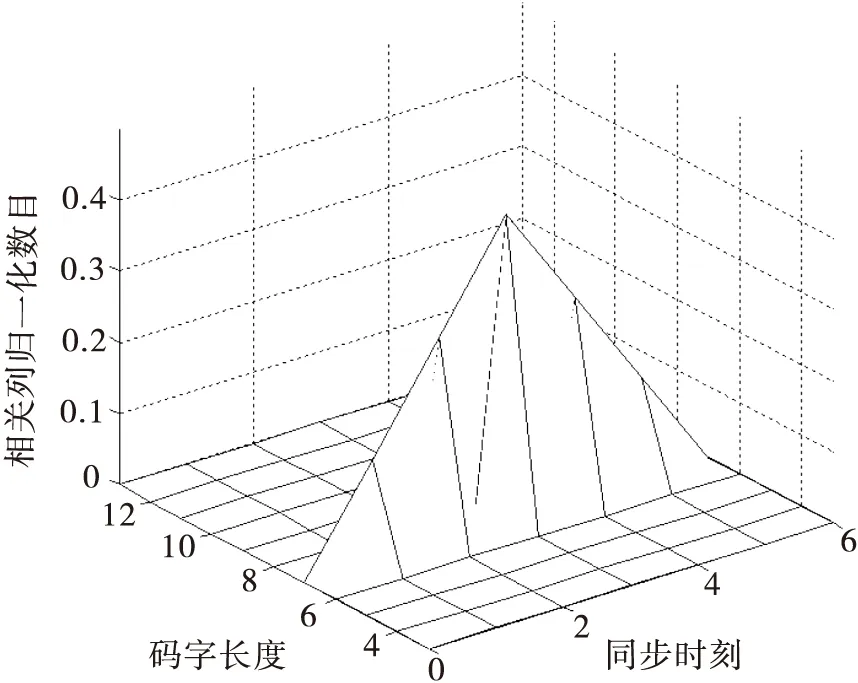
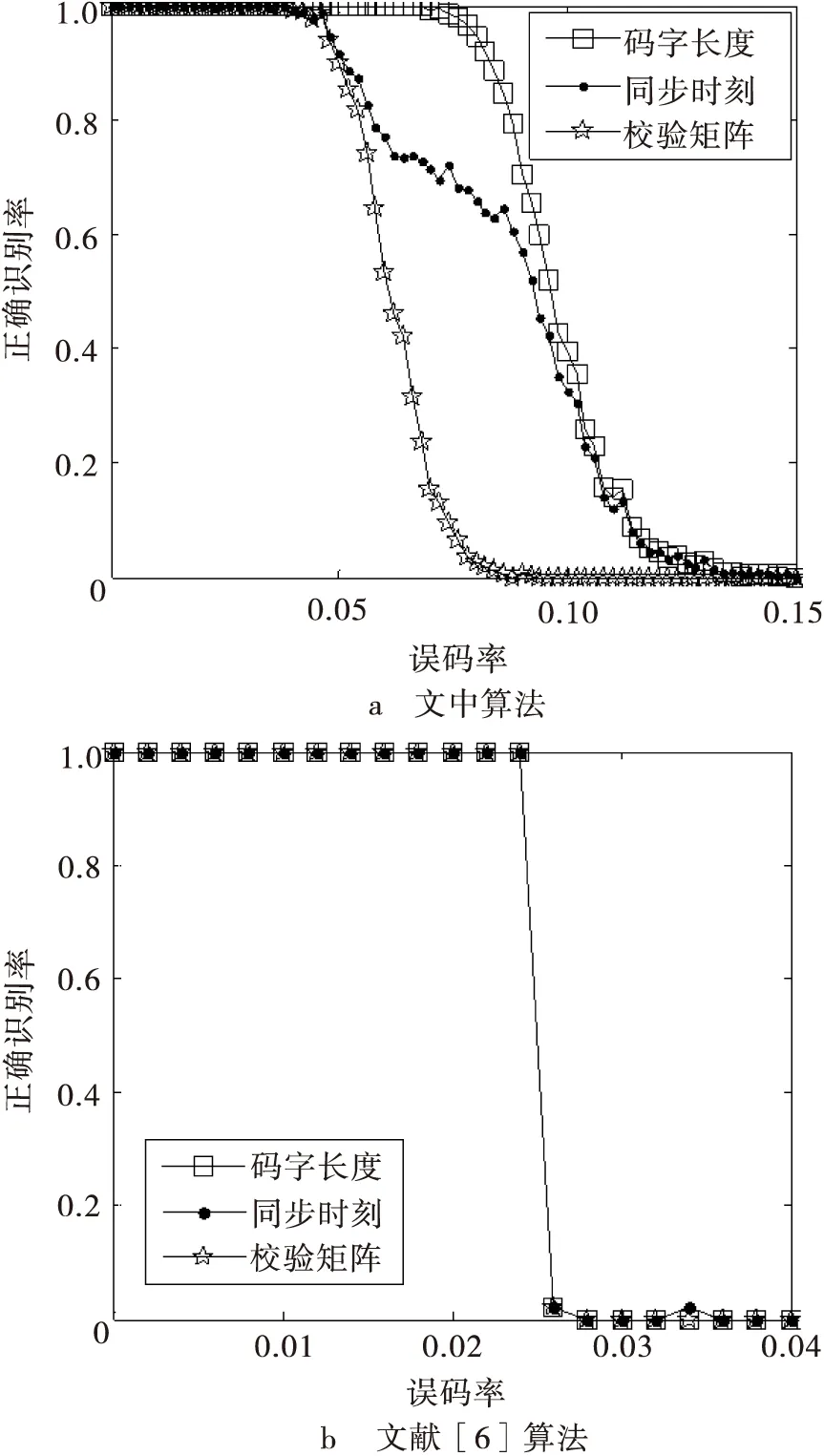
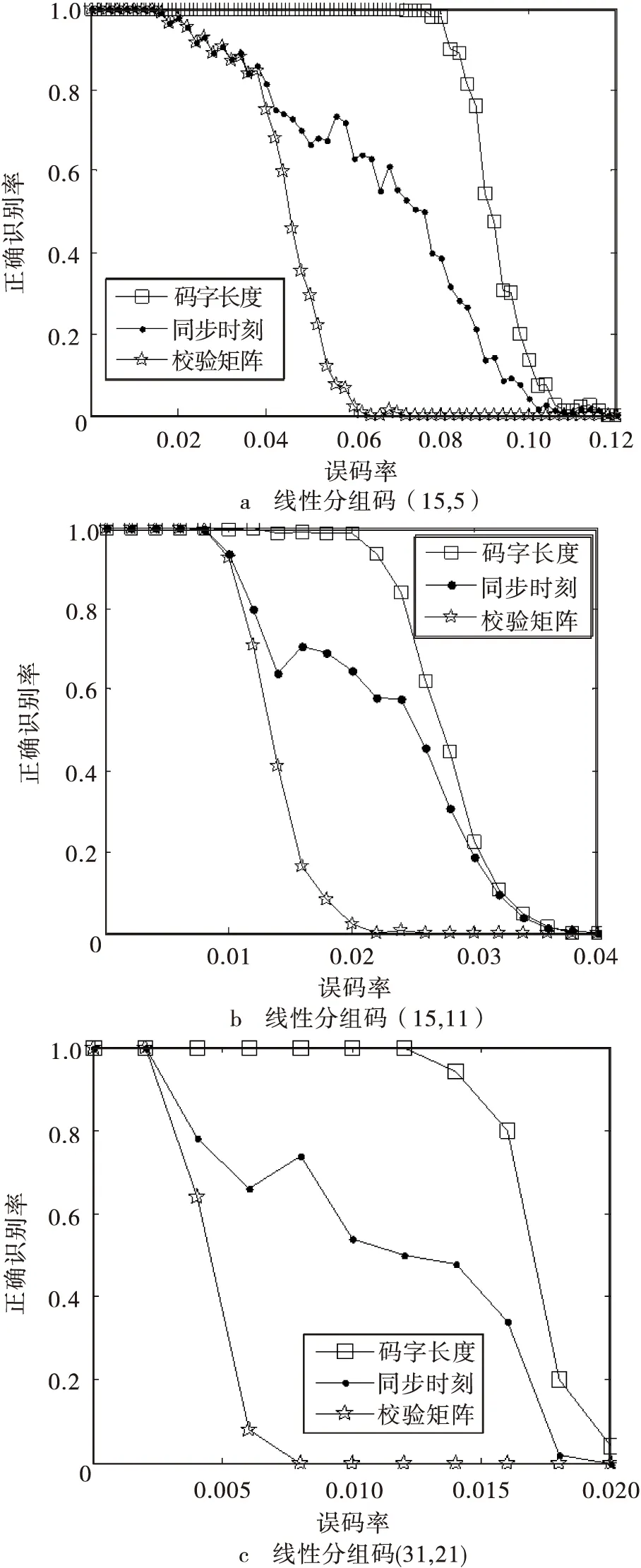
由于对截获矩阵进行迭代列消元法后,会使窗内前k行码元0、码元1受高斯列消元法的影响很大,但是k未知,并且k (3) 若Yj为独立列,则 P(Yij=0)=0.5 (4) P(Yij=1)=0.5 (5) 若Yj为相关列,则 (6) (7) 式中:i=1,2,…,N1;ωt(h)表示校验向量h的重量。 (8) Y中独立列对应的0的比例减去1的比例满足 (9) 如图3所示,取参数值分别为N1=500,τ=0.01,ωt(h)=4时,独立列和相关列对应的0的比例减去1的比例的值的概率密度分布图,设置门限T,如果Wj>T,则认为Yj是相关列,Wj 图3 独立列和相关列对应的W的值的概率分布图 文中算法步骤: 输入:长度为L的截获序列X,选取截获矩阵码长的最小值nmin=3和最大值nmax=2n0-1。 1)初始化n=nmin,d=0; 2) 按照2.1节对以(n,d)构造大小为N×n的截获矩阵X(n,d)=(X1X2…XN)Τ,其中,Xi表示X(n,d)的第i行,对其进行迭代列消元法,可以得到迭代列消元法后的矩阵M=(M(1)M(2)…M(c))Τ和转移矩阵A=(A(1)A(2)…A(c))Τ; 图4 不同码字长度和同步时刻对应的相关列归一化数目 图5 采用文中算法和文献[6]对BCH(7,4)识别的仿真图 图6a是采用文中算法对(15,5)按照误码率从0到0.12,步长为0.002,200次蒙特卡洛仿真结果;图6b是采用文中算法对(15,11)按照误码率从0到0.04,步长为0.002,200次蒙特卡洛仿真结果;图6c是采用文中算法对(31,21)按照误码率从0到0.02,步长为0.002,F50次蒙特卡洛仿真结果。由图6可知,线性分组码(15,5)在误码率为0.04,正确识别率能达到80%,线性分组码(15,11)在误码率为0.01,正确识别率能达到80%,线性分组码(31,21)在误码率为0.003,正确识别率能达到80%。可知,码率越低,识别性能越好,并且文中算法适合各种码率的线性分组码。 图6 采用文中算法对几种线性分组码识别的仿真图 文中对截获矩阵进行迭代列消元法后,根据相关列和独立列对应的0的比例减去1的比例的值的统计特性差异,设置门限,判断出相关列归一化数目,从而识别出正确码字长度和同步时刻。此外,根据迭代列消元法相关列对应的转移矩阵中的列向量为校验向量,所以寻找小矩阵窗内相关列为全零列,认为其不包含误码,选择其对应的校验向量放入校验矩阵中。文中算法在仅仅已知是线性分组码的情况下,可同时识别出码字长度、同步时刻及校验矩阵。 [1] 解辉,黄知涛,王丰华.信道编码盲识别技术研究进展[J].电子学报,2013,41(6):1166-1176. [2] 闫郁翰.信道编码盲识别技术研究[D].西安:西安电子科技大学,2012. [3]FENGGL,TZENGKK.AnewprocedurefordecodingcyclicandBCHcodesuptoactualminimumdistance[J].IEEEtransactionsoninformationtheory,1994, 40(5):1364-1374. [4]PLANQUETTEG.Identificationofbinarycodestreams[D].France:UniversityofRennesI,1996. [5]VALEMBOISA.Detectionandrecognitionofabinarylinearcode[J].DiscreteAppliedMathematics, 2001,111(S1/S2):199-218. [6] 杨晓炜,甘露.基于Walsh-Hadamard变换的线性分组码参数盲估计算法[J].电子与信息学报,2012, 34(7):1642-1646. [7] 王兰勋,佟婧丽,孟祥雅.一种线性分组码参数的盲识别方法[J].电视技术,2014,38(9):188-192. [8] 张世会,张天骐,闫振华,等.BCH码分组交织参数盲识别[J].电视技术,2015,39(15):88-93. [9]LINS,COSTELLODJ.Errorcontrolcoding[M].2nded.NewJersey,USA:PrenticeHall,2005: 67-95. [10]SICOTG,HOUCKES,BARBIERJ.Blinddetectionofinterleaverparameters[J].Signalprocessing,2009,89(4):450-462. 王俊霞(1992— ),女,硕士生,主研信道编码参数的盲识别; 张天骐(1971— ),博士生导师,主研扩频信号的盲处理、神经网络实现以及信号的同步处理; 强幸子(1986— ),硕士生,主研扩频信号的盲处理; 江晓磊(1992— ),女,硕士生,主研导航信号的捕获与跟踪。 责任编辑:薛 京 责任编辑:2016-05-10 Blind recognition algorithm of linear block codes WANG Junxia, ZHANG Tianqi, QIANG Xingzi, JIANG Xiaolei (ChongqingKeyLaboratoryofSignalandInformationProcessing(CQKLS&IP),ChongqingUniversityofPostsandTelecommunications(CQUPT),Chongqing400065,China) In order to solve the blind identification problem of linear block code, an iterative column elimination algorithm is proposed in this paper. First of all, a matrix is filled with intercepted bit stream received from binary symmetric channel, and then an iterative column elimination algorithm is introduced which attempts to eliminate parity bits in codewords of noisy data. Second, the length and synchronization of codewords are estimated when the normalized number of dependent column reaches the maximum. Third, After an iterative column elimination algorithm is applied in the intercepted matrix made of the right length and synchronization, we choose a window whose dependent columns is all zeros column, so the corresponding column in the transition matrix is placed in parity-check matrix. What is more, the threshold is introduced, according to the statistical characteristics differences between dependent column and independent column theoretically. Finally, the simulation results show that the probability of correct recognition in the proposed algorithm is good when the bit error rate is one percent. non-cooperative communication; linear block codes; iterative column elimination algorithm; dependent column 王俊霞,张天骐,强幸子,等.一种线性分组码参数的全盲识别算法[J]. 电视技术,2016,40(12):109-114. WANG J X, ZHANG T Q, QIANG X Z,et al.Blind recognition algorithm of linear block codes[J]. Video engineering,2016,40(12):109-114. TN911.22 A 10.16280/j.videoe.2016.12.021 国家自然科学基金项目(61371164);重庆市市级重点实验室建设项目(CSTC2009CA2003);重庆市杰出青年基金项目(CSTC2011jjjq40002);重庆市教育委员会科研项目(KJ130524);重庆市研究生科研创新项目(CYS14140)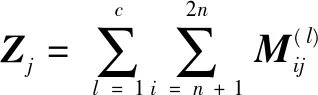
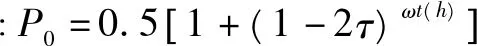
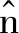
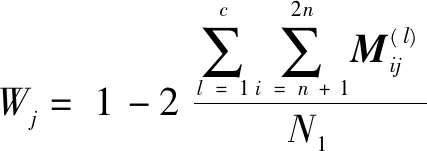
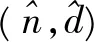
3 仿真验证与分析
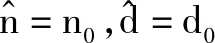
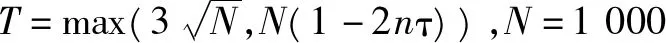
4 小结

