误差函数Chebyshev级数的计算方法

邓国强，唐 敏

(1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004；2.桂林电子科技大学 广西高校数据分析与计算重点实验室，广西 桂林 541004)

误差函数Chebyshev级数的计算方法

邓国强1,2，唐 敏1,2

(1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004；2.桂林电子科技大学 广西高校数据分析与计算重点实验室，广西 桂林 541004)

为了在IEEE浮点计算环境下对误差函数进行精确有效地赋值，提出了误差函数的Chebyshev级数计算方法。采用Clenshaw算法计算级数的前N项部分和，减小求和的舍入误差。实验结果表明，针对误差函数的赋值问题，Chebyshev级数比Taylor级数的收敛速度更快，即达到相同的赋值精度要求时，Chebyshev级数法需要的项数远少于Taylor级数法。

误差函数; Chebyshev级数; Clenshaw算法; IEEE浮点计算标准

特殊函数是一类重要的数学函数，在计算机科学、数学、物理、工程、化学和统计学上都有广泛的应用。通常来说，特殊函数没有一个形式上的定义，但必须是有广泛应用的、满足一些特殊性质的非初等函数，常用的特殊函数有误差函数、Gamma函数、超几何函数、Bessel函数、Airy积分等。因其重要性，许多学者都致力于这些函数的赋值、性质、应用等相关研究。美国国家标准技术研究所(NIST)在2010年出版了NIST数学函数手册[1]，同年发布在线的DLMF(NIST数学函数数字图书馆)[2]，其中包含了大量的特殊函数。

误差函数作为一类重要的特殊函数，对其快速精确的赋值，既涉及到数值计算方法的相关理论，也涉及到浮点计算环境下的具体实现。目前为止，尽管在理论上已经有不少方法可以处理此类函数的计算，但是在当前广泛使用的IEEE浮点计算环境下，由于不同的数值法需要的基本运算操作次数不同，导致舍入误差的大小也相差甚远。一般来说，要达到相同的计算精度，操作次数较少、误差较小的算法更容易被工程上采纳[3]。

误差函数及其互补误差函数在概率、统计和热传导上非常重要，它们是一类热方程的解。对没有初等表达式的特殊函数，其赋值必须采用数值上的近似算法，得到近似解。常用的近似法包括级数展开式、渐近展开式、Pade近似、连分数近似[4-6]等。对于数值算法的选择，在达到要求计算精度的前提下，必须通过有限步的基本算术运算完成。为达到较快的计算速度，需要的操作次数也尽可能地少。为了实现误差函数的快速准确赋值，研究了级数近似求解法，并在IEEE浮点标准环境下[7-8]进行数值实验。通过Taylor级数法和Chebyshev级数法的比较，发现Chebyshev级数法在计算误差函数时，收敛速度远优于Taylor级数法。在达到相同的计算精度要求时，Chebyshev级数法需要的项数要远少于Taylor级数法。为进一步减少舍入误差，在求级数的部分和时采用了Clenshaw算法。

1 误差函数的定义及性质

误差函数erf(x)是一个全函数，定义为

图1为函数erf(x)当自变量在区间[-5,5]的图像。误差函数有对称关系

erf(-x)=-erf(x),

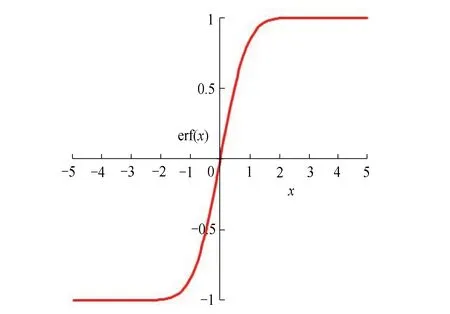
图1 误差函数erf(x)Fig.1 Error function erf(x)

其性质有

erf(x)→1, x→,。

与误差函数erf(x)相关的Dawson积分定义为

实际上，误差函数和Dawson积分是不完全Gamma函数γ(a,x)的特例：

因此，误差函数erf(x)与不完全Gamma函数的关系对推导误差函数的展开式起到了关键作用。误差函数的Taylor级数展开式的推导过程参考文献[6]。本研究关注的是Chebyshev级数在误差函数赋值上的应用。

2 Taylor级数法和Chebyshev级数法

2.1 Taylor级数法

误差函数erf(x)的Taylor级数展开式为

注意到Taylor级数展开式使用的是xk基函数，使用x的幂次作为基函数有其弊端，因为具有x2k形式的函数都具有相同的特性，另一方面，具有x2k+1形式的函数也具有相同的行为。表面来看，基函数是线性相关的。

不使用x的幂次作为基函数，而使用正交基构造多项式，在很多数值计算方法上体现出了优势[3]。Chebyshev级数法正是使用正交基作为基函数的方法。

2.2 Chebyshev级数法

2.2.1 Chebyshev多项式

正交基函数Ti(x)序列满足：

多项式Ti(x)称为Chebyshev多项式，可作为多项式的正交基。Chebyshev级数使用Chebyshev多项式作为基函数，而不采用单项式xi作为基函数[9]。

多项式Ti(x)满足递推关系：

T0(x)=1；

T1(x)=x；

Ti+1(x)=2xTi(x)-Ti-1(x)， i≥1。

图2为前6个Chebyshev多项式的图像。Chebyshev多项式具有很多优良的性质：

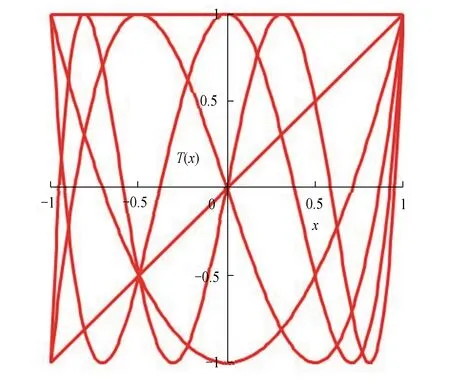
图2 Chebyshev多项式(i=0, 1,…, 5)Fig.2 Chebyshev polynomials(i=0, 1,…, 5)

1) Chebyshev多项式有一个闭式的表达式

Ti(x)=cos(iarccos x)。

3) Ti(x)的零点

每个次数为n的多项式都可用T0(x),T1(x),…,Tn(x)的线性组合表示。以下给出函数f(x)在区间[-1,1]上的Chebyshev级数展开式计算方法，并扩展到任意有定义的区间[a,b]。

2.2.2 Chebyshev级数展开式

若函数f(x)在区间[-1,1]上有定义，且有连续的一阶导数f′(x)，则函数f(x)有一个收敛的Chebyshev级数展开式

Chebyshev级数的系数有闭式的形式，重写式f(x)为

系数τi可由式(1)确定，

(1)

做变量替换x=cos φ，式(1)可转换为

(2)

当没有合适的微积分方法将式(2)转换为实数时，需要采用数值近似法计算系数τi。

当需要求解的函数f(x)是定义在区间[a,b]上时，需要做一个简单的变量替换

，

把区间[-1,1]转换到区间[a,b]上。也就是说，在求解系数τi时，由式(3)确定。

(3)

一旦得到f(x)在区间[-1,1]上的Chebyshev级数展开式，那么计算f(y),y∈[a,b]时，转换为计算

2.2.3 Chebyshev级数的截断误差

若定义在[-1,1]上的Chebyshev级数的系数τi满足

那么对于满足下式的n，

，

截断误差满足关系式：

3 Clenshaw算法

Clenshaw算法(也称Clenshaw求和法)是一种计算Chebyshev多项式的线性组合的递推方法[10]，是计算单项式的线性组合的Horner算法的推广。Clenshaw不仅可运用于Chebyshev多项式，也可应用在任何由三项递推关系定义的函数求和。

3.1 Clewshaw递推公式

Clenshaw递推公式是一种非常巧妙且有效的求和方法。计算模式由一系列系数和其相应的函数相乘，然后对其结果求和。这些函数必须满足一定的递推关系。

假设需要对下式求和

其中Fk满足递推关系

Fk+1(x)=α(k,x)Fk(x)+β(k,x)Fk-1(x)。

α(k,x),β(k,x)是关于k和x的函数。

通过递推关系定义：

把ck当未知数，求解方程(4)，那么

纳入标准：（1）患者肝、肾等功能正常。（2）患者有焦虑症状，SAS评分＞50分。（3）有正常语言表达和理解能力。

注意到式(5)最后一行中β(1,x)被加了一次，又被减了一次。若检查所有含yk的因子，则会发现最终式(5)只剩

f(x)=β(1,x)F0(x)y2+F1(x)y1+F0(x)c0,

(6)

式(4)、(6)就是对f(x)进行求和的Clenshaw递推公式。

因为Chebyshev多项式满足三项递推关系，因此，可以应用Clenshaw算法计算Chebyshev级数的部分和。

3.2 Clenshaw算法求Chebyshev级数部分和

计算Chebyshev级数的前N项部分和

可转化为计算

首先通过Clenshaw算法计算

，

由Chebyshev多项式的递推关系及式(4)，可得

yN+2=yN+1=0，

yk=2xyk+1-yk+2+τk， k=N,N-1,…,1。

对于给定的N和x及计算得到的系数τk。根据上述的递推关系得到y2、y1，然后由

计算出T(x)。

4 数值实验

针对误差函数erf(x)，采用Taylor级数和Chebyshev级数2种近似方法，在IEEE浮点标准计算环境下进行数值实验。实验选择误差函数的自变量区间范围为[0,5]，采样点为1000，均匀分布在整个[0,5]区间上。即采样点坐标为

xi=i/200, i=1,2,…,1000。

第一个实验的目的是测试比较2种级数表示法的近似效果。第二个实验的目的是考查IEEE浮点标准环境下舍入误差对数值计算产生的影响。

4.1 Taylor级数和Chebyshev级数近似计算erf(x)

表1为Chebyshev级数展开式和Taylor级数展开式在项数相同时的平均相对误差。采用的计算精度为10位有效数字。

表1 Chebyshev级数和Taylor级数的比较

从表1可知，随着项数的增加，Chebyshev级数法得到的计算结果的平均相对误差越来越小，在展开到19项时达到了8位有效数字。相比之下，Taylor级数法计算结果的平均相对误差非常大，而且从表1实验的记录来看，项数越多，则误差越大，这是由于Taylor级数在近似计算误差函数时收敛速度非常慢，且数值不稳定。通过进一步的实验可知，若要达到8位有效数字，则Taylor级数需要展开的项数多达73项。表2为Taylor级数法在不同的展开项数时平均相对误差。

表2 Taylor级数法得到的平均相对误差

4.2 舍入误差对计算部分和的影响

在表2中，使用Taylor级数展开式近似计算误差函数，发现从80项增加到100项时，项数的增加并未导致相对误差的减小，其主要原因是IEEE浮点计算环境下舍入误差的影响。从级数的表达式可以看出，求部分和时需要计算的x的多个幂次x2i+1,i=1,2,…,N，项数越多，幂次越高，需要进行的基本运算次数也越多。这样的情况下，舍入误差是一个不能忽略的影响计算结果的因素。

表3是计算精度为10位有效数字和30位有效数字时对计算Taylor级数部分和的影响。从表3可见，在增加中间计算的精度后，近似效果得到大幅度地提升。

表3 舍入误差对计算Taylor级数部分和的影响

4.3 讨论

通过对Taylor级数和Chebyshev级数在近似求解误差函数时平均相对误差的比较，发现Chebyshev级数能在展开项数较少的情况下，获得较高的精度。若需要描绘误差函数的一个粗略的图像，则使用具有2位(及以上)有效数字的近似展开式就可得到较好的效果。图3为N=7时Chebyshev级数展开式得到的区间[-1,1]的图像和高精度计算得到的误差函数在区间[0,5]的图像。从图3可以看出，Chebyshev级数法实际上是将定义域在[0,5]的函数图像平移并压缩到了区间[-1,1]。

图3 Chebyshev级数法图像与高精度erf(x)图像Fig.3 Image by Chebyshev series and high precision image of erf(x)

5 结束语

截断误差和舍入误差是计算一个复杂算术表达式时出现的2种误差来源，对序列的收敛速度进行分析可计算截断误差，舍入误差本质上是因为计算机表示的实数受限于尾数的固定精度，而且计算机硬件只支持有限位机器数的运算，导致舍入误差在计算机中被引入和传播，舍入误差比截断误差更难于分析和控制，计算时必须同时考虑这两种误差。值得一提的是，Chebyshev级数展开式的系数是需要计算积分式的，当项数较多时，会花费相当多的时间求解系数，从而导致计算速度迅速下降。而Taylor级数只需要基本算术运算就能完成，显示了其具有的优势。

[1] OLVER F W J,LOZIER D W,BOISVERT R F,et al.NIST Handbook of Mathematical Functions[M].New York: Cambridge University Press,2010:160-170.

[2] OLVER F W J,LOZIER D W,BOISVERT R F,et al.NIST digital library of mathematical functions[EB/OL].[2016-09-05].http://dlmf.nist.gov/.

[3] HIGHAM N J.Accuracy and Stability of Numerical Algorithms[M]. Philadelphia:Society for Industrial and Applied Mathematics(SIAM),2002:678-698.

[4] OLVER F W J.Asymptotics and Special Functions[M].Wellesley:A K Peters,1997:145-163.

[5] GIL A,SEGURA J,TEMME N M.Numerical Methods for Special Functions[M].Philadelphia:Society for Industrial and Applied Mathematics(SIAM),2007:51-83.

[6] CUYT A,PETERSEN V B,VERDONK B,et al.Handbook of Continued Fractions for Special Functions[M].Birkhauser Boston: Springer,2008:253-259.

[7] Floating-Point Working Group. IEEE standard for binary floating-point arithmetic[J].SIGPLAN,1987,22:9-25.

[8] MULLER J M,BRISEBARRE N,DINECHIN F,et al.Handbook of Floating-Point Arithmetic[M].Birkhauser Boston:Springer,2010:55-58.

[9] MATHEWS J H,FINK K D.Numerical Methods Using Matlab[M].New York:Pearson,2004:365-389.[10] PRESS W H,FLANNERY B P.Numerical Recipes in FORTRAN 77-The Art of Scientific Computing[M].England:Cambridge University,1992:34-45.

编辑：梁王欢

Chebyshev series method for the error function

DENG Guoqiang1,2, TANG Min1,2

(1.School of Mathematics and Computing Science, Guilin University of Electrical Technology, Guilin 541004, China;2.Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation,Guilin University of Electrical Technology, Guilin 541004, China)

In order to evaluate error function efficiently and accurately in the IEEE floating-point arithmetic environment. This paper investigates the Chebyshev series expansion method for the evaluation of the error function. In addition, using Clenshaw algorithm to compute the partial sum of the firstNterms leads to the rounding errors reduction. The experimental results show that Chebyshev series method has faster convergence speed than Taylor series method. In other words, to attain the same computation precision Chebyshev method needs fewer terms than Taylor method.

Error function; Chebyshev series; Clenshaw algorithm; IEEE floating-point arithmetic standard

2016-03-05

国家自然科学基金(11561015)；广西自然科学基金(2016GXNSFFA380009)

唐敏(1980-)，女(壮族)，广西桂林人，讲师，博士研究生，研究方向为高可信计算、浮点计算。E-mail:52121500011@ecnu.cn

邓国强，唐敏.误差函数Chebyshev级数的计算方法[J].桂林电子科技大学学报，2016,36(6)：508-512.

O241.1

A

1673-808X(2016)06-0508-05