不同结构参数下盾构切刀切削土体数值模拟研究

申会宇， 张威威， 张家年

(1. 中铁隧道股份有限公司， 河南 郑州 450003; 2. 盾构及掘进技术国家重点实验室， 河南 郑州 450001；3. 中铁工程装备集团有限公司， 河南 郑州 450016)



不同结构参数下盾构切刀切削土体数值模拟研究

申会宇1,2， 张威威3， 张家年3

(1. 中铁隧道股份有限公司， 河南 郑州 450003; 2. 盾构及掘进技术国家重点实验室， 河南 郑州 450001；3. 中铁工程装备集团有限公司， 河南 郑州 450016)

基于ABAQUS有限元分析软件，采用ALE算法和线性Drucker-Prager土体塑性本构模型，利用具有单元删除功能的剪切失效准则，建立盾构切刀切削土体的三维仿真模型，研究不同切削参数条件下刀具切削土体过程中土屑的流动状态和刀具切削力的变化规律。研究结果表明：在不同的切深状况下，总的切削力变化并不大，但随着切深的增大，已切削土屑的分离度降低甚至不分离；随着刀宽的增大，切削力也随之增大，但土屑的流动性降低；随着前角的增大，切屑的破碎状态和流动性降低，导致堆积在切刀的刀刃处，阻碍切削的持续进行。

盾构切刀； 仿真模拟； 土屑； 切削力； 切深； 刀宽； 前角

0 引言

盾构因具有环保、快速及对周围环境影响较小等优点，被广泛应用于市政、矿山、交通、水工等隧道工程施工中。近年来国内外很多学者利用有限元分析法对盾构切刀与土体之间的相互作用进行了仿真研究，并取得了一定进展[1-4]。文献[5]采用有限元数值仿真分析方法，研究了切刀切土开始阶段和平稳阶段的动态阻力特性；文献[6]采用PMLPG技术，利用计算机仿真，模拟了岩土的切削破碎过程，通过与试验情况相比较，发现两者数值结果较为接近；文献[7]模拟研究桩贯入土体的过程，并预测不同垂直有效应力的内摩擦角；文献[8]提出了一种土层非线性本构模型参数的确定方法；文献[9-10]利用UDEC研究节理特征对滚刀破岩的影响，证明了节理间距和节理倾角对刀具的破岩效率影响很大；文献[11-13]采用有限元法建立盾构切刀切削岩石的三维模型，对切削力和动态过程进行分析，并通过试验验证了模型的合理性；文献[14]利用分析软件Forge3进行隐式有限元计算，模拟三维耕刀的具体切削过程。在模拟材料的硬化和膨胀特性时，引入的非关联法则较为复杂；文献[15-16]采用有限元法建立刀具切削岩石的三维模型，并进行动态模拟和动力学分析。本文从不同角度对盾构切刀做针对性的研究，目的在于通过仿真分析，预测刀体的受力分布状况，讨论切刀在不同前角、切深和刀宽等条件下切削力的变化情况，为刀具的设计和盾构掘进参数的选取提供理论参考。

1 切刀切削仿真有限元模型

为了能够较好地模拟切刀切削土体的过程，对切刀的受力、土屑的流动状态等做出较好地预测，本文参考盾构切刀，运用ABAQUS/CAE前处理程序，建立切刀切削土体的三维实体模型，模型如图1所示。

1.1 土体和切刀的材料参数

对于土体材料，采用Drucker-Prager模型和线弹性模型模拟：在Drucker-Prager模型中设置内摩擦角、膨胀角和流应力比，在Drucker-Prager硬化中定义屈服应力和绝对塑性应变，在剪切损伤中定义土体的断裂应变和破坏位移；在线弹性模型中定义土体的弹性模量、泊松比和密度。土体的具体参数如表1所示。

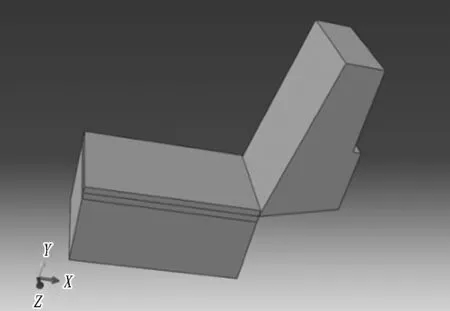
图1 切刀切削土体的三维实体模型

表1 土体参数

切刀在切削土体的过程中，由于土体很软，而且是一个非线性动态过程，所以把切刀设置为刚体，整个仿真过程中切刀不会出现变形，只要对其弹性模量、泊松比和密度等参数进行设置即可，设密度为7 800 kg/m3，弹性模量为210 GPa，泊松比为0.3。

1.2 边界条件

在仿真模型中，把切刀设置为刚体，选定刚体上一点作为参考点，对切刀参考点施加X方向的速度，同时设置刀具沿Y、Z方向的位移约束和X、Y、Z3个方向的转动约束；对于土体模型，底面设置为固定约束，前后两面采用对称约束，上表面和左右2个面设置为自由表面，切刀与土体的边界条件如图2所示。

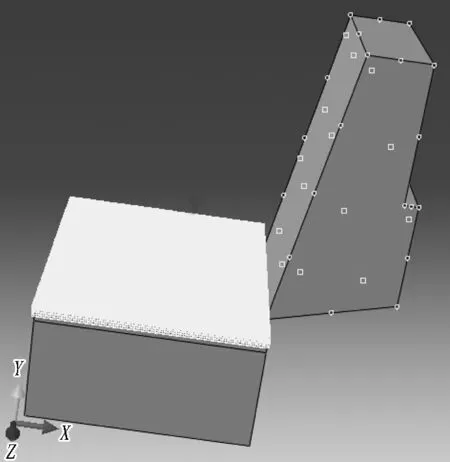
图2 切刀与土体边界条件示意图

Fig. 2 Sketch diagram of boundary conditions of shield cutter and soil

2 盾构切刀切削土体过程的仿真结果与分析

土体切削仿真模拟的目的是为了研究切刀切削土体时土体的塑性变形状态、刀具切削力的变化规律、土体切屑的形成及土屑的流动过程。通过对切刀切削土体的过程进行数值仿真模拟，分析切刀切削力的变化规律，可以间接反映实际施工过程中切刀的受力变化规律。

2.1 切刀切削土体过程的力学分析

在讨论不同前角、切深和刀宽之前，首先就切刀在一个切削过程中不同时刻的受力情况进行分析。本模型土体的三维尺寸为200 mm×100 mm×160 mm，切刀刀宽为120 mm，切深为6 mm。切刀切削土体过程中不同时刻的受力和黏土变形如图3所示，盾构切刀在X、Y方向上的受力变化曲线如图4所示。

从图3可以看出：当切刀不断向前切削时，土体的最大受力区域随着切刀的刀刃向前推进。在整个切削过程中，应力主要分布在切刀与土体的接触区域及土体前端即将被切刀切削的区域，而从土体表面切削下来的土屑应力分布不明显。从数值上可以看出，切刀切削土体的最大Mises应力达到30 kPa，超过黏土的黏聚力，从而使黏土产生剪切破坏。随着切刀对土层的持续切削，切刀对切刀与土体接触的部分施加贯穿力和切削力，综合表现为切削力。当切削力超过土体的抗剪强度时，网格单元开始损伤累计直至失效分离，土体从刀刃与土体接触处发生断裂，形成切屑。此外，由于土体的黏聚力较大，形成流动型切削。从t=0.3 s和t=0.5 s的切削图可以看出，切屑并没有消失，而是随着切刀的不断推进在切刀前表面流动。所以，模拟结果反映了切刀切削土体时切屑的形成和流动过程。

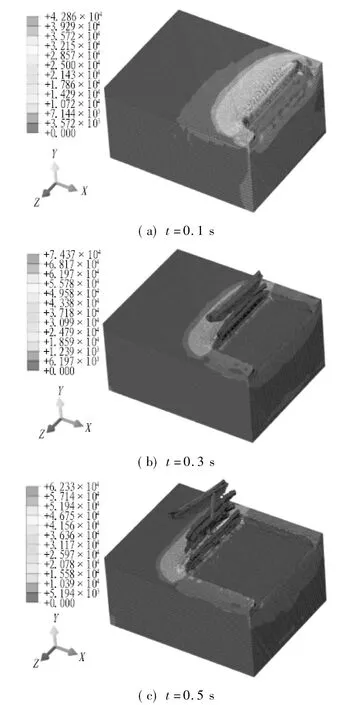
图3 不同时刻土体的等效应力云图(单位：Pa)

Fig. 3 Equivalent stress nephogram of soil at different times (Pa)

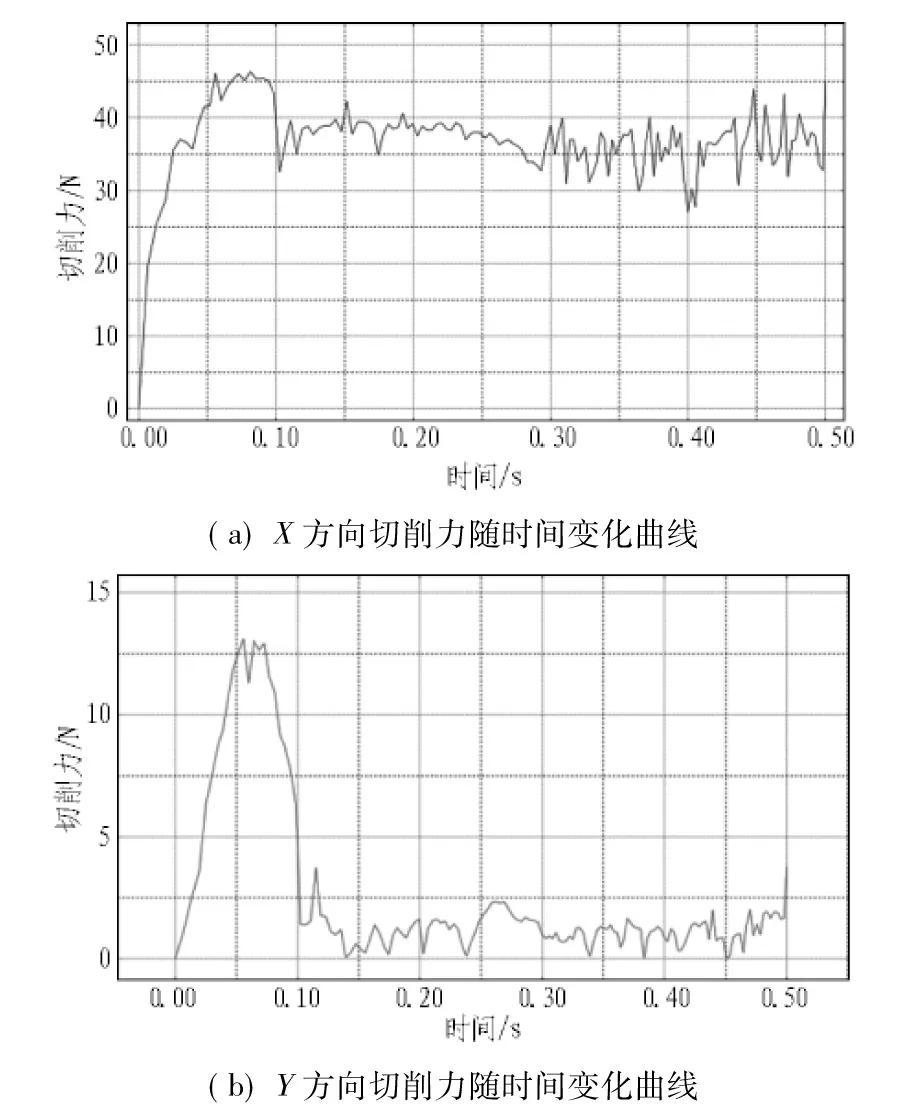
图4 切削力随时间变化曲线图

Fig. 4 Cutting force vs. time

从图4可以看出：切刀刚开始接触土体时，切刀的受力从零骤然增大，这是因为切刀之前的运动相当于空载，即没有任何阻力，当它突然与土体接触时，土体对刀体形成了很大的冲击力，荷载增加，所以受力剧增。随着切刀不断向前运动，切削力趋于平稳，并在一定范围内波动，说明在这段区间内切刀切削趋于稳定。在整个仿真切削模拟过程中，切刀的切削深度始终不变，所以切刀在Y方向上的受力是由刀具和土体之间的摩擦阻力造成的，又由于运用了ALE自适应网格划分技术失效单元及时删除，仿真过程中Y方向的切削力较小。因此，接下来的分析中只讨论X方向上的受力。

2.2 切深对切刀切削力的影响

在盾构实际施工过程中，为了减小切削阻力、延长刀具的使用寿命，应选择合适的切削深度。在切削仿真模拟中，通过设置不同的切削深度来探讨切深对切刀受力的影响。土体模型设置为200 mm×100 mm×120 mm，切刀前角为10°，刀宽为120 mm，切削速度为0.1 m/s，时间为0.5 s，切深d分别取6、8、10 mm。不同切深时X方向切削力随时间变化曲线如图5所示，土体切削效果如图6所示。

图5X方向不同切深时切削力随时间变化曲线图

Fig. 5 Cutting forces alongX-direction vs. time under different cutting depths

图6 不同切深时土体切削效果图(单位：Pa)

Fig. 6 Soil cutting effect under different cutting depths (Pa)

从图5可以看出：在不同的切深状况下，总的切削力并不大。在X方向上，当切深为6 mm时，切削力在20～25 N波动；当切深为8 mm时，切削力在35～40 N波动；当切深为10 mm时，切削力在40～45 N波动。即随着切深的增大，切刀在X方向受到的切削力逐渐增大。

从图6可以看出：当切深为6 mm时，已切削土层的土屑破碎状态较好，沿着切刀前刀面流动；当切深为8 mm时，土屑只是简单的断为两截；当切深增大到10 mm时，已切削土屑并没有分离，在这种状态下持续切削时，容易形成泥饼，增大刀盘的推进阻力和转动扭矩，严重时可导致刀盘停转。所以，虽然不同切深时总的切削阻力并不大，但并不是切深越大越好。

2.3 刀宽对切刀切削力的影响

不同的盾构切刀宽度也会对切刀与土体之间的受力以及土屑的流动状态产生影响，切刀宽度的选择也是影响切刀使用寿命的一个重要因素。土体模型宽度分别设置为80、120、160 mm，切刀前角为10°，后角为15°，切削速度为0.1 m/s，时间为0.5 s，刀宽b分别取80、120、160 mm。不同刀宽时X方向受力曲线如图7所示，土体切削效果如图8所示。

从图7可以看出：随着刀宽的增大，切削力也随着增大。当刀宽为80 mm时，切削力在20～25 N波动；当刀宽为120 mm时，切削力在30～35 N波动；当刀宽为160 mm时，切削力在40～50 N波动。即随着刀宽的增大，切削力逐渐增大，但总体受力并不大，切削力在切刀的使用许可范围内。

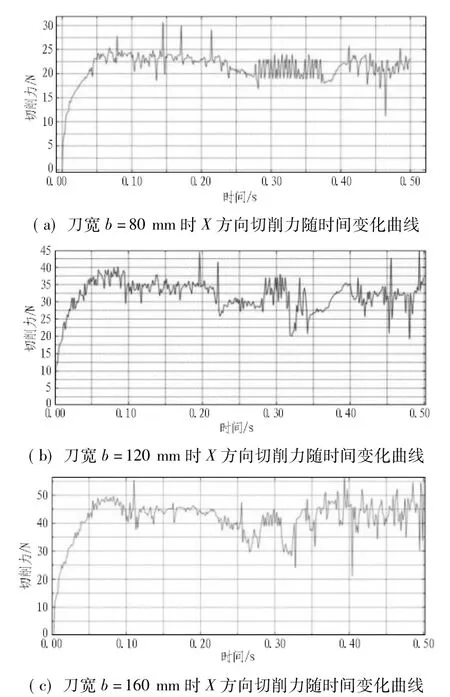
图7X方向不同刀宽时切削力随时间变化曲线图

Fig. 7 Cutting forces alongX-direction vs. time under different cutter widths

从图8可以看出：当刀宽为80 mm时，土屑的破碎状态较好，有利于土屑沿着切刀前刀面流动；随着刀宽的增大，土屑的分离度减小，流动性降低。

综上可以看出：切刀的宽度越小，切刀受力越小，且土屑的破碎状态越好，有利于土屑的流动。但在工程实际施工中，当刀宽设置过小时，对于同一直径的刀盘，就需要安装较多的切刀，此时会增大工程的成本，同时也使刀盘整体变得复杂。所以，实际工程中，在切刀受力许可范围内，根据实际土质状况，可以适当增大切刀的宽度。

2.4 前角对切刀切削力的影响

在实际工程中，切刀前角也会对切刀与土体之间的受力和土屑的流动状态产生影响。通过设置不同的切刀前角来探讨其对切刀受力的影响。土体模型设置为200 mm×100 mm×120 mm，切刀刀宽为120 mm，切削速度为0.1 m/s，时间为0.5 s，切深为6 mm，切刀前角分别取5°、10°和15°。不同切刀前角X方向的受力曲线如图9所示，土体切削效果如图10所示。

图8 不同刀宽时土体切削效果图(单位：Pa)

Fig. 8 Soil cutting effect under different cutter widths (Pa)

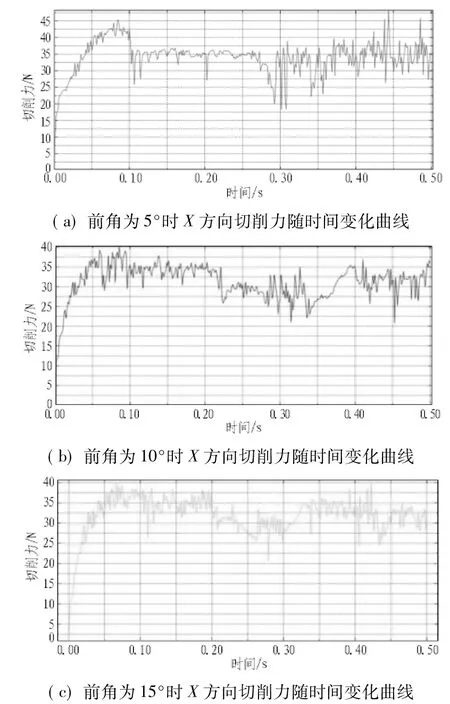
图9X方向不同前角时切削力随时间变化曲线图

Fig. 9 Cutting forces alongX-direction vs. time under different front angles

图10 不同前角时土体切削效果图(单位：Pa)

Fig. 10 Soil cutting effect under different front angles (Pa)

从图9和图10可以看出：随着切刀前角的增大，切刀在X方向的受力呈现减小的趋势，但变化范围很小，总体在30～40 N波动，说明切刀前角对切刀受力影响较小；当切刀前角为5°和10°时，土屑的流动状态较好；当切刀前角增大为15°时，切屑堆积在切刀刀刃处，不能顺畅地沿着切刀前刀面流动，影响切削的持续进行。

综上可以看出：当切刀前角增大时，切刀受力有减小的趋势，但总体变化不大；但随着前角的增大，切屑的破碎状态和流动性降低，导致堆积在切刀的刀刃处，阻碍切削的持续进行。

3 结论与讨论

本文采用ABAQUS有限元分析软件，建立盾构切刀切削土体的三维仿真模型，模拟切刀切削土体的过程，研究切削仿真过程中土体的流动状态和刀具切削力的变化规律，主要得出以下结论。

1)在不同的切深状况下，总的切削力变化并不大，但随着切深的增大，已切削土屑的分离度降低甚至不分离，在这种状态下持续切削时，容易形成泥饼，增大刀盘的推进阻力和转动扭矩，严重时可导致刀盘停转。

2)随着刀宽的增大，切削力也随之增大，但此时土屑的分离度减小，流动性降低。

3)当切刀前角增大时，切刀受力有减小的趋势，但总体变化不大；但随着前角的增大，切屑的破碎状态和流动性降低，导致堆积在切刀的刀刃处，阻碍切削的持续进行。

4)文中仅对单把切刀切削土体进行模拟分析，当2把及多把切刀同时作用时，切削力的变化及土体的流动状态还需进一步研究。

5)文中的侧重点放在了切刀与土体之间的仿真模拟上，在后续的工作中还需要建立切刀切削土体试验平台，通过理论分析和室内试验相结合的手段研究切刀切削土体的过程，为实际盾构掘进提供参考和指导。

[1] 丁峻宏,李根国，金先龙，等. 盾构刀盘切削的三维并行数值模拟[J]. 计算机辅助工程，2006,15(增刊): 303-307.(DING Junhong,LI Genguo,JIN Xianlong,et al.Three-dimensional parallel numerical simulation of cutting by cutterhead in shield machine[J].Computer Aided Engineering,2006,15(S): 303-307.(in Chinese))

[2] Acaroglu O, Ozdemir L, Asbury B. A fuzzy logic model to predict specific energy requirement for TBM performance prediction[J]. Tunnelling and Underground Space Technology,2008,23(5): 600-608.

[3] Abo-Elnor M, Hamilton R, Boyle J T. Simulation of soil-blade interaction for sandy soil using advanced 3D finite element analysis[J]. Soil & Tillage Research,2004,75(1): 61-73.

[4] 费康，张建伟. ABAQUS在岩土工程中的应用[M]. 北京：中国水利水电出版社，2010: 110-120.(FEI Kang,ZHANG Jianwei.Application of ABAQUS to geotechnical engineering[M]. Beijing: China Water & Power Press,2010: 110-120.(in Chinese))

[5] 李守巨，于申，崔娟，等. 盾构机切刀切土过程的有限元模拟分析[J]. 地下空间与工程学报，2013，9(6)：1346-1349.(LI Shouju,YU Shen,CUI Juan,et al. Numerical simulation for breaking soil process of cutting blade on cutterhead of shield machine using finite element analysis[J]. Chinese Journal of Underground Space and Engineering,2013，9(6)：1346-1349.(in Chinese))

[6] 郭峰. 岩土掘削的数值分析新方法与新型装置的研究[D]. 哈尔滨：哈尔滨工业大学，2007.(GUO Feng. Soil dringling & rock cutting’s new numerical analysis method and new equipment study[D]. Harbin: Harbin Institute of Technology,2007.(in Chinese))

[7] Susila E，Hryciw R D. Large displacement FEM modelling of the cone penetration test(CPT) in normally consolidated sand [J]. International Journal for Numerical and Analytical

Methods in Geomechanics,2003,27: 585-602.

[8] 刘增荣，崔伟华，王鑫. 一种土层非线性本构模型参数的确定方法[J]. 地下空间与工程学报，2007,3(8): 225-228.(LIU Zengrong, CUI Weihua, WANG Xin. Parameters determination on nonlinear constitutive model of soil stratum [J]. Chinese Journal of Underground Space and Engineering,2007,3(8): 225-228.(in Chinese))

[9] Hadi B, Reza K, Mohammad A, et al. Simultaneous effects of joint spacing and joint orientation on the penetration rate of a single disc cutter[J]. Mining Science and Technology(China),2011,21(4): 507-512.

[10] GONG Q M,ZHAO J,JIAO Y Y. Numerical modeling of the effects of joint orientation on rock fragmentation by TBM cutters[J]. Tunnelling and Underground Space Technology,2006,21(1): 46-55.

[11] 夏毅敏，薛静，周喜温. 盾构刀具破岩过程及其切削特性[J]. 中南大学学报(自然科学版)，2011,42(4): 954-959.(XIA Yimin, XUE Jing, ZHOU Xiwen. Rock fragmentation process and cutting characteristics on shield cutter[J]. Journal of Central South University(Science and Technology),2011,42(4): 954-959.(in Chinese))

[12] 谭青，徐孜军，夏毅敏,等. 2种切削顺序下TBM刀具破岩机制的数值研究[J]. 中南大学学报(自然科学版)，2012,43(3): 940-947.(TAN Qing，XU Zijun, XIA Yimin,et al. Numerical study of mode of breaking rock by TBM cutter in two cutting orders[J]. Journal of Central South University(Science and Technology),2012,43(3): 940-947.(in Chinese))

[13] 张魁，夏毅敏，徐孜军. 不同围岩及切削顺序对TBM刀具破岩机制的影响[J]. 土木工程学报，2011,44(9): 100-106.(ZHANG Kui，XIA Yimin, XU Zijun. Effects of confining pressure and cutting sequence on the rock-breaking mechanism by TBM cutter[J]. China Civil Engineering Journal,2011,44(9): 100-106.(in Chinese))

[14] Renon N, Montmitonnet P, Laborde P. Numerical formulation for solving soil/tool inter action problem involving large deformation[J]. Engineering Computations,2004,22(1): 87-109.

[15] 李辉，王树林，汪加科. TBM盘形滚刀受力分析[J]. 现代隧道技术，2012,49(3): 193-197.(LI Hui, WANG Shulin, WANG Jiake. Force analysis of the disc cutter on a TBM[J]. Modern Tunnelling Technology,2012,49(3): 193-197.(in Chinese))

[16] 谭青，李建芳，夏毅敏,等. 盘形滚刀破岩过程的数值研究[J]. 岩土力学，2013,34(9): 2707-2714.(TAN Qing, LI Jianfang, XIA Yimin，et al. Numerical research on rock fragmentation process by disc cutter[J]. Rock and Soil Mechanics,2013,34(9): 2707-2714.(in Chinese))

Numerical Study of Soil Cutting by Shield Cutter under Different Structural Parameters

SHEN Huiyu1,2， ZHANG Weiwei3， ZHANG Jianian3

(1.ChinaRailwayTunnelStockCo.,Ltd.,Zhengzhou450003,Henan,China;2.StateKeyLaboratoryofShieldMachineandBoringTechnology,Zhengzhou450001,Henan,China；3.ChinaRailwayEngineeringEquipmentGroupCo.,Ltd.,Zhengzhou450016,Henan,China)

A three-dimensional simulation model of soil cutting by shield cutter is established by means of ALE algorithm, linear Drucker-Prager constitutive model and shear failure criterion with mesh deletion function based on ABAQUS software. The soil flow state and cutting force under different cutting parameters are studied. The study results show that: 1) The cutting force varies a little with the cutting depth varies; and the soil separating rate decreases with the cutting depth increases. 2) The cutting force increases and the soil flowability decreases with the cutter width increases. 3) The soil flowability decreases with the front angle increases.

shield cutter; simulation; soil scrap; cutting force; cutting depth; cutter width; front angle

2015-11-05;

2016-01-26

申会宇(1979—)，男，河南开封人，2003年毕业于郑州大学，自动化专业，本科，工程师，现从事设备技术管理工作。E-mail：29074459@qq.com。

10.3973/j.issn.1672-741X.2016.07.019

U 455

A

1672-741X(2016)07-0881-06