基于不同地形LiDAR点云数据的最优压缩方法
王海君,许捍卫,金文韬
(1.河海大学 地球科学与工程学院,江苏 南京 211100)
基于不同地形LiDAR点云数据的最优压缩方法
王海君1,许捍卫1,金文韬1
(1.河海大学 地球科学与工程学院,江苏 南京 211100)

针对不同地形求解LiDAR点云数据在各种插值算法下不同比例尺允许的标准差内的最佳压缩率,以便提高数据处理的速率,为方便LiDAR数据的处理提供一种简便快捷的压缩方法。介绍了基于ArcGIS软件本源的最佳压缩方法、基于Python的点的坡度差的压缩方法和基于Python的坡度法向压缩方法。
最佳压缩率;地形插值;标准差;坡度差;坡度法向量
本文介绍了基于IDW、NaturalNeighbor、Kriging、Spline地形插值算法下,不同比例尺的LiDAR点云数据的最佳压缩方法[7]。主要运用的是ArcGIS本身的运算方法,同时还介绍基于Python的数据点处坡度差的压缩算法和基于Python的坡度法向压缩算法。本次实验的技术路线如图1所示。
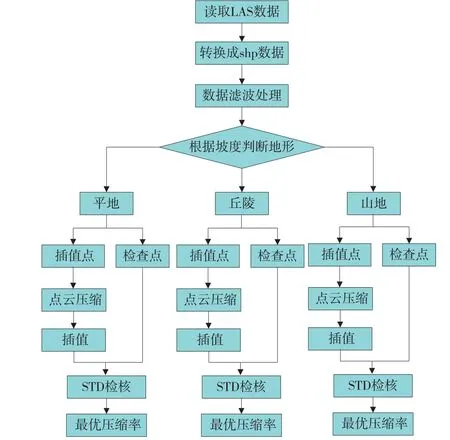
图1 技术路线图
1 数据预处理
由于获取的LiDAR数据是LAS格式,因此需要进行数据转换,可运用自定义数据转换工具将LAS格式数据转换成为shp矢量点数据[9]。
激光扫描仪的工作原理是激光碰到阻碍物时就会返回波,获取的地物高程并不是该地的实际高程,而是该处实际高程与地面植被高之和,直接使用会出现误差,因此需要对数据进行滤波处理[2],减少用此数据构建DEM时对精度产生的影响。
将滤波完成后的shp点数据进行地形分类。此处采用的是按照坡度大小的方式进行分类,通过数据点构建TIN,提取三角面的坡度。根据基于坡度的地形分类标准,地形可分为平地地形、丘陵地形、山地地形、高山地形4大类,每类地形的坡度是不同的,按照坡度进行地形分类的标准如表1所示。
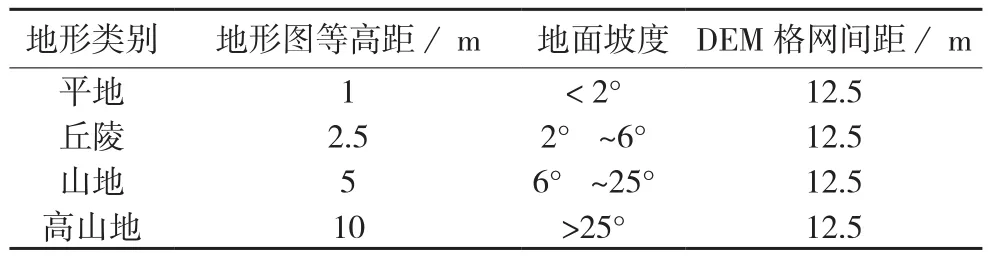
表1 不同地形坡度比较
按照上表将LiDAR点云数据进行分类,分类后的数据分别导出保存,以便后续操作处理。
2 数据压缩及插值分析
根据插值情况的优劣可采用中误差(RMES)或者标准差(STD)来进行检验[5],本文采用标准差(STD)来进行检验,具体标准如表2、3所示。
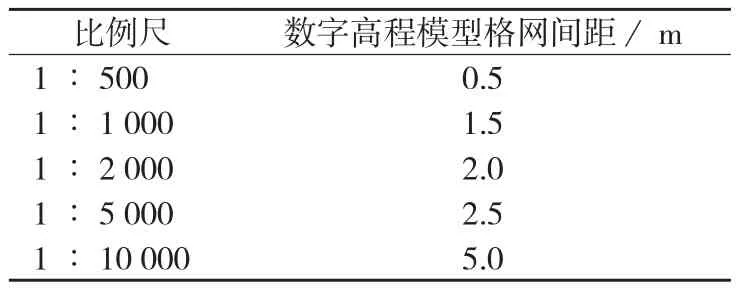
表2 不同比例尺的格网尺寸值
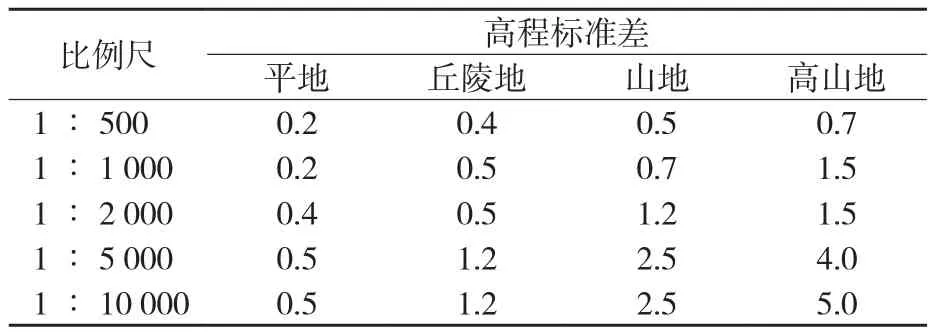
表3 不同比例尺不同地形的高程标准差
2.1 检查点获取
对不同比率的压缩数据插值时,需要对插值结果进行检验,因此需要提前选取检查点。检查点的选取应具有代表性且分布均匀。为了满足这一要求,可以采用标准格网法采点[1],即按照数据的范围划分网格,从每个网格中选取最靠近网格中心点的数据点作为检查点。该方法在保证均匀分布的同时也选择了各种代表类型的点。检查点的选取时还要考虑数量问题,数据点选取太少会出现很大的偶然性,选取太多又会降低存储和操作效率。检查点的选取还要考虑源数据的数量以及该范围内的地形状况,比如相同数据量的平地和丘陵在选取检查点时个数就会不同,明显丘陵地形的检查点数量要大于平地地形的检查点数量。
2.2 数据压缩
2.2.1 基于ArcGIS本源的压缩算法
数据的压缩就是按照需求按比例提取数据点,实现提高操作效率的效果。基于ArcGIS本源的数据压缩方法的具体做法是:①从源数据中剔除检查点,对于插值的检核就是求检查点位置的实际高程与插值后得到的高程的标准差(STD),因此必须事先将检查点处的数据点剔除,以减少真实点数据的影响[7]。可以采用ArcGIS中select by location工具一次性选取检查点并将其删除。特殊地形要保证特征点的存在,如山地的山脊线、山谷线上的点。②构建TIN,将剔除检查点之后的数据构建TIN。③按比例压缩TIN,采用Decimate TIN Node 对构成TIN的结点进行压缩,在设置最大的结点数和容差值时,可根据实际的需求设置参数。④提取TIN Node,提取压缩后TIN的结点,提取后的结点数量大多数情况下与设置的最大结点数量之间存在数量差,实际提取的节点数量小于设置的最大结点数,这些数据将作为插值的数据源。
2.2.2 基于Python的坡度差以及法向压缩算法
1)数据压缩还可以根据该点处构成TIN三角面的坡度差进行压缩[6],具体做法是:①从源数据中剔除检查点;②构建TIN,提取TIN node和TIN triangle;③将node和triangle的Tab表建立special join链接,获得一个点和面的关系表;④求取与点相关联的面的坡度最大值与最小值之差,运用自定义Python程序获取与点相关的面的坡度最大值与最小值,并计算二者的坡度差,将其自动添加到node数据Tab表中;⑤将node数据Tab表中的数据按其坡度差从大到小进行排序,排序后的数据按比例进行数据压缩提取。
基于坡度差的数据压缩方法存在一定弊端,即当数据地形起伏变化快时,选取的点不具有代表性,而且数据的均匀性也不能很好地得到保障,但是当地形变化小时,该方法比基于ArcGIS软件的压缩方法更为有效。
2)数据压缩还可以根据该点处构成的TIN三角面的法向进行压缩,具体做法跟基于坡度差的算法相似,不同点在于基于坡度法向的压缩时根据数据点处各坡面坡度法向的差进行排序后,按照比例选取压缩后的点。
2.3 数据点插值
数据插值主要根据插值方法以及比例尺进行插值变量的设置,主要的做法如下:
1)选择插值方法。选择合适压缩比例的点,在不知道地形情况下可以从50%压缩比例开始,按照选择的比例尺设置参数。不同比例尺的插值做法是相同的,不同点是Output cell size的设置,这个主要根据不同比例尺的格网尺寸值设置。
2)基于检查点位置高程值的提取。数据插值完成后需要提取检查点位置处的插值高程,运用ArcGIS的Extract Multi Values to Points工具提取插值高程,这样在检查点的Tab表中就会出现每个检查点的插值高程。
3)标准差计算(STD)[4]。在检查表中添加new field,运用Field Caculator计算实际高程与插值后所得高程之差,再通过Summary Statistics功能计算二者的标准差(STD)。
4)将所得的标准差与该比例尺下此地形允许的标准差最大值进行对比。若允许值比该值大则选用压缩力度更大的压缩点进行插值比较,反之则选用压缩力度小一点的压缩点进行差值。如此循环直到找到最佳压缩率。
5)换用不同的比例尺或地形重复上述步骤,这样就会得到不同地形不同比例尺不同插值方法下的最佳压缩率。
3 数据检核成果及分析
经过上述插值分析,本次实验以丘陵和平地为例分别根据IDW、NaturalNeighbor、Kriging、Spline算法对数据进行最佳压缩率求解,基于ArcGIS软件的压缩得到的结果见表4、5。
根据以上插值结果可以看出不同的地形压缩率会出现很大的差距,平地在各种比例尺、各种插值方法下的最佳压缩率均远小于丘陵地形。主要原因是平地地形的高程变化小,所以在插值点较少的情况下就可以实现对平地较为精确的插值;而丘陵地形的高程会出现不同程度上的起伏变化,使用少量的点插值会出现标准差(STD)较大的现象。
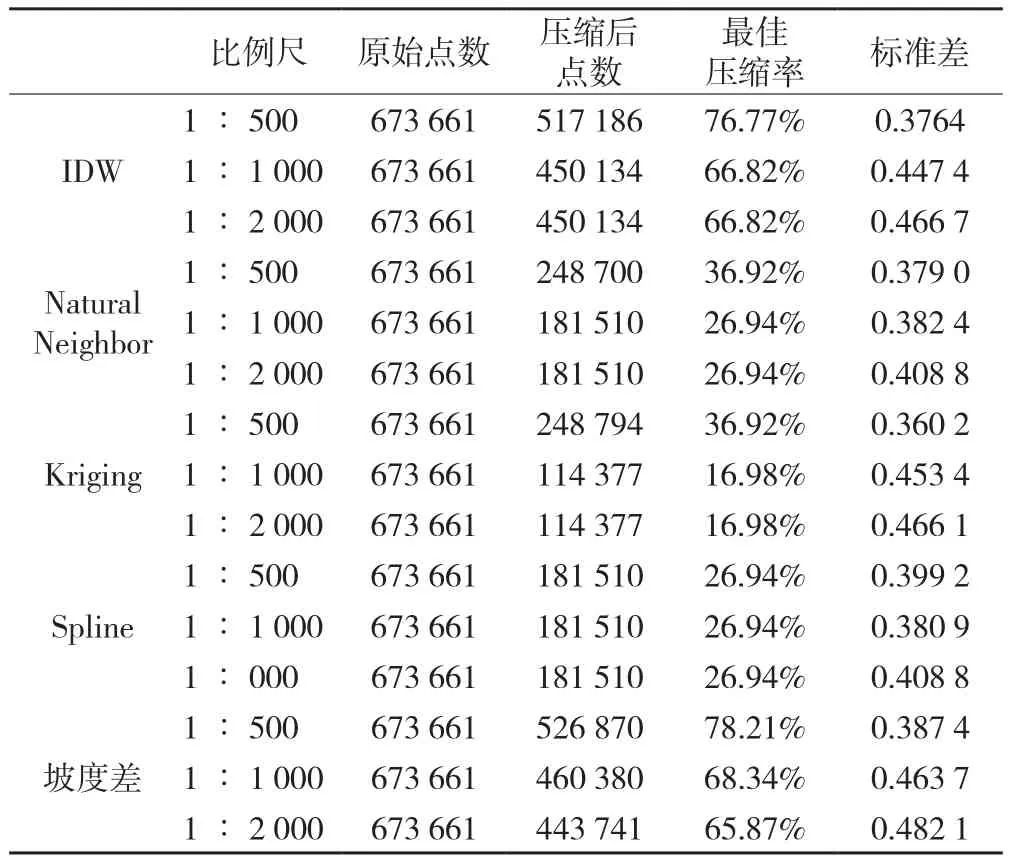
表4 丘陵地形不同比例尺不同插值方法的最佳压缩率
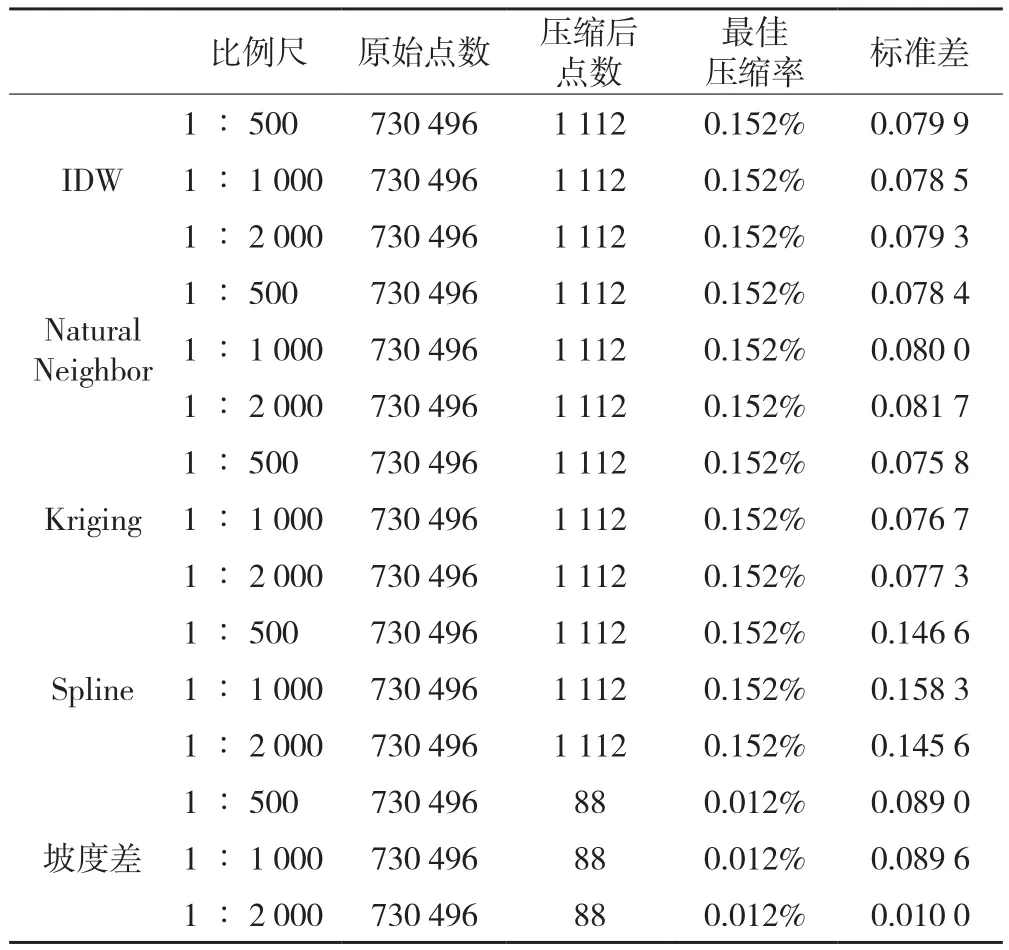
表5 平地地形不同比例尺不同插值方法的最佳压缩率
从丘陵地形的最佳压缩率来看,相同插值算法下在不同比例尺的最优压缩率是有差异的。一般而言,比例尺越大,数据的可压缩性越小,比例尺越小,数据的可压缩性越大。就插值算法而言,NaturalNeighbor算法比较适合丘陵地带的插值。IDW插值方法的压缩率较差,因此IDW方法不适合丘陵地带的插值。
从平地地形的最佳压缩率来看,在各种比例尺和不同的插值方法下最佳压缩率是相同的,主要的原因是当TIN结点压缩达到一定的值之后,就会出现极限结点数,即最佳压缩率。由于平地地形高程变化不大,插值点可以在较少的情况下进行,所以会出现最佳压缩率相同的情况。但从表5中可以看出大多情况下在相同压缩率下比例尺大的标准差相对较小,相同的比例尺下Kriging插值标准差较小,而Spline插值标准差最大,但是都远远小于平地在各比例尺下的最大允许标准差值。
基于坡度差的压缩算法在平地地形的最佳压缩率可以达到0.01%,其效果要优于基于ArcGIS软件本源的压缩方法,但丘陵地形的压缩率IDW插值方法最佳压缩率要在70%左右,其他插值方法的最佳压缩率接近50%,因此在对平坦地形进行压缩时采用基于坡度差的压缩方法效果较为显著,地形起伏较大时采用ArcGIS软件本源算法效果较好。
4 结 语
基于对ArcGIS地形插值的最优压缩方法在不同地形的最佳压缩率有很大差距,平坦地形的最佳压缩率明显优于高程差距较大的丘陵地形;除平地地形外,一般情况下相同地形、同种插值方法下不同比例尺的最佳压缩率是不同的,平地地形在最佳压缩率相同时,不同比例尺的标准差(STD)也不同[3];基于ArcGIS本源的压缩方法下数据点的压缩会达到极限值,之后数据进行更大程度的压缩时,结点的值将不再减少即压缩率不再变化,因此,要根据不同的地形特征选择最为合适的压缩方法。
[1] 刘磊,张建霞,郑作亚. LiDAR点云数据的栅格化重心压缩方法[J].测绘科学,2011,1(1): 90-91
[2] 周梅,邓云凯,张志敏,等.合成孔径雷达数据压缩算法性能分析[J].现代雷达,2009,11(3):44-48
[3] 刘峰,谭畅.机载LiDAR生成DEM的一些关键问题评述[J].中国农学通报,2013,29(1):202-206
[4] 郭宝峰,杨树元.基于样条插值预测的小波图像压缩方法[J].微计算机应用,2000,7(2):194-198
[5] 张宏,温永宁,刘爱利,等.地里信息系统算法基础[M].北京:科学出版社,2006
[6] 刘学军,王叶飞,曹志东,等.基于DEM的坡度坡向误差空间分布特征研究[J].测绘通报,2005,12(1):11-13
[7] 杨玲,刘春,吴杭彬,等.顾及矢量特征的机载LiDAR点云数据压缩方法[J].地理与地理信息科学,2009,25(4):25-27
[8] 王晞.DEM内插算法与精度评定研究[J].现代测绘,2013,9(3): 21-23
[9] 张明希,许捍卫,于艳超,等.基于Python的多波束测深数据压缩研究[J].地理空间信息,2014,4(1):117-119
P231
B
1672-4623(2016)10-0019-03
10.3969/j.issn.1672-4623.2016.10.005
王海君,硕士研究生,主要研究方向为地理信息系统开发与应用。
2015-07-28。
项目来源:国家自然科学基金资助项目(41101374 、41101374);水利部公益性行业科研专项经费资助项目(201201025、201201025)。

