基于罗德里格矩阵的结构变形参数提取方法

余 波，宣 伟

（1.中交第二航务工程勘察设计院有限公司，湖北 武汉 430071；2.武汉大学 测绘学院，湖北 武汉 430079）

基于罗德里格矩阵的结构变形参数提取方法

余 波1，宣 伟2

（1.中交第二航务工程勘察设计院有限公司，湖北 武汉 430071；2.武汉大学 测绘学院，湖北 武汉 430079）

将罗德里格矩阵引入结构体变形参数提取中，首先对全局配准好的点云数据进行结构体特征点的提取，再利用提取的特征点基于罗德里格矩阵进行结构体变化旋转量和平移量的计算，从而实现变形参数的提取。通过对采集的数据进行实验，验证了该方法在结构体变形参数提取中的可行性。

罗德里格矩阵；变形参数；变形提取；结构体

通过对比分析不同切片的变化来获取变形量。以上方法都只是提取变形的大小，没有提取变形的方向。因此，本文将罗德里格矩阵引入结构体变形大小及方向的提取中，通过对全局配准后的点云进行区域匹配，实现变形旋转量和变形平移量的提取。

1 基于罗德里格矩阵的变形参数提取

结构体变形大小及方向提取的关键是进行局部体旋转参数和平移变量的提取，而提取旋转及平移量的方法即罗德里格矩阵法[8]。在进行局部体变形量提取前，需要进行全局配准，而全局配准精度的高低直接影响局部体变形量提取的准确度。所以，为了较精确地提取结构体变形量，本文首先利用ICP算法[9]进行全局配准，再对结构体进行罗德里格矩阵的匹配，从而获得旋转变量和平移变量。

1.1 罗德里格矩阵算法

旋转量和平移量提取的基础是不同期结构体的局部匹配，罗德里格矩阵是进行局部匹配的稳定方法。该方法进行局部匹配的基础是进行反对称矩阵的求取，反对称矩阵表达式为：

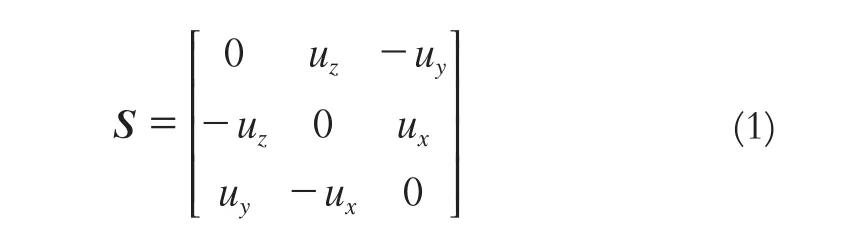
式中，ux、uy、uz相互独立，可由不同坐标系下的坐标分量计算得到。

罗德里格矩阵和反对称矩阵的性质主要有：

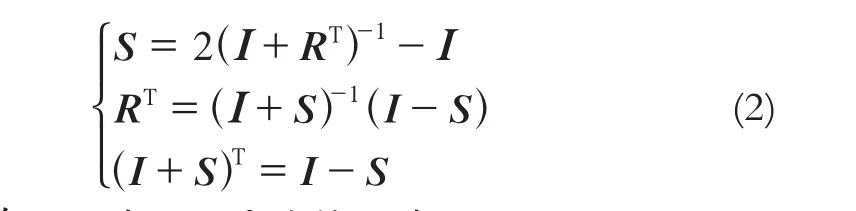
式中，I是单位矩阵；R是旋转矩阵。

根据式（2）便可得到罗德里格矩阵的匹配模型，即匹配模型中的反对称矩阵S必须满足的关系式为：

式中，V0、v0是不同坐标系下同名点的单位向量。

依据式（3）可得反对称矩阵S，再根据式（2）求得旋转矩阵R，而平移矩阵采用不同同名点平移的平均值计算得到。

1.2 结构体变形参数的提取

对某个结构体进行变形前和变形后两次扫描，变形前扫描的点云为（Xi，Yi，Zi），变形后扫描的点云为（xi，yi，zi），将（xi，yi，zi）利用ICP算法进行全局配准，再统一到变形前点云的坐标系中，则变形后的点云变为（Xi'，Yi'，Zi'）；如果此时利用罗德里格矩阵求取变形参数，则该参数是以仪器中心点为基准所发生的变形量。因此，为了得到结构体本身发生的变形量，需要对目标物点云进行归一化处理，即将局部区域点云归一到局部区域的中心，变形前扫描点云归一化处理步骤如式（4）所示。

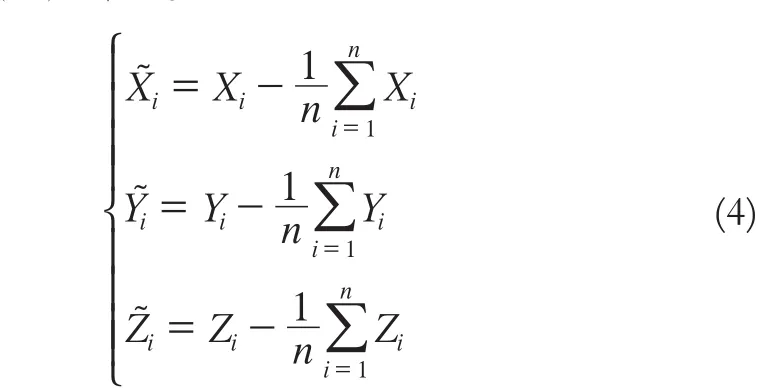
变形后扫描点云数据归一化处理如式（5）所示。

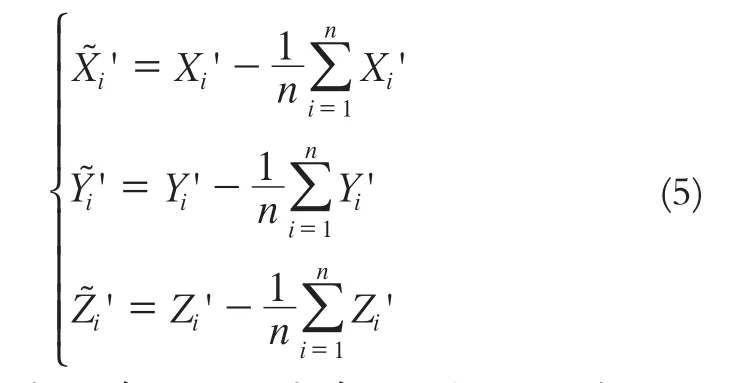
提取变形区域的特征点，将特征点根据罗德里格矩阵算法进行局部区域的匹配，如式（6）所示。

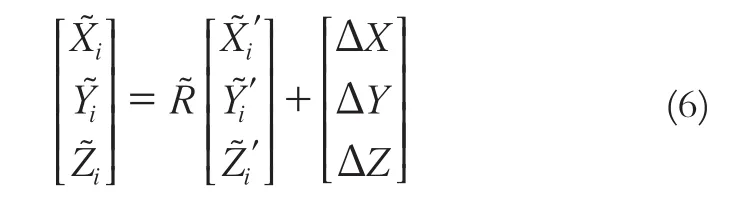
2 模拟实验与结果分析

为了验证本文方法用于结构体变形提取的可行性，利用旋转平台和平移平台对目标物进行旋转和平移的模拟，如图1所示。目标物旋转木板和铝合金材料，采用Riegl-VZ400扫描仪进行扫描，即在目标物旋转和平移前扫描一次，目标物旋转和平移后再扫描一次，将第二次的扫描利用ICP通过全局配准到统一的坐标系统下，再利用罗德里格矩阵进行局部匹配，从而可获取变形的旋转和平移变量。扫描中设置的扫描距离分别为25 m和50 m，扫描过程中设置的采样间隔为2 mm。

图1 模拟目标物的不同变形量

2.1 目标物的平移量提取

首先利用ICP算法将目标物变形后的点云全部配准到变形前的坐标系中，再将点云数据归一到目标物的中心区域，然后选取特征目标物的4个拐点作为特征点，最后利用罗德里格矩阵进行变形参数的提取。为了较精确地获取目标物的特征点，采用区域拟合中心法，即提取目标物4个拐点的区域点云，再对拐点区域点云进行拟合，从而获得拐点中心。实验1利用平移平台模拟目标物的平移量，该平移量模拟的精度为0．02 mm，如图1a所示，模拟的平移量为5 mm和10 mm，通过本文方法提取的平移量如表1所示。

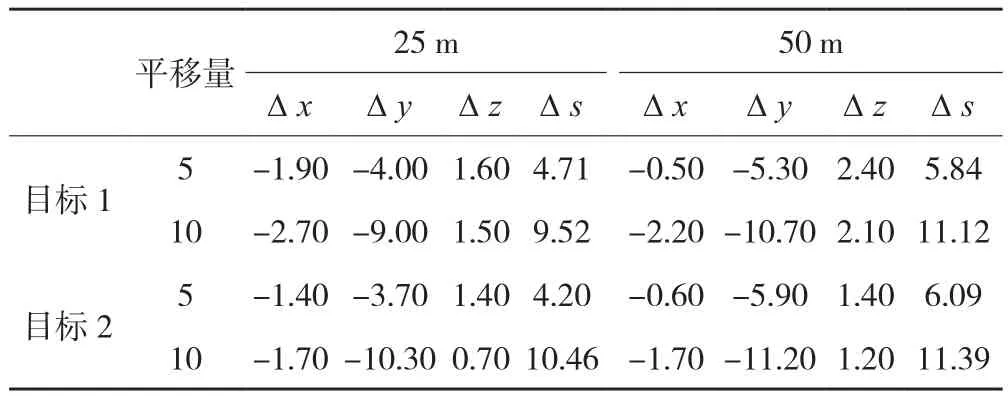
表1 目标物平移提取结果/ mm

由表1可知，25 m的情况下，目标1提取的平移量误差均值为0．4 mm，目标2提取的平移量误差均值为0．6 mm；50 m的情况下，目标1提取的平移量误差均值为1 mm，目标2提取的平移量误差均值为1．2 mm，说明目标1与目标2提取的平移量差值相差很小，不同目标物对平移量提取的影响较小。而25 m情况下提取的目标物平移量误差均值为0．5 mm，50 m情况下提取的目标物平移量误差均值为1．1 mm，后者是前者的两倍左右，即不同距离对平移量提取的影响较大。

2.2 目标物的旋转量提取

实验2利用旋转平台模拟目标物的旋转量，该旋转量模拟的精度为0.05°，如图1b所示，模拟的旋转量为5°和10°，利用罗德里格矩阵进行旋转量的提取，结果如表2所示。

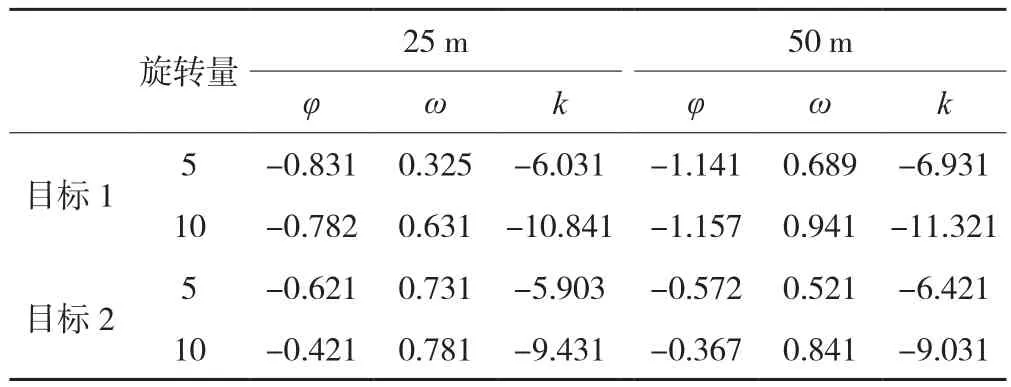
表2 目标物旋转提取结果/°

由表2可知，提取了3个方向的旋转量，而实际模拟的旋转量在一个方向。由图1b可知，在旋转平台整平及正面扫描的情况下，旋转量为k方向的旋转量，将该方向的旋转量提取值与模拟值进行对比分析。25 m的情况下，目标1提取的旋转量误差均值为0.94°，目标2提取的旋转量误差均值为0.74°；50 m的情况下，目标1提取的旋转量误差均值为1.6°，目标2提取的旋转量误差均值为1.2°，说明目标1与目标2提取的旋转量差值相差很小，不同目标物对旋转量提取的影响较小。而25 m情况下提取的目标物旋转量误差均值为0.8°；50 m情况下提取的目标物旋转量误差均值为1.4°，后者是前者的两倍左右，即不同距离对旋转量提取的影响较大。

3 实例分析

利用Riegl-VZ400扫描仪对武汉二七长江大桥进行不间断的扫描，如图2所示，分析车载运动所造成的大桥摆动状况。利用本文方法对桥梁的摆动状况进行分析，提取桥梁顶部的拐点作为特征点，如图2右边圆形框中所示。

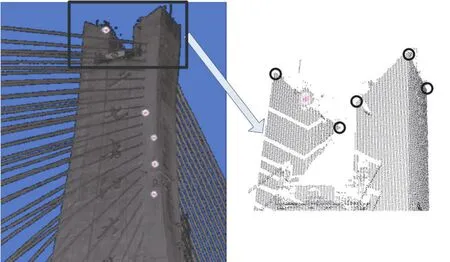
图2 三维激光扫描的影像及点云图

提取图2中的特征点，并利用本文方法进行局部匹配计算，得到桥梁摆动的旋转量和平移量，结果如表3所示。

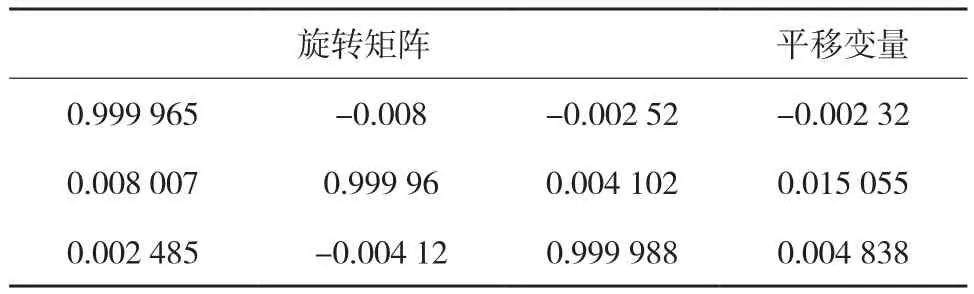
表3 局部匹配结果

根据表3得到局部匹配结果进行摆动旋转量和平移量的计算，结果为：平移量Δx=2.32 mm，Δy=15.05 mm，Δz=4.84 mm；旋转量φ=-0.235°，ω=0.144°，k=0.459°。可知，该桥梁的最大摆动角度为0.459°，最大方向摆动量达到了15 mm，总摆动量为16 mm。而通过全站仪测量的桥梁摆动量为18 mm，即利用三维激光扫描点云数据，基于本文方法得到的变形量与全站仪得到变形量相差2 mm，从而验证了本文方法提取整个结构体变化量的可行性。

4 结 语

本文首先对结构体点云进行归一化，再对归一化后的点云进行特征点提取，然后将提取的特征点引入罗德里格矩阵，实现旋转和平移变量的计算，从而可以较为准确地提取变形参数。提取的变形量不仅有变形大小而且有变形方向，能更准确地反映了整个目标物的变形状况。在提取目标物变形量的过程中，分析了不同距离不同目标物对变形提取的影响，从而避免了特殊目标物对变形提取的影响，使本文方法更加趋近于实际变形分析。

实验结果表明：平移量和旋转量的提取均受扫描距离影响较大，受不同目标物提取影响较小，距离增加一倍，变形量提取的误差增加将近一倍。通过对武汉长江二桥扫描的实例分析，并与全站仪测量数据进行对比，验证了该方法的可行性。本文提出的变形参数提取方法适用于具有结构比较明显的结构体整体变形量的提取，如桥梁、刚体拉杆等整体变形的监测和分析。

[1] 李珵,卢小平,朱宁宁．三维激光扫描隧道断面形变监测精度验证[J]．测绘通报,2013(增刊)∶69-72

[2] 赵小平,闫丽丽,刘文龙．三维激光扫描技术边坡监测研究[J]．测绘科学,2010,35(4)∶25-27

[3] 张国辉．基于三维激光扫描仪的地形变化监测[J]．仪器仪表学报,2006,27(增刊)∶96-97

[4] 王婷婷,靳奉祥,单瑞．基于三维激光扫描技术的曲面变形监测[J]．测绘通报,2011(3)∶4-6

[5] Schäfer T, Weber T, Kyrinovic P, et al． Deformation Measurement Using Terrestrial Laser Scanning at the Hydropower Station of Gabcikovo[C]．Proc． INGEO 2004 and FIG Regional Central and Eastern European Conference on Engineering Surveying, Bratislava,2004∶11-13

[6] Van Gosliga R, Lindenbergh R, Pfeifer N． Deformation Analysis of a Bored Tunnel by Means of Terrestrial Laser Scanning[J]．International Archives of Photogrammetry, Remote Sensing and Spatial Information,2006,36(5)∶5-11

[7] Schneider D． Terrestrial Laser Scanner for Area Based Deformation Analysis of Towers and Water Damns[C]． Proc．3rd IAG Symposium of Geodesy for Geotechnical and Structural Engineering and 12th FIG Symposium on Deformation Measurements, Baden,2006∶22-24

[8] 原玉磊,蒋理兴,刘灵杰．罗德里格矩阵在坐标专注中的应用[J]．测绘科学,2010,35(2)∶178-181

[9] Besl P J, Mckay N D． A Method for Registration of 32d Shapes[J]．IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(2)∶239-256

P258

B

1672-4623（2016）09-0026-03

10.3969/j.issn.1672-4623.2016.09.008三维激光扫描获取的是区域点云，目前国内已将其应用于区域变形提取中，并在实际的工程项目中发挥了重要作用。例如，针对隧道断面的变形，文献[1]利用横断面点云提取进行对比分析，得到的隧道区域变形监测结果达到了mm级；文献[2]首先对三维激光扫描的点云数据进行DEM模型重建，通过新建模型的对比分析确定区域的变形量；文献[3]在DEM模型重构的基础上进行了改进，即不仅分析区域DEM模型的精度，也对变形区域的球形标志进行对比分析，从而获取区域和单点的变形监测结果；文献[4]首先对曲面点云进行拟合，再通过拟合对比分析来确定变形。国外对三维激光扫描的变形监测研究较早，文献[5]通过对比分析点云DEM模型来获取变形量；文献[6]将三维激光扫描技术应用于隧道变形分析，并利用隧道内壁点云拟合参数的变化来获取隧道的挤压变形量；文献[7]对三维激光扫描的电塔点云数据进行切片提取，

余波，硕士，主要从事工程测量、变形监测等相关工作。

2015-05-16。

项目来源：长江科学院开放研究基金资助项目（CKWV2014217/KY）。