二次函数的研究性学习

张继海

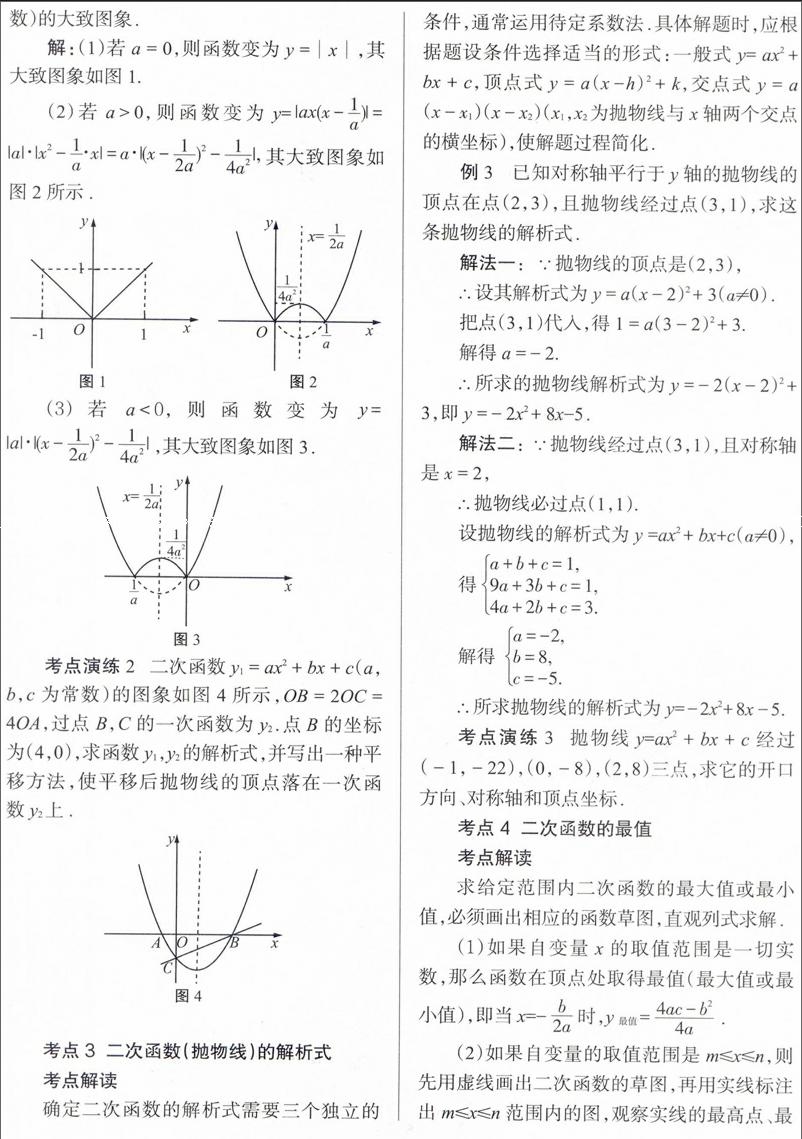
学习和研究二次函数的思路是：实际问题 ? 抽象成概念、规律和性质 ? 理解它们的内涵与外延 ? 概念、规律和性质的应用 ? 演绎变式 ? 同化提高.

二次函数的图象与性质互为依托，相互映衬.在分析和解决二次函数的有关性质时，我们要不由自主地联想或画出其对应的抛物线（即由“数”想“形”），通过抛物线（图形）快速、准确地建立式子，解决问题.反过来，当有“已知，如图（抛物线）”时，我们则需要全方位地对抛物线所反映出来的特征（如开口方向、对称轴、特殊点的坐标、增减性等）进行转化列式（即以“形”助“数”），以求发现最简捷的方法，完美解题.