FRP加固RC梁界面裂缝力学参数有限元分析

邓江东, 孙 卓, 黄海云, 张 波

(广州大学 土木工程学院， 广东 广州 510006)

FRP加固RC梁界面裂缝力学参数有限元分析

邓江东, 孙 卓, 黄海云, 张 波

(广州大学 土木工程学院， 广东 广州 510006)

由于FRP具有高强质轻和施工便捷的特点，粘贴FRP加固钢筋混凝土梁的技术在桥梁工程领域得到了大量的应用，FRP-混凝土之间粘结界面的力学性能是这一技术的关键问题.文章基于ABAQUS的数值模拟，分析FRP加固RC梁界面的开裂，确定界面裂缝的断裂力学参数及关键因素的影响规律，并据此给出了界面裂缝的应变能释放率和应力强度因子的理论表达式，为FRP加固混凝土结构的技术提供技术支持.

钢筋混凝土梁； FRP； 加固； 界面裂缝； 断裂性能参数

纤维增强片材(FRP)在土木工程中大量应用的优势是其高强性能和施工的便捷性，但是FRP与混凝土粘结界面层的有限传力性能常常降低预期的补强效果，导致加固构件界面发生脆性的粘结破坏，其中较为常见的破坏模式是由混凝土弯剪裂缝引起的界面剥离破坏[1-3]，限制了FRP高强性能的充分发挥.目前对FRP增强钢筋混凝土(RC)梁界面性能的研究大多采用材料极限强度理论.由于界面开裂类似于断裂理论中的裂缝，最近一些研究人员也开始把断裂力学的理论应用到FRP加固混凝土结构界面性能的研究中.

ARDUINI等[4]和KO等[5]分别用有限元数值模拟的方法计算了FRP-混凝土界面的应力场.XIE等[6]设计了一种剥离试验研究FRP和基底混凝土的粘结性能，着重分析了FRP剥离角度的影响.

WU,YUAN等[7-8]发现FRP-混凝土界面剥离取决于其开裂能.琚宏昌等[9]则采用J积分方法建立了分析FRP-混凝土界面损伤破坏的模型.

欧阳煜等[10]研究了FRP布加固具有中心穿透裂纹板条在两端拉伸载荷作用下的断裂，推导了FRP 加固板条裂纹尖端的应力强度因子解析表达式.

总体来说目前相关研究还比较少，有鉴如此，本文基于有限元分析软件ABAQUS计算了FRP加固RC梁界面裂缝的应变能释放率和II型应力强度因子，讨论了界面开裂的关键影响因素，并给出了理论计算方法，为FRP加固混凝土结构界面静载破坏和疲劳性能的定量计算提供参考.

1 ABAQUS裂缝模拟方法

应用有限单元法计算裂纹体的断裂参数，单元和节点的布局灵活，裂缝可以任意设置，对各类问题都能得到比较符合实际的解答.

ABAQUS在裂缝模拟方面具有较为先进的算法.ABAQUS主要有3种模拟裂缝的方法：

(1) Smeared cracking，在判断裂缝产生时，采用了塑性屈服面的方法，通过积分点上的主塑性应变矢量图来近似表示裂纹，其大小也只是近似弥散地表示裂纹的宽度.Smeared cracking主要应用于混凝土等材料的计算，显示的裂纹没有明确定量上的意义.

(2) Cohesive elements，用来模拟粘性结点(面)、复合材料的界面层或者其它有具体强度的分界面，计算起裂强度.

(3) Seam，可以准确模拟计算特定裂缝尖端的应力应变场和裂纹扩展方向，计算裂缝的断裂力学参数，本文采用这种方法.

ABAQUS可以直接计算裂缝尖端的J积分，计算简图如图1，J积分的公式：

(1)

式中，Γ为裂缝尖端任一围线；W是裂纹体的应变能密度；T为作用在ds上的应力矢量；u为ds上的位移矢量.

在线弹性的条件下，J积分也就是应变能释放率，J积分和应力强度因子的关系如下：

(2)

E是材料弹性模量；G是剪切模量；KΙ、KΙΙ、KΙΙΙ分别是Ⅰ、Ⅱ和Ⅲ型裂缝的应力强度因子.

在裂缝模拟中ABAQUS默认会直接输出J积分和应力强度因子.

图1 界面裂纹的J积分

2 有限元模型

FRP加固RC梁为平面应力构件，由于对称性，取一半构件建立二维平面模型.

(1)几何模型

有限元模型包括RC梁和FRP 2个部分，如图2所示，RC梁尺寸为0.8 m×0.2 m(长×高)；FRP长度和梁体相同，厚度分别为0.23 mm、0.15 mm和0.30 mm，基准模型中FRP厚度为0.23 mm.

对FRP与混凝土2种材料的连接目前大多采用节点绑定(tie)的方式，但这种方法2节点中间单元边界可能发生脱离和侵入.为了更准确的模拟实际情况，在本模型中把混凝土梁和FRP 2个部分合并成一个整体，2个部分分别设置材料属性，但分析计算中按照一个实体处理，分析过程中裂缝区外的界面节点和单元都共同变形，保证FRP和混凝土完全接触.

图2 FRP加固钢筋混凝土梁有限元模型

Fig.2 FEM model of RC beam strengthened by CFL with interfacial crack

(2)界面裂缝的设定

很多试验证实FRP-混凝土界面剥离破坏主要发生在混凝土一侧，剥离的FRP上会附有一层混凝土，基于试验，有限元模型中界面裂缝位于混凝土中，距离FRP-混凝土界面2.5 mm，裂缝长10 mm，即裂缝尖端距跨中10 mm，沿界面的方向扩展.在ABAQUS中，设定的Seam裂缝面上每个节点上均划分为对应的2个节点，裂缝面可以分开和相互错动.

根据FRP长度方向和混凝土梁网格尺寸1 mm，FRP厚度方向划分3个网格，由于模型网格划分非常密集，未给出单元图.裂缝尖端单元加密，尺寸为0.001 mm，并划分为裂缝计算所需要的环形奇异单元，见图3.

图3 界面裂纹设定

(3)材料属性

计算中设定混凝土和FRP为各向同性的线弹性材料，基准模型中混凝土强度49.4 MPa，弹性模量25 GPa；FRP强度2 900 MPa，弹模240 GPa.为了对比各参数的影响规律，计算中材料性能取值见下文，未标示的参数为基准模型中的取值.

(4)单元类型

混凝土、FRP均采用二次缩减积分单元(Quadratic Reduced-integration element)CPS8R.

二次缩减积分单元计算精度较高，比完全积分单元(full-integration element)在每个方向上减少1个积分点，计算速度更快，但可能存在所谓数值沙漏(Hourglassing)的问题.在ABAQUS中对缩减积分单元引入“虚拟刚度”来抑制数值沙漏，这种方法在正常网格划分时就非常有效，更为精细的单元划分时则完全不会出现这个问题.一般来说，二次缩减积分单元对复杂应力状态和复杂边界条件的模拟计算是低耗时高精度的选择.

3 有限元分析结果

由于FRP很薄，纤维只沿板长度方向布置，因此FRP只能承受沿板长方向的拉力，垂直于板面方向上不能承担弯矩和剪力等荷载.因此，在FRP上施加拉力来模拟界面裂缝区域的受力状态，模型左端施加对称约束.

在基准模型中FRP上施加7.2×108N·m-1的线力，相当于FRP中产生3 000 με的应变，分为5个分析步骤，主要用来计算界面裂缝的应变能释放率G和Ⅱ型应力强度因子KΙΙ.

(1)应变能释放率

有限元模拟计算得到界面裂缝应变能释放率随各参量的变化规律见图4～8.

图4 不同混凝土弹性模量下应变能释放率随FRP应变的变化规律

Fig.4 Change of the energy release rate under different concrete elastic modulus

图4显示界面裂缝应变能释放率不受混凝土弹性模量的影响，3种情况下有限元模拟曲线基本重合，最大值的均值为250.92 N·m-1.

FRP弹性模量取1.2×1010N·m-2、2.4×1010N·m-2和4.8×1010N·m-2时，对应的最大应变能释放率为123.52 N·m-1、250.92 N·m-1和582.61 N·m-1，详见图5；有限元计算数据显示应变能释放率与FRP弹性模量成线性关系，见图6.

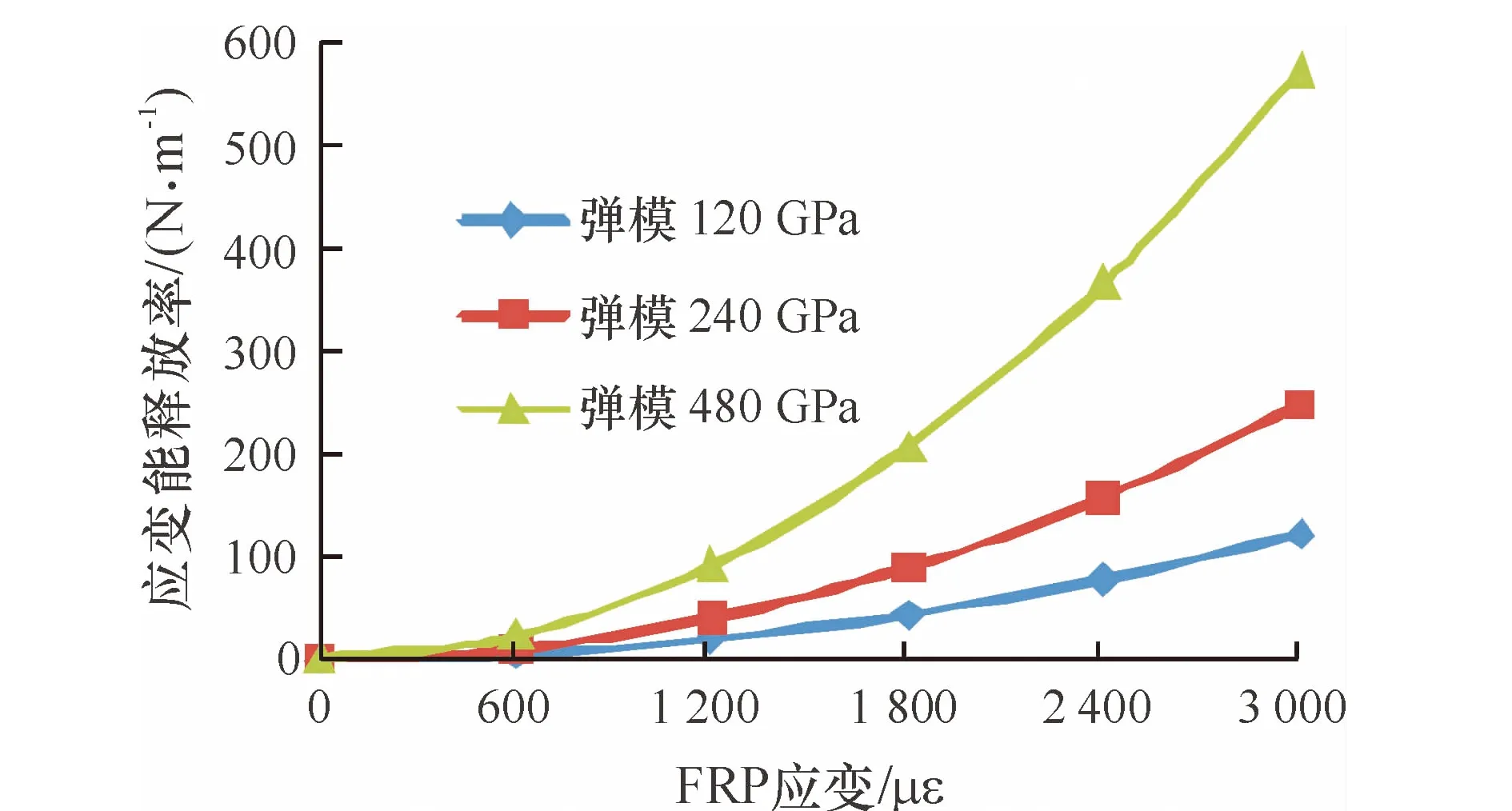
图5 不同FRP弹性模量下应变能释放率随FRP应变的变化规律

Fig.5 Change of the energy release rate under different FRP elastic modulus

图6 FRP弹性模量对应变能释放率的影响

图7显示FRP厚度由1.5×10-4m增加到3.0×10-4m，应变能释放率由144.92 N·m-1增加到364.179 N·m-1.图8显示随着FRP厚度增加，应变能释放率线性增加.

图7 不同FRP厚度下应变能释放率随FRP应变的变化规律

Fig.7 Change of the energy release rate under different FRP thickness

总体来看(图4、图5、图7)，随着FRP应变的增加，界面裂缝的应变能释放率呈二次曲线上升.

图8 FRP厚度对应变能释放率的影响

根据有限元计算的结果和各参数的影响规律，可以得到界面裂缝的应变能释放率为

(3)

式中，K1为参数，根据有限元计算结果K1=0.5，Ef、tf、εf分别表示FRP的弹性模量、厚度和应变.

(2)界面Ⅱ型裂缝应力强度因子

(4)

式中，Ec表示混凝土的弹性模量.

根据有限元的模拟结果，得到界面Ⅱ型裂缝应力强度因子KΙΙ随各参量的变化规律，见图9～图11.

图9 混凝土弹性模量对界面II型裂缝应力强度因子的影响Fig.9 Effect of concrete elastic modulus on the stress intensity factor of model II

图9中数据显示混凝土弹性模量对界面Ⅱ型裂纹应力强度因子的影响.在Ec=25.0 GPa时，应力强度因子有限元计算结果KΙΙ=2 365 780 Pa·m0.5，与理论计算值24 91 987 Pa·m0.5偏差5.1%.在混凝土弹模为12.5 GPa和50.0 GPa时，有限元结果和理论结果的偏差分别为3.9%和5.4%，验证了公式的准确性.

如图10所示，FRP弹性模量分别是120 GPa、240 GPa和480 GPa时，有限元模拟得到的界面裂缝的应力强度因子KΙΙ值为1 644 750 Pa·m0.5、2 365 780 Pa·m0.5和3 787 490 Pa·m0.5，与公式计算值的最大偏差是6.9%.

图10 FRP弹性模量对界面II型裂缝应力强度因子的影响

Fig.10 Effect of FRP elastic modulus on the stress intensity factor of model II

如图11，在FRP厚度为0.3 mm时，界面应力强度因子KΙΙ的有限元计算值为2 888 320 Pa·m0.5，与其理论值2 846 050 Pa·m0.5的差别小于1.5%；FRP厚度0.15 mm时，2者偏差5.3%.

图11 FRP厚度对界面II型裂缝应力强度因子的影响

Fig.11 Effect of FRP thickness on the stress intensity factor of model II

整体来看(图9～图11)，界面Ⅱ型裂缝应力强度因子随着FRP应变的增加呈线性的增长，和式(4)一致.公式计算值和有限元计算值偏差较小.显然减小混凝土弹性模量和FRP抗拉刚度(Eftf)可以减小界面裂缝应力强度因子.在界面裂缝断裂韧性一定的条件下，为了保证FRP能够达到极限应变，就要限制FRP的厚度以保证不会发生过早的界面剥离破坏.

4 结 论

本文对FRP加固RC梁界面裂缝的应变能释放率和应力强度因子进行了有限元数值模拟计算，并且对影响界面断裂的因素进行了分析，可以得到如下结论：

(1)FRP-混凝土界面裂缝的应变能释放率不受混凝土弹性模量的影响，随着FRP的弹性模量和厚度的增加而线性增加，随着FRP应变的增加呈二次方关系增加.

(2)FRP-混凝土界面裂缝应力强度因子与混凝土和FRP弹性模量、FRP厚度的平方根成正比关系，随FRP应变的增加而线性增加.

(3)基于有限元模拟结果给出了界面裂缝应变能释放率和应力强度因子的理论计算公式，这将为研究FRP加固RC梁界面静载和疲劳性能提供定量计算的依据.

[1] SEBASTIAN W M. Significance of midspan debonding failure in FRP-plated concrete beams[J]. J Struct Eng, 2001,127(7): 792-798.

[2] DENG J D, LIU A R, MA Z J, et al. Interfacial behavior of RC beams strengthened with FRP under fatigue loading[J]. Adv Struct Eng, 2015, 18(2): 283-293.

[3] LEUNG C K Y. Delamination failure in concrete beams retrofitted with a bonded plate[J]. J Mater Civ Eng, 2001, 13(2):106-113.

[4] ARDUINI M, DI T A, NANNI A. Brittle failure in FRP plate and sheet bonded beams[J]. ACI Struct J, 1997, 94(4): 363-370.

[5] KO H, SATO Y. Analysis of FRP-strengthened RC members with varied sheet bond stress-slip models[J]. J Adv Concr Tech, 2004, 2(3): 317-326.

[6] XIE M, KARBHARI V. Peel test for characterization of polymer composite/concrete interface[J]. J Compos Mater, 1998, 32(21):1894-1913.

[7] WU Z S, YIN J. Fracturing behaviors of FRP-strengthened concrete structures[J]. Eng Fract Mech, 2003, 70(10):1339-1355.

[8] YUAN H, TENG J G, SERACINO R, et al. Full-range behavior of FRP-to-concrete bonded joints[J]. Eng Struct, 2004, 26(5): 553-565.

[9] 琚宏昌, 张贝宜. 基于线弹性断裂力学的FRP-混凝土界面剥离分析[J]. 郑州大学学报(工学版), 2013, 34(4): 28-31.

JU H C, ZHANG B Y. Debonding analysis between FRP-concrete interface with a linear elastic fracture mechanics approach[J]. J Zhengzhou Univ(Eng Sci Edi), 2013, 34(4): 28-31.

[10]欧阳煜, 卞海涛, 杨峥. FRP布加固具有中心裂纹板条的断裂疲劳性能[J]. 工程力学, 2015, 32(3): 158-166.

OUYANG Y, BIAN H T, YANG Z. Fracture and fatigue behavior of lath with a center crack strengthened with FRP sheet[J]. Eng Mech, 2015, 32(3): 158-166.

【责任编辑： 周 全】

FEM analysis on mechanical parameters of interfacial crack of RC beams strengthened with FRP

DENGJiang-dong,SUNZhuo,HUANGHai-yun,ZHANGBo

(School of Civil Engineering, Guangzhou University, Guangzhou 510006, China)

Since fiber reinforced polymer (FRP) excels in mechanical properties and constructional convenience, the way of bonding FRP to strengthen the reinforced concrete beams has been widely used in bridge engineering. The FRP-concrete bonding interfacial fracture property is a key issue of this technology. Based on the numerical simulation of ABAQUS, the FRP-concrete interfacial fracture was analyzed, and the mechanical parameters of interfacial crack and their key influence factors were determined. Then the theoretical formulas of the strain energy release rate and stress intensity factor for the interfacial crack were given. This paper provides technical support for the technology of concrete structures strengthened with FRP.

RC beams; FRP; strengthening; interfacial crack; fracture parameters

2016-01-21;

2016-03-29

国家自然科学基金资助项目(51308137，51378133);广东省自然科学基金资助项目(2014A030313530)；广州市科技计划项目(201607010094)

邓江东(1979-)，男，副研究员，博士. E-mail：dengjdong@qq.com

1671- 4229(2016)05-0067-05

U 443.22

A