战略性转移定价承诺策略下的供应商选择柔性研究

冯 华，庞 美，刘开军，王天予

(1.武汉大学经济与管理学院，湖北 武汉 430072；2.武汉大学新闻与传播学院，湖北 武汉 430072)



战略性转移定价承诺策略下的供应商选择柔性研究

冯 华1，庞 美1，刘开军1，王天予2

(1.武汉大学经济与管理学院，湖北 武汉 430072；2.武汉大学新闻与传播学院，湖北 武汉 430072)

在上游供应商的战略性转移定价承诺策略与下游制造商投资创新决策之间存在着交互作用，笔者将静态环境下的这种交互作用与不同柔性层次下的动态供应网络架构相结合，以供应链路径柔性为切入点，基于承诺的交货提前期、投资创新、产量与供应链收益等供应链绩效维度来探讨战略性转移定价承诺策略下的供应链合作模式相关话题。考虑到AMj在不同CSi之间进行选择的柔性化特征，笔者至少得到如下三个方面的结论：首先，供应网络架构柔性是供应链整体及其各节点企业获取绩效改善的重要途径，与没有柔性相比，完全柔性和部分柔性情形下的供应链绩效均能得到明显改善，而其中又以完全柔性优势最为突出；其次，虽然部分柔性是供应网络架构中较为可行的柔性层次选择，但是，其与完全柔性一样，容易产生供应网络资源的供给与需求失衡现象；第三，不确定性情境下的一体化决策与确定性情境下的转移定价承诺决策对供应链利润绩效所产生的影响取决于供应网络柔性层次以及供应网络节点企业各自的能力特点，进而对供应链整体及其各节点的合作模式和行为取向起着主导作用。

供应网络；转移定价承诺；供应商选择；柔性层次

1 引言

Radjou[16]指出，全球化运作的制造商必须能够应对“动态化的贸易”。日益激烈的竞争降低了供应链各节点企业的获利空间，从而促进了动态供应链管理理念的发展，在这个前提下，利用供应链柔性来降低供应链提前期、确保生产能力，以及提供多样化的产品以满足顾客的期望受到越来越多的关注[1]。而无论是在战略层面还是在运作层面，高效的供应网络都为供应链应对不同的产品生命周期、根据不同的生产速度转换生产步伐，以及根据对需求的变化预期来选择最适当的供应商或供应商组合提供了更大的柔性[2]。通过识别各个节点企业在流程、信息、创新和关系管理中的贡献，并据之构建高效协同的伙伴关系，动态供应链的价值可以得到极大程度的增值。“满足顾客特定需要的柔性”被看作是一个重要的战略绩效指标[3]。没有柔性(NF)、部分柔性(PF)和完全柔性(MF)是人们在探讨柔性时所普遍使用的术语[3-7]，“柔性化战略”通过整合优化供应链上各节点企业的内外资源，使节点企业及其供应链上的各项业务活动与顾客需求无缝对接，从而对汽车、服装、食品等众多制造供应链企业降低不确定性起到了重要的缓冲机制的作用。例如，上海通用汽车在金桥基地建有中国第一条具有国际先进水平的柔性化生产线，而东风日产则正寻求一场自内而外的转变，提出了“柔性化生产助推‘大格局’”的战略构架……使其既能适应外部市场的变化以迅速满足新产品的加工需求，也表现出了其在出现干扰等不能正常工作情况下的动态调整能力。与这种“柔性化战略”相适应，基于供应网络节点柔性化架构的供应链路径柔性受到了广泛而深入地关注。

如果不存在市场风险，供应商可以通过在转移价格决策中做出承诺来鼓励分销商进行创新投资，但是，如果市场风险很大，这种承诺就需要付出成本。因此，对供应商来说，保留转移价格弹性可以缓解市场风险，但同时也降低了下游分销商进行投资创新的动力，供应商需要在这两者之间权衡利弊。自1980年以来，“速度”成为继“价格”之后又一个重要的竞争要素，如Stalk[8]就指出，新一代的企业大都是“基于时间的竞争者”；Li和Lee[9]，Das[1]也对竞争环境下的市场需求及其企业的价格、质量、技术和交货期等变量进行了探讨；杨文胜和李莉[10]构建了时间敏感需求下的供应链交货期相关定价模型，探讨了供应链的交货期相关定价最优决策策略，基于该模型，冯华等[11]对上游供应商的战略性转移定价承诺策略与下游制造商投资创新决策之间的交互作用进行了探讨，其分析结论可以为基于交货期竞争的供应链企业提供有益指导。不过，现有研究假定外部环境与供应链合作对象既定，针对静态环境下的交互作用进行初步探讨[11]，或者，针对动态环境下的供应网络柔性进行探讨，而忽略了合作伙伴之间的交互决策行为[1, 3, 5-7]。在动态化环境下，当供应网络构造发生变化后，柔性化供应网络架构下的这种交互作用对供应链合作模式及各合作伙伴的行为取向又会产生怎样的影响呢？现有学者在此方面的探讨还非常匮乏！

基于此，笔者从两个层面展开讨论，1)将下游制造商通过投资降低运作成本以提高供应链运作效率作为变量纳入决策模型，其中，上游供应商或者保留转移价格弹性直到下游制造商进行投资创新，或者在下游制造商投资之前就履行转移价格承诺，对上游供应商的战略性转移定价承诺策略与下游制造商投资创新决策之间的交互作用进行探讨；2)进而，将静态环境下的交互作用与不同柔性层次相结合，其中，下游制造商可以在多个提供可替代性资源的上游供应商之间进行非柔性化(只有单一合作供应商)、部分柔性化(有多个在选择权限上有一定限制的合作供应商)和完全柔性化(有多个可供自由选择的合作供应商)决策，基于承诺的交货提前期、投资创新、产量与供应链收益等供应链绩效维度来探讨战略性转移定价承诺策略下的供应商选择柔性相关话题，为供应网络的柔性化架构提供初步的视角。全文共分为四个部分，第一部分是引言，第二部分是战略性转移定价承诺策略模型及其相关文献，第三部分对战略性转移定价承诺策略下的供应商选择柔性进行了界定，并通过示例仿真方法对相应绩效指标进行了仿真分析，最后是结论与研究展望。

2 战略性转移定价承诺策略模型及其相关文献

以一个由单个零部件供应商(CSi(i=1,…,4))和单个装配制造商(AMj(j=1,…,4))组成的供应网络为研究对象，这两个企业按照MTO模式运作，信息完全共享，双方通过转移定价来合作。为简化模型，不妨假设AMj生产一件产品只需CSi提供一个部件，即两节点的产品需求量(假设等于产量)相同，均为yij。对于供应链产品，AMj根据客户需求yij确定产品的最终交货期Tij和价格Pij，并向CSi下订单；CSi根据订单组织生产，并按承诺的交货期Tsij和转移价格tpij向AMj交货；AMj最后进行组装并提交给客户，Tij由CSi承诺的交货期Tsij、其自身的生产/运作流程时间和产品交付运输时间组成。由于大型装配制造商一般采用流水线作业，其生产/运作节拍lmj相对固定，故AMj生产/运作流程时间为lmjyij，同时可假定其交付运输的时间为一常量ldj。这样AMj的交货时间可以表示为：Tij=Tsij+lmjyij+ldj[10-11]。

2.1 交货期-价格敏感性需求

假设客户单位时间的需求量为yij。由于客户需求对于产品的交货期和价格非常敏感，因此期望需求量是承诺的交货期和价格的函数。假设需求是价格和承诺交货期的线性减函数[10]，即yij=ρ-Pij-υTij，其中ρ(ρ≥0)是单位时间内供应链产品的最大需求量，υ是客户单位时间的等待成本[11]。根据假设：Tij=Tsij+lmjyij+ldj，从而有：

Pij=ρ-υ(ldj+Tsij)-yij(1+υlmj)

(1)

由于生产和物流过程中存在着不确定性，笔者假设CSi的实际交货期ti是一个均值为1/λi,(λi>0)的服从渐近指数分布的随机变量[12]，其密度函数为f(ti)，分布函数为F(ti)：

F(ti)=1-e-λiti,(λi>0)。

2.2 模型及符号定义

假设AMj通过投资M(θij)将其成本从Cmj降低到θijCmj，其中0≤θij1，M′(0)=-∞，M(1)=0，M′(1)=0。对于投资函数，Porteus[13]和Cho和Gerchak[14]曾考虑了对数函数和指数函数，以其研究为依据，笔者令M(θij)=Ij(1-θij)2，θij越低表明运作效率越高，创新投资力度越强；而θij<1则可以保证AMj有一部分成本是不可控制的；Ij是AMj可以提供的最大投资额，是一个正常数。即通过投资Ij(1-θij)2，AMj可以将其变动成本降低(1-θij)Cmj。

一般而言，CSi的短期成本结构包括三个组成部分：(1)生产成本，包括与生产相关的直接材料、劳动力和在制品成本等；(2)库存成本，由于在交货期之前完成订单而产生的相关库存成本；(3)延期惩罚成本，由于未能在交货期之前完成订单而产生的赶工成本或延期惩罚成本。假设CSi的目标是使其单位时间内的期望收益(πsij)最大化[15]：

πsij(tpij,Tsij)=[tpij-Csi-αiG1i-βiG2i]yij

(2)

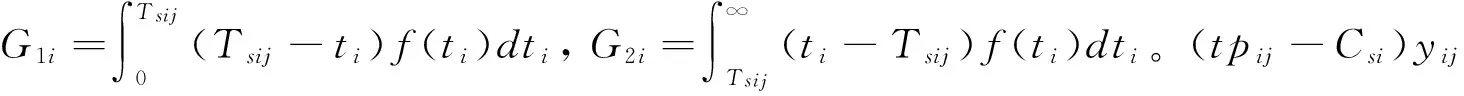
同样，假设AMj的短期成本结构包括三个部分：(1)从CSi购买产品的转移支付；(2)生产成本；(3)缺货成本，即CSi延期交货而产生的成本，该成本与缺货数量成正比，单位产品单位时间内的缺货成本是一个常量。AMj的目标是使其单位时间内的期望收益(πmij)最大化：

πmij(tpij,Tsij)=[ρ-υ(ldj+Tsij)-(1+υlmj)yij-tpij-θijCmj-δjG2i]yij-Ij(1-θij)2

(3)

在AMj的目标函数中，[ρ-υ(ldj+Tsij)-(1+υlmj)yij-θijCmj]yij是期望收益，Cmj是单位变动成

2.3 战略性转移定价承诺模型

假设CSi和AMj拥有相同的信息，且能在完全地转移定价弹性与完全地转移定价承诺策略之间进行充分地权衡。这样，就形成了存在于CSi的战略性转移定价承诺与AMj投资决策之间的交互作用：1)FF(CSi保留转移定价弹性，AMj保留生产量决策弹性)；2)CF(CSi提供转移定价承诺，AMj保留生产量决策弹性)；3)CO(CSi提供转移价格和交货期双重承诺)；4)IW(CSi交货期不确定前提下的一体化供应链)；5)IO(CSi交货期确知前提下的一体化供应链)。不同的交互作用直接影响到CSi最优的承诺交货期和AMj的最优创新投资决策(见表1)。

3 战略性转移定价承诺策略下的供应商选择柔性

在网络架构既定的供应链合作中，根据合作双方所处的主从地位以及各自对最优决策变量的侧重点不同，上游供应商CSi与下游制造商AMj可以分别通过战略性转移定价承诺、交货提前期决策和生产量、创新投资决策之间的交互作用来为自己争取尽可能最优的合作模式。

表1 战略性转移定价承诺策略下的供应链绩效一览表[11]

注：Fij=ρ-υldj-Csi-Cmj，Kij=-[υ+λi(Csi+Cmj+νldj-ρ)+K2ilnK1ij/K2i]，K1ij=αi+βi+δj，K2i=υ+αi，K3j=1+υlmj。

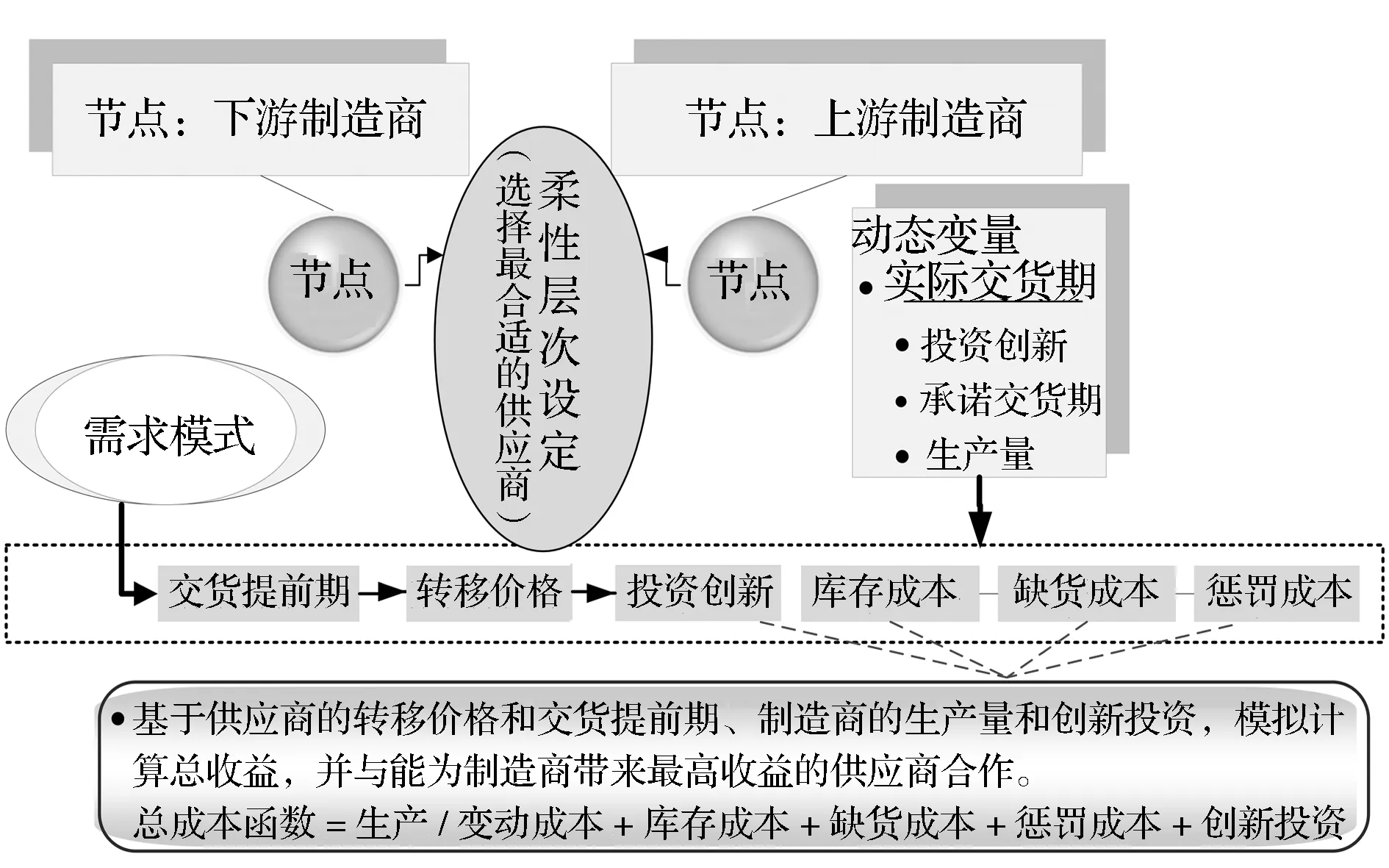
图1 基于供应商选择柔性的动态供应网络架构

然而，当产品/服务的定位(或再定位)和价值结构、资源可得性、运输距离和客户需求发生变化时，动态供应链架构将是非常有利的[4, 13]。假设对于任一给定的订单，总是有几种可行的供应商-制造商供应网络架构来满足需求，不过，对相互信任的担忧而产生的合作意愿强弱仍然是制约柔性化供应网络架构的最大障碍，基于此，笔者进一步假设各个节点都愿意并且能够与供应链中的其他节点进行很好的沟通，信息共享，资源能够在供应网络中平稳流动。

基于供应链路径柔性(即，运用不同的方法或流程计划来生产同一产品或部件的能力)，和示例仿真分析方法[4]，笔者构建了基于供应商选择柔性的动态化供应链框架(如图1)。对于供应商-制造商二

级供应链中的每一个节点，笔者均构建了四阶(i=1，2，3，4)供应链柔性，在柔性理念下，不同示例最终都可以实现完全相同的既定目标。其中，CSi的实际交货期ti是动态变量，对其承诺的交货提前期Tij和AMj的生产量yij、投资创新θij产生动态性影响，而CSi的转移定价策略和AMj的生产量、投资创新决策也在五种战略性转移定价承诺策略(FF、CF、CO、IW和IO)选择中动态变化，并对需求模式、库存持有成本、缺货成本和延期惩罚成本产生直接影响，进而通过对CSi和AMj的利益结构产生影响而推动供应网络的重新架构(如表2所示)。供应网络重构的依据是基于供应链整体利润最大化原则为AMj选择最优的CSi。示例仿真分析利用赋值的方法来描述案例[4]，为了对所提供的网络体系进行对比分析，笔者基于三个不同的柔性层次(NF，PF和MF)而选择了20个示例(如图2～4所示)，除了柔性层次不同，所有这20个示例的其它条件均保持相同。NF是指没有柔性(No Flexibility)，即每个AMj只能与一个供应商合作(如图2示例1-4)；PF是指部分柔性(Partial Flexibility)，即每个AMj可以从指定的几个供应商中选择一个进行合作(如图3示例7-13，图4示例14-20)，这种柔性层次在有效地配置可得资源方面具有较大优势；MF是指完全柔性(Maximal Flexibility)，即每个AMj可以在所有供应商中选择一个进行合作(如图2示例5-6)，这种柔性层次可以实现资源在供应链全局范围的最优化配置。笔者以MF为参照系，据以探讨五种战略性转移定价承诺策略下的供应商选择柔性对交货期、投资创新、生产量和供应商、制造商及供应链整体利润等供应链绩效指标所产生的影响，为柔性环境下的供应链绩效改善提供比较基准与决策依据。

图2 NF与MF下的供应网络架构示例(NF：示例1-4；MF：示例5-6)

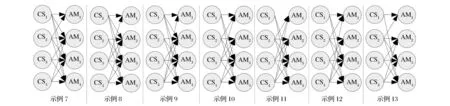
图3 PF下的供应网络架构示例(PF：示例7-13)

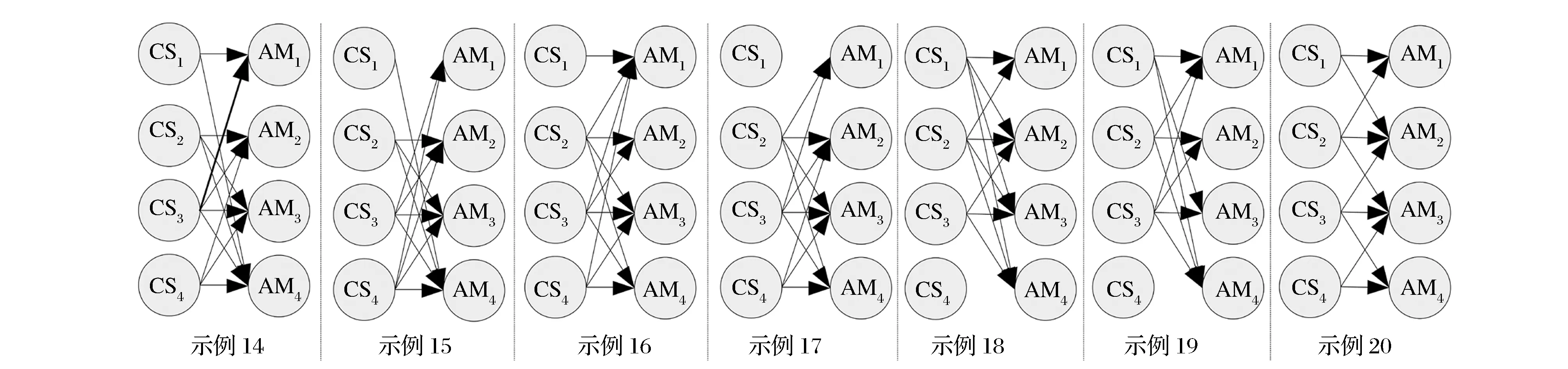
图4 PF下的供应网络架构示例(PF：示例14-20)

表2 变量指标界定

表3 相关变量赋值[4, 10, 11]

为了详细探讨供应链环境下的部分柔性，笔者对不同的路径选择进行了排列组合，在二级-四阶供应网络中，PF前提下共有1194种可能的供应商-制造商组合或者供应网络架构(示例如图3、4所示)。相关变量界定及其赋值分别如表2、3所示。与定性的理论架构相比，定量的数据分析更具有直观性和通俗性[4, 7-8]，因此笔者运用仿真方法对示例进行实证分析(如图5～8)，来探讨供应网络架构中的柔性化特征和动态化控制行为。

3.1 战略性转移定价承诺与供应商的承诺交货提前期决策

在CSi的战略性转移定价承诺与AMj投资决策之间至少表现出如表1第一行所示的五种形态的交互作用，当不存在供应商选择柔性时，FF、CF和IW情形下供应商的承诺交货期Ts均相等，取决于单位产品的库存持有成本α、延期惩罚成本β、缺货成本δ、等待成本ν和实际交货期的平均变动率λ。即，当存在交货期不确定性时，无论CSi保留转移定价弹性，还是实行转移定价承诺策略，其最优的承诺交货提前期保持不变。存在于CSi的战略性转移定价承诺策略与AMj的创新投资之间的交互影响不会影响到CSi的最优承诺交货提前期决策。

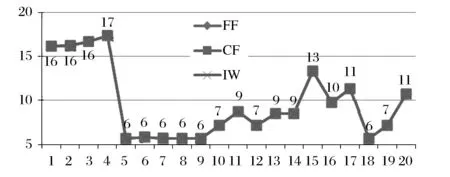
图5 供应商承诺交货期决策Tsij的变化趋势图(NF(1-4)，MF(5-6)，PF(7-20))

而在三种不同层次(NF、PF和MF)的供应商选择柔性情形下，与没有柔性NF(示例1-4)相比，完全柔性MF(示例5-6)与部分柔性PF(示例7-20)下供应商承诺的交货期Tsij具有明显的时间优势。更进一步，通过图5可以看到，虽然MF下的示例5-6具有供应网络全局范围最大的时间优势，但是，PF下的示例7-9、示例18也可通过部分柔性来获得在完全柔性条件下才能实现的最短交货期承诺。

3.2 战略性转移定价承诺与制造商的投资决策

如表1中的第三行所示，在外部环境和合作对象确知的静态环境下，θIW<θCF<θFF，且θIO<θCO<θCF<θFF，由于θ越低，创新投资效率越高，因此可以发现，CSi实行完全转移定价承诺策略可以激励AMj进行更多的投资创新活动；与分散决策系统相比，一体化供应链的创新投资力度将更大一些。

图6a 供应商选择柔性对投资决策θij的影响(NF(1-4)，MF(5-6)，PF(7-20))

图6b 供应商选择柔性对投资决策θij的影响(NF(1-4)，MF(5-6)，PF(7-20))

需要说明的是，受笔者所赋值的影响，FF、CF、IW和IO情形下的投资决策θij之间的区别并不明显，有兴趣的读者可以通过改变赋值来强化这种区别。

3.3 战略性转移定价承诺与制造商的生产量决策

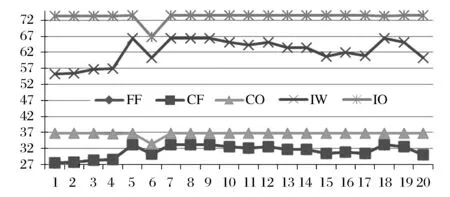
图7 生产量决策yij的变化趋势图(NF(1-4)，MF(5-6)，PF(7-20))

3.4 战略性转移定价承诺与供应链的利润

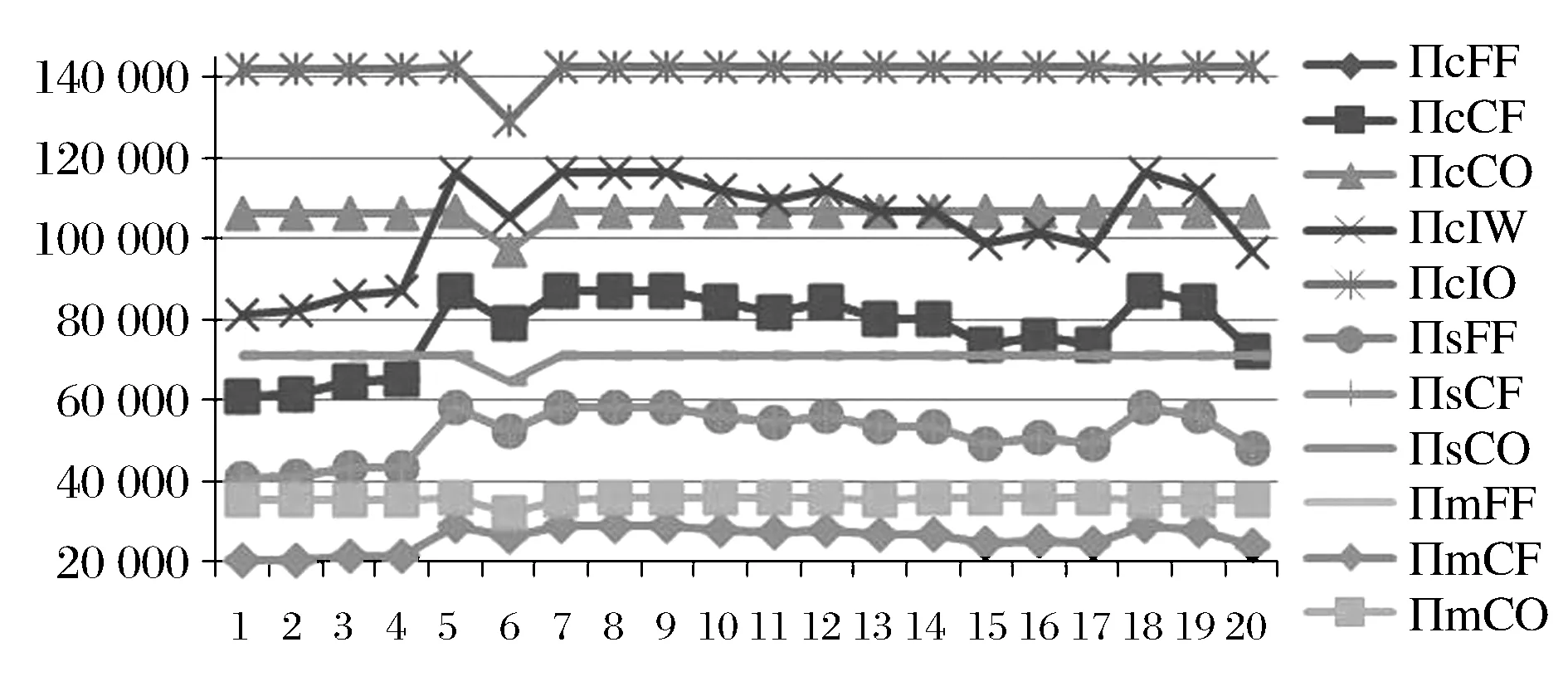
图8 供应商、制造商及其供应链整体利润的变化趋势图(NF(1-4)，MF(5-6)，PF(7-20))

4 结语

在外部环境与合作对象确知的静态环境下，根据合作双方所处的主从地位以及各自对最优决策变量的侧重点不同，上游供应商CSi与下游制造商AMj可以分别通过战略性转移定价承诺、交货提前期决策和生产量、创新投资决策之间的交互作用来为自己争取尽可能最优的合作模式。更深入一步，本文将柔性化思考纳入到这种交互作用之中，探讨存在于这种交互作用之中的供应商选择柔性对交货提前期、投资创新、生产量和供应商、制造商及供应链整体利润所产生的影响，为柔性环境下的供应链绩效改善提供比较基准与决策依据。

在动态变化的环境中，考虑到AMj在不同CSi之间进行选择的柔性化特征，得到如下四个方面的结论：

首先，供应网络架构柔性是供应链整体及其各节点企业获取绩效改善的重要途径，与NF相比，MF和PF情形下的供应链绩效均能得到明显改善，而其中又以MF优势最为突出。当然，PF与MF并不是在任何情形下都能显著改善供应链绩效，如图6b、图7、图8所示，在转移价格和交货期均确知的前提下，三个不同的柔性层次对供应链的创新投资、产量、收益等绩效指标所产生的影响是极其有限的。

其次，虽然PF是供应网络架构中较为可行的柔性层次选择，但是，其与MF一样，容易产生供应网络资源的供给与需求失衡现象，即，出于成本最小或收益最大化考虑，一方面，不同制造商之间可能会竞争同一或少数供应商的资源，而与此同时，部分供应商的资源则会出现闲置。

第三，在静态的供应网络架构中，无论是一体化决策还是分散化决策，承诺的交货期和转移价格均确知的供应网络具有最为明显的利润优势，而在柔性化供应网络架构中，不确定性情境下的一体化决策(上标为IW)与确定性情境下的转移定价承诺决策(上标为CO)对供应链整体利润绩效所产生的影响随着供应网络柔性层次以及供应网络节点企业各自的能力特点(生产成本、延期惩罚等)的不同而呈现不同的特点，进而影响到供应链整体及其各节点的行为取向。

第四，柔性并不是免费的，柔性层次越高，与该柔性层次相适应的柔性投资成本也就越高(这种投资被称之为惩罚成本[4])。由于MF意味着在所有可能的供应网络架构中进行搜寻与取舍，其对时间和资金的要求均很高，可见，MF仅是一种理想的状况。从图5～8可以看到，绝大部分PF情形下的供应链绩效改善与MF情形相同或者接近，所以，现实中更多倾向于采用PF这种柔性层次的供应网络架构思想，这与Wadhwa等[4]的结论是一致的。

本文仅以一个简单的二级-四阶供应链为研究对象，将利润、交货期、产量和投资创新作为供应链绩效研究的关注点，而事实上，供应商选择柔性所涉及的领域很广，在进行供应链决策中需要考虑的因素也很多，如，实际需求的随机变化、库存、订单履行率、配送方式等。在后续研究中，期望将二级供应链向三级、四级进行拓展，并逐步将上述变量纳入考虑范围。

[1] Das K. Integrating effective flexibility measures into a strategic supply chain planning model[J]. European Journal of Operational Research, 211, 201(1): 170-183.

[2] Sánchez A M, Pérez M P. Supply chain flexibility and firm performance: A conceptual model and empirical study in the automotive industry[J]. International Journal of Operations & Production Management, 2005，25(7): 681-700.

[3] Lummus R, Duclos L, Vokurka R. Supply chain flexibility: Building a new model[J]. Global Journal of Flexible Systems Management, 2003，4(4): 1-13.

[4] Wadhwa S, Saxena A, Chan F T S. Framework for flexibility in dynamic supply chain management[J]. International Journal of Production Research, 2008，46(6): 1373-1404.

[5] Gosling J, Purvis L, Naim M M. Supply chain flexibility as a determinant of supplier selection[J]. International Journal of Production Economics,2010，128: 11-21.

[6] Malhotra M K, Mackelprang A W. Are internal manufacturing and external supply chain flexibilities complementary capabilities?[J]. Journal of Operations Management, 2012, 30: 180-200.

[7] Moon K K, Yi C Y, Ngai E W T. An instrument for measuring supply cahin flexibility for the textile and clothing companies. European Journal of Operational Research, 2012, 222(2): 191-203.

[8] Stalk G.Jr. Time-The next source of competitive advantage[J], Harvard Business Review, 1988,66(6):41-51

[9] Lee L, Lee Y S. Pricing and delivery-time performance in a competitive environment[J]. Management Science,1994, 5(40): 633-646.

[10] 杨文胜，李莉. 响应时间不确定下的交货期相关定价研究[J].中国管理科学, 2005,13(2): 56-62.

[11] 冯华，崔元锋，马士华. 战略性转移定价承诺策略与下游创新之间的交互影响研究[J]. 中国管理科学, 2006, 14(1): 61-67.

[12] Karmarkar U. Manufacturing lead times, order release and capacity loading[M]//Graves S, Rinnooy Kan A, Zipkin P. Handbooks in operations research and management science: Logistics of production and inventory. Amsterdam: North-Holland, 1993:287-329.

[13] Porteus E L. Optimal pricing andreturns policies for perishable commodities[J]. Marketing Science,1985, 4(2): 166-176.

[14] Cho K R, Gerchak Y. Supply chain coordination with downstream operating costs: Coordination and investment to improve downstream operating efficiency[J]. European Journal of Operational Research,2005, 162:762-772.

[15] Palaka K, Erlebacher S, Kropp D H. Lead-time setting, capacity utilization, and pricing decisions under lead-time dependent demand[J]. IIE Transactions, 1998, 30 (2): 151-163.

[16] Radjou N.Deconstruction of supply China[J].Supply Chain Management Review,2000,4:30-38.

A Study on the Supplier Selection Flexibility Based on Strategic Transfer Pricing Commitment

FENG Hua1，PANG Mei1,LIU Kai-jun1，WANG Tian-yu2

(1.School of Economics & Management, Wuhan University, Wuhan 430072, China;2.School of Journalism and Communication,Wuhan University,WUhan 430072,China)

There are interactions between upstream strategic transfer pricing commitment and downstream innovation in a supplier-manufacturer channel, which strongly affect supply chain cooperation mode and the partners’ behavior preferences. Based on routing flexibility and supply chain performance dimensions, say, committed delivery lead time, innovation investment, production quantity and profit, in this parer a strategic transfer pricing commitment model is formulated to provide a view of issues concerning supply chain cooperation mode, with combining the above mentioned static interactions and different flexibility levels into dynamic supply network configuration. By so doing, can at least five interactions be identified, say, i) FFFlexibletransfer pricing,Flexibleproduction quantity), ii〗) CF (Committedtransfer pricing,Flexibleproduction quantity), iii) CO (Committedtransfer pricing,Withoutdelivery time uncertainty), iv) IW (Integratedsupply chain,Withdelivery time uncertainty), v) IO (Integratedsupply chain,Withoutdelivery time uncertainty). With considering the supply chain routing flexibility and applying sample simulation analysis method, at least three conclusions can be obtained, I) Flexible supply network configuration is an important method for supply chain partners and supply chain as a whole to obtain performance improvement. Comparing with no flexibility, maximal and partial flexibility can help to improve performance, and maximal flexibility assumes the most priority in this process. II) Although partial flexibility is a feasible flexibility configuration, it arouses disequilibrium of network resources between supply and demand. III) Flexibility level and each partner’s ability are two dominant dimensions to distinguish profit performance between integrated decision with uncertainty and transfer pricing commitment without uncertainty, and further influence the selection of supply chain cooperation mode and behavior preference. Sample simulation analysis in this paper, in which data is partly adopted and modified use for reference of the researches done by Cho and Gerchak[14]and Wadhwa et al.[4]helps to confirm the above deduction and provides a view for further research of the interactions that exist between optimal cooperation modes and behavior preferences.

supply network; transfer pricing commitment; supplier selection; flexibility level

1003-207(2016)02-0038-09

10.16381/j.cnki.issn1003-207x.2016.02.005

2014-03-19；

2014-12-31

国家自然科学基金资助项目(71202119，71001081)；教育部人文社科基金资助项目(09YJC630172)

简介：冯华(1978-)，女(汉族)，湖北人，武汉大学经济与管理学院副教授，博士，研究方向：供应链能力和供应链治理,E-mail:fenghua@whu.edu.cn.

F252.24

A