在中专教材《电工基础》和《电工学》中戴维南定理和诺顿定理特殊情况简述
库万德克,阿依肖力盘
1新疆伊犁职业技术学院;2新疆新源县第一中学
在中专教材《电工基础》和《电工学》中戴维南定理和诺顿定理特殊情况简述
库万德克1,阿依肖力盘2
1新疆伊犁职业技术学院;2新疆新源县第一中学
分析线性有源二端网络中戴维南定理及诺顿定理的特殊情况,并提出自己的意见。
有源二端网络;戴维南定理;诺顿定理
1 问题提出
在中专教材<<电工基础>>和<<电工学>>中戴维南定理及诺顿定理是非常重要的定理,二定理提供了求含源线形单口网络等效电路及VAR的普遍适用形式,是在具体运算中经常用到的重要定理。但是中专教材中并未提到戴维南定理及诺顿定理存在的特殊情况,这里作以说明。
2 问题分析
2.1 戴维南定理
任何线性有源电阻性二端网络NA,可以用电阻RO、端电压为USO的理想电压源串联电路模型来代替,且USO在数值上等于该NA的开路端电压UOC,RO则等于将该NA中所有电源取零(电压源短路,电流源开路)而所有电阻不变的情况下所得无源二端网络NO的等效电阻Rab。如图一:

图一戴维南定理
NA—线性有源二端网络
NP—无源二端网络
NO—NA中所有独立源为零值时所得的网络戴维南定理用具体图示表示如下:
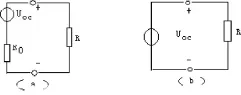
图二
对于戴维南定理,它存在两种特殊情况:
2.1.1 线性有源二端网络的等效电阻RO=∞时
当RO=∞时
I=UOC/(RO+R)=UOC/(∞+R)=0
这时电路等于开路,没有电流流经R,当RO=∞时,这种电路无任何意义,在这种情况下,无戴维南定理等效电路。
2.1.2 线性有源二端网络的等效电阻RO=0时
当RO=0时,证明没有等效电阻存在,可以把RO去掉用导线直接连通,因此,这种线性有源二端网络就可简化成为一条电压源支路。(如图二(b))
2.2 诺顿定理
任何线性有源电阻性二端网络NA,可以用一理想电流源iso与电阻RO并联的电源模型替代,其电流源iso数值上等于该NA输出端ab的短路电流isc,RO则等于NA中所有电源为零时(电压源短路,电流源开路)构成无源二端网络NO的等效电阻Rab,如图三。

图三诺顿定理
NA、、NP、NO、与戴维南定理中的注解相同。
诺顿定理具体图示表示如下:

图四
对于诺顿定理,它也存在两种特殊情况:
2.2.1 当线性有源二端网络的等效电阻RO=0时
当RO=0时(如图四(a))则支路1相当于短路,电流将全部从支路1上经过,而支路2上则完全没有电流,这样的电路无意义,即无诺顿等效电路。
2.2.2 当线性有源二端网络的等效电阻RO=∞时
当RO=∞时,可以认为支路1是断开支路,因此线性有源二端网络就可以简化一条电流源支路,如图四(b)。
3 结束语
以上是戴维南定理及诺顿定理中存在的四种特殊情况,中专教材中并未提到,虽然对中专学生不要求计算与解释特殊情况下的戴维南定理与诺顿定理,但是二定理中均使用了“任何线性有源二端网络……”,学生在学习时,这往往会给学生造成一种假象,使之误解,为只要是线性有源二端网络都存在戴维南定理与诺顿定理的等效电路。但是通过上述四种论述,我可以看出,当条件特殊时戴维南定理(当R0=∞时)的诺顿定理(当R0=∞时)都存在着无等效电路的情况。
因此,虽然中专教材中没有提到这四种特殊情况也不要要求学生掌握,但是作为任课教师我们在教学过程中要给学生提到、讲到,以避免学生在进行深一步的学习时出现不应有的麻烦。

