最隐蔽路径和最聚人气路径模型的求解研究

杨 琴，刘鹏程，罗 静

（1.地理过程分析与模拟湖北省重点实验室, 湖北 武汉 430079；2.华中师范大学 城市与环境科学学院,湖北 武汉 430079）

最隐蔽路径和最聚人气路径模型的求解研究

杨 琴1,2，刘鹏程1,2，罗 静1,2

（1.地理过程分析与模拟湖北省重点实验室, 湖北 武汉 430079；2.华中师范大学 城市与环境科学学院,湖北 武汉 430079）

基于道路通行车辆对其周边人口及环境的影响，提出最隐蔽路径模型和最聚人气路径模型，详细给出了两种路径成本属性的计算方法和各种路径具体求解过程。结合武汉市道路网进行实验分析，比较了不同路径下的距离、人口差异及其原因。结果表明，模型具有合理性和可操作性，可为军事、金融、媒体、公交等路径选择提供理论参考和具体计算方法。

最低成本路径；最隐蔽路径；最聚人气路径

最低成本路径是指在道路网络中从起点到终点所耗费某类资源最少的弧段串，由于所考虑的资源类型不同，最低成本路径可以是时间最短、距离最短、费用最低等路径[1]。最低成本路径在公众出行、城市规划、电力传输、交通管理、军事调度等领域都有重要应用[2-5]。对于最低成本路径的计算和选择，国外研究较早，Stefanakis和Kavouras[6]早在1995年就基于DEM数据，以坡度为行进的阻抗，获取了最快路径。同样基于栅格DEM数据，Lee和 Stucky[7]将通视域和最低成本路径相结合，提出了最大可视域路径的计算方法，保证选择的路径能目睹最大面积的区域。Chandio[8]等从经济学的视角采用多成本决策标准，给出了山坡上最适宜发展路径的计算方法。国内也有相关研究，如王卉[9]等针对雨雾天气下的动态交通路径问题，以能见度为考虑因素，构建了从起点到终点的最佳路径，为人们在恶劣天气下选择道路提供了依据。王云鹏[10]等针对危险品运输中的安全问题，提出了危险化学品运输风险最小路径模型。翁敏[11]等和廖楚江[12]等在考虑公交线路最少换乘和距离最短的基础上，提出了最优出行路径和算法，为居民日常出行提供了方便。

如今，物流业、公共交通以及公众出行对路径的选择，除了考虑主体的需求和感受外，有时候也需要考虑所选择的路线对周围环境和居民的影响。例如，已确定起点和终点的公交运行线路的选择，考虑更多的是居民乘车的方便；晚间超大货运卡车路线的选择，考虑更多的是最大限度减少受噪声影响的人数。基于此，本文提出了最隐蔽路径和最聚人气路径的概念，并给出了求解方法。一般而言，商业宣传、物流、公交线路等会选择最聚人气路径，来达到宣传效果的最大化、物流运输效率的最高化以及为更多人提供公共交通服务，而军事调度、金融、危险品的运输等则会选择最隐蔽的路径，以便运输的隐蔽、安全以及尽量减少受影响居民的数量。

1 模型建立

1.1 最短路径模型

对于用三元组G=＜V，E，W＞表示的路网，其中V是节点集合，E是弧段的集合，W为成本的集合。对于任何弧段ek=（vi，vj）∈E（k为弧段的标号）, W（ek）表示弧段ek的成本。最短路径模型为[11]：

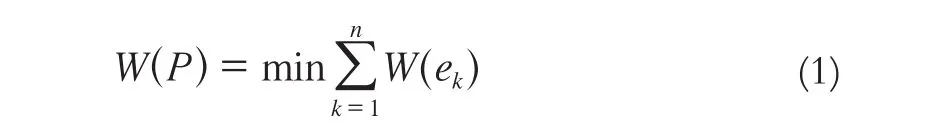
式中，W（P）为最小成本，P为对应的最小成本路径。给定实际的距离值、影响人数及不同属性作为弧段的成本，便可求出最短路径、最隐蔽路径以及其他路径。式（1）常采用Dijkstra模型求解,其基本思路是由近及远寻找起点到其他所有节点的最佳路径，直至达到目标终点[12]。

1.2 成本计算

本模型网络拓扑数据结构中各弧段的成本属性为通行在该路段所影响的人数，该属性的计算是本文两类路径求解的关键。

1.2.1 最隐蔽路径成本计算

最隐蔽路径是指从所选起点到终点影响人数最少的路径。在最隐蔽路径的求解中，必须根据城市一定行政区划（如街道）的人口数量及分布计算路网中每个弧段的影响人数（W（ek））。

对道路网中的所有弧段作缓冲区分析，由于各等级道路的通行能力、影响范围存在差别，因此缓冲区的宽度也不相同。表1第5列是本文拟定的各类道路缓冲区的宽度：国道等级最高，宽度为500 m；乡道等级最低，宽度为150 m，道路等级越高，道路影响范围越大。对于道路网中的弧段k，其缓冲区人口密度按其所在行政单元的人口密度计算，求得缓冲区人口数作为弧段k的W（ek）值。弧段属性的具体计算过程如下：

1）计算各行政单元的人口密度：

式中， si表示某行政单元的面积；mi为某行政单元的人数；pi为人口密度。

2）计算缓冲区在某行政单元内的人数：

式中，xij表示缓冲区与某行政单元相交的面积；mij是缓冲区在该行政单元内的人数。

3）计算弧段k的缓冲区总人数：

将缓冲区在各行政单元的影响人数累加，求得该条道路k的影响人数，即道路k成本W（ek）。

1.2.2 最聚人气路径成本计算

最聚人气路径指从所选起点到终点，距离相对较短影响人数最多的路径。最低成本路径是求取成本累计和的最小值，因此无法直接求解，需要构造特定属性值，本文以单位影响人数对应的长度作为属性（如式（5））。该属性值和影响人数属性呈反向变化，即该属性值越小，影响人数最多，以保证Dijkstra模型求解最短路径的顺利实施。

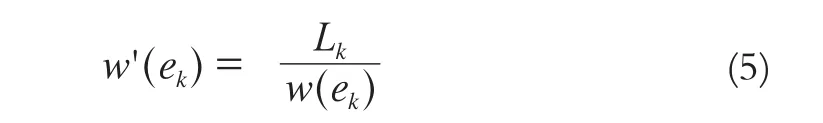
式中， w'（ek）表示新属性；w（ek）表示弧段k的影响人数；Lk是道路k的长度。将道路长度与道路影响人数的比值作为成本，计算能使累计和达到最小的路径即为最聚人气路径。要使累积和最小，即Lk数值相对小，而w'（ek）相对大。

2 案例介绍与分析

2.1 数据处理

选取武汉市道路网进行分析，包括国道、省道、县道、乡道、城区主干道及次干道。由于高速公路的封闭性，构建道路网络时与其他道路不具备连通性，将其排除在外。武汉市面积8 494 km2，常住人口1 073 万人（2010年）。道路总长约为6 000 km，人均道路长度约为0.72 m。在各等级道路中乡道最长，城区主干道最短。因城区人口集聚，城区主次干道影响的总人数和单位长度影响人数最多。各等级道路长度、单位长度影响人数、缓冲宽度等属性见表1。

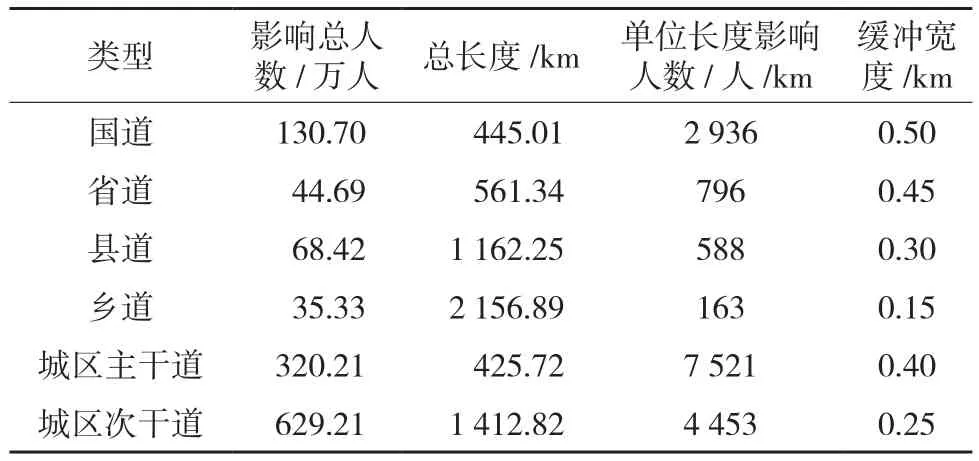
表1 武汉市道路类型属性表

本实验在1∶40 000的比例尺下采用墨卡托投影建立数据库，数据处理的具体步骤如下：

1）数据预处理。对武汉市行政区矢量化，道路数据在2009年武汉市公路地图的基础上参考Google地图予以修正，利用ArcGIS 10.1对武汉市道路网配准、矢量化并进行拓扑检查，正确构建拓扑关系，保证网络的连通性。图1为武汉中心地区不同等级道路图。为进行网络分析，预先进行了数据整理。

2）成本计算。将武汉市道路网按道路等级作缓冲分析，不同等级道路缓冲宽度参照表1。图2为不同道路按等级建立的缓冲区。根据武汉市各乡镇街道人数（2010年），按式（2）计算出武汉市各乡镇街道的人口密度。

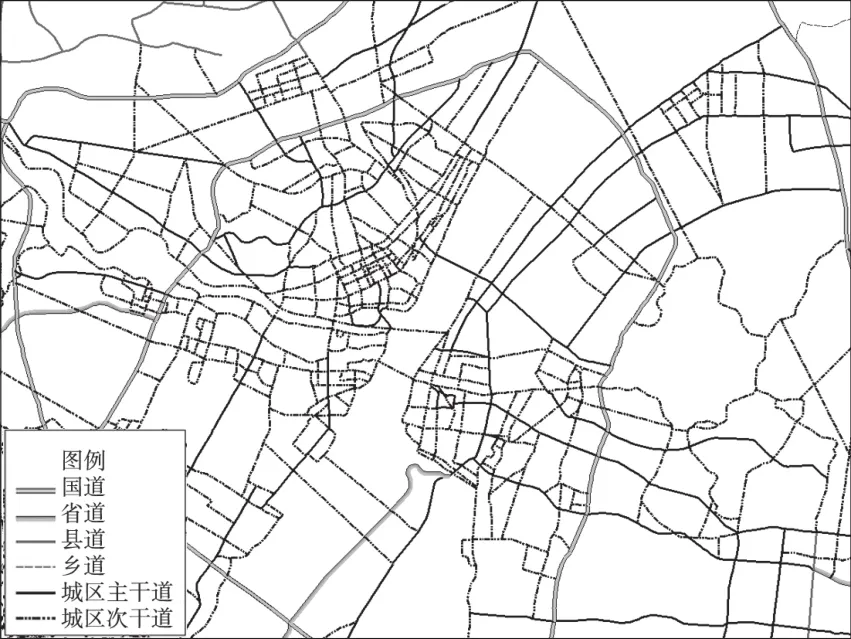
图1 武汉市中心局部道路等级图

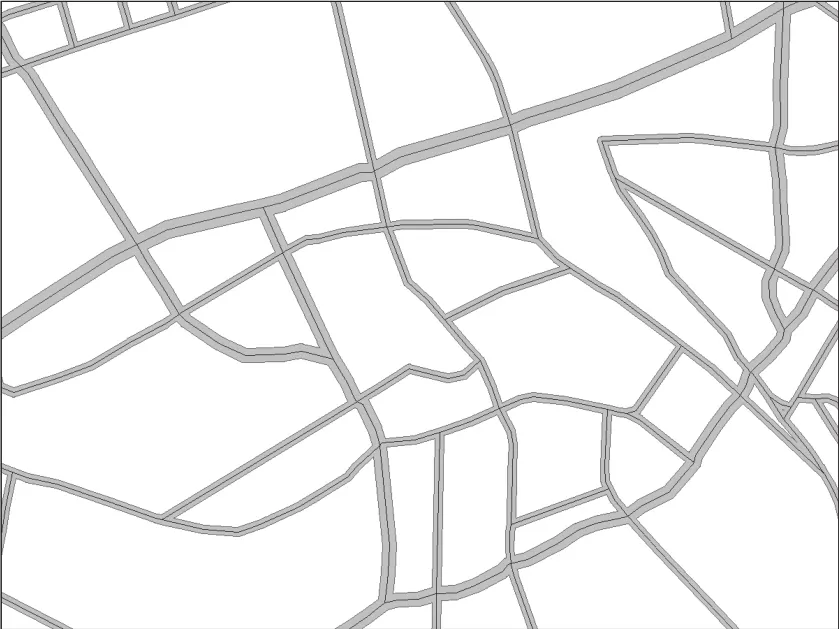
图2 道路分等级建立缓冲区

将缓冲区域作为各等级道路影响范围，结合武汉市乡镇街道的人口密度数据进行叠加分析，求取各等级道路缓冲区域与乡镇街道相交的区域xij，根据式（3）计算各乡镇街道内道路缓冲区域人口数量mij。图3是叠加分析后的效果图，颜色越深，表示人口密度越高，显然，武汉市中心城区道路人口密度最高。对mij累加求和得到道路弧段k的影响人数，作为最隐蔽路径的成本。图4给出了通过三维立体图展示的路径的成本（影响人数），图中道路影响人数密度越大，高度越高。武汉市中心城区人口密度高，道路网密集，道路影响人口密度大。最聚人气路径的成本可在道路影响人数的基础上计算得出，根据式（5）计算得出各道路长度与其影响人数的比值，作为最聚人气路径的成本。

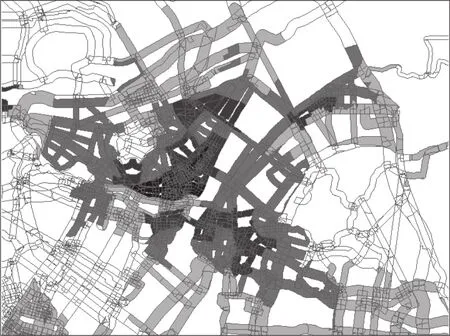
图3 道路缓冲区域人口密度

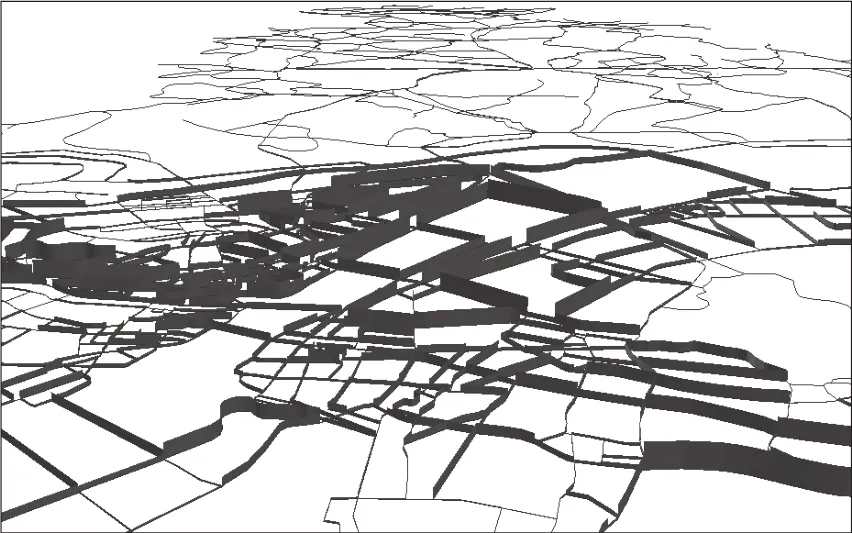
图4 武汉局部道路单位长度人数三维显示

2.2 实验结果与分析

2.2.1 实验结果

根据武汉市道路要素创建网络数据集，分别以道路长度、道路影响人数以及距离与影响人数的比值（单位影响人数对应的路网长度）为成本计算起点与终点间的最短路径、最隐蔽路径和最聚人气路径，选择了3个案例进行了实验。案例1是夜间超大货运卡车运输路线问题，为减少卡车噪声对周围居民的影响，选择走最隐蔽路径。以武汉市体育中心为起点，武汉天河机场为终点进行计算。案例2是光谷广场的某超市为确定超市接送车线路，需要选择从光谷广场到汉口火车站的路线，为最大限度地方便沿途顾客，需选择一条影响人数最多的路径即最聚人气路径。实验中计算了光谷广场到汉口火车站的最聚人气路径，同时计算出最短路径、最隐蔽路径作比较。案例3是政府为宣传的需要，以汤逊湖生态旅游区与四美塘公园为起点和终点，为达到宣传效果的最大化，宣传车必须选取一条影响人数最多的路径。实验中对3条路线分别计算了最短路径、最隐蔽路径以及最聚人气路径，计算结果数据如表2所示。图5中①表示最短路径，②表示最隐蔽路径，③表示最聚人气路径。

表2 实验结果比较

从表2可知，案例1中最隐蔽路径比最短路径长11.52 km，但在影响人数上，只有最短路径影响人数的40%；最隐蔽路径比最聚人气路径长约6 km，但影响人数只是后者的1/3。由此可知，虽然最隐蔽路径需要更长的距离到达目的地，但是影响人数却大大减少，在实例1中为可行路线。案例2中最聚人气路径距离介于最短路径和最隐蔽路径之间，虽然比最短路径长约50%，但是道路的影响人数达到62万多，是最短路径影响人数的2倍，最隐蔽路径的5倍多。可见，选择这条最聚人气路径才能为更多的顾客提供方便。对于人口密度高且相近的城区，如何选择一条人口影响数量多的道路，有效性更为显著。案例3中最聚人气路径影响人数最多，但距离只比最短路径多5 km；最隐蔽路径最长，但是影响人数远低于最短路径，占最短路径影响人数的19%；最聚人气路径与最隐蔽路径影响人数相差5倍多。宣传车在循环行驶中可根据实际情况选择合适的路线。

2.2.2 实验分析

为验证图5路径计算结果，通过图6并结合表2中路径所经区域平均人口密度对3个案例的路径进行分析。图6表示3个案例中各路径从起点到终点依次经过的节点间道路单位长度影响的人数，其中横坐标表示依次经过的道路的序号，即式（1）中的弧段标号 k。图6a中3条路径单位长度影响人数先增后减，符合案例1从武汉市体育馆出发，经过中心城区到达郊区的天河机场，人口密度先高后低的实际情况；最短路径与最聚人气路径单位长度影响人数的变化基本一致，因而在计算结果中2条路径比较接近；最隐蔽路径与其他2条路径单位长度影响人数的差异先大后小，因而计算结果中前半段3条路径各异，到后半段路径出现重合部分。图6b中3条路径单位长度影响人数变化曲线无重合，因而路径各异；3条路径影响人数的趋势都是先增后减再增，符合图5计算结果从武昌到汉口，经过长江，人口密度变化为高低高的实际情况。图6c中最隐蔽路径与其他2条路径所经区域人口密度的均值远低于其他2条路径，道路单位长度影响人数也最低，因而计算结果中与其他2条路径的差异明显；最短路径与最聚人气路径道路单位长度影响人数的变化基本一致，故计算结果差异也较小。

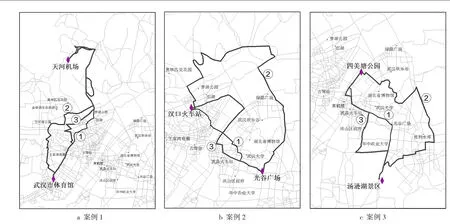
图5 路径计算结果

综合3个案例，虽然路径所经道路单位长度影响人数是波动的，但总的来说，最隐蔽路径所经区域人口密度值最低，单位长度影响人数也最低；最聚人气路径所经区域人口密度最高，影响人数也最多。由此可知，道路所经区域的人口密度与道路影响人数呈正相关。

通过模型的计算产生的最隐蔽路径会选择人口密度低的区域，经过的道路单位长度的影响人数都较低，因而影响的总人数也最低；最聚人气路径反之，且在3 个案例中路径单位长度影响人数曲线都与最短路径相近，保证了影响人数最多距离相对较短，表明模型建立的可行性。

图6 路径所经道路单位长度影响人数变化图

3 结 语

为解决车辆多种路径选择需求的问题，本文提出了最隐蔽路径和最聚人气路径模型，结合实例进行分析比较，验证了模型的合理性和可操作性，在军事、金融、物流、媒体、公交等路径选择决策时，具有一定的参考价值。

由于数据等方面的限制，模型尚有不完善之处：首先因高速道路的封闭性及处理中的复杂性，模型构建没有将其包括在内。其次，缺乏详细的道路行驶方向、单双行道数据，模型没有对此设限制。最后，未考虑人口的流动性，道路是否施工，能否通行等实际情况，模型的适用性还有局限。技术的发展与完善将进一步完善本文提出的道路影响人数的获取方式。在大数据热潮下，将可通过通信位置等方式，获取道路影响人口的实时分布状况，这也是下一步研究的重点。

[1] Effat H A, Hassan O A. Designing and Evaluation of Three Alternatives High Way Routes Using the Analytical Hierarchy Process and the Least-cost Path Analysis, Application in Sinai Peninsula, Egypt[J]. The Egyptian Journal of Remote Sensing and Space Sciences, 2013(16):141-151

[2] Adriaensen F. The Application of ‘Least-cost’ Modeling as a Functional Landscape Model[J]. Landscape and Urban Planning, 2003, 64(4):233-247

[3] Douglas D H. Least-cost Path in GIS Using an Accumulated Cost Surface and Slope Lines[J]. Cartographic: the International Journal for Geographic Information and Geovisualization, 1994, 31(3): 37-51

[4] Motemurro D, Barnett S, Gale T.GIS Based Process Helps TransCanada Select Best Route for Expansion Line[J]. Oil Gas,1998,96(25): 63-71

[5] Bagli S, Geneletti D, Orsi F. Routing of Power Lines through Least-cost Path Analysis and Multicriteria Evaluation to Minimize Environmental Impacts[J].Environ Impact Assessment Review, 2011(31):234-239

[6] Stefanakis E, Kavouras M. On the Determination of the Optimum Path in Space[J]. Spatial Information Theory a Theoretical Basis for GIS,1995,988:241-257

[7] Lee J, Stucky D.On Applying Viewshed Analysis for Determining Least-cost Paths on Digital Elevation Models[J].International Journal of Geographical Information Science, 1998,12(8):891-905

[8] Chandio,I A. Computer Application in Routing of Road Using Least-cost Path Analysis in Hillside Development[J]. Research Journal of Environmental and Earth Sciences,2012,4(10):907-911

[9] 王卉,郭健,阚映红.GIS 中顾及能见度影响的最优路径研究[J].测绘科学技术学报,2014, 31(2):185-189

[10] 王云鹏,孙文财.基于ArcGIS的危险品城市运输路径优化模型[J].吉林大学学报:工学版,2009,39(1):45-49

[11] 翁敏,毋河海,杜清运,等.基于公交网络模型的最优出行路径选择的研究[J].武汉大学学报：信息科学版,2004,29(6):500-503

[12] 廖楚江,蔡忠亮,杜清运,等.基于最少换乘的公交最优路径算法的设计与实现[J].武汉大学学报:信息科学版,2006,31(10):904-907

[13] 朱长青,史文中.空间分析建模与原理[M].北京:科学出版社,2006

[14] 刘湘南.GIS空间分析原理与方法[M].北京:科学出版社,2005

P208

B

1672-4623（2016）03-0056-04

10.3969/j.issn.1672-4623.2016.03.018

杨琴 ，硕士，研究方向为地理制图与时空数据挖掘。

2015-04-21。

项目来源：国家自然科学基金资助项目（41371183）；教育部人文社科规划资助项目（12YJAZH222）。