电梯对重—导轨系统的抗震措施试验研究及分析

吕风英朱 彤万 会

(1.河北丰宁抽水蓄能有限公司 承德 068350)

（2. 大连理工大学 建设工程学部 大连 116024）

电梯对重—导轨系统的抗震措施试验研究及分析

吕风英1朱 彤2万 会2

(1.河北丰宁抽水蓄能有限公司 承德 068350)

（2. 大连理工大学 建设工程学部 大连 116024）

地震时，电梯对重脱轨主要由于导轨动力响应过大造成。为了解地震时电梯导轨在有无保持装置时的动力响应差异，对一段带有对重和导轨的局部足尺模型进行了振动试验，并利用有限元软件ANSYS对试验进行数值模拟。结果表明，有限元结果和试验结果吻合较好,证明了所建有限元模型的正确性；同方向同幅值地震激励时，安装保持装置的导轨动力响应比无保持装置的小，且保持装置使导轨动力响应有均化趋势，这些都会有效地防止实际地震时电梯对重脱轨。

对重脱轨 保持装置 足尺模型 振动试验 数值模拟

电梯在地震中的安全性能对建筑物中的人员以及财产的安全都非常重要，开展电梯结构的抗震性能试验研究对于保障国家生产的正常发展和人民的生命财产安全有着重要的意义。地震时，高层建筑的电梯会受到不同程度和不同形式的损害，多次震后数据[1-2]统计表明，电梯对重脱轨是比例最高的破坏形式，脱轨的对重和轿厢往复碰撞，会带来二次伤害，造成更大的人员伤亡和财物损失。

国外由于高层建筑发展较早，对电梯的抗震研究较早且较多[3-5]。Mahendra P. Singh[5]采用Lagrange方程建立了对重—导轨体系的耦合振动方程，将地震激励以楼层惯性力施加在对重系统上；Yang T.Y，Kullegowda H等[3]同时做了对重—导轨体系的模型试验和数值模拟，并对两者结果进行对比，但其模型是缩尺模型。国内也有人做了相关的研究[6-8]，但与国外研究方法一样，偏于现象总结和理论解析推导。他们通过理论解析推导出电梯在地震波激励下的动态响应规律并提出一些抗震和防脱轨的措施，在一些措施中，提高构件强度和接触部位的柔性对抗震效果是显然的；多数文献提到防对重脱轨装置，但未对其进行试验或是数值验证。国内在2015年编写的《地震情况下的电梯要求》[9]提到了保持装置(一种防脱轨装置)。本文基于此，用试验和数值模拟去探究保持装置的作用。

试验可以得到模型在地震激励下有无保持装置的定量结果，数据对比具有一定的说服力。此次试验为增加结果的可靠性，采用足尺模型，分有无保持装置的试验模型在不同方向、不同级别的实测地震波下进行地震激励试验。最后用有限元软件ANSYS进行数值模拟，以达到数值和试验相互验证的目的。

1 试验概况

1.1 试验模型的确定

电梯的导轨—支架可看作带有弹性支撑的连续梁，连续梁上的碰撞力或是位移激励有一定的影响范围。计算表明，当连续梁超过三跨后，荷载对连续梁产生的作用效果基本一致，所以在试验模型中选择三跨导轨会产生最好的结果，局限于试验环境和条件，并且两跨和三跨连续梁在动荷载下的响应效果差别也不是太大，所以选择两跨导轨。

把导轨—支架体系焊接于一钢性框架上，并将对重通过钢索悬挂于外框架的顶梁上，那么试验外框架相当于建筑物，地震作用通过振动台面传给外框架后，外框架通过支架将振动传递到导轨上，从而使导轨和对重相互撞击，这样的地震响应试验与实际有一定差异，但振动传递规律和实际一致，所以得到的导轨反应规律也将相似于实际地震时对重—导轨耦合振动效果。

多数电梯厂家在对重侧使用固定滑动导靴和空心导轨以达到节省成本的目的，这也是对重在地震中容易脱轨的主要原因。所以本次试验中采用TK5A型空心导轨和固定滑动导靴。

图1为本试验的重要构件—保持装置，保持装置类似于导靴上的挡板，位置处于对重块中部。电梯正常运行时，保持装置与导轨没有接触，地震激励时，对重和导轨相互撞击，保持装置发挥作用。

图1 保持装置

试验外框架(2.5×2.5×6m)采用Q235钢；对重所用材料为53个铸铁块，总重2014kg；钢丝绳、绳头组合以及导轨等均采用原结构材料。模型外框架底部焊接在20mm厚钢板制成的底座上，再通过高强螺栓与振动台相连接。图2为试验模型的整体照片。

图2 振动试验模型

1.2 试验设计

试验在大连理工大学水利工程学院抗震实验室的振动台上进行。图3为试验测试系统组成的示意图，试验中采用MTS振动控制系统输入地震动激励；采用MDR加速度测量分析系统采集加速度信号；NI-PXI应变测试仪采集应变；非接触视频测量系统采集位移。

试验包括白噪声扫频和地震波激励试验，扫频研究模型在有无保持装置下的基频变化；地震波激励试验研究模型在有无保持装置下的加速度响应、应变响应以及导轨变形响应的变化。扫频用小振幅白噪声信号驱动振动台，进行频率扫描；汶川地震中电梯大量受损，所以地震激励试验采用2008年汶川地震于茂县实测的地震波，图4为此地震波的加速度时程曲线，由于试验采用足尺模型，所以地震波不用相似转换。

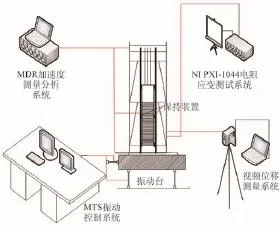
图3 试验示意图

图4 输入的茂县波时程曲线

试验中将地震波加速度峰值调整为0.3g、0.4g、0.5g；定义垂直于对重面方向为X，平行于对重面方向为Y(见图2)，分别沿X、Y两个方向输入地震波。表1为试验工况。

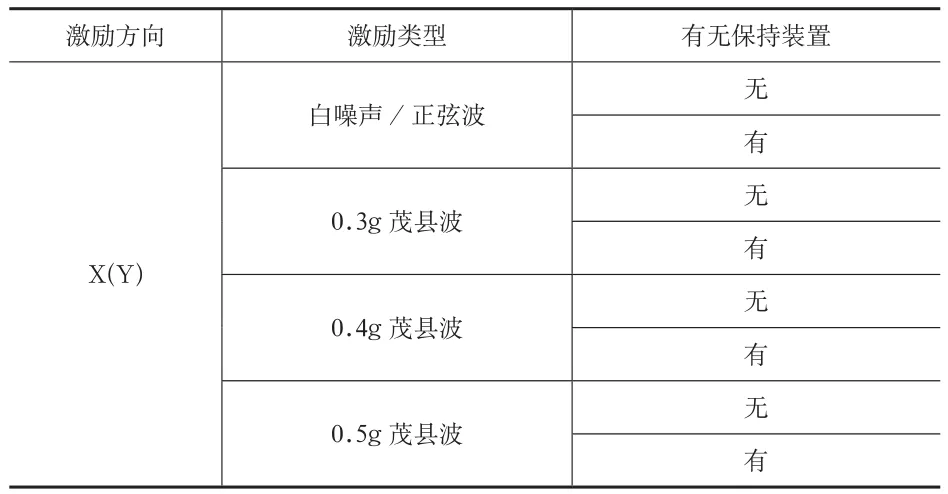
表1 试验工况

1.3 测点布置

●1.3.1 加速度测点布置

为方便对不同工况下的加速度响应进行对比，所有工况加速度传感器布置方案一样，图5给出加速度传感器布置示意图。1~7号传感器均匀布于整个导轨，由于结构和激励输入方向的对称性，只布置其中一个导轨；8号传感器位于外框架顶梁，以测定外框架的动力响应；9号传感器位于对重重心位置，测定对重的动力特性；10号传感器布置在振动台面上以检测地震激励输入的正确性。

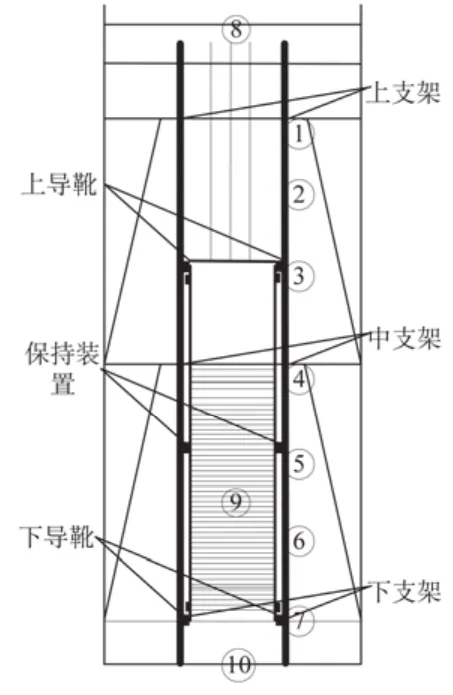
图5 加速度传感器布置图

●1.3.2 应变测点布置

应变测点主要布置在左、右导轨的上、中、下支架以及保持装置附近，考虑到地震输入时导轨结构的响应以受弯变形为主，因此，各应变测点主要布置在导轨的两翼以及腹面上，以尽量保证可以测试到结构振动产生的最大应变。结构模型应变测点布置图以及局部详图见图6。

●1.3.3 位移测点布置

采用英国Imetrum有限公司生产的GigE.117fp非接触式视频位移测量分析系统对处于下跨导轨上的编号为4~7的四个加速度传感器位置及下跨导轨的中部位置共5个点(见图5)进行位移实时测量。

2 试验结果分析

2.1 模型卓越频率分析

向振动台输入白噪声波，并对结构上某点加速度时程做傅里叶变换可以得到该点所属结构的卓越频率，由于本试验模型为多个构件的组合结构，所以不同构件上的加速度测点将得到不同的频率信息。

所有加速度测点做傅里叶变换得到三个主要的结构卓越频率，通过输入这三个频率的小幅度正弦波，确定三个频率分别属于对重、外框架和导轨，并且有无保持装置下，试验模型的X向和Y向扫频结果基本一样，说明保持装置对模型结构影响很小且结构对称性较好，结果见表2。

表2 试验模型的卓越频率

2.2 导轨加速度响应

定义加速度放大系数为某测点加速度时程曲线峰值与台面加速度峰值的比值。图7为两个方向上，导轨上加速度测点放大系数沿高度的分布。

由图7可以得到如下结论：

1）导轨与支架(测点高度0.5m，3m，5.5m)结合部位测点加速度响应较小，每跨导轨中部位反应较大；同样峰值的激励，同位置测点反应Y向大于X向。

2）同样幅值地震波激励下，不管是X向还是Y向，有保持装置测点反应均小于无保持测点反应，所以，加装保持装置对抑制导轨振动有一定的作用。

表3列出两个方向各级别地震激励下最大的加速度放大系数减小百分比。

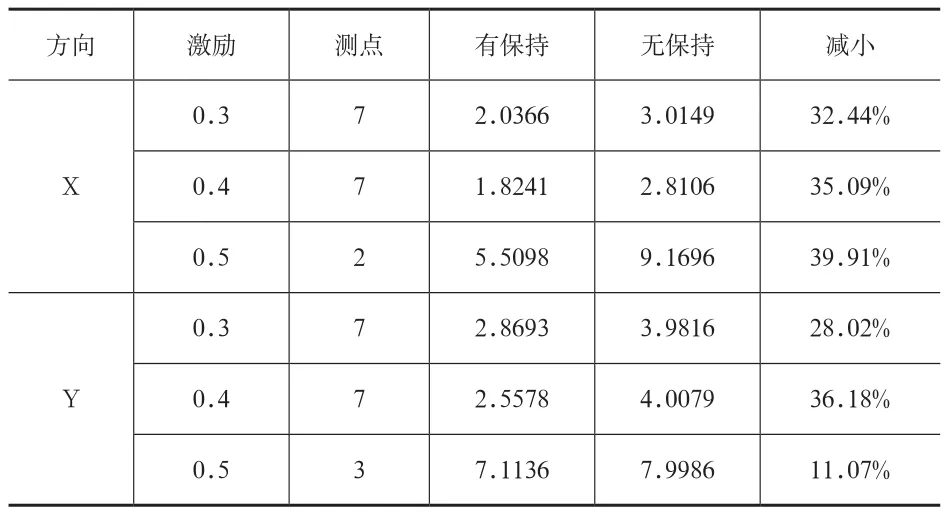
表3 加速度放大系数对比

由表3可以看出，加速度放大系数减小百分比最多的测点大部分为7号测点，7号测点为下支架位置，说明保持装置对抑制导轨下部振动的作用更为明显；每个方向下，加速度放大系数减小百分比有增大趋势，说明强震时，保持装置的抑制作用可能更为明显。

2.3 导轨应变响应

试验结果表明，X向输入激励时，导轨翼缘应变大于腹面应变；Y向激励时，腹面应变略大于翼缘应变；导轨支架上应变很小。图8给出导轨上测点应变响应峰值沿高度变化，其中X向由导轨上奇数号测点结果组成，Y向由导轨上偶数号测点结果组成。

图8 应变峰值沿导轨分布

由图8可以看出：

1）两个方向上导轨动应变响应分布规律不同，X向时下支架部位反应较大，Y向时上导靴位置较大；当基础输入同等幅度的地震波时，沿X向激励产生的动应变幅值大于沿Y向激励产生的动应变幅值。

2）保持装置对动应变响应有影响，同方向同幅值激励时，最大应变测点幅值降低明显，虽然保持装置附近点应变由于保持装置的撞击而增大，但它却使整体导轨动应变响应有均化的趋势。

表4列出激励幅值为0.5g时，两个方向各测点应变峰值增大或者减小百分比。

由表4可以看出，有保持装置相对于无保持装置的动应变峰值有增大也有减小，但是减小幅度小于增大幅度，且保持装置位置的测点由于保持装置的撞击而增大，但整体上导轨应变有减小趋势。

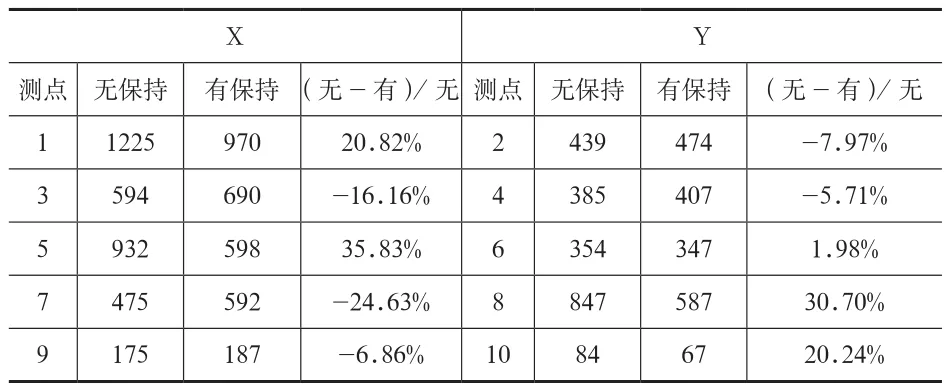
表4 应变响应对比

2.4 导轨变形响应

非接触视频测量仪器测得的位移为空间绝对位移，以7号加速度测点(下支架)为基点求其他位移测点的相对位移，即导轨变形。图9为有无保持装置下导轨变形。

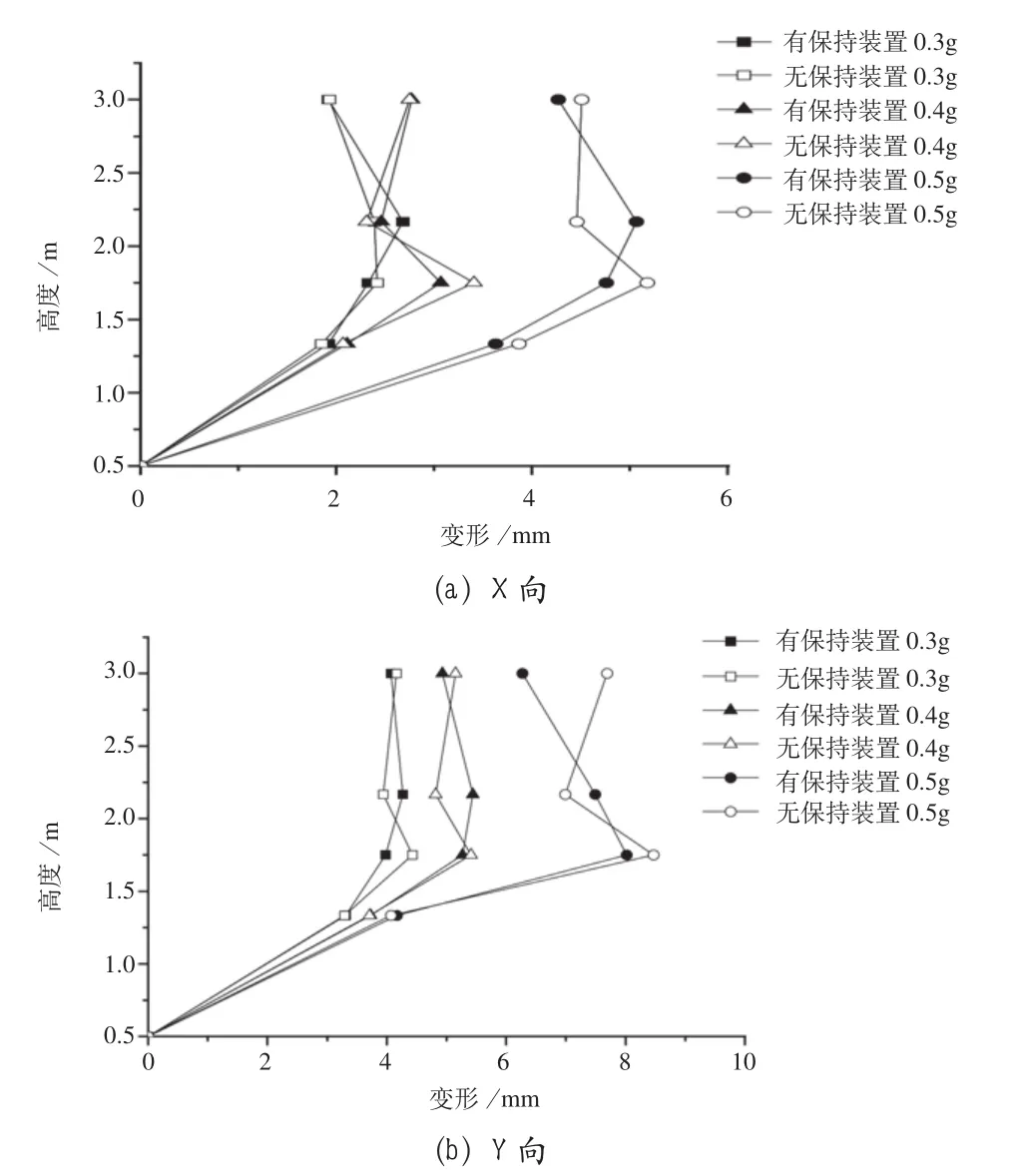
图9 导轨变形

由图9可以得到：

X向激励时，导轨变形在1.75m处较大；而Y向激励时变形分布比较均化。

加装保持后，台面输入幅值相同激励时，保持装置测点(距离台面2.167m)变形相对无保持状况略有升高，但其他测点变形普高减小，此现象在X向振动时更为显著，最大减小11.7%，说明保持装置可以降低导轨的动力变形。

3 有限元模拟分析

ANSYS是一套基于有限元方法的数值模拟软件。数值模拟中涉及到导轨和对重导靴、保持装置的接触碰撞非线性，针对非线性分析，ANSYS能选择合适荷载增量和收敛准则。

3.1 有限元模型的建立

外框架上构件的连接采用刚结，导轨和支架的连接通过节点耦合自由度达到铰结，外框架和导轨均采用BEAM44单元；悬挂对重的绳索采用LINK10单元，开启受拉模式，并带有预应力；将对重和对重架简化为一均质连续体，采用SOLID45单元，弹性模量适当扩大以使对重近似刚体运动。

合理碰撞模型的建立是分析碰撞动力响应的的前提，Jankowski[10,11]在一系列碰撞研究中指出碰撞模型刚度和阻尼取值合理的情况下，Kelvin模型得出的数值结果和试验结果有较好的吻合，所以采用接触单元法中的Kelvin模型模拟对重导靴、保持装置和对重的碰撞。ANSYS中可以采用COMBIN40单元来代表Kelvin模型。

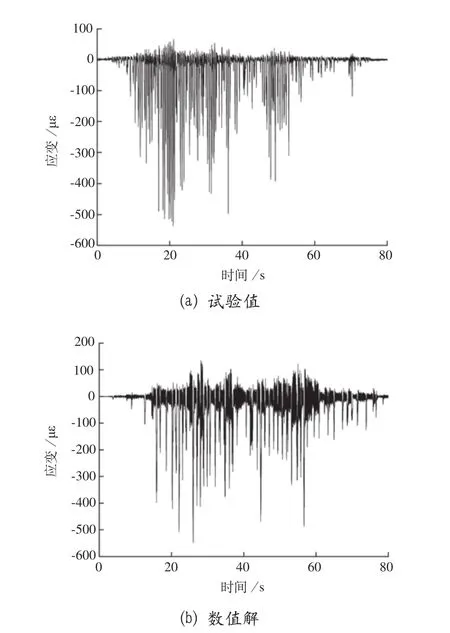
图10 应变时程对比

COMBIN40单元的弹簧刚度和阻尼采用相关经验[12]得到估计值，通过刚度和阻尼参数的调整，当弹簧刚度取值1×105N/m，阻尼取1446 N·s/m时，数值结果和试验结果比较吻合。见图10，图10为0.3gY向茂县地震波激励下，导轨4号测点应变时程曲线的数值解和试验值的对比，曲线下凸是由于Y向地震响应时，对重对导轨的撞击为单向。

3.2 卓越频率的对比

有限元中，用弹簧单元代替碰撞接触点，非线性模态可以求解，试验值和数值解对比见表5。

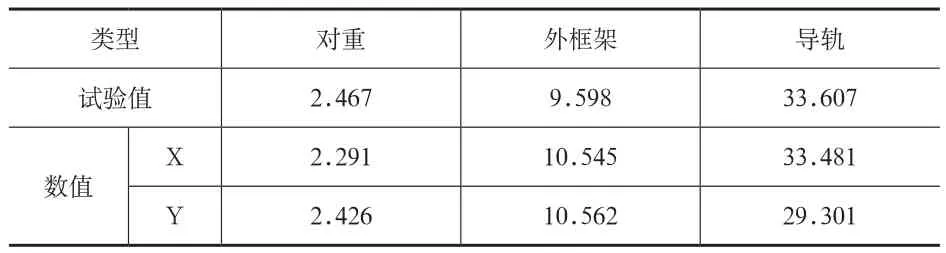
表 5 卓越频率对比

由表5可知，除Y向导轨频率有差异，数值模拟和模型试验的其他卓越频率频率吻合较好。Y向导轨频率差异较大可能是因为实际模型中导轨在Y向非形心受弯，而数值模拟中将导轨形心受弯考虑。

3.3 地震动响应结果对比

数值模拟考虑0.3gY向地震动输入，并对试验值和数值解的导轨加速度、应变进行对比。见图11和图12。由图11、图12可以看出，导轨绝对加速度响应、导轨应变响应的试验值和数值解在大部分测点比较吻合；在上导靴的位置差异比较大，无保持装置情况下的吻合程度要高于有保持装置。

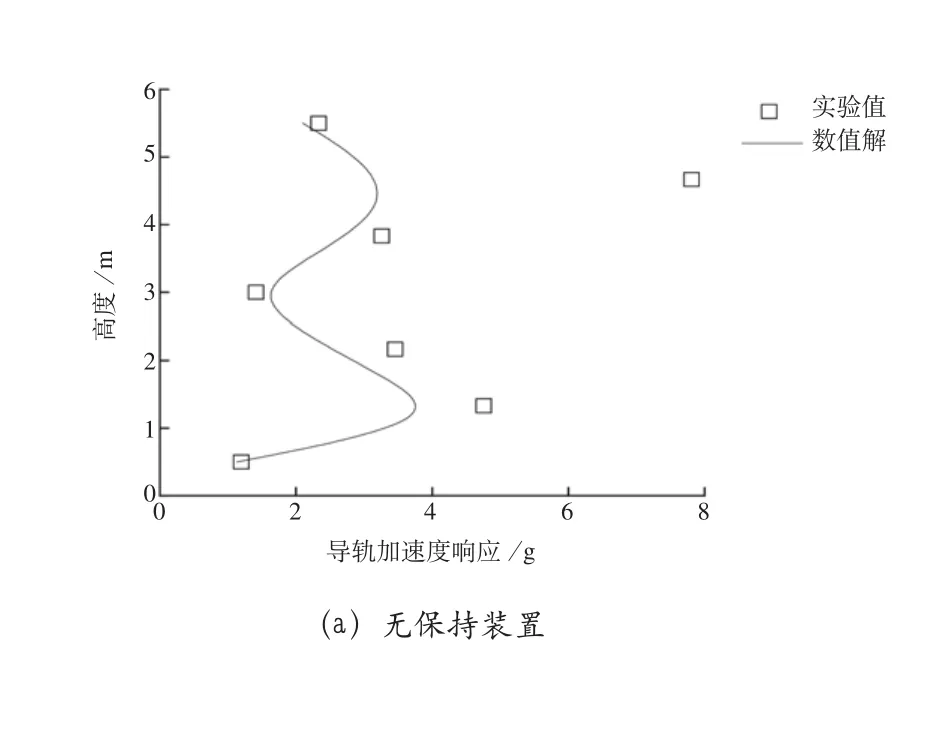
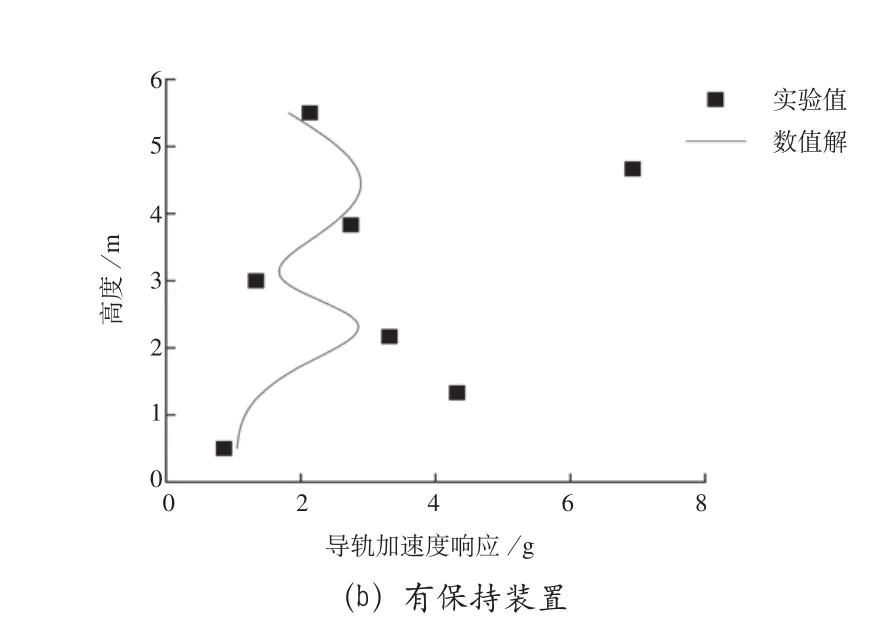
图11 应变峰值对比

图12 加速度峰值对比

4 结论

通过电梯局部对重结构的足尺动力模型试验和数值模拟，可得到以下结论：

试验模型的对重、外框架和导轨等结构在X、Y两个方向的振动周期比较接近，模型的对称性较好，前几阶模态以平动为主，试验中试验模型未出现明显扭转；保持装置的有无对结构基频没有影响。

X与Y向的动力响应有差别，加速度响应Y向明显大于X向；动应变响应X向下部较大，Y向上部较大。

加速度响应在保持装置的作用下均有减小；应变和变形响应没有因为保持装置的存在而整体减小，但最大测点峰值减小明显，且整体有均化趋势，这都说明保持装置对地震下电梯导轨的动力响应、动应变以及变形的降低有重要贡献和作用。

数值解和试验值吻合响度较好，证明了Kelvin模型在接触碰撞分析中的实用性。

[1] 卜四清. 从ISO/TR 25741浅谈电梯抗震要求[J].科技传播， 2011(09)：152-153.

[2] 崔健坤，林进展，罗海军．地震中运行电梯对重脱轨原因探讨[J]．机电工程技术，2013，42(8)：193-196.

[3] Yang T Y, Kullegowda H, Kapania R K, et al. Dynamic response analysis of elevator model[J]. Journal of structural engineering，1983，109(5)：1194-1210.

[4] Segal F, Rutenberg A, Levy R. Earthquake response of structure-elevator system[J]．Journal of structural engineering New York, N.Y., 1996，122(6)：607-616.

[5] Singh M P, Suarez L E, Rildova L. Seismic response of rail-counterweight systems in elevators[J]．Earthquake Engineering and Structural Dynamics，2002，31(2)：281-303.

[6] 吴波，李惠．高层建筑电梯平衡重体系的动力特性与地震反应分析[J]．地震工程与工程振动，1995，15(3)：88-98.

[7] 钱江，宋洋，胡俊．地震作用下电梯对重系统动力响应[J]．中国科技论文在线，2008．

[8] 朱明，张鹏．朱昌明，等．电梯轿厢和导轨耦合系统的地震响应分析[J]．地震工程与工程振动，2013，33(4)：183-188.

[9] GB/T 31095—2014 地震情况下的电梯要求[S].

[10] Jankowski R. Non-linear viscoelastic modelling of earthquake-induced structural pounding[J]．Earthquake engineering & structural dynamics，2005，34(6)：595-611.

[11] Jankowski R，Wilde K，Fujino Y．Pounding of superstructure segments in isolated elevated bridge during earthquakes[J]．Earthquake engineering & structural dynamics，1998，27(5)：487-502.

[12] 胡俊．高层建筑电梯系统水平地震响应分析[D]．上海：同济大学，2007.

Experimental Research and Analysis on Aseismic Measure of Counterweight-rail System in Elevator

Lv Fengying1Zhu Tong2Wan Hui2
(1. Hebei Fengning Pumped Storage Co., Ltd. Chengde 068350)
(2. Faculty of Infrastructure Engineering, Dalian University of Technology Dalian 116024)

During the earthquake, the derailment of counter-weight is mainly caused by excessive dynamic response of guide-rails. In order to know the difference of dynamic response of the guide-rail during the earthquake, we make the vibration experiment on a full-scale model with a counter-weight and guide-rails, we also make the numerical simulation in ANSYS. Test results show that the experiment and numerical simulation results are in good agreement; When the same direction and the same amplitude earthquake excitation, the dynamic response of the rail with keeping devices is smaller than the rail without, and the keeping device homogenize the dynamic response, all these can effectively prevent the derailment of the counter-weight during the earthquake.

Derailment of counter-weight Keeping device Full-scale model Vibration experiment Numerical simulation

X941

B

1673-257X(2016)11-0023-07

10.3969/j.issn.1673-257X.2016.11.006

吕风英(1988～)，男，硕士，从事结构抗震及健康检测工作。

2016-04-28）