热障涂层氧化层厚度对残余应力的影响*

陈宇慧 岳利文 张永海 戚俊清

(郑州轻工业学院 能源与动力工程学院)

热障涂层氧化层厚度对残余应力的影响*

陈宇慧**岳利文 张永海 戚俊清

(郑州轻工业学院 能源与动力工程学院)

对热障涂层氧化过程进行了详细的阐述，推算了氧化增厚动力曲线，采用ANSYS分别建立了不同氧化层厚度的热障涂层微观二维模型，氧化层界面形状简化为正弦形式。模拟了氧化层不同特征厚度时的应力变化，分析了不同氧化增长方向对各层残余应力的影响。结果表明：随着氧化层的增厚，粘结层波峰处σy增幅较大，易在氧化层和粘结层间发生分层。氧化层分别向TBC层、BC层以及同时向两层方向增长时，发现不同的氧化层增长方向对各层内的残余应力影响不大，可以忽略其影响。

热障涂层 残余应力 氧化动力曲线 氧化层 非线性有限元

热障涂层是把陶瓷材料沉积在金属材料的表面，提高金属材料的耐高温和抗腐蚀性能以延长使用寿命。热障涂层具有极低的热传导率、较高的热膨胀系数、抗高温、抗氧化及耐腐蚀等优良性能，应用越来越广泛。典型的热障涂层包括4层结构，分别为陶瓷涂层、粘结层、热生长氧化层和高温合金基体。当运行温度高达700°C以上时，粘结层被氧化并生成了氧化层，也就是所说的热生长氧化层(TGO) , TGO的厚度在1～10μm，存在于粘结层和陶瓷层之间[1]。热障涂层服役过程中不可避免的会生成TGO，理想的粘结层中TGO成分主要是α-Al2O3，生长缓慢并且有规则。在氧化初期，粘结层中的Al元素含量比较高，容易与从陶瓷隔热层扩散过来的O元素发生化学反应生成氧化层。随着氧化层的增厚粘结层中的Al元素含量不断下降，使得氧化层生长速度降低；同时随着氧化层不断增厚，氧化层对O元素向粘结层扩散的阻隔能力也越来越大，同样使得氧化层的增厚越来越困难。

就目前的研究来看，热障涂层的失效原因主要有：陶瓷层和粘结层的热膨胀系数不匹配所引起的热应力；热生长氧化层的生成；结构中组分的不断改变[2]。热障涂层的工作环境一般都是高温环境，而涂层过早失效的关键因素就是高温环境引起热生长氧化层的生成[3]，因此，详细研究氧化层应力状况，有助于了解涂层失效模式，合理降低残余应力水平。

1 热障涂层氧化动力学方程

氧化动力学规律是采用数学的方法，将金属氧化过程中氧化增重或氧化膜厚度的增加随时间的变化描述出来。不同的金属或同一金属在不同的环境和温度下所遵循的氧化规律不同，相对应的氧化机制也不同。氧化层的厚度对其增长有着双重的影响：一方面，氧化层的生长主要取决于氧化层分布的氧离子和金属离子，随着氧化层的增厚，氧气通过速率将降低，也就降低了金属氧化率；另一方面， 由于氧化层是致密结构，可以隔断金属和氧气的接触，从而阻止内部金属的进一步氧化[4]。

生长速率的计算公式：

ΔM/ρ=ΔV

(1)

V=s×δ

(2)

(3)

式中K——氧化层厚度增长系数；

s——初始厚度；

t——时间；

V——氧化层单位面积上增加的体积，数值上等于氧化层的厚度；

ρ——氧化层密度；

δ——单位面积。

(4)

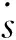
(5)

其中，rii=r11+r22+r33,通过垂直和平行于初始氧化层的轴1，轴2建立局部坐标系，这样就把一维氧化方程(4)推广到代表三维氧化法则的方程(5)。笔者在研究过程中设定r11=3，r22=r33=0，即只在TGO界面的垂直方向有增长。

根据文献[5]中的900°C氧化增重实验数据，进行进一步数据处理。其中试样加工成40mm×20mm×5mm，采用等离子技术进行喷涂。热障涂层的中间粘结层为Ni25Cr5Al0.5 Y(粉末)。分别在1、20、40、60、80、100h出炉测定试样的氧化增重，以获得氧化动力学曲线。

氧化物主要成分为Al2O3，增加的重量主要是氧原子提供的，反应方程式为：2Al3++3O2-=Al2O3，测得的增重求得氧化层增厚值，结果列于表1。

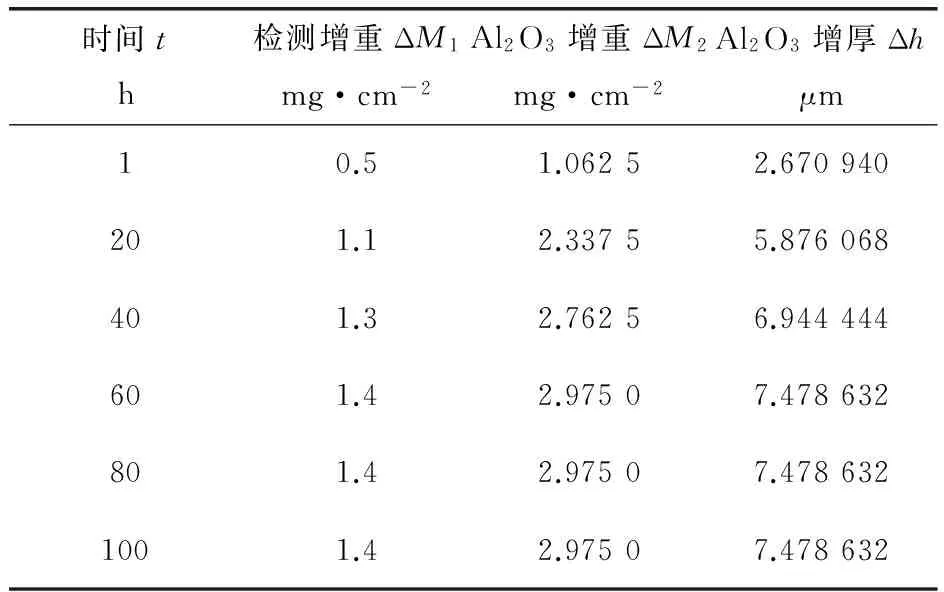
表1 氧化层增长数据

用最小二乘法拟合氧化增厚曲线s4.263=75.661t，相关系数R=0.99，表明回归拟合效果好。

2 热障涂层有限元建模

2.1几何模型和材料属性

典型的4层热障涂层系统是由合金基体(Sub)、粘结层(BC)、氧化层(TGO)和空气等离子喷涂氧化钇含部分稳定氧化锆(TBC)顶层组成，模型各层厚度分别为1 000、100、1、250μm。氧化层上下界面简化成正弦波形式[6]。为了减小计算时间，截取整体模型其中一段进行计算，截取后模型采用周期性边界条件，模型左侧采用对称约束，右侧采用多点耦合控制约束。几何模型如图1所示，采用间接热-结构耦合瞬态计算，热分析时选用二维四节点Plane55热实体单元，结构分析采用Plane182平面应变单元。不同温度下各层材料属性参考文献[7]。

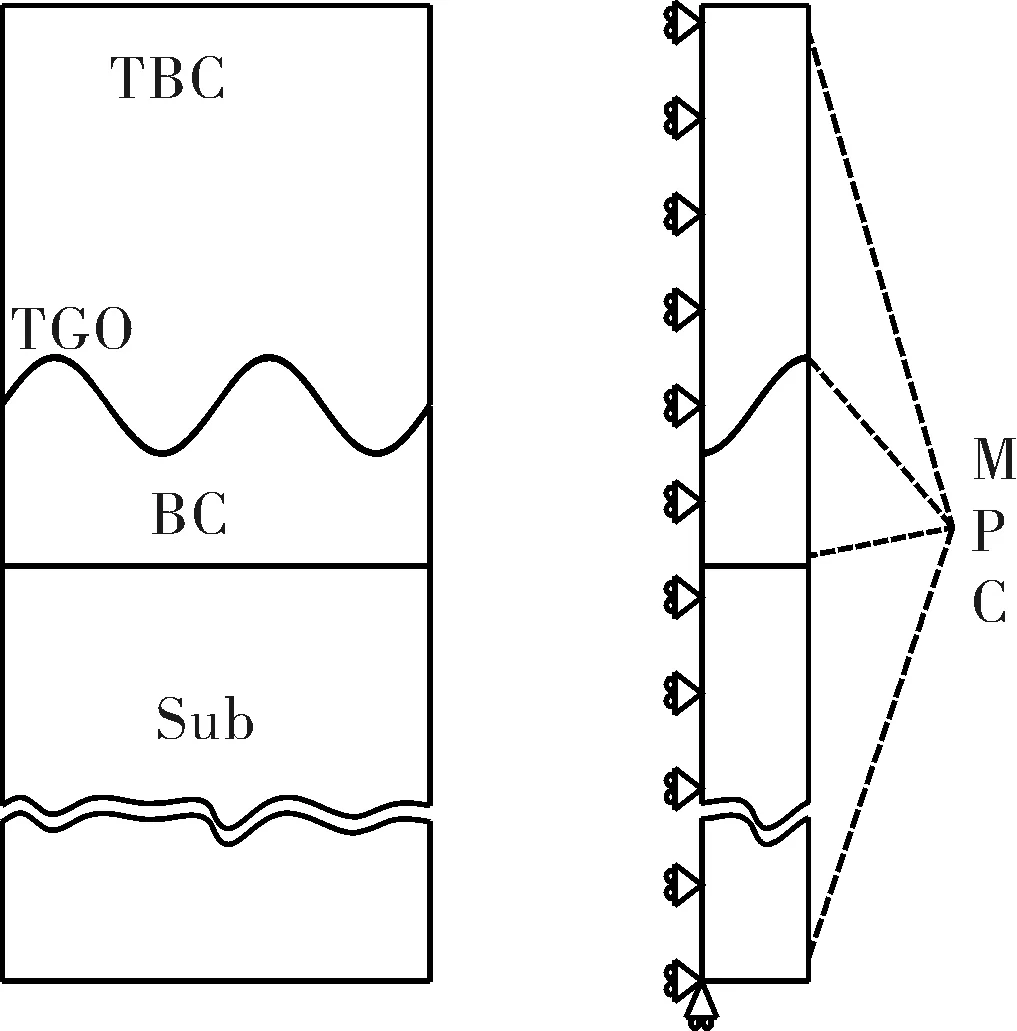
图1 TBC系统几何模型

2.2载荷和边界条件

采用热-结构间接耦合计算，其中涂层上下表面采用对流换热方式，内部依靠热传导方式进行传热。热载荷为上表面在300s内从900°C降温到室温25°C；下表面300s内由400°C同样冷却到室温，系统左右两侧绝热处理。热计算结束后进入结构计算，采用周期边界条件：涂层左侧施加X方向对称约束；涂层左下角节点固定Y方向位移；右侧采用MPC节点耦合技术，满足右侧节点具有相同的X向位移。

3 结果与讨论

3.1正弦形氧化层厚度对应力场的影响

热障涂层在服役时，氧化层会随时间增厚，但增厚到一定程度时这种行为会停止，这是由于致密的氧化层阻止了粘结层的铝离子和外界的氧离子的扩散。但随着氧化层的增厚会引起体积的增大以及各层应力的重新分布。研究表明，当氧化层的层厚增大到一定厚度时，会引发涂层的屈服与断裂，因此控制氧化层的厚度对保护热障涂层，提高热障涂层使用寿命起着重要的作用。改变氧化层厚度模型选用波长T=0.02mm，幅值A=5μm的正弦模型，氧化层厚度分别取1 、2、3、4、5、6、7μm。完成计算后提取氧化层与粘结层的各个方向应力分量云图，如图2所示。

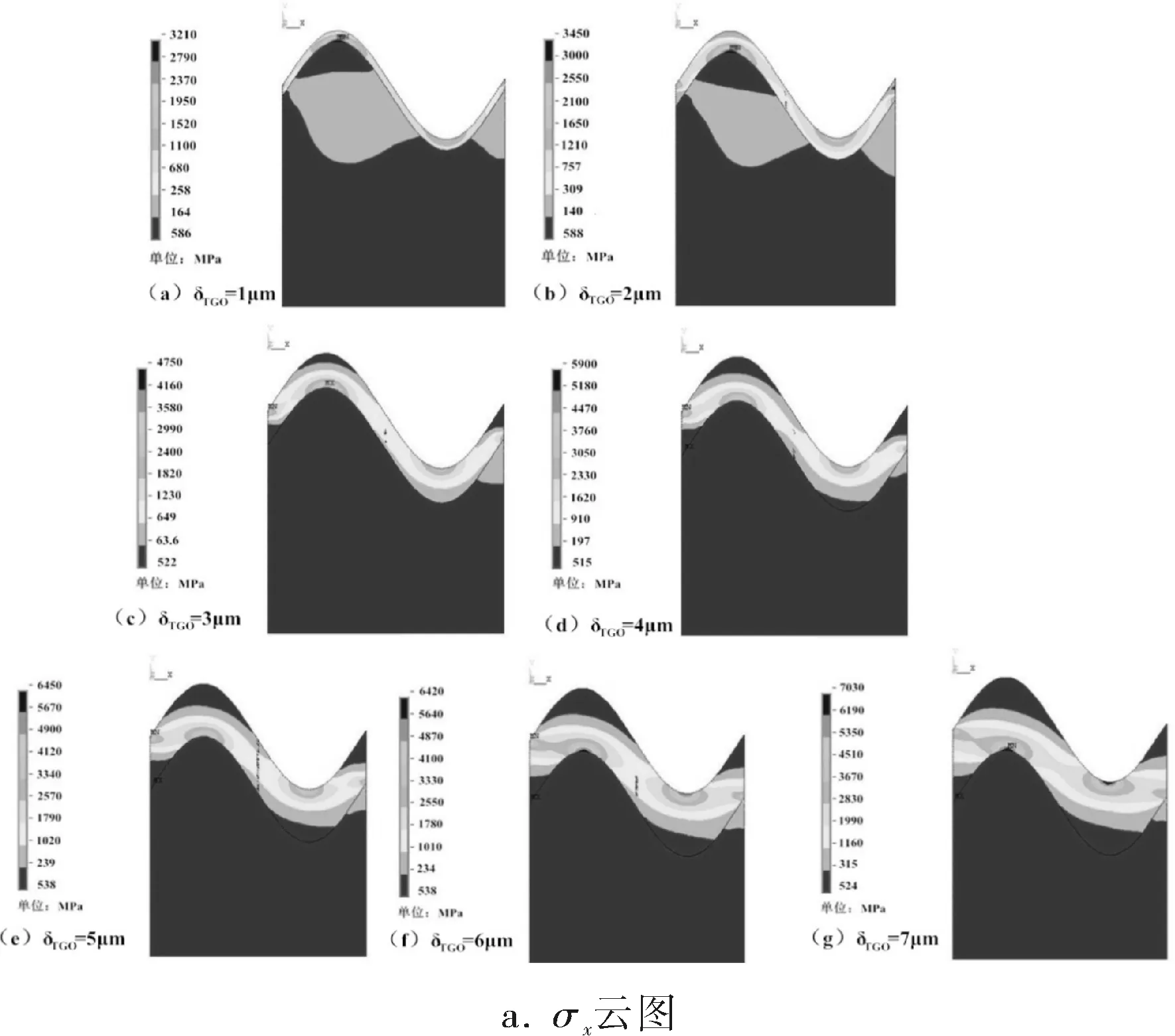
图2 氧化层和粘结层应力云图

热障涂层系统中陶瓷层应力水平较低，因此本文主要给出氧化层和粘结层应力云图。观察图2a发现，当氧化层厚度较小时，氧化层内σx为压应力，随着氧化层的增厚，氧化层内波峰波谷区域由压应力变为拉应力。从图2b中可以看出，涂层系统内最大σy出现在粘结层波峰区域，随着氧化层厚度的增加σy也增大，且高应力区域也不断扩大。从图2c可以看出最大τxy出现在氧化层的拐点区域，随着氧化层的增厚，最大应力向氧化层波峰波谷移动。

氧化层和粘结层波峰位置处σy随着氧化层厚度的变化规律，得到粘结层的应力值要高于氧化层内的应力；随着氧化层厚度增加，波峰处σy也随之增加，其中氧化层波峰处σy由417MPa增加到580MPa，粘结层波峰处σy由621MPa增加到942MPa。由于此处的拉应力σy较大且粘结层和氧化层间有较大的应力阶跃，所以此处易发生脱层失效。

3.2正弦形氧化层增长模式对应力场影响

氧化层的增长可分为3种情况：仅金属离子向外扩散，在氧化物/气体界面上进行反应；仅氧向内扩散，在金属/氧化物界面上进行反应；金属离子和氧两个方向相向扩散，它们在氧化膜中相遇并进行反应。

针对上述3种传质方式进行模拟，保持涂层系统的厚度不变，随着氧化层的增厚，第一组数据为氧化层下表面固定，上表面向TBC层方向增长；第二组数据为固定氧化层的上表面保持不变，下表面向BC层方向增长；第三组数据为氧化层中心线位置固定，上下表面分别向TBC和BC层方向增长各半。计算结果表明，氧化层和粘结层内应力水平远远高于陶瓷层内应力，因此此处不对陶瓷层应力进行分析。随着氧化层的增厚，提取3种不同增长方式波峰处σx、σy以及拐点处最大τxy计算结果。其中氧化层内τxy最大，其次粘结层σy，TGO层内波峰处σx随着氧化层厚度的增加先增加后减小；而BC层内波峰处σx则随着氧化层厚度的增加而减小。TGO层和BC层内的σy随着氧化层厚度的增加呈增加趋势。TGO层内最大τxy随着氧化层的增厚而增大，且增幅较大； BC层最大τxy随着氧化层厚度的增加，先增大后减小。可以看出3种增长方式对应力的影响很小，3组数据基本重合，总体来说可认为层内应力变化与增长方式无关。

4 结论

4.1根据增重实验进行推导计算，得到热障涂层氧化层增厚动力曲线，并得到氧化层厚度大约在7μm左右。

4.2σx随着氧化层的增厚，氧化层内波峰波谷区域由压应力变为拉应力；涂层系统内最大σy出现在粘结层波峰区域，且随氧化层的增厚而增大；涂层系统内最大τxy出现在氧化层的拐点区域，随着氧化层的增厚，最大τxy向氧化层波峰波谷移动。

4.3氧化层分别向TBC层、BC层以及同时向两层方向增长时，得到的残余应力数据基本一致，发现不同的氧化层增长方向对各层内的残余应力影响很小，可以忽略。

[1] 管恒荣, 李美姮, 孙晓峰, 等. 高温合金热障涂层的氧化和失效研究[J]. 金属学报, 2002, 38(11): 1133～1140.

[2] Padture N P, Gell M, Jordan E H. Thermal Barrier Coatings for Gas-Turbine Engine Applications [J].Science, 2002,296(5566):280～284 .

[3] Madhwal M, Jordan E H, Gell M.Failure Mechanisms of Dense Vertically-Crackedthermal Barrier Coatings[J].Materials Science and Engineering A,2004,384(1/2):151～161.

[4] 周益春,刘奇星,杨丽,等. 热障涂层的破坏机理与寿命预测[J]. 固体力学学报, 2010, 31(5): 504～531.

[5] 任鑫.等离子喷涂热障涂层的高温氧化行为研究[J].热加工工艺，2009，38(16):101～103．

[6] Hsueh C H, Fuller J E R. Residual Stresses in Thermal Barrier Coatings: Effects of Interface Asperity Curvature/Height and Oxide Thickness[J].Materials Science & Engineering: A,2000,283(1):46～55.

[7] Ranjbar-Far M, Absi J, Shahidi S, et al. Impact of the Non-Homogenous Temperature Distribution and the Coatings Process Modeling on the Thermal Barrier Coatings System[J].Materials & Design, 2011,32(2):728～735.

OxideLayerThicknessEffectofThermalBarrierCoatingonResidualStress

CHEN Yu-hui, YUE Li-wen, ZHANG Yong-hai, QI Jun-qing

(SchoolofEnergyandPowerEngineering,ZhengzhouUniversityofLightIndustry,Zhengzhou450002，China)

The oxidation process of thermal barrier coating was expounded and the oxidation kinetics curve was deduced; applying ANSYS to establish a micro two-dimensional model for oxide layer’s different thickness of the thermal barrier coating where the interface shape of oxide layer can be simplified to a sine form. Simulating stress variation at oxide layer’s different characteristic thickness and analyzing different oxide growth directions’ influence on the residual stress of various oxide layers show that, with the thickening of the oxide layer,σyat the top of bonding layer becomes bigger and the delamination occurs between oxide layer and bonding layer; when the oxide layer increases towards TBC layer and BC layer respectively or both layers simultaneously, the oxide growth direction can influence the residual stress slightly and it can be ignored.

thermal barrier coatings, residual stress, oxidation kinetics curve, oxide layer, nonlinear finite element

*福建省质量技术监督局科技计划项目(FJQI2014053)，郑州轻工业学院博士启动基金项目(2014BSJJ076)。

**陈宇慧，女，1986年2月生，讲师。河南省郑州市，450002。

TG174.4

A

0254-6094(2016)03-0397-04

2015-10-08)