矩形螺旋通道气液两相流流动和传热特性数值研究*

周云龙 张 超 张立彦 孙 博

(东北电力大学能源与动力工程学院)

矩形螺旋通道气液两相流流动和传热特性数值研究*

周云龙**张 超 张立彦 孙 博

(东北电力大学能源与动力工程学院)

采用Eulerian模型对矩形截面螺旋通道内气液两相流进行数值模拟，研究了螺旋通道内不同轴向位置气液两相流动的速度分布、相分布和温度分布特性，并分析无量纲螺距对速度分布、温度分布、单位长度压降和换热系数的影响。对水动力模型数值结果与实验结果、传热模型数值结果与实验关联式进行对比，结果表明：在一定范围内，无量纲螺距的增加使得速度场、温度场变化梯度增大，同时壁面换热系数稍有增大；超过无量纲螺距临界值，速度场和温度场的变化梯度随无量纲螺距的增加而减小；随着无量纲螺距的增加，单位长度平均压降稍有增加，并且增加的幅度逐渐减小；无量纲螺距对相分布特性几乎无影响；随着入口截面含气率的增加，单位长度平均压降和换热效果提高。

矩形螺旋通道 两相流 流动特性 传热特性 数值模拟 计算流体动力学

螺旋通道是一种典型的空间曲线通道，因其结构紧凑、传热效率较高，在动力装置、化工机械及核电设备等领域广泛应用。由于矩形截面螺旋通道加工技术比圆形截面螺旋通道加工技术简单，现已逐渐受到人们的重视。矩形截面螺旋通道主要应用于可实现锅炉余热回收利用的膨胀动力装置的单螺杆膨胀机中。单螺杆膨胀机适合于烟气余热回收系统[1]，而影响其效率的主要因素就是复杂三维矩形螺旋通道内多组分、多相流的流动结构。想要有效提高单螺杆膨胀机的效率，实现高质量余热回收，就要充分了解螺旋槽道内流体的流动形态。

目前，研究人员对圆形截面螺旋通道内两相流动已进行了大量的理论、实验和数值研究。Murai Y等实验研究了螺旋管内气液两相流的流动特性，提出离心加速度对于气液两相流动结构有重要影响，并分析了截面含气率对压力波动的作用[2]。Vashith S和Nigam K D P完成了圆形截面螺旋通道内气液两相流的流动分布和界面现象的研究[3]。Jayakumar J S等利用数值方法完成了立式螺旋管内气液两相流热力、水动力学特性的研究，得到了不同螺旋管道结构参数下的流动和传热规律[4]。赵立新等数值分析了螺旋管内油水两相的分离特性，得到了螺旋管的回转半径和入口流速是影响气液两相体积分数分布的主要因素的结论[5，6]。

对于矩形截面螺旋通道单相流体的流动和传热特性研究也取得了一些成果。文献[7～9]研究了矩形截面螺旋通道内二次流现象。文献[10，11]利用数值方法完成矩形截面螺旋管道内流体粘性流动的研究，分析了离心力和科氏力共同作用下的二次流动、速度和温度分布随各参数的变化情况。

矩形截面螺旋通道内气液两相流动特性的研究相对较少，刘献飞等通过实验方法对矩形螺旋通道内弹状流的流动特性进行研究，发现流动特性会随着螺旋周角的变化而变化[12]。周云龙和张立彦利用数值方法研究了矩形截面立式螺旋管内的气液两相流流型转换，并绘制流型图[13，14]。Xia G D等通过数值模拟方法对不同结构参数、入口含液率等因素对矩形螺旋管内气液两相流摩擦压降的影响进行了研究[15，16]。

目前，针对矩形截面螺旋通道气液两相流流型和压降特性都有相应的探索，但对于矩形截面螺旋通道的特征尺寸对气液两相流的速度分布、相分布特性等缺乏深入研究，且矩形截面螺旋通道气液两相流传热特性的研究少有报道。

螺旋型通道自身的复杂三维螺旋结构对通道内流体流动特性的影响一直是科研工作中值得关注的问题，较好地设计螺旋型通道特征尺寸，是强化气液两相传热、提高换热效率的基础。笔者主要针对矩形截面螺旋通道内的气液两相流动进行研究，了解螺旋通道内气液两相流动特性和传热特性机理，通过改变不同的无量纲螺距、入口截面含气率系统分析螺旋通道内不同轴向位置气液两相流动的速度分布、相分布和温度分布特性，并得到螺旋通道特征尺寸无量纲螺距对流动和传热特性的影响规律。

1 数值方法与结构参数

1.1结构参数

图1给出了典型的卧式矩形横截面螺旋通道结构示意图。其结构参数包括截面边长a、b(文中a=0.024m，b=0.022m)，螺旋曲率半径R、螺距P，当量直径d=2ab/(a+b)，螺旋直径Dc=2R，无量纲螺距H=P/2πR，曲率λ=R/Dc，雷诺数Re=ρvd/μ(ρ是流体的密度，μ是流体的动力粘度)，离心加速度为v2/R，螺旋通道内临界雷诺数决定通道内流体流动形态，临界雷诺数Recri=2100(1+12λ0.5)[17]。矩形截面螺旋通道模型包括水平入口直管段和两圈螺旋通道(图2)。Bolinder C J和Bengt Sundén提出了在2.5倍螺距处，流体流动已经充分发展[18]。为保证流动充分发展，笔者所采用的入口直管段长度取5倍螺距长度。不同螺旋周角用θ表示，θ=0°表示螺旋通道起始点，θ=360°表示螺旋通道旋转一周，θ=720°表示螺旋通道出口。

图1 卧式矩形横截面螺旋通道结构示意图

图2 矩形横截面螺旋通道计算域示意图

1.2数学模型

笔者采用Eulerian多相流模型进行分析，体积分数代表每一相所占据的空间，并且每相均满足质量和动量守恒定律：

(1)

这里，Vk表示k相的体积，每个控制体内所有相的体积分数和为1。将气相体积分数记为αg，液相体积分数记为αl，则αg+αl=1。

连续性方程为：

(2)

动量守恒方程为：

(3)

式中Fk——外部体积力；

Flift，k——升力；

Fvm，k——虚拟质量力；

Rpq——相间作用力；

upq——两相滑移速度；

τk——液体间的剪应力张量。

能量守恒方程为：

(4)

式中hk——k相的焓值；

hpq——界面焓值；

pk——k相的压力；

qk——热通量；

Qpq——相间热量交换。

1.3计算域与边界条件

计算域采用非稳态计算，流道内混输流体为不可压缩的空气-水两相流体，气泡直径为0.1mm。对于不可压缩流体，压力的改变对物性影响较小，然而温度对物性的影响较大，不可忽略。笔者利用Matlab对温度为273～373K的空气、水的物性进行线性拟合，得到在标准大气压力(101.325kPa)下空气和水的物性参数关于温度的关系式(表1)。

表1 干空气、饱和水的物性参数关于温度的关系式

文中涉及到的算例中，雷诺数均大于临界值，流动为紊流流动。入口为恒定速度入口，给定各相的折算速度和来流的湍流强度，气相折算速度vg、液相折算速度vl和入口截面含气率α依情况而定。出口压强为一个大气压，全流道与流体相接处的壁面采用无滑移壁面条件。有传热情况下，入口空气、水温度均恒为360K，壁面温度均恒为300K，且不考虑相间传热。

1.4离散和求解算法

利用Pro/E建立物理模型，导入到ICEM CFD划分结构化网格。基于Fluent商业软件平台，利用有限体积法进行三维数值模拟。考虑到Realizablek-ε模型[19]对具有二次流的复杂流动的计算具有显著优势，所以湍流模型采用Realizablek-ε模型。离散梯度采用Green-Gauss Cell Based方法离散，动量和体积分数采用QUICK差分格式，流场采用压力-速度耦合的Phase coupled SIMPLE(PC-SIMPLE)格式求解。湍动能，湍流扩散率采用Power Law格式。设置合理的时间步长、松弛因子、最大迭代步数以保证收敛。

1.5网格无关性讨论

针对表2中No.3结构参数的矩形螺旋通道模型，vg、vl均为2.5m/s，α为0.2工况下，进行网格无关性验证。分别做了网格平均密度为110 000 000、150 000 000、220 000 000、330 000 000个/m3的4组网格，并沿着管程设置12个监测点，监测其静压p变化。网格无关性验证如图3所示，结果显示，网格平均密度在220 000 000个/m3以上时，变化幅度在2%以内。继续增加网格数对结果影响不大，但计算时间与资源增加，所以采用网格平均密度为220 000 000个/m3的网格进行计算。

表2 矩形螺旋通道结构参数

图3 网格无关性验证

2 模拟结果与讨论

2.1模型验证

2.1.1水动力模型验证

为了验证本数值模型的正确性，在本课题组矩形螺旋通道气、水两相流实验台上对本数值模型做了相应的实验验证。实验在常温条件下进行，通过改变气液两相的流量分配，获得不同的实验段压降值，实验的压降通过实验段两测点上压力差获得。压力参数范围为0.1～0.3MPa；空气的折算速度范围为0.2～20.0m/s；水的折算速度范围为0.04～2.70m/s。数值模拟的物理模型与实验段完全相同，且在相应位置处取得两点的压差值，实验段特征尺寸见表2中No.1结构参数。

通过定量分析数值计算的压降与实验获得的压降值进行对比。图4给出了实验模型下，25组不同气液两相入口速度的压降模拟值与实验值的压降数据对比，可以看出模型计算值实验值基本吻合，两者的平均误差在20%左右。误差来源是实验本身测量误差和数值模拟的不确定性，这基本保证了水动力模型的正确性。

图4 模型计算值与实验值对比

2.1.2传热模型验证

笔者针对螺旋通道内单相水在雷诺数Re为6 000～62 000范围内的对流换热进行模拟。模拟结果分别与修正的Dittus-Boelter[20]公式预测值进行对比，与Mori Y和Nakayama W[21]半理论半经验方法得到的恒壁温边界条件下，管内充分发展紊流换热经验公式预测值进行对比。图5显示数值结果与两种模型预测值相比整体偏小，本文预测值与Dittus-Boelter公式预测值和Mori Y和Nakayama W公式预测值最大误差为20.75%。以上分析证明了该模拟方法和结果在可接受的范围内。

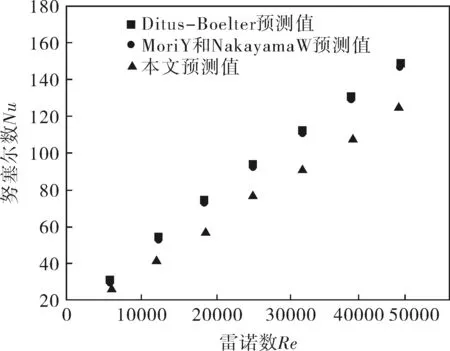
图5 换热系数对比

2.2矩形截面螺旋通道气液两相流流动特性研究

2.2.1无量纲螺距对速度场的影响

图6为表2中No.2～5结构参数下，vg、vl均为2.5m/s，α为0.2的不同无量纲螺距、不同螺旋周角下径向截面的液相速度场分布。图中截面上部代表螺旋通道外壁面(远离旋转中心轴的壁面)，下部代表螺旋通道内壁面(靠近旋转中心轴线的壁面)。不同无量纲螺距下液相速度场的形成过程相似。由于流动方向不断变化且受通道截面的影响，使得速度场随螺旋周角不断变化，速度最大值逐渐集中于通道轴线外侧。在θ=270°，螺旋通道内壁面两个角区向外开始形成两个漩涡，θ=360°，速度场内壁面附近形成了稳定的漩涡，流动形态基本不变。

随着螺旋周角的增加，由于流体受到离心力作用，使得中心流体在横截面切向方向上产生了速度分量，与边壁流体存在动量差，流动偏向外壁面[7]。在扭转力、科氏力和离心力的共同作用下，最大值逐渐集中于壁面外侧。

随着流动的发展，内壁面两个角区沿壁面向外出现的相似漩涡，这是第一类普朗特二次流和第二类普朗特二次流[22]共同作用的结果。由于靠近外壁处流体速度较大、压力较低，截面上压力差使内侧流体向外壁面流动，碰到壁面后，速度减小至零，而后反向流动，形成二次流[8]。

对比不同无量纲螺距、不同螺旋周角下的速度场分布，可以看出：螺旋周角一定时，速度梯度变化幅度随着无量纲螺距的增加而增大，当无量纲螺距增加到0.125以后，速度梯度变化幅度又随着无量纲螺距的增加而减小。并且无量纲螺距从0.057增加到0.125，速度场更块地达到稳定。这是由于无量纲螺距的增大，使得扭转力增大，通道内两相流的紊流强度增强，速度场更快达到稳定。在无量纲螺距增加到0.125以后，随着无量纲螺距的增加，反而削弱了速度场的变化幅度。这可能是由于在无量纲螺距为0.125～0.159之间存在一个临界值，使得螺旋通道内流体所受的离心力、科氏力、扭转力的耦合作用发生改变，从而改变速度场的变化的趋势。

2.2.2无量纲螺距对相分布特性的影响

图7给出了表2中No.3结构参数下，vg、vl均为2.5m/s，α为0.2的不同螺旋周角气相分布。随着转角的增加，气相区域逐渐向通道内侧壁面移动。在螺旋周角0～180°的下降段，气相分布变化明显。旋转一周后，气相主要集中在螺旋通道内壁面中心。

图7 No.3结构参数下气相分布

这是由于气相在流动过程中受到壁面的扭转力、液相紊流应力、离心力、浮升力与科氏力的耦合作用，气相密度远小于液相密度，液相相对于气相产生径向外的偏移趋势，液相逐渐向通道外壁面侧移动，使得气相聚集在内侧壁面。

对No.2～5结构参数下气相分布进行了分析，随着无量纲螺距的增加，相同螺旋周角下的气相分布变化并不明显，这是由于在离心力和扭转力共同作用下，扭转力的作用远小于离心力的作用，无量纲螺距的改变造成的影响并不明显。

2.2.3无量纲螺距和入口含气率对压降的影响

图8给出了表2中No.2～5结构参数下，vg、vl均为2.5m/s，α分别为0.15、0.20、0.25、0.30的单位长度平均压降。随着无量纲螺距的增加，单位长度平均压降稍有增大，且无量纲螺距增加到0.125以后，单位长度压降增加的幅度极小。单位长度压降增加原因是扭转力和二次流作用，使得流动更加剧烈，损失增大，导致单位长度的压降增大。

图8 不同无量纲螺距的单位长度平均压降

随着入口截面含气率增加，单位长度平均压降明显降低，这是由于气相的密度远小于液相密度，气相体积份额增加，相同的折算速度下，单位时间内流过的两相流体质量降低，单位长度平均压降也随之减小。对比可以看出，压降随入口截面含气率的变化远大于随无量纲螺距的变化。可知无量纲螺距对压降的作用小于入口截面含气率的作用。考虑螺旋通道内气液两相压降的影响因素时，无量纲螺距的影响可忽略，但是入口截面含气率的影响不可忽略。相同的结论在文献[23]可见。

2.3矩形截面螺旋通道气液两相流传热特性研究

2.3.1无量纲螺距对温度场的影响

图9给出了表2中No.2～5结构参数下，vg、vl均为2.5m/s，α为0.2的不同无量纲螺距、不同螺旋周角下径向截面的气相和液相温度场分布。壁面温度低于主流温度，随着流动的发展两相流体被逐渐冷却。在螺旋周角0～30°之间，4个边壁的冷却效果基本相同，θ=30°以后，气相温度最大值逐渐集中在外壁面附近。直到θ=360°气相温度场形成明显的3个区域，靠近通道外侧壁面为高温区(340～350K)，管道中心为中温区(321～340K)，靠近通道内侧壁面为低温区(300～321K)。在θ=360°以后，径向截面上温度场分布基本不变，只是随着壁面的冷却，温度整体降低。液相温度场与气相温度场相类似的趋势，但是由于液相的比热容相对气相较大，温度变化幅度相对气相温度变化幅度较小。

图9 不同无量纲螺距、不同螺旋周角下径向截面的温度场分布

随着无量纲螺距的增加，气相、液相的温度变化幅度增大，这是由于扭转力作用增强，使得速度变化幅度增大，从而影响温度场的分布。当无量纲螺距增加到0.125时，温度场的变化梯度反而减小。原因可能与无量纲螺距对速度场分布的作用相同。

2.3.2无量纲螺距和入口含气率对换热系数的影响

图10给出了表2中No.2～5结构参数下，vg、vl均为2.5m/s，α分别为0.15、0.20、0.25、0.30的壁面平均换热系数。随着无量纲螺距的增加，壁面平均换热系数增大，这是由于无量纲螺距增大，扭转力使得湍动能增加，换热效果增强。无量纲螺距增加到0.125以后，换热系数反而减小。随着入口截面含气率的增加，壁面平均换热系数呈线性递减趋势。原因是气相份额增加，气相的换热系数较小，总平均换热系数减小。相同体积，液相体积分数减少，换热量相对减少，使得换热系数降低。

图10 不同无量纲螺距的壁面平均换热系数

3 结论

3.1基于Eulerian多相流模型建立了不同无量纲螺距下矩形螺旋通道气液两相流动的三维非稳态数学模型，通过实验和传热关联式的验证，保证了数值模型和结果的正确性。螺旋周角的增加，使速度最大值逐渐集中在通道外壁面附近。在第一类和第二类普朗特二次流耦合作用下，内壁面两个角区形成两个对称漩涡，气相逐渐集中在通道内壁面。

3.2无量纲螺距对相分布特性作用不大。

3.3气液两相温度场分布与速度场分布趋势基本相同。气相温度场变化较液相温度场变化明显。

3.4入口截面含气率与单位长度平均压降和平均壁面换热系数成反比。在一定范围内，螺距的增加，单位长度平均压降和平均壁面换热系数稍有增大。

3.5可能存在一个无量纲螺距的临界值，使得无量纲螺距的作用在这个临界值上对速度场分布，气相和液相温度场分布，壁面换热系数的影响趋势发生改变。这还需要后续的研究来证明。

[1] Wang W，Wu Y T， Xia G D，et al.Experimental Study on the Performance of the Single Screw Expander Prototypes by Optimizing Configuration[J].Energy，2013，62：397～384．

[2] Murai Y，Oiwa H，Sasaki T，et al.Backlight Imaging Tomography for Gas-Liquid Two-phase Flow in a Helically Coiled Tube[J]. Measurement Science and Technology，2005，16(7)：1459～1468．

[3] Vashisth S，Nigam K D P.Prediction of Flow Profiles and Interfacial Phenomena for Two-phase Flow in Coiled Tubes[J].Chemical Engineering and Processing：Process Intensification，2009，48(1)：452～463．

[4] Jayakumar J S，Mahajani S M，Mandal J C，et al.Thermal Hydraulic Characteristics of Air-Water Two-phase Flows in Helical Pipes[J].Chemical Engineering Research and Design，2010，88(4)：501～512．

[5] 赵立新，华正荣，朱宝军，等.脱油型螺旋管油水分离器的数值模拟[J].化工机械，2008，35(6)：345～349.

[6] 赵立新，华正荣，关凤珠，等.螺旋管分离器流场分布及影响规律分析[J].化工机械，2010，37(5)：592～595，649．

[7] 马源，曹文瑾，林梅.矩形截面螺旋通道内的二次流流场特性[J].西安交通大学学报，2014，48(8)：122～127．

[8] 张丽，邢彦伟，吴剑华.矩形截面螺旋通道内流体的流动特性[J].化工学报，2010，61(5)：1089～1096．

[9] Jonas Bolinder C， Sundén B.Numerical Prediction of Laminar Flow and Forced Convective Heat Transfer in a Helical Square Duct with a Finite Pitch[J].International journal of heat and mass transfer，1996，39(15)：3101～3115．

[10] 张金锁，章本照，陈倩.旋转矩形截面弯管内流动特性的研究[J].空气动力学学报，2001，19(2)：135～147．

[11] 陈华军，沈新荣，苏霄燕，等.旋转矩形截面螺旋管内对流传热特性的研究[J].浙江大学学报(工学版)，2003，37(4)：69～73．

[12] 刘献飞，夏国栋，杨光.矩形截面螺旋通道内弹状流的流动特性[J].化工学报，2014，65(11)：4231～4237．

[13] 周云龙，张立彦.矩形截面螺旋管内气液两相流型转换数值模拟[J].化工学报，2014，65(12)：4767～4774．

[14] 周云龙，张立彦.方形截面螺旋管内气液两相流动特性数值研究[J].化工机械，2015，42(1)：85～92.

[15] Xia G D，Liu X F，Zhai Y L，et al.Single-phase and Two-phase Flows through Helical Rectangular Channels in Single Screw Expander Prototype[J].Journal of Hydrodynamics，Ser．B，2014，26(1)：114～121．

[16] Xia G D，Liu X F.An Investigation of Two-phase Flow Pressure Drop in Helical Rectangular Channel[J].International Communications in Heat and Mass Transfer，2014，54：33～41．

[17] 邢云绯，仲峰泉，张新宇.矩形横截面螺旋管湍流流动与传热特性的数值研究[J].航空学报，2013，34(6)：1269～1276．

[18] Bolinder C J，Bengt Sundén.Flow Visualization and LDV Measurements of Laminar Flow in a Helical Square Ducts with Finite Pitch[J].Experimental Thermal and Fluid Science，1995，11(4)：348～363．

[19] Shih T H，Liou W W，Shabbir A，et al.A Newk-εEddy Viscosity Model for High Reynolds Number Turbulent Flows[J].Computers & Fluids，1995，24(3)：227～238．

[20] (苏)洛克申，著，北京锅炉厂设计科，译.锅炉机组热力计算标准方法[M].北京：机械工业出版社，1976：47～75．

[21] Mori Y，Nakayama W.Study on Forced Convective Heat Transfer in Curved Pipes：(3rd Report，Theoretical Analysis Under the Condition of Uniform Wall Temperature and Practical Formulae)[J].International Journal of Heat and Mass Transfer，1967，10(5)：681～695．

[22] 郭亚军，毕勤成，何永清.正方形截面直通道内二次流现象的实验研究[J].西安交通大学学报，2009，43(7)：83～87．

[23] Liu X F，Xia G D，Zhai Y L，et al.Numerical Analysis of the Two-phase Pressure Drop and Liquid Distribution in Single-Screw Expander Prototype[J].Chinese Science Bulletin，2014，59(33)：4388～4396．

NumericalStudyofFlowandHeatTransferCharacteristicsofGas-LiquidFlowinRectangularSpiralChannel

ZHOU Yun-long, ZHANG Chao, ZHANG Li-yan, SUN Bo

(CollegeofEnergyandPowerEngineering,NortheastDianliUniversity,Jilin132012,China)

The Eulerian model was adopted to simulate gas-liquid flow within rectangular spiral channel; and the gas-liquid flow’s velocity distribution, phase distribution and temperature distribution in different axial positions of the spiral channel were discussed, including the non-dimensional torque’s effect on the velocity distribution and temperature distribution, the unit length pressure drop and the heat transfer coefficient. Comparing numerical results with experimental results of hydrodynamic model and the numerical result of heat transfer with the experimental correlation prove reliability of the simulation results. The results show that in a certain range, the torque’s increase can make variation gradient of the velocity field and temperature field increased, including the heat transfer coefficient of the wall slightly; however, when the torque’s critical value is exceeded, the variation gradient of velocity field and temperature field become decreased with the increase of the torque; as the torque increases, the average pressure drop per unit length becomes increased slightly and the this increase extent would diminish gradually; the torque has no obvious influence on the phase distribution characteristics; this increases inlet void fraction and improves pressure drop of the per unit length and the heat transfer effect greatly.

rectangular spiral channel, gas-liquid flow, flow characteristic, heat-transfer character, numerical simulation, CFD

*国家自然科学基金项目(51276033)，东北电力大学研究生创新基金项目。

**周云龙，男，1960年2月生，教授。吉林省吉林市，132012。

TQ022.4

A

0254-6094(2016)03-0357-08

2015-05-08，

2015-05-25)