壳单元和实体单元在矩形压力蒸汽灭菌器有限元分析中的应用

卢艳玲 董金善 朱星榜 姚 扬 赵 宁

(南京工业大学机械与动力工程学院)

壳单元和实体单元在矩形压力蒸汽灭菌器有限元分析中的应用

卢艳玲*董金善 朱星榜 姚 扬 赵 宁

(南京工业大学机械与动力工程学院)

介绍了壳单元与实体单元的线性化处理方法与安全评定方法，给出了矩形压力蒸汽灭菌器的结构参数。采用实体单元与体-壳单元对矩形压力蒸汽灭菌器进行有限元分析，结果表明：二者均满足结构强度要求，且壳单元与实体单元相比，最大TRSECA应力强度和应力分布相似，局部薄膜应力的应力强度较小，而薄膜加弯曲应力的应力强度较大，其中局部薄膜应力的应力强度最大相对误差为9.5%，薄膜加弯曲应力的应力强度最大相对误差为8.1%，均在精度允许范围内。

矩形压力蒸汽灭菌器 有限元分析 实体单元 壳单元

压力蒸汽灭菌器具有蒸汽制取简单、对环境无污染、灭菌速度快、效果好及适用范围广等优点[1]，广泛应用于化工、医疗、制药及餐饮等领域。根据灭菌室截面形状的不同，可分为圆形截面和矩形截面压力蒸汽灭菌器。圆形截面容器在相关标准中有详细的介绍与分析，并总结了简单的工程应用公式；矩形截面容器容易安装，占地面积小，具有较高的空间利用率和传热率，因此它在大型压力蒸汽灭菌器中的应用更加广泛[2]，但因其结构与受力的复杂性，难以采用一般的理论公式进行设计与评定。

随着计算机辅助设计技术的快速发展，有限元法在压力容器分析设计中的应用越来越广泛。通过有限元法对矩形压力蒸汽灭菌器进行分析能够明确观察到容器各个位置的应力分布状态，并根据相关标准对它进行安全评定。然而，对结构复杂的大型薄壁设备进行整体结构应力分析时，在建立其有限元模型时，若全部采用实体单元，则会给建模带来困难，使有限元的单元和节点个数过多，造成计算机资源消耗过大、成本过高；若对复杂压力容器合理采用壳单元替代实体单元[3～6]，对结构不连续处采用实体单元建立模型，

则可以有效减少单元和节点个数，降低计算成本，同时可以得到较为可靠的计算结果。虽然基于壳体理论的沿壁厚方向的直法线假设对壳单元的计算结果无需进行线性化处理，Ansys程序可直接输出壳单元上下表面和中面上的应力分布(上下表面上的应力为薄膜加弯曲应力，中面上的应力为薄膜应力)，但此结果与实体单元得出的结果是否具有可比性，仍是个值得探讨的问题。为此，笔者以1.2m3单层矩形压力蒸汽灭菌器为例，分别建立实体模型与体-壳装配模型，对比分析两种模型下的应力分布、应力分类和应力强度并进行灭菌器的安全评定。

1 线性化处理方法与安全评定方法

1.1 壳单元线性化处理方法

采用二维壳单元对结构进行有限元分析时，基于板壳理论的壳单元可以输出节点中层、底层、顶层的各向应力分量，则薄膜应力和弯曲应力的计算式为[7]：

其中，σt、σb、σm分别为壳体顶层、底层、中层的应力张量，σij,m、σij,b分别为评定点的薄膜应力张量和弯曲应力张量。由此可以计算评定点的薄膜应力和薄膜加弯曲应力的应力强度或相当应力。

1.2 实体单元线性化处理方法

采用三维实体单元对结构进行有限元分析时，基于应力积分的等效线性化方式是目前最常用的线性化处理方法。即对沿壁厚方向划分合理的单元个数，通过对评定路径的插值计算，将插值点各向应力分量按照合力等效原理进行均匀化处理，然后按照静力等效原理进行线性化处理，从而得到该路径下的薄膜应力分量、弯曲应力分量和峰值应力分量，最后计算相应的应力强度，并根据其结构和载荷特点进行应力分类。

ASME VIII-2(2007版)中指出，实体单元线性化处理过程中，除非是由扭转造成的线性分布的剪切应力，否则线性应力分布中一般不计入剪切应力。其中用于计算的应力分量是以应力分类线上的局部坐标为基础的，因此应力处理线上的薄膜应力张量是由应力分类线上各应力分量的平均值组成的，即：

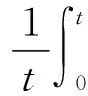
应力处理线上的弯曲应力张量则是由应力处理线上的各应力线性变化部分所组成的，即：

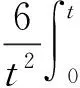
式中t——所考虑区域处的最小壁厚或容器厚度；

x——穿过壁厚的坐标。

由此可以计算应力处理线上的薄膜应力和薄膜加弯曲应力的应力强度或相当应力。

1.3 安全评定方法

ASME VIII-2(2007版)采用最大畸变能理论(MISES)来计算相当应力并用于进行强度评定；而JB 4732-1995(2005年确认)则采用最大剪切应力理论(TRSECA)来计算应力强度并进行强度评定，即：

Pm≤KSm

(1)

PL≤1.5KSm

(2)

PL+Pb≤1.5KSm

(3)

PL+Pb+Q≤3KSm

(4)

PL+Pb+Q+F≤Sa

(5)

式中F——峰值应力，由局部结构不连续或局部热应力引起的附加于一次加二次应力之上的应力增量；

K——载荷组合系数，由JB 4732-1995(2005年确认)中的表3-3查询得到；

Pb——一次弯曲应力；

PL——一次局部薄膜应力强度；

Pm——一次总体薄膜应力强度；

Q——二次应力，为满足外部约束条件或结构自身变形连续要求而所需的法向应力或剪应力；

Sa——根据设计疲劳曲线所得到的应力幅值；

Sm——设计温度下材料的许用应力。

应当指出，在应力分析中，一般难以将一次弯曲应力Pb分离出来，而是给出一次应力与二次应力之和，因此在安全评定时选用式(1)、(2)、(4)、(5)即可。

2 矩形压力蒸汽灭菌器的基本参数

矩形压力蒸汽灭菌器的结构示意图如图1所示。灭菌器的设计温度为127℃，工作温度129℃，设计压力0.17MPa，工作压力0.15MPa。筒体762mm×1062mm×6mm×1500mm，门框座1250mm×980mm×25mm，门板1118mm×848mm×10mm，门体侧齿和门框侧齿的齿宽为33mm，齿厚18mm，共15个，筒体加强筋90mm×40mm×8mm，门体加强筋130mm×65mm×10mm。筒体和门框座的材料为S30408，其他部件的材料为Q235B。

图1 矩形压力蒸汽灭菌器的结构示意图

3 有限元建模仿真与结果分析

3.1 实体单元有限元模型

由于灭菌器的结构和载荷分布具有对称性，因此选择结构的1/8建立有限元模型，则利用SOLID45单元建立的实体单元有限元模型如图2所示。两侧齿之间是接触关系，设置接触单元为CONTA174、目标单元为TARGE170，摩擦系数0.15，筒体内面施加内压0.17MPa，在门板表面上施加x、y方向的约束以限制模型沿x、y方向的平动，在对称面上施加对称约束，模型单元数为50 857个，节点数为44 380个。

图2 实体单元有限元模型

3.2 体-壳单元有限元模型

选用SHELL181单元对筒体和加强筋建立壳模型，选用SOLID45单元对结构不连续处即门框、门板和门齿建立实体模型，由于结构和载荷分布的对称性，选择结构的1/8建立有限元模型，具体如图3所示。两侧齿之间是接触关系，设置接触单元为CONTA174、目标单元为TARGE170，摩擦系数0.15。由于实体单元和壳单元的自由度个数不同，为保证求解精度故采用MPC方法[8,9]来实现实体单元与壳单元之间的连接，需要注意的是，设置实常数识别接触对。在筒体内面施加内压0.17MPa，在门板表面施加x、y方向的约束以限制模型沿x、y方向的平动，在对称面上施加对称约束，模型单元数为34 207个，节点数为17 708个。

图3 体-壳单元有限元模型

3.3 有限元计算结果

基于实体单元建模的矩形压力蒸汽灭菌器整体应力强度云图如图4所示，基于体-壳单元建模的矩形压力蒸汽灭菌器整体应力强度云图如图5所示。由图可知，实体单元模型和体-壳单元模型的TRSECA最大应力强度点均出现在远离端部的筒体倒圆角处，且前者的最大应力强度值为248.149MPa，后者最大应力强度为241.646MPa，两者的应力分布趋势几乎一致，相对误差为2.6%。

图4 实体单元整体应力强度云图

图5 体-壳单元整体应力强度云图

3.4 应力分类与结果分析

从图4、5的应力分布可以看出，门框、大门和远离结构不连续处的应力强度均小于材料的许用应力，可以不进行应力分析，而筒体的过渡圆角和筒体加强筋的过渡圆角处的应力较大，必须进行应力分析。

对采用实体单元建模的筒体圆角和加强筋圆角处做12条线性化处理路径，具体如图6所示。筒体处最大危险点出现在路径3-3处，加强筋最大危险点出现在路径9-9处。对采用壳单元建模的筒体圆角和加强筋圆角的相同位置提取节点应力，得到薄膜应力强度和薄膜加弯曲应力强度，结果见表1。

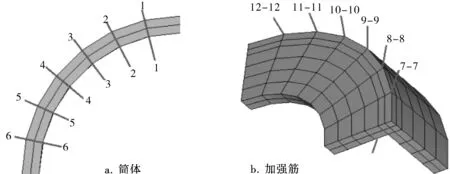
图6 应力线性化路径

MPa

由表1可知，壳单元与实体单元的应力计算结果相比，对于筒体倒圆角危险截面3-3处，无论是TRSECA应力强度还是MIESE等效应力，其局部薄膜应力值均偏小，而薄膜加弯曲应力偏大；对于加强筋危险截面9-9处，TRSECA应力强度的局部薄膜应力偏小而MIESE等效应力的局部薄膜应力偏大，二者的薄膜加弯曲应力均偏大，均满足强度要求。

对所有线性化处理路径得出的结果进行分析，得到不同位置的实体单元与壳单元模型的TRSECA应力强度结果如图7、8所示。

对于该矩形压力蒸汽灭菌器，危险点经过线性化处理之后，筒体倒圆角处的实体单元的薄膜应力均大于壳单元，相对误差为2.8%～9.5%，而薄膜加弯曲应力均小于壳单元，相对误差为2.1%～8.1%；对于加强筋倒圆角处，实体单元的薄膜应力大于壳单元，相对误差为0.23%～0.80%，薄膜加弯曲应力小于壳单元，相对误差为4.3%～4.9%。

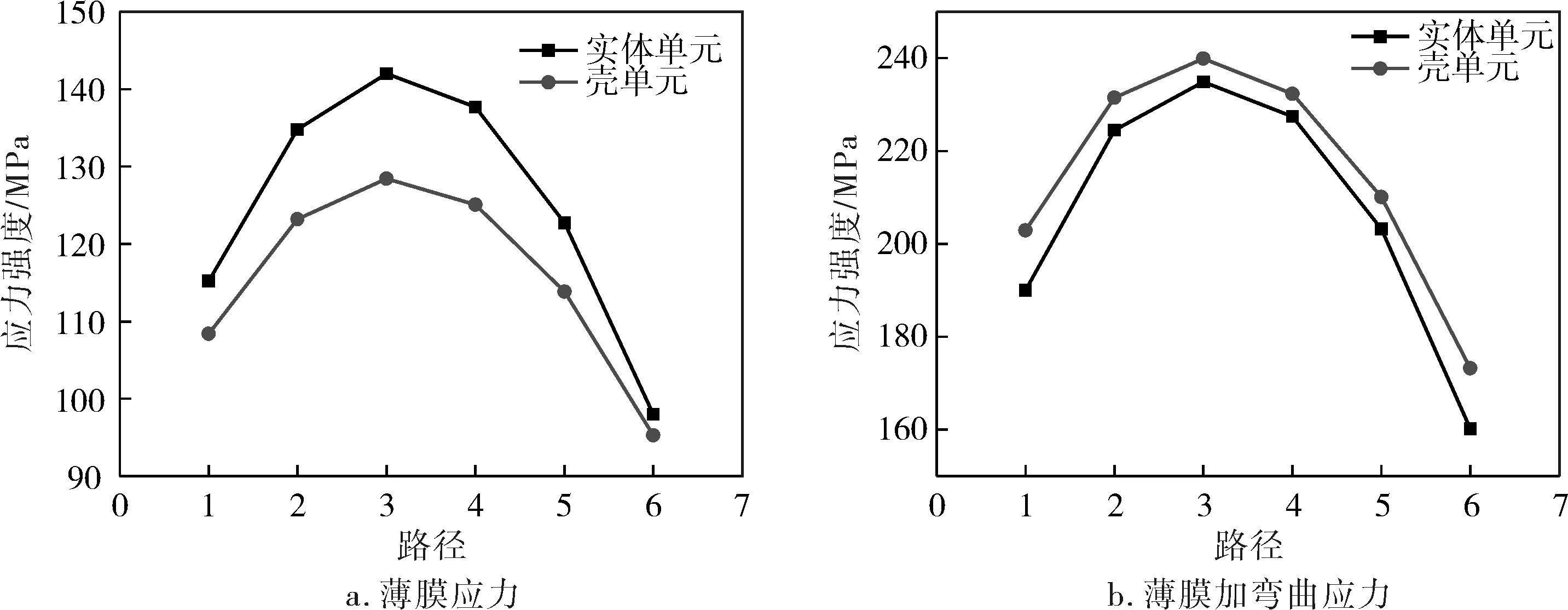
图7 筒体上不同路径下的应力强度

图8 加强筋上不同路径下的应力强度

4 结论

4.1与实体单元建模相比，体-壳单元建模简单、单元数少、占用内存少、计算速度快。

4.2实体单元与壳单元的应力分布基本一致，最大应力强度相对误差仅为2.6%，且危险点位于倒圆角处，符合其结构特征。

4.3壳单元与实体单元的计算结果相比，筒体的局部薄膜应力的应力强度值较小，加强筋的局部薄膜应力的应力强度值较大，而薄膜加弯曲应力的应力强度值均较大，其中局部薄膜应力的应力强度最大相对误差为9.5%，薄膜加弯曲应力的应力强度最大相对误差为8.1%，均在精度允许范围内，因此对该矩形容器采用壳单元分析是可行的。

4.4通过对矩形压力蒸汽灭菌器的有限元分析可知，对大型薄壁压力容器进行有限元分析时合理的采用壳单元代替实体单元进行计算，既可以得到较为精确的数值解，又可以降低资源的消耗，为类似工程的分析提供了依据。

[1] 沈瑾,张流波.压力蒸汽灭菌器的研究进展[J].中国消毒学杂志,2007,24(3):271～274.

[2] 杜伟,刘鹏飞,郑津洋,等.矩形蒸汽灭菌器强度数值模拟与试验研究[J].压力容器,2007,24(10):17～21.

[3] 曹占飞.用壳单元进行30°斜开孔补强计算的可行性研究[J].石油化工设备技术,2007,28(3):1～2.

[4] 陈小辉,董俊华,高炳军.壳单元在压力容器分析设计中的应用[J].河北工业大学学报,2010,39(5):29～32.

[5] 宋轶,腾儒民,陈礼.基于ANSYS壳单元与三维实体单元的锅炉管板分析[J].中国特种设备安全,2012,(7):8～10.

[6] 郭崇志,陈文昕,纪昌盛.大型薄壁压力容器Shell51单元模型的应力线性化分析[J].化工机械,2005,32(5):275～278.

[7] Jorge R M N,Fernandes A A.Design of a Steam-Heated Sterilizer Based on Finite Element Method Stress Analysis[J]. International Journal of Pressure Vessels & Piping,2001,78(9):627～635.

[8] 周艳,高耀东.利用MPC技术对SOLID 和SHELL单元进行连接[J].内蒙古科技大学学报,2011,30(3):241～243.

[9] 谢元丕,冯刚.ANSYS三维实体单元与板壳单元的组合建模研究[J].机械设计,2009,26(4):5～7.

ApplicationofShellElementandSolidElementinFiniteElementAnalysisofRectangularSteam-heatedSterilizer

LU Yan-ling, DONG Jin-shan, ZHU Xing-bang, YAO Yang, ZHAO Ning

(CollegeofMechanicalandPowerEngineering,NanjingUniversityofTechnology,Nanjing211816,China)

Both linearization method and safety assessment method for the shell element and solid element was described; and the structure parameter of rectangular steam-heated sterilizer was presented. Applying both solid element and solid-shell element methods to analyzing rectangular steam-heated sterilizer shows that, both elements can satisfy requirements of the structure strength. Comparing the shell element model with solid element model indicates that the maximal TRSECA stress intensity is resemble to the stress distribution and the intensity of local membrane stress is smaller and that of the membrane plus bending stress is bigger along with a 9.5% maximal relative error for the strength of local membrane stress and a 8.1% maximal relative error for the strength of membrane plus bending stress. These errors are within allowable accuracy range.

rectangular steam-heated sterilizer, finite element analysis, solid element, shell element

*卢艳玲，女，1989年5月生，硕士研究生。江苏省南京市，211816。

TQ051.3

A

0254-6094(2016)04-0495-05

2015-09-16，

2016-07-18)