关于套利组合最大收益问题的求解
毛克宁 林芳 王炜 魏嫚

摘要:本文从两个方面论述了套利组合最大收益问题的求解。一是对于一些简单情形直接用线性代数方法求解,分析和给出了这些情形下的某些结论。二是对于一般情形通过建立线性规划模型求解,并使得运算简化。
关键词:套利组合 最大收益 分析 求解
一、套利组合最大收益简单情形的求解
(一)概念与例的分析
分别用[xj]、[βji]和[E(rj)]表示按市值计算的投资者对证券[j]持有量的改变量、证券[j]的收益率对因素[i]的敏感度和证券[j]的期望收益率。套利组合满足以下三个条件:
[j=1nxj=0],(2)[j=1nβjixj=0 ( i=1, 2, …, s)],单因素模型为[j=1nβjxj=0],[j=1nxjE(rj)>0]。
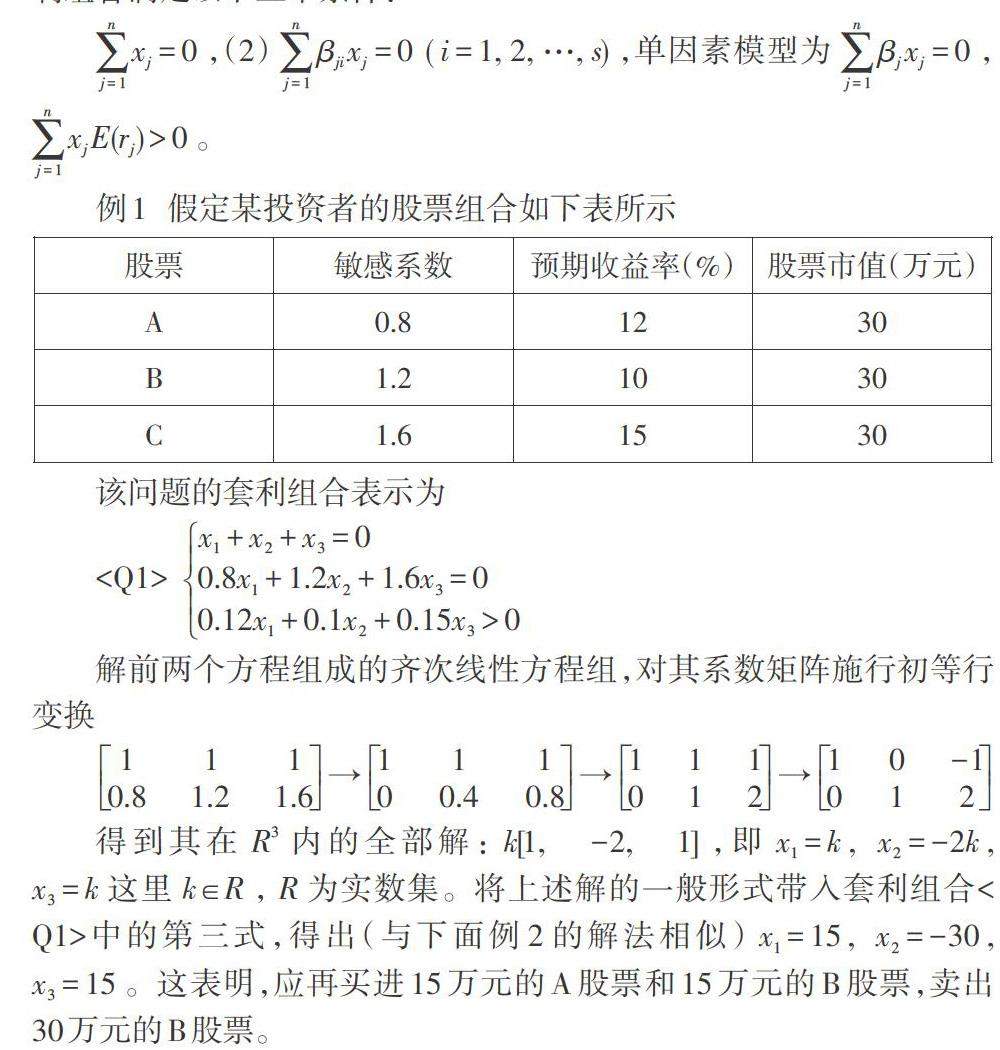
例1 假定某投资者的股票组合如下表所示
该问题的套利组合表示为
解前两个方程组成的齐次线性方程组,对其系数矩阵施行初等行变换
[1110.81.21.6→11100.40.8→111012→10-1012]
得到其在[R3]内的全部解:[k[1,-2,1]],即[x1=k], [x2=-2k], [x3=k]这里[k∈R],[R]为实数集。将上述解的一般形式带入套利组合
从该例看出,对于单因素套利模型,并非期望收益率最高的股票买进增量越大越好。在该例中,为获得套利组合的最大收益,并非将A股票和B股票全部卖掉后全部买进期望收益率最高的C股票。事实上,若将A股票和B股票全部卖掉而全部买进C股票,则有[x1=-30], [x2=-30], [x3=60]。这不满足
例2 假定某投资者的股票组合如下表所示
[股票\&敏感系数\&预期收益率
解前两个方程组成的齐次线性方程组(与例1完全相同),得到其在[R3]内的全部解:[k[1,-2,1]],即[x1=k], [x2=-2k], [x3=k] 这里[k∈R],[R]为实数集。将上述解的一般形式带入套利组合
该例中全部卖掉的不是期望收益率最低的C股票,而是期望收益率居中的B股票。事实上,若将C股票全部卖掉,即[x3=-30] 于是
以上两例对于为什么不一定要卖掉其他股票而全部购买期望收益率最高的股票或卖掉期望收益率最低的股票去买其他股票的分析,对于考虑交易费用的情形也是有意义的。
例1和例2都属于单因素套利模型的例子,对于一些简单的双因素套利模型仍可用类似的解法,这里不再赘述。注意到在例1的
(二)两只股票的单因素套利
假定某投资者拥有两只股票[A]与[B],[xA]与[xB]分别表示按市值计算的投资者对这两只股票持有量的改变量;[βA]与[βB]分别表示股票[A]与股票[B]的收益率对宏观因素的敏感度;[E(rA)]与[E(rB)]分别表示股票[A]与[B]的期望收益率。按照定义,套利组合必须满足以下部分条件:
这一齐次线性方程组
若[βA≠βB],则[D≠0],于是
分别以[pA(≥0)],[pB(≥0)]和[mA(≥0)],[mB(≥0)]表示股票[A]与[B]按市值计算的买进数量和卖出数量,于是[xA=pA-mA],[xB=pB-mB];分别以[aA(≥0)],[aB(≥0)]和[bA(≥0)],[bB(≥0)]表示买进和卖出股票[A]与[B]的交易费率,则这两只股票的单因素套利模型为
[xA+xB=0βAxA+βBxB=0E(rA)xA+E(rB)xB-(aApA+aBpB)-(bAmA+bBmB)>0]
若[βA=βB],则有
[xA+xB=0 ……①E(rA)xA+E(rB)xB>(aApA+aBpB)+(bAmA+bBmB) ……② ]
由①得[xB=-xA],将其代入②,有[(E(rA)-E(rB))xA>(aApA+aBpB)+(bAmA+bBmB) ]
若[E(rA)=E(rB)],则有[0>(aApA+aBpB)+(bAmA+bBmB)],但这显然是不可能的。因此,当[E(rA)=E(rB)]时,无套利机会。这在常识上不难理解:因为,若一个投资者仅持有两只股票,这两只股票的期望收益率相同并且对宏观因素的敏感度相同,则无需变动这两只股票的原持有量,即使变动也无法增加收益,而且在有交易费用的情况下,还会白白损失交易费用。这也说明了套利组合模型与“常识”是相吻合的。
由上面分析看出:若[E(rA)≠E(rB)]并且[βA=βB],则
当[xA]与[xB]正负相反,且[xA=xB>(aApA+aBpB)+(bAmA+bBmB)(E(rA)-E(rB)] 时,就实现了套利。
特别地,在不考虑交易费用的情况下,即当[aA=aB=bA=bB=0]时,不难看出:若[E(rA)>E(rB)]([βA=βB]),取[xA=yB],[xB=-yB](这里[yB]表示股票B按市值计算的原持有量),则可以获得最大套利收益;[E(rB)>E(rA)]的情况类似。
二、套利组合最大收益一般情形的求解
现在考虑一般情况下套利组合的最大收益问题。假设投资者原有的[n]只股票按市值计算的持有量分别为[y1(>0), y2(>0), …, yn(>0)],它们的改变量分别为[x1,x2,…,xn];这[n ]只股票改变后按市值计算的持有量分别为[z1,z2,…,zn],即[zj=xj+yj] ([j=1, 2,…, n])。以[pj]和[mj]分别表示股票[j]按市值计算的买进数量和卖出数量。这样,投资者按市值计算的对股票[j]持有量的改变量[xj]可表示为[xj=pj-mj]。分别以[aj(>0)]和[bj(>0)]表示买进和卖出股票[j]的交易费率([j=1, 2,…, n])。考虑交易费用的套利组合最大收益问题,可表示为线性规划模型LP:
[maxj=1n(pj-mj)E(rj)-j=1najpj-j=1nbjmj[6]]
[ j=1n(pj-mj)=0j=1nβji(pj-mj)=0 (i=1, 2,…, s)j=1n(pj-mj)E(rj)-j=1najpj-j=1nbjmj≥0 [7]mj≤yj pj≥0, mj≥0(j=1, 2, …,n)]
在参考文献[5]中,所举的例子属于单因素套利模型,为了使问题更具有一般性,下面考虑一个较为复杂的多因素套利模型的例子:
例3 假定某投资者拥有七只股票,情况如下表
[股票\&敏感系数βj1\&敏感系数βj2\&敏感系数βj3\&预期收益率(%)\&股票市值
这里引用一个参考文献[5]中的命题:将本文的线性规划模型LP中原标有上标的约束去掉后相应的线性规划模型记作LP。若LP有最优解,并且其目标函数最优值大于原标有上标的约束的不等式右端项,则LP的最优解也是LP的最优解,并且最优值不变。根据上述命题,LP的最优解存在且与LP的最优解相同,这可以通过LINDO软件的计算得以验证。
参考文献:
[1]赖家元,周文.证券投资学[M].华中科技大学出版社,2007
[2]北京大学数学力学系几何与代数小组,高等代数[M].高等教育出版社,1978
[3]薛嘉庆.线性规划[M].高等教育出版社,1989
[4]胡运权.运筹学教程[M].清华大学出版社,2012
[5]毛克宁.套利组合的最大收益模型研究[J].数学的实践与认识,2016,5,133-139
[6]谢金星,薛毅.优化建模与LINDO/LINGO软件[M].清华大学出版社,2005
[7]李晶莹,刘金兰.考虑交易成本的套利组合研究[J].中国管理科学,2002,10(专辑):229-232

