基于场协同理论的强化管换热效果分析*

张艾萍 夏荣涛 徐志明 丁 权 杨 钊 王 冲

(东北电力大学能源与动力工程学院)

基于场协同理论的强化管换热效果分析*

张艾萍*夏荣涛 徐志明 丁 权 杨 钊 王 冲

(东北电力大学能源与动力工程学院)

在湍流工况下，分别对圆管、横纹管、波节管和波纹管的换热效果进行数值模拟。应用场协同理论对数值模拟的结果进行分析，结果表明：各种换热管的努塞尔数和综合性能系数均随雷诺数的增加而增加，而场协同数则随雷诺数的增加而减小；当雷诺数较大时，各换热管的场协同数逐渐趋于定值；相同雷诺数下，横纹管的各项指标最高，而圆管最低。因此在相同工况下，应优先选择横纹管作为换热器中的强化换热管。

换热器 换热管 对流换热 场协同原理 场协同数 综合性能系数

随着现代工业的不断发展，换热器在热力发电、石油、化工、冶金及低温制冷等众多领域得到了广泛的应用。因此，增强换热器内流体扰动达到强化换热的目的，并同时减小其流动阻力，提高换热器的综合性能，是节约能源、减少能源浪费的有效途径，符合我国可持续发展的基本要求。

近几十年来，国内外学者在换热器的强化换热方面做出了重大贡献，但是他们对于对流换热的物理本质都没有做出详尽的解释。直到过增元院士提出了协同理论，从能量方程的角度出发，对对流换热的物理机理进行了阐述，得出了温度场与速度场的协同程度对对流换热有重大影响的结论[1]。在随后的十几年里，国内很多学者利用数值模拟和实验的方法对场协同理论进行了验证。在此基础上，刘伟等提出了多场协同理论，对强化换热的性能进行了评价并解释了流体减阻与换热强化的物理本质[2]；何雅玲等通过压力场、温度场和速度场三场协同性对高效低阻强化换热技术进行了探讨[3]；张毅等基于场协同理论对板式换热器的性能进行了数值优化[4]；张艾萍等应用三场协同原理，研究了污垢对圆管内层流换热的影响[5，6]。笔者通过场协同理论，分别对圆管、横纹管、波节管和波纹管进行数值模拟，对其换热效果进行了分析和比较。

1 三场协同强化传热理论

过增元和黄素逸从能量方程的角度出发提出了场协同理论，并指出对流换热不仅取决于流体的物性、速度和壁面与流体的温差，还取决于温度梯度与速度场的协同程度[7]；当流体具有相同的温度边界条件和相同的速度时，二者的协同程度越好其换热强度也越高。

三维场协同原理的关系式为[8]：

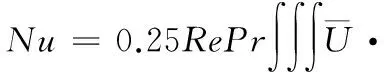
(1)

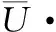
(2)

其中β为温度梯度矢量(热流矢量)与速度矢量之间的夹角。将式(2)代入式(1)，可得：

(3)

场协同数为：

(4)

当场协同数Fc=1时，则对流换热中热流场与速度场完全协同；当Fc<1时，热流场与速度场的协同程度有所减弱，换热效果较差。

2 模型的建立

2.1物理模型的建立

笔者对圆管、横纹管、波节管和波纹管三维物理模型进行数值模拟，各管的长度均为1 800mm，其中圆管内径D=25mm，并且忽略壁厚影响。为了使各管进出口能迅速达到湍流状态，在横纹管、波节管和波纹管的进出口都接有内径25mm、长80mm的直管段。各管的几何尺寸如图1所示，其中，横纹管的几何尺寸：φ1=25mm，φ2=21mm，L=30mm，R=0.5mm。波纹管的几何参数：D=25mm，d=21mm，s=30mm。波节管的几何参数：D1=25mm，D2=19mm，s1=8mm，s2=13mm，s=21mm。

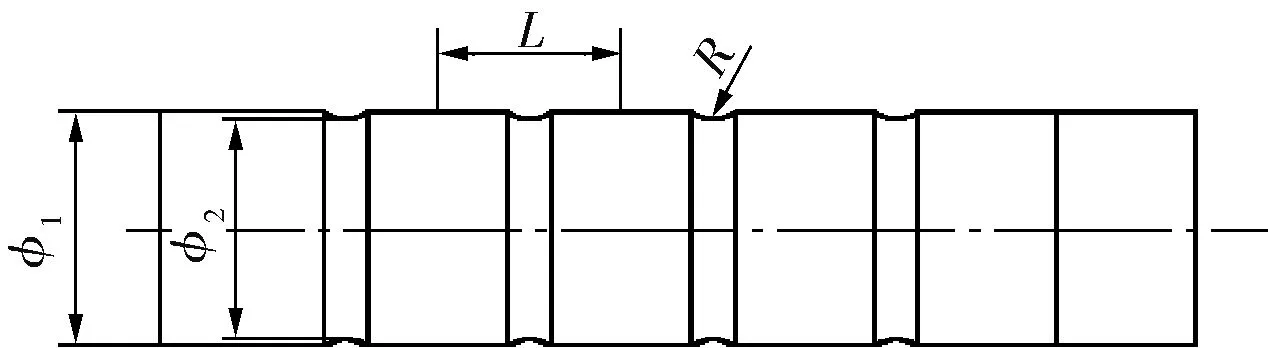
a. 横纹管

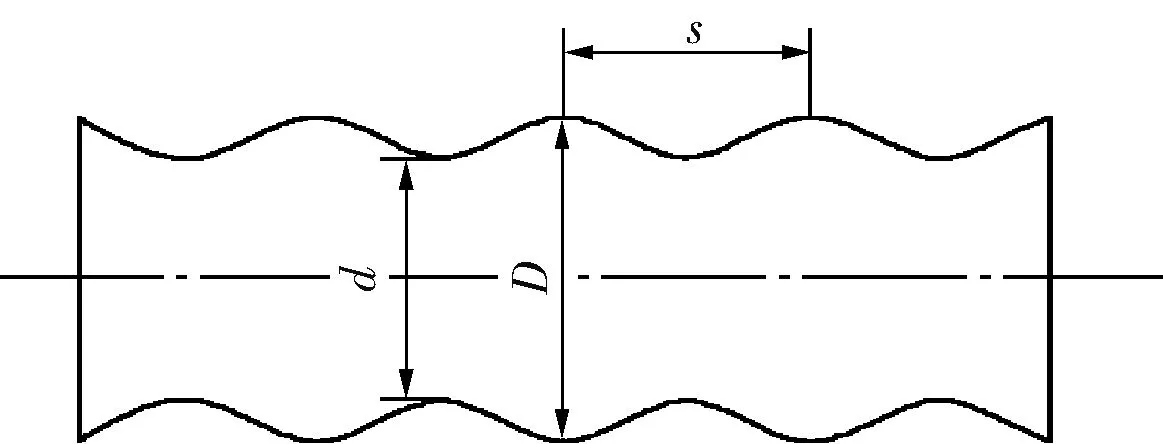
b. 波纹管

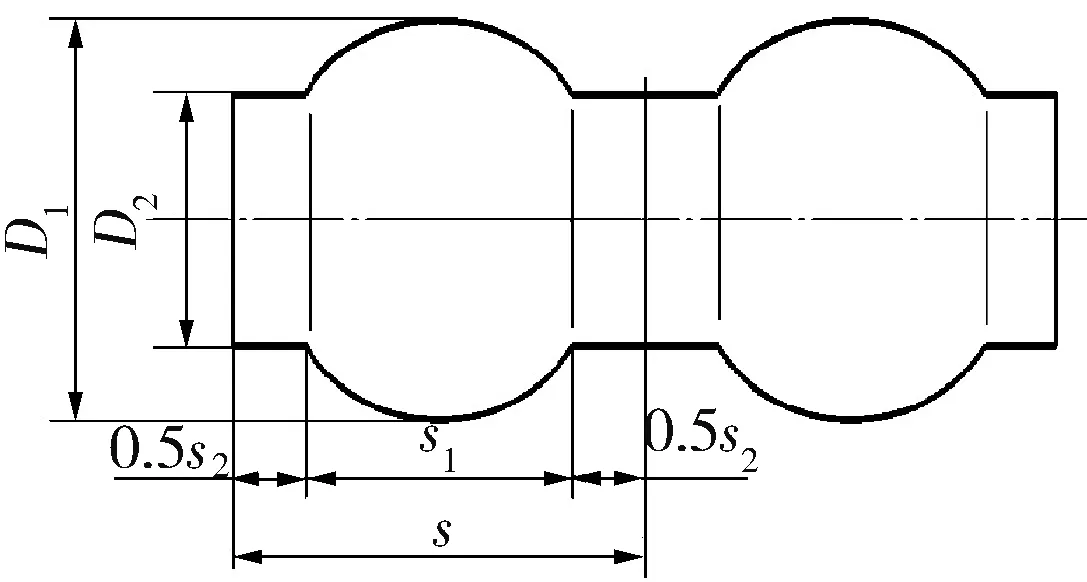
c. 波节管

2.2数学模型的建立

管内流体流动和热量传递均满足连续性方程、动量方程和能量方程。具体方程如下：

(5)

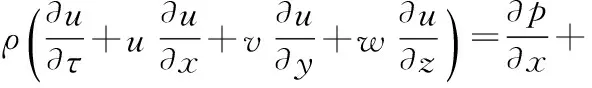
(6)

(7)

(8)

(9)

2.3初始条件和边界条件

笔者采用有限元差分法，二阶迎风差分格式，采用Standardk-ε模型，用SIMPLEC算法处理速度与压力耦合项。数值模拟中以水作为工质，并假设流体为不可压缩、常物性、稳态流动。操作压强为标准大气压，忽略重力的影响。能量方程、连续性方程和动量方程的计算迭代误差均为10-6。

边界条件的设置如下：各管的壁温均为350K，入口流体温度为300K。入口条件为velocity inlet，出口条件为outflow，内部为流体与固体耦合面，液固接触面间无滑移。

3 计算结果与分析

3.1努塞尔数的变化趋势

通过对圆管、横纹管、波纹管和波节管进行数值模拟，计算得出了努塞尔数Nu随雷诺数Re的变化关系(图2)。进口速度分别为0.8、1.0、1.2、1.5、1.8、2.0m/s。图2中的理论值是使用Gnielinski公式计算得出的圆管在6种不同工况下的努塞尔数，其计算结果与模拟值进行对比，相对误差都在10%以内，可知所选模型正确，边界条件合理。

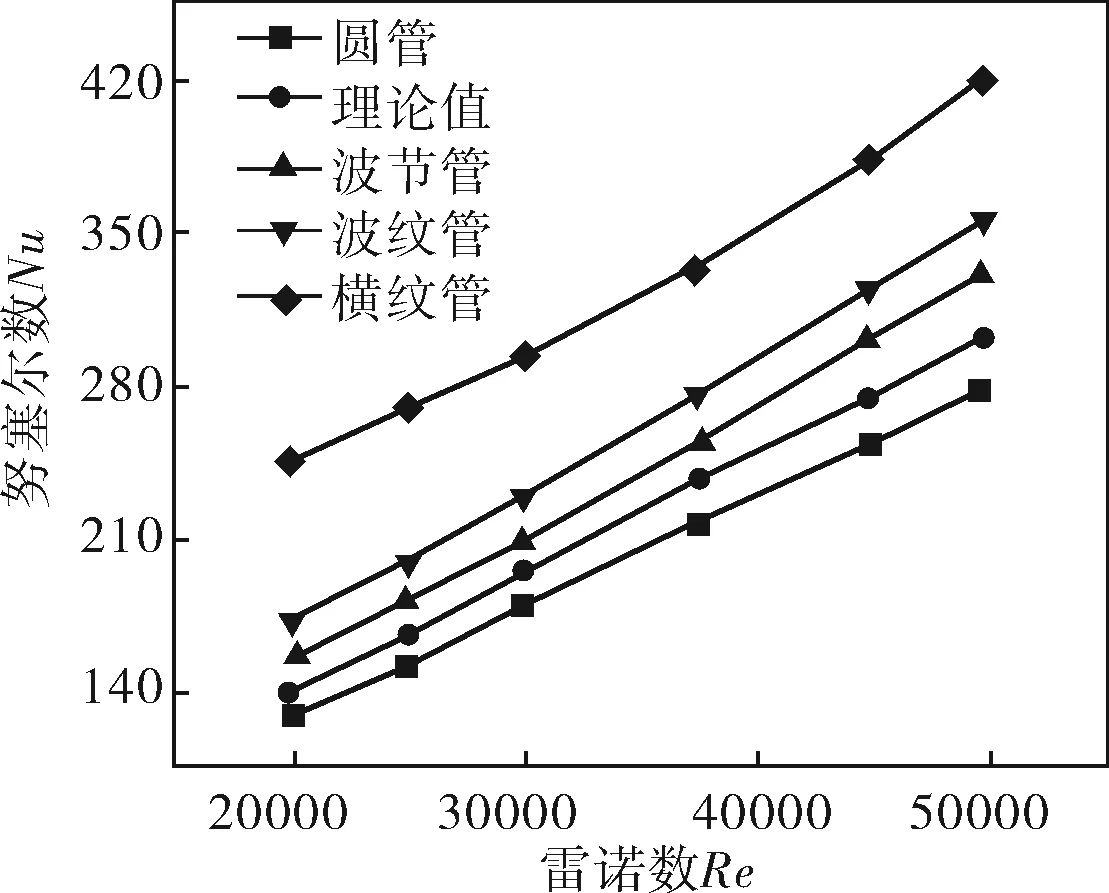
图2 努塞尔数Nu随雷诺数Re的变化

Gnielinski计算公式如下[9]：

(10)

其中，d为管径；l为管长；f为管内流体流动的Darcy阻力系数，按Filonenko公式计算f=(1.82lgRe-1.64)-2；ct=1.0077。

从图2中可以看出圆管、横纹管、波节管和波纹管的努塞尔数Nu均随着雷诺数Re的增大而增大。主要原因是随着雷诺数Re的增大，管内流体的湍流强度增加，减薄了壁面附近流体边界层的厚度，减小了换热阻力，增强了流体与壁面间的换热。由图还可以看出横纹管的换热能力最强，圆管最弱；经理论计算可知横纹管的换热能力大约是圆管的1.5～1.8倍。

图3为入口速度分别为1.0、2.0m/s时，圆管、横纹管、波节管和波纹管的速度等值线。从图3可以看出，当各管流体进口速度相同时，横纹管主流核心区速度最大，波纹管次之，而圆管最小。这是因为横纹管在横纹处面积突然缩小，管内压强增大，当流体离开横纹管最低处向直管过渡时，将流体的压力能转换为动能，增加了主流核心区的扰动，使换热能力增强；对于波节管，主要是流体进入波节处出现回流，增加了流体波节处的扰动，在壁面附近破坏了原有的边界层，使边界层减薄，从而使得换热能力也稍有增强；对于圆管，只有在主流核心区有扰动，但扰动较弱，导致壁面附近边界层较厚，增大了换热阻力，从而使得其换热效果较差。因此，从换热效果角度来看，横纹管的换热能力较强，使用横纹管来增强换热最为合理。

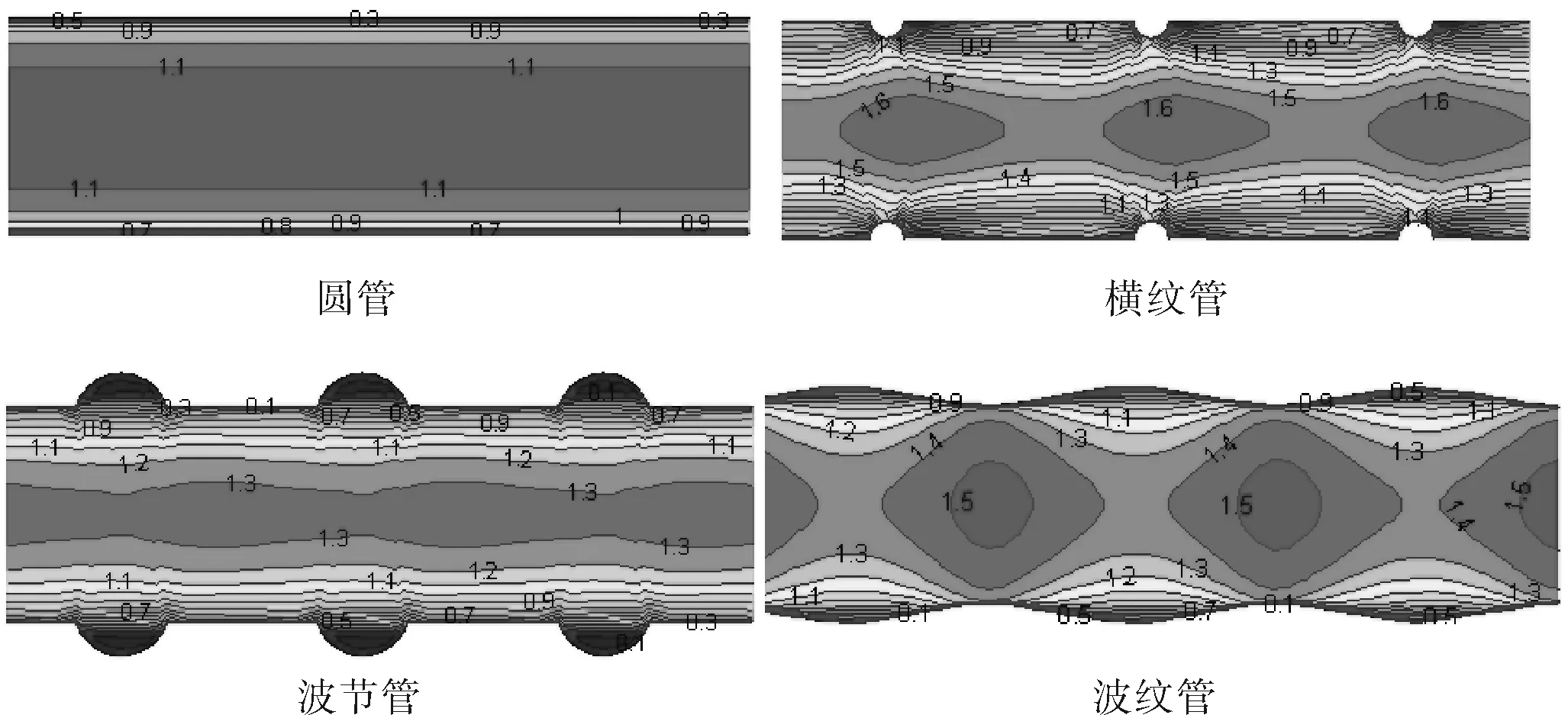
a. 入口速度1.0m/s

b. 入口速度2.0m/s

图3 不同工况下速度等值线

3.2场协同原理分析

为了更好地分析解释圆管、横纹管、波节管和波纹管的换热效果，分别对这几种不同的换热管应用场协同理论进行分析比较。

图4为圆管、横纹管、波节管和波纹管中场协同数Fc随雷诺数Re的变化情况。从图中可以看出：各换热管的场协同数Fc均随着雷诺数Re的增大而减小，当雷诺数Re很大时，各管的场协同数Fc变化趋势较平缓，逐渐趋近于固定值；横纹管的场协同数最大，波纹管次之，而圆管的场协同数最小；横纹管场协同数随雷诺数的增大变化较大，下降速率比其他各换热管的都大。

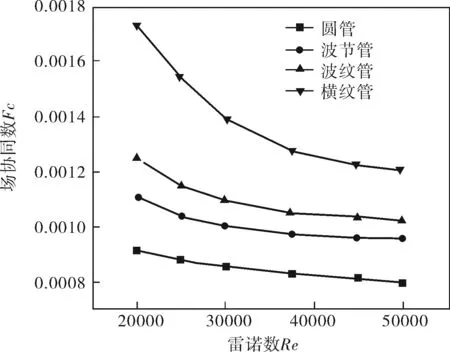
图4 场协同数Fc随雷诺数Re的变化

对于在紊流状态下，各种换热管的场协同数Fc均随着雷诺数Re的增大而减小，原因是当雷诺数Re增大时，努塞尔数Nu也随之增大，但是努塞尔数Nu增加的速率小于雷诺数Re增大的速率。当雷诺数增大很多时，二者的变化趋势几乎不变，然而研究流体的物理特性基本上没有改变。由公式Fc=Nu/(RePr)可知，当雷诺数Re增大时，场协同数Fc减小，最后趋于不变。

然而横纹管、波纹管、波节管的场协同数始终远大于圆管的，这是因为由于圆管管内流体湍流扰动较小，导致边界层相对较厚；在图3中可以看到圆管内流体的速度矢量方向基本是沿着管的轴向方向的。这两方面的原因使得圆管内温度梯度与速度矢量之间的夹角(场协同角β)接近90°，由式(3)可知圆管的努塞尔数较小，换热能力较差。而对于横纹管、波节管和波纹管来说，其结构是周期性变化的，也就使得管内流体存在相对较大的扰动，而且速度矢量的方向在轴向也发生周期性的变化，这种变化使得在管内的局部区域温度梯度与速度矢量的夹角小于90°，因此其换热能力远大于圆管的，换热效果较好。由公式Fc=Nu/(RePr)可知，当雷诺数一定时，圆管的场协同数较小，横纹管、波纹管、波节管的场协同数较大。

横纹管的场协同数下降速率比其他各管都快，主要是因为当流体速度增大时，即雷诺数增大，管内阻力也随之增大(远大于其他各管)，导致场协同数变化较快。因此，当雷诺数较小时，横纹管的换热能力更强。

3.3综合性能评价

流体在管道内流动过程中，在流体换热得到强化的同时，往往阻力损失也会增加。图5给出了进出口压差Δp随雷诺数的变化情况，从图中可以看出进出口压差Δp随雷诺数的增大而增大，横纹管的进出口压差Δp随雷诺数的变化较为剧烈，而圆管的变化则较为平稳。虽然横纹管的换热能力比其他管的换热能力强，但是阻力损失也较严重，这势必会增大消耗的泵功，在一定程度上造成能量的浪费。因此有必要用一个综合性能指标来评价各强化换热管的综合性能。

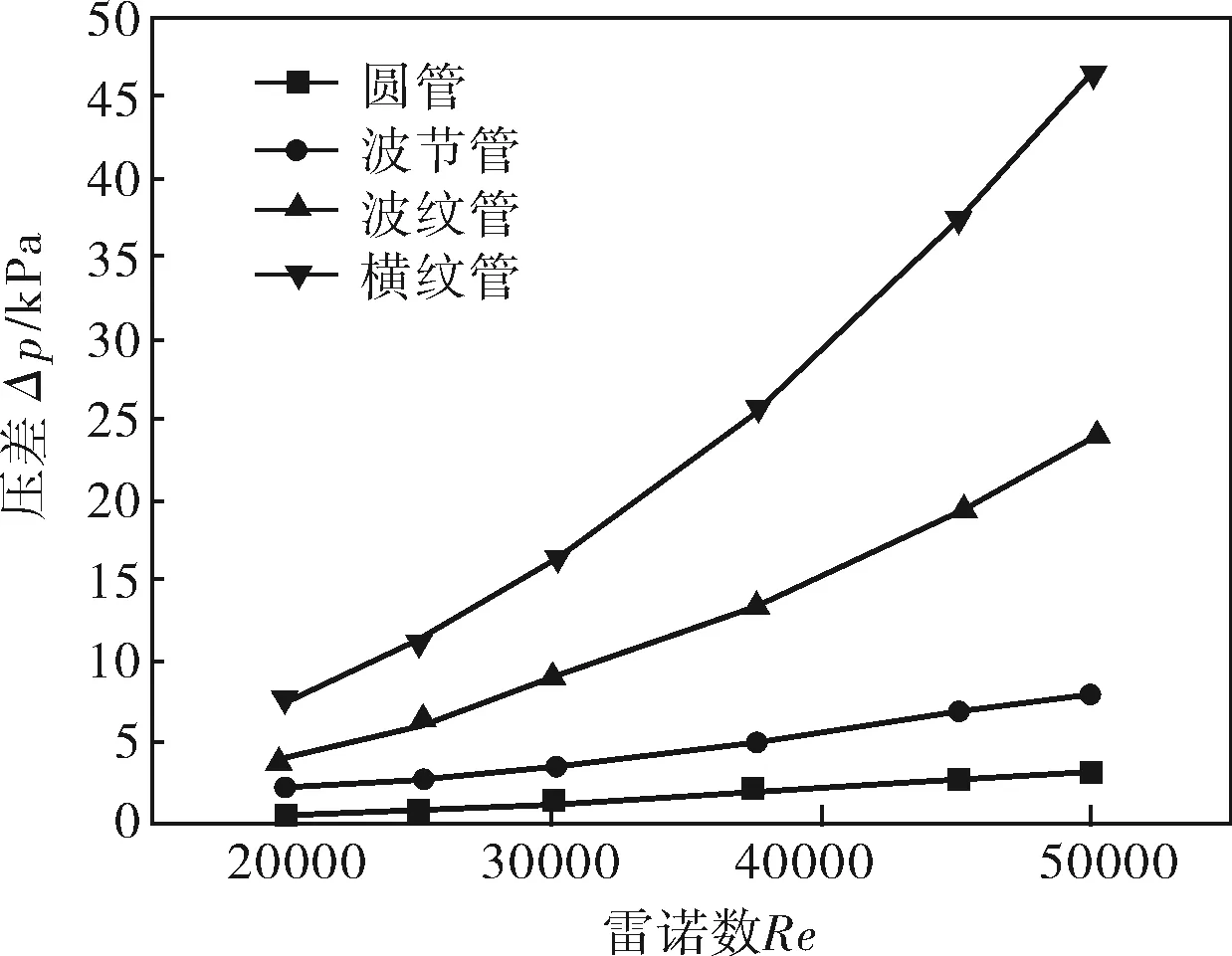
图5 压差Δp随雷诺数Re的变化

为了综合考虑强化换热能力和阻力损失，定义综合性能系数PEC为：

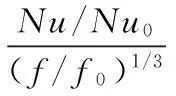
(11)

其中，Nu0和f0分别为圆管的努塞尔数和流体的阻力系数。

流体的阻力系数f计算公式为：

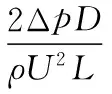
(12)

图6所示是以圆管为标准的综合性能系数PEC随雷诺数Re的变化关系。从图中可以看出随着雷诺数的不断增大，横纹管、波纹管、波节管的综合性能系数都增大，这表明提高流体的速度有利于强化换热。从图中还可以看出，无论是横纹管、波节管还是波纹管，其综合性能指标都大于1，这说明这几种强化换热管的综合性能均比圆管的好；而且在相同的雷诺数下，横纹管的最大，波节管次之，波纹管最小。

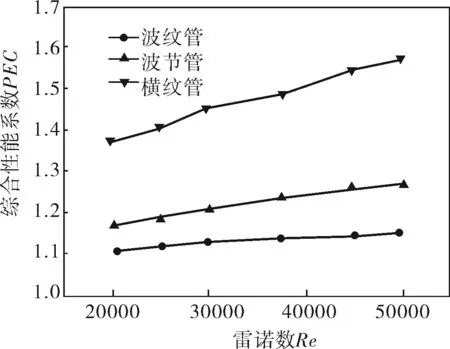
图6 综合性能系数随雷诺数的变化

4 结论

4.1笔者通过对圆管、横纹管、波节管和波纹管进行三维数值模拟得出，当流体处于湍流状态时，这几种换热管的努塞尔数Nu都随着雷诺数Re的增大而增大，并且在相同雷诺数下，横纹管的换热能力最强，波纹管次之，圆管最差。

4.2通过三维场协同理论分析得出，各种换热管的场协同数Fc也都随着雷诺数Re的增大而减小。当雷诺数较大时，各换热管的场协同数都趋于定值，这主要是因为努塞尔数增加的速率与雷诺数增加的速率大体相当。但是，当雷诺数较小时，横纹管的场协同数减小的速率较快，这是因为横纹管自身结构原因，当雷诺数增加时，管内阻力明显增加造成的。

4.3利用综合性能指标分析表明，横纹管、波纹管、波节管的综合性能都高于圆管，但横纹管的最好，因此当消耗泵功一定时，应优先选择横纹管。

[1] 过增元.换热器中的场协同原则及其应用[J].机械工程学报，2003，39(12)：1～9．

[2] 刘伟，刘志春，马雷.多场协同原理在管内对流强化传热性能评价中的应用[J].科学通报，2012，57(10)：867～874．

[3] 何雅玲，雷勇刚，田丽亭，等.高效低阻强化换热技术的三场协同性探讨[J].工程热物理学报，2009，30(11)：1904～1906．

[4] 张毅，董鹏飞，孙晓燕，等.基于场协同理论的板式换热器性能优化数值研究[J].化工机械，2013，40(4)：487～491.

[5] 张艾萍，徐志明，贺香英.污垢对管内层流对流换热场协同影响的数值研究[J].化工机械，2010，37(2)：204～207.

[6] 张艾萍，沈忠良，张宏学.污垢对圆管内层流换热三场协同的影响[J].东北电力大学学报，2014，34(5)：31～35．

[7] 过增元，黄素逸.场协同原理与强化传热新技术[M].北京：中国电力出版社，2004：10～11.

[8] 马小晶，胡申华，闫亚岭.波节管强化传热的三维数值模拟分析研究[J].水力发电，2012，38(1)：87～90.

[9] 杨世铭，陶文铨.传热学[M].北京：高等教育出版社，2006：248.

AnalysisofStrengtheningHeatTransferEffectsBasedonFieldSynergyTheory

ZHANG Ai-ping, XIA Rong-tao, XU Zhi-ming, DING Quan, YANG Zhao, WANG Chong

(CollegeofEnergyandPowerEngineering,NortheastDianliUniversity,Jilin132012,China)

In the turbulent flow conditions, the heat transfer effect of the circular tube, transversally-corrugated tube and the corrugated pipe was simulated respectively. Applying the field synergy theory to analyze these simulation results shows that Nusselt number and overall coefficient of performance of various tubes can be increased with the increase of Reynolds number while the field synergy number decreases with increasing of Reynolds number; when the Reynolds number becomes larger, the field synergy number of various tubes tends to a definite value; regarding the same Reynolds number, the indicators of transversally-corrugated tube are the highest and those of the circular tube are the lowest; as for the same conditions, the preference should be given to the transversally-corrugated tube.

heat exchanger, heat exchange tube, convective heat exchange, field synergy theory, field Synergy number, overall coefficient of performance

TQ051.5

A

0254-6094(2016)01-0097-05

*国家自然科学基金资助项目(51476025)。

**张艾萍，男，1968年2月生，教授。吉林省吉林市，132012。

2015-02-03)