基于二次型约束的稳健宽带恒定束宽波束形成*

陈 辉 赵拥军 刘成城 丁永超

(解放军信息工程大学导航与空天目标工程学院，郑州,450001)



基于二次型约束的稳健宽带恒定束宽波束形成*

陈 辉 赵拥军 刘成城 丁永超

(解放军信息工程大学导航与空天目标工程学院，郑州,450001)

针对期望信号导向矢量失配时传统宽带波束形成器性能恶化的问题，提出一种稳健的宽带恒定束宽波束形成算法。首先结合空间响应变化(Spatial response variation, SRV)约束，将算法在信号带宽内不同频点的阵列响应约束简化为对某一参考频点的约束，实现具有恒定束宽特性的宽带波束形成，再通过对权矢量模值施加二次不等式约束，抑制指向误差及传感器参数随机扰动误差，提高算法的稳健性，并通过拉格朗日乘子法，在约束边界上求得最优权矢量的解析解。实验结果表明算法可有效克服信号指向误差引起的波束形成器性能恶化问题，且具有良好的恒定束宽特性及较高的阵列输出性能。

宽带波束形成；稳健性；恒定束宽；空间响应变化约束；二次型约束

引 言

自适应波束形成技术广泛应用于雷达、无线通信、声纳和麦克风阵列等领域，是阵列信号处理的研究热点之一[1-3]。波束形成的主要目的是对不同来向的阵列接收信号进行采样，并通过一定的加权处理，增强期望信号，同时抑制干扰信号和噪声。为了获得较高的阵列输出性能，许多经典的波束形成算法相继提出。文献[4,5]提出的线性约束最小方差(Linearly constrained minimum variance, LCMV)算法可自适应地抑制干扰信号，然而实际应用中，由于幅度误差、阵元位置误差和角度失配等原因，常会造成波束形成器性能下降，严重时甚至会出现信号对消。

为了提高算法的稳健性，文献[6]给出了一种调整期望信号导向矢量的方法，但该算法需要已知参考信号。文献[7]对期望信号指向施加导数约束，当存在指向误差或幅相误差时具有较好的稳健性，但该算法需对接收信号进行预延迟补偿，不利于数字实现。文献[8]利用混合最速下降法实现了存在指向误差时的稳健宽带波束形成，但该算法模型复杂，硬件实现困难。文献[9]结合最差性能最优准则，在信号频段范围内选取离散频率点，对其施加阵列响应约束，可有效抑制期望信号指向误差。然而，该方法无法控制阵列响应的频率一致性，且误差存在时对不同采样频点均施加约束会过多地消耗阵列自由度，算法抑制干扰能力降低。文献[10,11]将不同频点的阵列响应约束简化为对某一参考频点的约束，并结合凸优化理论，解决了波束形成器对期望信号指向误差敏感的问题，但这两种算法均采用迭代求解，无法给出最优权矢量的解析解。

本文从宽带时域模型出发，结合空间响应变化(Spatial response variation, SRV)约束，得到具有恒定束宽特性的宽带波束形成算法，再对权矢量模值施加二次型不等式约束，抑制指向误差及传感器参数随机扰动误差引起波束形成器性能的恶化，并通过拉格朗日乘子法求解得到约束条件下的最优权矢量，最后给出仿真实验与对比分析。

1 信号模型

时域宽带波束形成器一般结构如图1所示。假设远场宽带信号以方位角θ(定义为信号入射方向与线阵法线的夹角)入射到M阵元均匀直线阵，每个阵元后所接抽头延迟线长度为J，则波束形成器的阵列响应可表示为

(1)

式中：(·)*表示共轭操作;Δτ=(d/c)sinθ，其中d和c分别代表阵元间距和波的传播速度;Ts为采样间隔。为了防止空间混叠，常取d为信号最高频率对应波长的一半，w为权系数向量，s(θ,f)为对应的导向矢量。

图1 TDL宽带波束形成器结构Fig.1 Wideband beamforming structure based on tapped delay-lines

假设期望信号沿垂直方向(θ=0)入射，LCMV波束形成器可以表示为

(2)

式中:Rx=E[x(t)xH(t)]为阵列接收数据协方差矩阵;f为J×1维阵列响应向量，满足某一元素为1，其他元素为0;C为MJ×J维约束矩阵，即

(3)

式中：1M和0M分别为M×1维全1和全0列矢量。当期望信号沿非零度入射时，需对各通道接收数据进行预延迟补偿，使期望信号等同于垂直入射[12]。

式(2)可以通过拉格朗日方程求解，其解为

(4)

Rx通过有限次快拍估计得到

(5)

其中K为采样快拍数。

2 波束形成算法

本文首先结合SRV约束，给出一种具有恒定束宽特性的宽带波束形成算法，再通过对权矢量施加二次不等式约束，实现算法的稳健性，并利用拉格朗日乘子法，在约束边界上求得算法最优权矢量。

2.1 恒定束宽波束形成器

假设宽带信号频率范围为[fl,fh]，期望信号入射角为θ0。定义接收信号频带范围内方位角θ处空间响应变化程度[13]为

(6)

其中f0为参考频点，带宽B=fh-fl，D(θ)为MJ×MJ维矩阵，即

(7)

参量SRV表示波束形成器在某一方位角θ处的空间响应变化程度，即θ方向上不同频点f∈[fl,fh]处阵列响应相对于f0处阵列响应的均方误差。扩展到整个角度覆盖范围，并对参量SRV求均值，可得

(8)

式中ΘFI表示信号覆盖角度范围，通过等间隔选取角度信息，将式(8)写成离散形式，有

(9)

(10)

权重因子ρ满足0≤ρ≤1。结合式(2)可得具有恒定束宽特性的宽带自适应波束形成算法

(11)

具有恒定束宽特性的波束形成算法可仅对参考频点约束，其他频点的阵列响应通过SRV约束拟合到参考频点，算法无需预延迟补偿，可实现对任意来向宽带信号的有效接收。设期望信号沿θ′方向入射，此时

(12)

其中

(13)

对式(11)求解可得该约束条件下的最优权系数。

2.2 基于二次型约束的稳健算法

(14)

结合式(11)，二次型约束稳健宽带恒定束宽波束形成算法可以表示为

(15)

用T表示上式描述的约束条件集合，有

(16)

对算法进行求解，定义函数

(17)

其中λ为实值拉格朗日常数，同时满足Rx+λI>0,λ≥0，μ为拉格朗日乘数矢量，有

(18)

等号在T的边界上取得。不考虑二次不等式约束时，波束形成器最优权矢量为

(19)

若

(20)

则w1即为满足约束条件下的最优解，此时ε取值选取过大，算法稳健性较差。为了得到较好的稳健性，需满足

(21)

式(17)对复向量w求导,并令其为零,有

(22)

(23)

(24)

有

(25)

解得

(26)

(27)

上式对μ求导并令其为零，得

(28)

(29)

求f2(λ)关于λ的最大化，可得

(30)

λ可通过牛顿迭代法求解。此时

(31)

3 仿真实验

3.1 性能分析

考虑一阵元数为15的均匀直线阵，抽头延迟线长度J=15，期望信号来向θ0=20°，信号最低频率fl=400 MHz，最高频率fh=600 MHz，两宽带干扰信号分别沿-20°和50°方向入射，最低频率均为400 MHz，最高频率均为600 MHz，中心频率为500 MHz，信噪比为10 dB，信干比均为-40 dB。以中心阵元为参考阵元，阵元间距为期望信号最高频率对应波长的一半，快拍数为512。

图2和图3分别给出了ρ=0.001时,本文算法的二维阵列响应和幅度响应。由阵列响应图可以看出，算法阵列响应主波束指向正确，在干扰信号来向-20°和50°方向上形成了较深的零陷，且具有较好的恒定束宽特性。由幅度响应结果可以看出，算法在期望方向具有较好的频率一致性，各频点在该方向上阵列响应增益均逼近0 dB，算法可自适应地抑制强干扰信号，在干扰信号来向上抑制能力达40 dB以上。本文算法无需预延迟补偿，可直接对期望信号沿非0°方向入射的接收信号实现空域滤波，避免了由于预延迟补偿误差引起的波束形成器性能下降的问题。

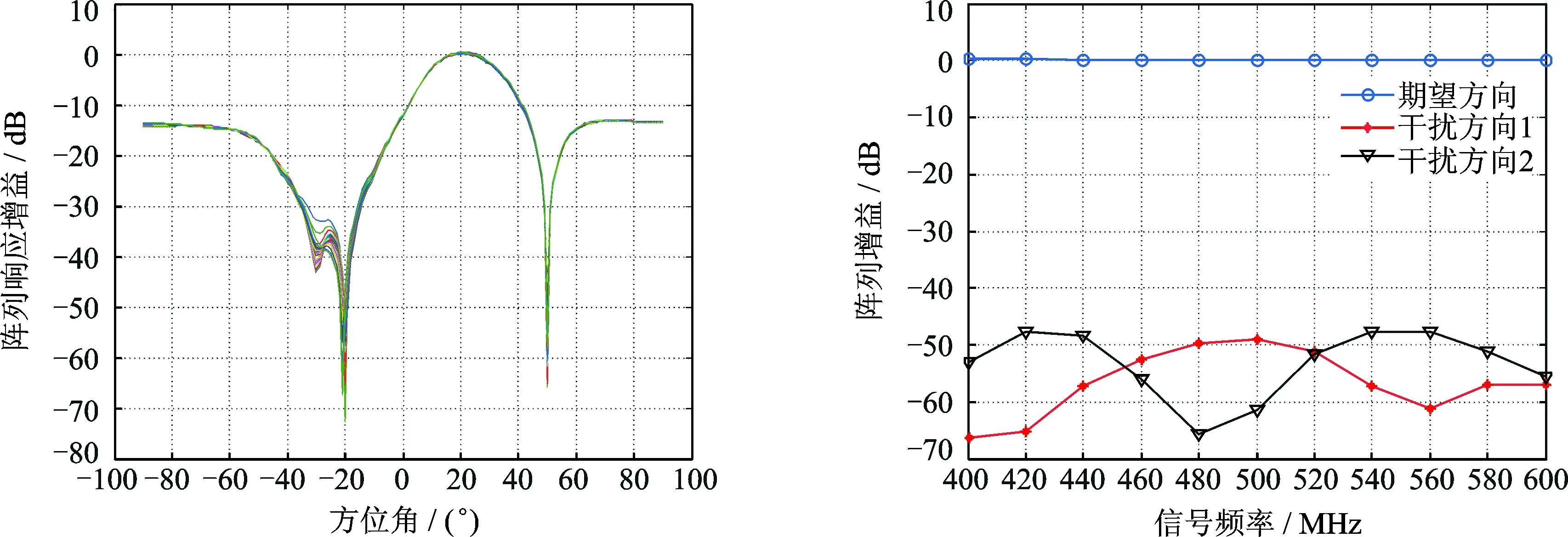
图2 本文算法二维阵列响应图Fig.2 2-D beam response of the proposed algorithm图3 本文算法阵列幅度响应Fig.3 Magnitude response of the proposed algorithm

其他条件不变，图4(a，b)分别给出了估计期望信号来向存在3°误差时恒定束宽(未做稳健处理)算法与稳健算法的二维阵列响应图。由以上结果可以看出未做稳健处理时期望信号被当作干扰对消，波束形成算法失效，而本文稳健算法主波束指向正确，在干扰方向产生较深的零陷，且保持较好的频率一致性。

图4 存在误差时算法二维阵列响应图Fig.4 2-D beam response when there exist look direction estimation errors

图5 输出SINR随输入信噪比变化曲线Fig.5 Output SINR versus input SNR图6 输出SINR随期望信号角度估计误差变化曲线Fig.6 Output SINR versus angle estimation errors

3.2 参量取值

图7 本文算法输出信干噪比随权重因子ρ变化曲线Fig.7 Output SINR versus weight factor ρ

图7给出了参量ρ改变时本文恒定束宽算法和存在3°指向误差时稳健算法输出信干噪比性能变化曲线。由该图可知，恒定束宽算法与稳健算法均在ρ=0.001附近取得最优值，且存在指向误差时稳健算法输出信干噪比性能仅略低于信号来向估计准确时算法的输出性能。本文算法对输出方差和频率一致性两个指标同时优化，ρ的取值大小决定着这两个指标在优化过程中所占的比重。本文算法仅对参考频点施加线性约束，其他频点通过频率不变性向参考频点拟合，只有在首先保证算法频率一致性良好时才能得到有效的波束输出，要得到较高的阵列输出性能，算法对频率一致性的约束比重需大于对输出方差的约束。

3.3 计算复杂度分析

以阵元个数M=15，抽头延迟线长度J=15为例。文献[10]和文献[11]利用凸优化求解，其计算量与迭代次数、优化变量个数和二阶锥维数有关。

表1给出了文献[10]和文献[11]两种算法的计算复杂度。本文算法给出了权矢量的解析解，其中矩阵求逆运算计算量量级为O(K3)，K为矩阵维数，本文算法求逆过程计算量为O(M3J3)+O(J3)，乘法计算量为M2J3+MJ3+M2J3+MJ3+MJ2=2M2J3+2MJ3+MJ2。与表1两种算法对比，本文算法计算量远小于其他两种算法，具有较低的计算复杂度。

表1 算法计算复杂度

4 结束语

本文针对实际应用中存在指向误差及传感器参数随机扰动误差时宽带波束形成器性能下降的问题，提出一种基于二次不等式约束的稳健自适应波束形成方法。首先结合SRV约束，实现具有恒定束宽特性的宽带波束形成，再对权矢量模值施加二次不等式约束，提高算法的稳健性，并给出算法解析解。算法在存在期望信号估计误差时，仍可较好地实现对期望信号的有效接收，具有较高的阵列输出性能和良好的恒定束宽特性。同时，算法不受时域模型的限制，可扩展至阵元延迟线模型。

[1] Zhao Y, Liu W. Robust wideband beamforming with frequency response variation constraint subject to arbitrary norm-bounded error[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(5): 2566-2571.

[2] 李静, 陈华伟. 基于正则化约束最小二乘的稳健频率不变波束形成器设计方法[J]. 数据采集与处理, 2012, 27(2): 202-209.

Li Jing, Chen Huawei. Robust FIB design using regularized constrained least squares[J]. Journal of Data Acquisition & Processing, 2012,27(2): 202-209.

[3] Michail M, Paul D K, George K, et al. Mutual information statistics and beamforming performance analysis of optimized Los MIMO systems[J]. IEEE Transactions on Communications, 2010, 58(11): 3316-3330.

[4] Frost O L, III. An algorithm for linearly constraints adaptive array processing[J]. Proceedings of the IEEE, 1972, 60(8): 926-935.

[5] 王立兵, 韩宁, 龚文飞. 可用于快速搜索卫星信号的降维空时波束形成算法[J]. 南京航空航天大学学报, 2013, 45(3): 402-409.

Wang Libing, Han Ning, Gong Weifei. Improved reduced-rank space-time adaptive beamforming algorithm for fast search of satellite signal[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(3): 402-409.

[6] Hoshuyama O, Sugiyama A, Hirano A. A robust adaptive beamformer for microphone arrays with a blocking matrix using constrained adaptive filters[J]. IEEE Transactions on Signal Processing, 1999, 47(10): 2677-2684.

[7] Zhang S T, Thng I. Robust presteering derivative constraints for broadband antenna arrays [J]. IEEE Transactions on Signal Processing, 2002, 50(1): 1-10.

[8] Slavakis K, Yamada I. Robust wideband beamforming by hybrid steepest decent method [J]. IEEE Transactions on Signal Processing, 2007,55(9): 4511-4522.

[9] Rubsamen M,Gershman A B.Robust presteered broadband beamforming based on worst-case performance optimization[C]∥2008 5th IEEE Sensor Array and Multichannel Signal Processing Workshop. Darmstadt:[s.n.], 2008: 340-344.

[10]Zhao Y, Liu W, Richard J L. Adaptive wideband beamforming with response variation constraints[C]∥European Signal Processing Conference. Aalborg, Denmark:[s.n.], 2010: 23-27.

[11]Wang W Q, Liu C C, Zhao Y J, et al. A novel probability- constrained approach to robust wideband beamforming with sensor delay lines[C]∥IET International Radar Conference 2013. Xi′an:[s.n.], 2013: 1-5.

[12]鄢社锋, 马晓川. 宽带波束形成器的设计与实现[J]. 声学学报, 2008, 33(4): 316-326.

Yan Shefeng, Ma Xiaochuan. Designs and implementations of broadband beamformers[J]. Chinese Journal of Acoustics, 2008, 33(4): 316-326.

[13]Duan H P, Boon P N, Chong M S, et al. Applications of the SRV constraint in broadband pattern synthesis[J]. Signal Processing,2008,88(4):1035-1045.

陈辉(1989-)，男，硕士研究生，研究方向：阵列信号处理，E-mail: chhui891206@163.com。

丁永超(1989-)，男，硕士研究生，研究方向：阵列信号处理。

赵拥军(1963-)，男，博士，教授，博士生导师，研究方向：阵列信号处理、雷达信号与信息处理。

刘成城(1986-)，男，博士研究生，研究方向：阵列信号处理、目标探测与识别。

Robust Wideband Constant Beamwidth Beamforming Algorithm Based on Quadratic Constraint

Chen Hui， Zhao Yongjun， Liu Chengcheng， Ding Yongchao

(Navigation and Aerospace Target Engineering Institute, PLA Information Engineering University, Zhengzhou, 450001, China)

A robust wideband constant beamwidth beamforming algorithm is proposed to solve the problem of performance degrade of traditional wideband beamforminers when there exists steering vector error. With the spatial response variation (SRV) constrain, a wideband constant beamwidth beamforming algorithm can be obtained by simplifying the response at different frequencies as a reference frequency. Then the robustness of beamformer can be improved by imposing the quadratic constraint for the weight vector. Finally, the optimal weight with a closed form can be solved on the boundary of uncertainty set using the Lagrangian method. Experiments illustrate that the algorithm obtains a desired result to against the look direction estimation error, and achieves a preferable constant beamwidth performance and a high output signal to interference plus noise ratio.

wideband beamforming; robustness; constant beamwidth; spatial response variation(SRV) constrain; quadratic constraint

国家高技术研究发展计划(“八六三”计划)(2011AA7031015)资助项目。

2014-11-13；

2015-10-12

TN911.7

A