未知互耦下双基地MIMO雷达阵列DOD和DOA估计算法*

戴继生 汪 洋 叶中付

(1.江苏大学电气信息工程学院，镇江，212013； 2.中国科学技术大学电子工程与信息科学系，合肥，230027)



未知互耦下双基地MIMO雷达阵列DOD和DOA估计算法*

戴继生1汪 洋1叶中付2

(1.江苏大学电气信息工程学院，镇江，212013； 2.中国科学技术大学电子工程与信息科学系，合肥，230027)

针对MIMO雷达阵列中存在的互耦效应会严重影响发射角(DOD)和接收角(DOA)估计性能的问题，提出了一种基于ESPRIT算法的双基地MIMO雷达阵列DOA和DOD估计方法。该方法利用阵列流型矩阵的结构特点和均匀线阵互耦矩阵的带状Toeplitz特性，能实现互耦效应未知情况下DOA和DOD的精确估计。本文方法无需对角度进行搜索，计算量小，对角度的估计精度高，特别是在低信噪比环境下依然能取得较好的估计性能。仿真结果验证了本算法的可行性和正确性。

阵列信号处理；MIMO雷达；互耦；接收角估计；发射角估计

引 言

近几十年来，目标角度估计一直是雷达信号处理领域的一个重要研究内容，利用双基地多输入多输出(Multi-input multi-output，MIMO)雷达系统进行发射角(Direction of departure，DOD)和接收角(Direction of arrival，DOA)估计时，其分辨率明显优于传统的相控阵雷达[1-4]。针对双基地MIMO 雷达信号的DOD 和DOA 估计问题，人们提出了许多行之有效的方法，取得了一些重要进展[5-11]。但现有方法对双基地MIMO雷达阵列阵元之间的互耦效应考虑较少。阵元间耦合的现象普遍存在于阵列天线系统中，互耦效应的存在会导致各类算法的角度估计性能急剧下降。为解决该问题，Liu等人提出了一种未知互耦条件下的双基地MIMO雷达DOD和DOA估计方法[12]。该方法能够消除互耦效应带来的不利影响，提高目标角度的估计性能。但该方法不仅需要进行多次谱峰搜索，还需对角度行配对，这使得算法的计算复杂度较高。本文针对MIMO雷达系统中存在的互耦效应会严重影响DOD和DOA估计性能这一问题，提出了一种基于旋转不变子空间(Estimation of signal parameters via rotational invariance techniques, ESPRIT)算法的双基地MIMO雷达阵列DOD和DOA估计方法。该方法利用阵列流型矩阵的结构特点和均匀线阵(Uniform linear array, ULA)互耦矩阵的带状Toeplitz特性，能实现在互耦效应未知情况下DOD和DOA的精确估计和配对。此外，本文方法无需对角度进行搜索，计算量小，对角度的估计精度高，特别是在低信噪比环境下依然能取得较好的估计性能。

1 信号模型

考虑一个由M个发射阵元和N个接收阵元组成的双基地MIMO雷达系统，其发射阵列和接收阵列均为均匀线阵。发射和接收阵列的阵元间距均为λ/2(λ为载波波长)。设Ct和Cr分别表示发射阵列和接收阵列的互耦矩阵，由于互耦系数与阵元间距呈反比，足够远的两阵元间互耦系数近似为0，且间距相同的阵元间互耦系数相同[13,14]。因此，不失一般性，假设发射和接收阵列的互耦矩阵中非零互耦系数的个数为K，即

(1)

式中ctk和crk(k=1,2,…,K)为互耦系数。若远场信号源个数为P，其中第p个信号的DOD和DOA分别记为θp和φp，则接收信号可表示为

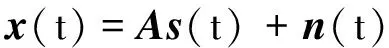
(2)

Es=AT

(3)

2 未知互耦条件下目标角估计算法

对于无互耦(K=0)条件下双基地MIMO雷达的DOA和DOD估计算法，本文不再赘述，详见参考文献[15]。本节将提出一种未知互耦(K>0)条件下，基于ESPRIT算法的DOA和DOD估计算法。

2.1 DOA估计

当存在互耦效应时，文献[15]所述方法不再适用。为解决该问题，可以利用带状对称Toeplitz的结构特点以及Kronecker积的性质，定义一个常量矩阵Fr]并将其左乘ap，可得

(4)

(5)

由式(5)可见，虽然arp未包含导向矢量的全部信息量，但它能消除互耦效应带来的影响，恢复阵列流型矩阵的旋转不变性。类似地，若将Fr左乘Es后，可得

ErFrEs=FrAT=ArT

(6)

式中ArFrA。若定义Ar1和Ar2分别为Ar的前M(N-2K-1)行和后M(N-2K-1)行向量组成的矩阵，由式(5)，有

(7)

(8)

若Ψr的特征分解为

(9)

(10)

(11)

由此可知，通过对Ψr特征分解可估计出DOA。

2.2 DOD估计

A′=BA

(12)

其中矩阵B的第i行第j列的元素取值为

(13)

式(3)两边同时左乘B，可得

(14)

为了消除互耦效应，采用与式(6)相同的方法处理式(14)，即定义一个常量矩阵Ft]，并将其左乘式(14)两边，可得

(15)

易验证

(16)

因此

(17)

(18)

上式两边同时右乘Q(见式(11))，得

(19)

(20)

此外，K的取值将直接影响发射天线和接受天线阵列的有效孔径。K值越大，本算法所取得的目标角度估计性能损失越大。

3 仿真结果及实验分析

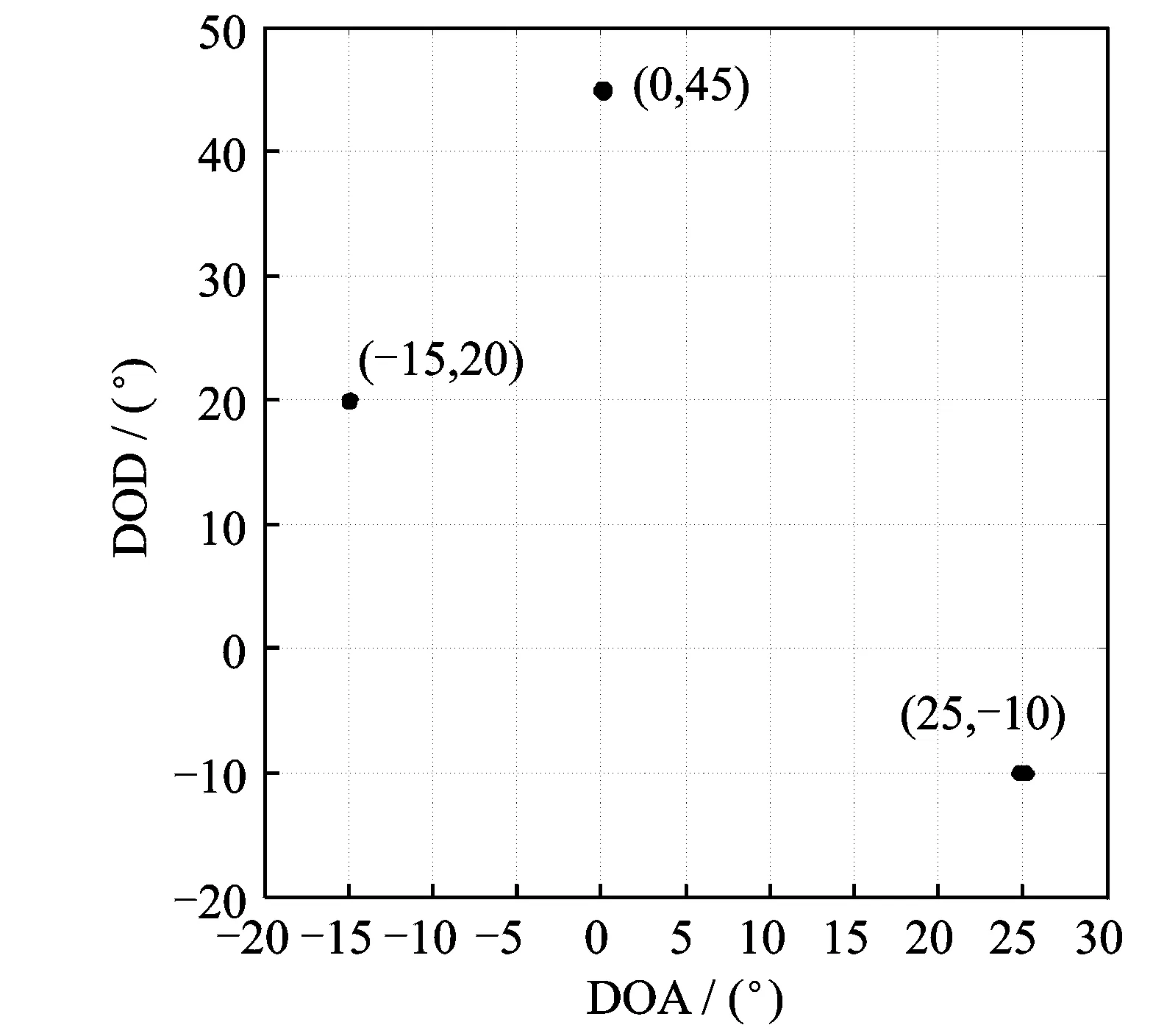
图1 SNR为0时DOD和DOA配对结果 Fig.1 DOD and DOA paired results at SNR=0

图2和图3分别给出了不同算法在K=2时估计DOA和DOD所取得的RMSE随SNR变化的曲线。从各曲线的变化趋势可得以下结果：(1)在未知互耦条件下，原始ESPRIT算法的估计性能受到了较大的影响；(2)文献[17]算法在SNR较低时，目标角度估计性能损失较为严重；(3)本算法在SNR较低时，能取得较好的估计性能，但在SNR较高时，其估计性能不如文献[17]算法。主要原因在于本文考虑的实验条件会使得谱峰搜索的自由度较高，从而导致文献[17]算法在SNR较低时性能损失较大，这也使得该仿真结果与文献[17]给出的结果有所差异。当SNR较高时，谱峰搜索的自由度对算法的影响降低，因此文献[17]算法在角度估计性能上有了较大的提升。另一方面由于本算法在消除互耦效应时丢失了部分接收数据，从而在角度估计性能上相比于使用全部接收数据的文献[17]算法略有不足。

表1 2种算法运行时间的对比结果

图2 不同算法所取得DOA的RMSE随SNR变化曲线图3 不同算法所取得DOD的RMSE随SNR变化曲线Fig.2 RMSE of DOA performance versus SNR amongFig.3 RMSE of DOD performance versus SNR among several methods several methods

4 结束语

本文利用阵列流型矩阵的结构特点和均匀线阵互耦矩阵的带状Toeplitz特性，通过对接收信号的变换和处理来恢复阵列流型矩阵的旋转不变性，以消除互耦效应对目标角度估计性能造成的不利影响，实现在未知互耦条件下基于ESPRIT算法的双基地MIMO雷达系统的DOA和DOD估计。本文算法无需进行谱峰搜索，显著地减小了算法的计算复杂度；同时也实现了目标角度的自动配对，因无需附加额外的角度配对算法，使得算法的计算复杂性进一步降低。仿真实验结果表明，即使在低信噪比情况下，本文算法也具有较好的目标角度估计性能。本文算法存在的一个弱点是：互耦系数自由度K的取值将直接影响本文算法所利用的阵列有效孔径，特别是当K值越大时，本文算法所取得的目标角度估计性能损失越大。

[1] Fishler E, Haimovich A, Blum R S, et al. MIMO radar: An idea whose time has come [C]//Processing of the IEEE Radar Conference. Philadelphia: [s.n.], 2004: 71-78.

[2] Larsson E G, Tufvesson F, Edfors O, et al. Massive MIMO for next generation wireless systems [J]. IEEE Communication Magazine, 2014, 52(2): 186-195.

[3] Stoica P, Li J, Xie Y. On probing signal design for MIMO radar [J]. IEEE Transactions on Signal Processing, 2007, 55(8): 4151-4161.

[4] Lehmann N H, Fishler E, Haimovich A M, et al. Evaluation of transmit diversity in MIMO-radar direction finding [J]. IEEE Transactions on Signal Processing, 2007, 55(5): 2215-2225.

[5] Duofang C, Baixiao C, Guodong Q. Angle estimation using ESPRIT in MIMO radar [J]. Electronics Letters, 2008, 44(12): 770-771.

[6] Zheng G M, Chen B X, Yang M L. Unitary ESPRIT algorithm for bistatic MIMO radar [J]. Electronics Letters, 2012, 48(3): 179-181.

[7] Zheng Z D, Zhang J Y. Fast method for multi-target localization in bistatic MIMO radar [J]. Electronics Letters, 2011, 47(2): 138-139.

[8] Bencheikh M L, Wang Y. Joint DOD-DOA estimation using combined ESPRIT-MUSIC approach in MIMO radar [J]. Electronics Letters, 2010, 46(15): 1081-1083.

[9] Zhang X F, Xu L Y, Xu L, et al. Direction of departure (DOD) and direction of arrival (DOA) estimation in MIMO radar with reduced-dimension MUSIC [J]. IEEE Communications Letters, 2010, 14(2): 1161-1163.

[10]张小飞，张力岑，陈未央，等. MIMO阵列中基于PM和降维变换的高效DOA估计算法[J]. 数据采集与处理，2014, 29(3): 372-377.

Zhang Xiaofei, Zhang Licen, Chen Weiyang, et al. Computationally efficient DOA estimation for MIMO array using propagator method and reduced-dimension transformation [J]. Journal of Data Acquisition and Processing, 2014, 29(3): 372-377.

[11]许凌云，张小飞，许宗泽. 基于圆阵双基地MIMO雷达多维角度联合估计 [J]. 数据采集与处理，2012, 27(3): 279-282.

Xu Lingyun, Zhang Xiaofei, Xu Zongze. Joint multi-angle estimation in bistic MIMO radar based on uniform circular array [J]. Journal of Data Acquisition and Processing, 2012, 27(3): 279-282.

[12]Liu X L, Liao G S. Direction finding and mutual coupling estimation for bistatic MIMO radar [J]. Signal Processing, 2012, 92(2): 517-522.

[13]Ye Z F, Dai J S, Xu X, et al. DOA estimation for uniform linear array with mutual coupling [J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(1): 280-288.

[14]Dai J S, Bao X, Hu N, et al. A recursive RARE algorithm for DOA estimation with unknown mutual coupling [J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13: 1593-1596.

[15]Jinli C, Hong G, Weimin S. Angle estimation using ESPRIT without pairing in MIMO radar [J]. Electronics Letters, 2008, 44(24): 1422-1423.

[16]Leon S J. Linear algebra with applications 6E [M]. Prentice Hall： New Jersey, 2002: 40-49.

[17]郭艺夺，张永顺，张林让，等. 双基地MIMO雷达收发阵列互耦条件下目标定位方法 [J]. 西安电子科技大学学报:自然科学版, 2011, 38(6): 82-88.

Gao Yiduo, Zhang Yongshun, Zhang Linrang, et al. Target localization method for the bistatic MIMO radar in the presence of mutual coupling of receiver and transmitter arrays[J]. Journal of Xidian University:Natural Science, 2011, 38(6): 82-88.

戴继生(1982-)，男，博士，副教授，研究方向：凸优化理论、MIMO无线通信以及阵列信号处理，E-mail：jsdai@ujs.edu.cn。

汪洋(1989-)，男，硕士研究生，研究方向：阵列信号处理，E-mail：young0wang@yahoo.com。

叶中付(1959-)，男，博士，教授，研究方向：阵列信号处理、语音信号处理和图像处理，E-mail：yezf@ustc.edu.cn。

DOA and DOD Estimation for Bistatic MIMO Radar with Unknown Mutual Coupling

Dai Jisheng1， Wang Yang1， Ye Zhongfu2

(1. School of Electrical and Information Engineering, Jiangsu University, Zhenjiang, 212013, China; 2. Department of Electronic Engineering and Information Science, University of Science and Technology of China, Hefei， 230027, China)

A new ESPRIT based direction of departure (DOD) and direction of arrival (DOA) estimation method for bistatic multi-input multi-output (MIMO) radar with unknown mutual coupling is proposed, in connection with the presence of unknown mutual coupling which severely affects the performance of DOA and DOD estimation. The proposed method can estimate the DOA and DOD accurately by utilizing the structural properties of antenna array matrix and the strip feature of mutual coupling matrix of uniform linear array (ULA). Moreover, the new method is free of search with a small amount of calculation. Even in low SNR environment or mutual coupling effect is significant, the performance of the proposed method is also stable. Simulation results illustrate the feasibility and correctness of the proposed method.

array signal processing； multi-input multi-output (MIMO) radar； mutual coupling； direction of arrival (DOA) estimation； direction of departure (DOD) estimation

国家自然科学基金(61102054)资助项目; 中国博士后科学基金(2014M560403,2015T80509)资助项目。

2015-07-28；

2015-10-28

TP274

A