基于基追踪算法的宽带LFM信号信道化侦察*

张剑云 夏 杰 周青松 毛云祥

(合肥电子工程学院,合肥,230037)



基于基追踪算法的宽带LFM信号信道化侦察*

张剑云 夏 杰 周青松 毛云祥

(合肥电子工程学院,合肥,230037)

针对滤波器非理想特性等因素带来的信道化失真对信号侦察的影响，为实现信号参数高精度估计以及波形的准确恢复，提出了基于基追踪算法的宽带LFM信号信道化侦察方法。该方法以l1范数稀疏正则最小二乘模型为目标函数，推导了问题的二阶锥规划(Second order cone programming,SOCP)形式，将各子带输出信号在过完备Gabor原子字典上展开,完成对原信号准确的参数估计与分解重构。仿真实验证明，该方法实现了对信号准确的时频分析与参数估计，通过稀疏原子(较小数据量)准确重构了原宽带信号，并在一定程度上减小信道化失真的影响。

信道化；基追踪；时频分析；参数估计；分解重构

引 言

现代战争中，为实现对各调制样式、带宽的雷达信号全概率接收，多采用数字信道化体制[1-2]。数字信道化接收机将宽带信号划分成多个子带进行处理，尤其是多相体制大大降低数据处理速率实现采样率的转换[3,4]。然而由于滤波器非理想特性等因素[5]以及跨信道处理的问题，信号经信道化后存在失真，影响了对信号的参数估计与分解重构[6-7]。传统的参数估计方法相对较丰富成熟，多以最大似然估计[8]为基础。最大似然估计方法精度高，估计效果逼近克拉美罗界，然而搜索量极大，无法应对现代宽带信号。近年来，诸如分数阶傅里叶变换(FrFT)[9-10]、压缩感知[11-15]等方法被大量应用。由于信号具有稀疏的特性可进行分解，压缩感知理论正是利用这个性质。其中贪婪算法(MP)[13]、正交匹配算法(OMP)[15]计算复杂度低，速度快，然而在精度上有待提高。分数阶傅里叶变换可视为线调基的分解，在不同变换阶数域上进行信号与噪声的分离，然而在不同阶数上存在偏差需进行补偿， 影响了估计精度。基追踪算法(BP)[11,12]具有估计精度高，重构准确以及求解原子具有稀疏性(数据量小)的特点。针对上述问题，结合信道化侦察背景与基追踪算法的优点，本文提出了基于基追踪算法的宽带LFM信号信道化侦察方法。

1 信道化模型与基追踪算法

1.1 信道化模型及仿真

1.1.1 信道化模型

数字信道化接收机模型如图1所示[1]。目标信号x[t](频带范围[fLfH])经高速A/D转换得到离散序列x[n]，再经过K个滤波器组h0[n],…，hk-1[n]滤波，下变频得到基带信号分量uk[n],之后对基带信号进行降速与子带处理。

图1 数字信道化接收机原理图Fig.1 The principle diagram of digital channelized receiver

(1)

经复调制，第k信道带通滤波器为

(2)

其中wk=2πk/K，k=0,1,…,K-1，相应的频率响应为

(3)

1.1.2 仿真结果

本文以8信道复调制滤波器组为模型验证算法(可推广应用于多相结构)。原型滤波器参数通过设置通带波纹rp、阻带衰减rs、过渡带宽及采样率fs得到。设雷达信号为线性调频信号，带宽B=300MHz，中心频率f0=250MHz，调频斜率k=1.17×1015Hz/s。可取fs=2GHz(此处为验证方法而设置)，rp=0.2dB，rs=88dB，过渡带起始频率60MHz，截止频率90MHz。在MATLAB软件中FDATOOL里，设置一定参数可得所需性能的滤波器，其阶数为200阶。原型滤波器幅频特性如图2所示。原型滤波器经复调制后得到的滤波器组幅频特性如图3所示。

图2 原型滤波器Fig.2 The prototype filter图3 复调制滤波器组Fig.3 The complex modulated filter bank

1.2 基追踪算法

1.2.1 过完备字典

在压缩感知理论中，挑选适合的函数作基构建字典十分重要。字典的选择将直接影响求解原子的稀疏性及信号重构的精度。过完备字典指字典中原子个数大于信号维数并包含信号中各向量张成的整个空间。在诸多不同字典中，过完备字典通过增加原子个数来增加系统冗余度，与其他字典相比，增加了对信号逼近的灵活性。本文选择Mallat和Zhang提出的过完备Gabor原子字典[11]。测不准原理指出，有限能量任意信号，其时宽与带宽存在以下关系

(4)

当不等式取等号时，信号为高斯函数e-πt2，具有最小时宽带宽积。Gabor原子为一系列受时间频率调制的高斯函数，其具有最小的时宽带宽积与最好的时频聚集特性。其数学表达式为

(5)

每个Gabor原子通过参数γ=(τ,w,φ)来描述，其中σ为脉冲宽度，τ为脉冲时间中心，w为瞬时角频率，φ为相角。

1.2.2 l1范数稀疏正则最小二乘模型

本文将信号在过完备字典上进行展开，通过基追踪算法求解稀疏原子，最后完成对原信号的重构。鉴于此思想，将信号模型进一步构建为基于混合l0范数的稀疏正则最小二乘模型

(6)

式中‖Ax-y‖2代表数据的拟合误差，γ‖y‖0代表Gabor原子向量稀疏度的衡量，γ是加权因子，它实现对数据的拟合质量和原子向量稀疏度的平衡与折中，从而兼顾两者的性能。

式(6)中包含了l0范数的优化问题，这是一个整数优化的NP难问题，现有理论难以给出一个有效的求解方法。因此可对该问题进行转化，将其松弛为能有效求解的凸优化问题。由于l1范数是在所有lp范数(‖·‖p,p≥1)当中最接近l0范数的凸范数，因此将上述模型进一步松弛为混合l1范数的稀疏正则最小二乘模型[4]

(7)

因此如何求解该模型是本问题的难点所在。一般优化方法难以求解优化模型中的目标函数。因为其为两个不可微函数的混合。但是该模型很明显是凸优化问题，因此考虑将其转化为二阶锥规划(Second-orderconeprogramming，SOCP)问题，用原对偶内点算法进行有效求解，则所获解一定为该优化模型的全局最优解。

1.2.3 l1范数稀疏正则最小二乘模型的求解

将标准的k维二阶锥记为

(8)

(9)

(10)

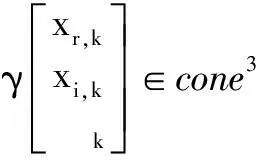
(11)

(12)

至此可以构造出式(7)的SOCP模型为

minimize vTw

(13)

对于式(13)可以采用MatLab中的CVX工具箱进行求解。

2 基于基追踪算法的宽带LFM信号信道化侦察

2.1 参数估计原理

测不准原理指出，Gabor原子具有良好的时频聚集特性。将信号分解为Gabor原子的线性组合，则可以清楚地分析信号的时频特征。假设信号y经稀疏分解为k个Gabor原子，这k个原子f(τi,wi,φi)|i=1,2，…，k包含了原信号的特征以及绝大部分的能量。对这k个原子进行时频分析，进而可提取出其中的参数信息。图4为包含三分量线调信号时频图(右侧为频域图，下方为时域图)，它由文献[11]中MP算法在Gabor字典上分解的原子经Wigner变换排列所得。可见，属于同一个线调信号的原子排列在同一条直线上，直线显示了信号频率随时间的变化，直线的斜率即为该线调信号的调频斜率。而直线两端的两个原子分别表示起止和终止频率。因此通过提取Gabor原子中包含的时频位置信息，可求得信号的频率信息。

图4 文献[11]中三分量线调信号时频图Fig.4 The time-frequency diagram of three-component line FM signal in Ref.[11]

2.2 算法步骤

基于基追踪算法的宽带LFM信号信道化侦察，最重要的环节是对子带输出信号进行处理，求解出稀疏向量x。后续对整个信号的调频斜率、起止频率的估计以及稀疏重构都是围绕稀疏向量x展开。具体步骤如下。

(1)求解稀疏向量xi。对存在信号的i子带输出进行处理，利用CVX工具箱求解问题的SOCP形式。在此处理过程中，设置适当门限，挑选稀疏向量xi。

(3)调频斜率估计。各子带筛选的稀疏原子按参数(τi,wi)作时频图并按照各自信道的先后顺序衔接在一起。观察可以看出各原子所在点的排布呈一条直线状。经最小二乘线性估计可知，该直线的斜率即为信号的调频斜率。

(4)起止频率估计。在时频图中挑选出中心时间最大、最小的点，对起始终止频率进行估计。

3 仿真实验

取信号幅度a0=1，初始频率f1=100MHz，选取采样点数N=512，脉冲宽度PW=2.56×10-7s，脉内调制带宽B=300MHz，脉冲调制斜率μ0=1.17×1015Hz/s，采样频率fs=2GHz。噪声w(t)为加性高斯白噪声，选取信噪比SNR=10dB。

3.1 信号及各信道输出

3.1.1 信号仿真

图5为本文原始信号的时域波形与幅频特征。

图5 本文原始信号的时域波形与幅频特征Fig.5 The waveform and frequency spectrum of original signal in this paper

3.1.2 各子带输出波形与频谱

图6从左到右，上到下依次为h0,h1,…,h78个信道输出信号的时域与频谱图。从图中可以看到，第1,2,3信道有信号输出，即目标信号带宽跨越3个信道。故对信道1,2,3输出信号进行子带处理即可。

3.1.3 未经算法处理信号

不经本文算法处理，将图6中h1,h1,h2这3个信道的滤波信号按滤波器所滤频带位置简单拼接，不作处理，重构信号波形及幅频特征如图7所示。

图6 各滤波器输出Fig.6 The output of each filter

图7 未经算法处理的信号波形和频谱Fig.7 The waveform and frequency spectrum of signal without algorithm processing

与图5进行比较，图7中经滤波后拼接的信号滤除了带外的噪声，信号的幅频特征因为受滤波器幅频特性的调制，带宽内起伏波动较大，明显存在较高的两处尖峰，正是滤波器之间交叠处。

3.2 子带基追踪算法仿真

信道1输出经基追踪算法处理得33个稀疏原子，斜率估计1.172×1015Hz/s。波形的稀疏表示与时频分布分别如图8(a)和(b),其中时频图中直线为真实斜率。信道2输出经基追踪算法处理得30个稀疏原子，斜率估计1.112×1015Hz/s,波形的稀疏表示与时频分布分别如图9(a)和(b)。

图8 信号稀疏表示和Gabor原子时频分布(信道1)Fig.8 Sparse representation of the signal and time-frequency distribution of Gabor atoms(Channel 1)

图9 信号稀疏表示和Gabor原子时频分布(信道2)Fig.9 Sparse representation of the signal and time-frequency distribution of Gabor atoms(Channel 2)

信道3输出经基追踪算法处理得24个稀疏原子，斜率估计1.172×1015Hz/s。波形的稀疏表示与时频分布分别如图10(a)和(b)。

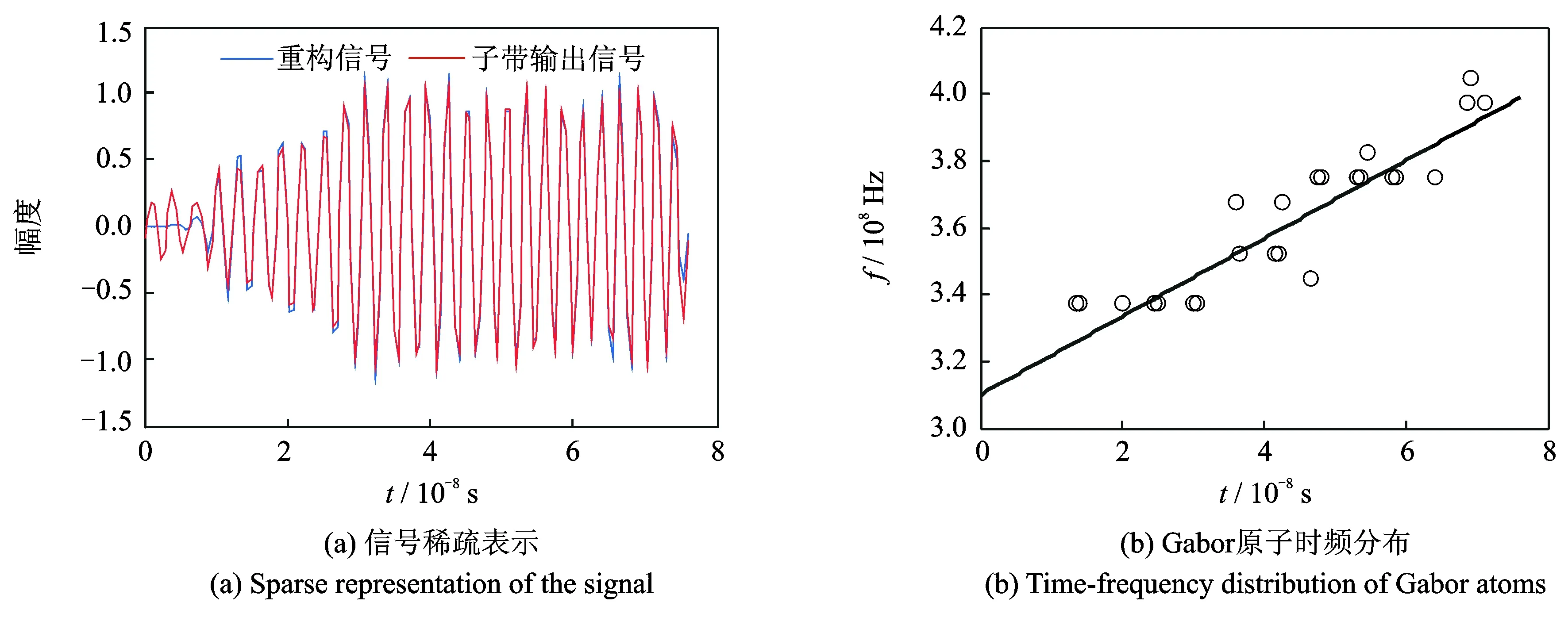
图10 信号稀疏表示和Gabor原子时频分布(信道3)Fig.10 Sparse representation of the signal and time-frequency distribution of Gabor atoms(Channel 3)

3.3 子带处理信号合成原信号

根据3个信道的中心频率等先验信息，将下变频后信号调整恢复到原信号相应位置，重构原信号的时频信息如下。从图11看出，经本文算法处理，原信号通过87个稀疏原子(较少的数据量)很好地被稀疏表示重构。信号的调频斜率估计为1.158×1015Hz/s，与真实值相差0.012×1015Hz/s。第一个与最后一个Gabor原子的频率分别为1.013×108Hz和3.975×108Hz。即信号起始与终止频率分别为1.013×108Hz和3.975×108Hz，与真实值相差0.013×108Hz和0.025×108Hz。

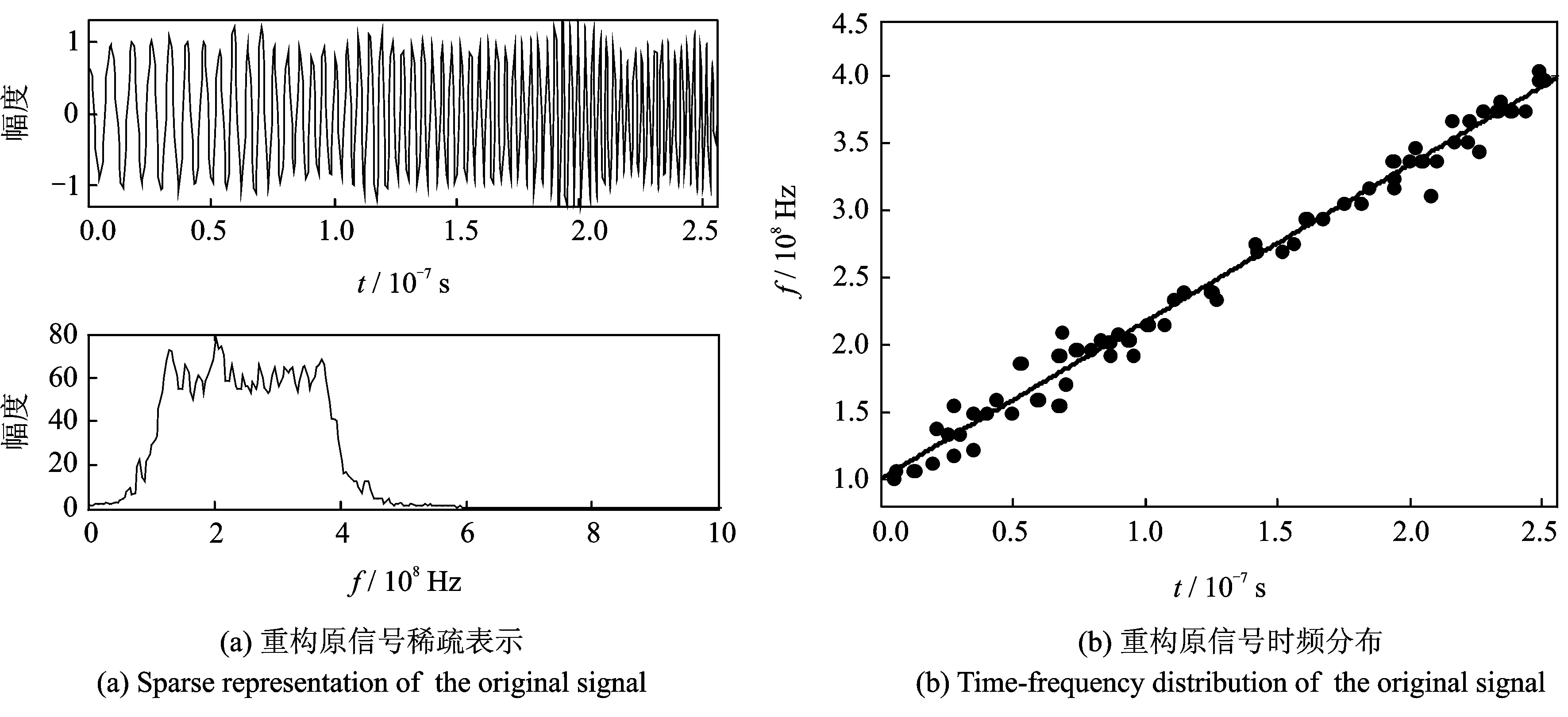
图11 重构原信号稀疏表示和时频分布Fig.11 Sparse representation of the original signal and time-frequency distribution of the original signal

3.4 效果对比

图12 频谱图比较Fig.12 Comparision of spectrogram

本文算法在完成对信号参数估计与时频分析的同时，实现了对各子带信号的分解与原信号的重构。重构情况如图12所示。从图12看出，经滤波未经处理的信号通带内两处凸起正是受滤波器之间交叠处影响。而本文算法在处理过程中缓和了滤波器交叠处的影响，减小了信道化失真，重构信号带宽内较平缓。经计算，经本文算法得到信号与原信号相似度0.96，而未经处理信号为0.88,从而验证了本文算法的有效性。

4 结束语

本文将基追踪算法引入对宽带信号的参数估计、时频分析和分解重构，以l1范数稀疏正则最小二乘模型为目标函数并推导了问题的SOCP形式。仿真分析表明,本文算法筛选的Gabor原子稀疏性好，有助于降低存储的数据量；实现对原信号参数高精度估计和时频特征准确分析；同时实现了对原始信号准确的重构恢复，并在一定程度上减小了信道化失真的影响。

[1] James Tsui. 宽带数字接收机[M]. 北京：电子工业出版社，2002．

James Tsui. Wideband digital receiver[M]. Beijing:Electronic Industry Press,2002.

[2] 杨小牛,楼才义,徐建良.软件无线电技术与实现[M].北京:电子工业出版社，2004.

Yang Xiaoniu, Lou Caiyi, Xu Jianliang. Software defined radio enabling technologies[M]. Beijing:Electronic Industry Press,2004.

[3] 秦文兵,罗来源,叶中付. 一种基于多相带通结构的信道化滤波器算法[J].数据采集与处理,2006,21(2):133-136.

Qin Wenbing, Luo Laiyuan, Ye Zhongfu. Channel filter algorithm based on polyphase structure with bandpass filters[J]. Journal of Data acquisition and Processing, 2006,21(2):133-136.

[4] 付永庆,李裕.基于多相滤波器的信道化接收机及其应用研究[J].信号处理,2004,20(5):517-520.

Fu Yongqing, Li Yu. The realization of channelized receivers based on polyphase filters[J].Signal Proceeding, 2004,20(5):517-520.

[5] 罗胜恩,罗来源,苑小华,等. 频域滤波算法的幅相失真及抑制方法[J].数据采集与处理,2010,25(S):51-54.

Luo Shengen, Luo Laiyuan, Yuan Xiaohua,et al. Analysis and suppression of amplitude-phase distortion for frequency domain filtering algorithm[J]. Journal of Data Acquisition and Processing, 2010,25(S):51-54.

[6] 冀连营,高梅国,李云杰. 跨信道检测仲裁的信号集合更新算法[J].北京理工大学学报,2009,29(6):532-535.

Ji Lianying, Gao Meiguo, Li Yunjie. Signal collection update algorithm for cross channel detection and arbitration[J]. Transactions of Beijing Institute of Technology,2009,29(6):532-535.

[7] 王阳,徐忠伟,程嗣怡.容差判决和参数估计结合解决信道化接收机跨信道问题[J].空军工程大学学报:自然科学版,2015,16(2):61-66.

Wang Yang, Xu Zhongwei, Cheng Siyi. Elimination of Cross-channel problem in channelized receiver through tolerance judgment and parameter estimation[J]. Journal of Air Force Engineering University: Natural Science Edition, 2015,16(2):61-66.

[8] 张容权, 杜雨洺,杨建宇,等.一种LFM信号最大似然估计模型与参数估计快速算法[J]. 电波科学学报,2005,20(5):651-655.

Zhang Rongquan, Du Yuming, Yang Jianyu, et al. Maximum likelihood estimation model and parameter fast estimation algorithm of LFM signal[J]. Chinese Journal of Radio Science, 2005,20(5):651-655.

[9] 袁振涛，胡卫东，郁文贤.用FrFT插值实现LFM信号的参数估计[J].信号处理，2009,25(11):1727-1731.

Yuan Zhentao, Hu Weidong, Yu Wenxian. Parameter estimation of LFM signals using FrFT interpolation[J].Signal Processing, 2009,25(11):1727-1731.

[10]齐林，陶然. 基于分数阶Fourier变换的多分量LFM信号的检测和参数估计[J].中国科学E辑:技术科学，2003,33(8);749-759.

Qi Lin, Tao Ran. Multi-component LFM signal detection and parameter estimation based on fractional Fourier transform[J]. Science in China(Series E), 2003,33(8);749-759.

[11]Stephen Boyd, Lieven Vandenberghe. Convex optimization[M]. 北京：清华大学出版社，2013.

[12]芮国胜,王林,田文飚. 一种基于基追踪压缩感知信号重构的改进算法[J].电子测量技术，2010,33(4):38-41。

Rui Guosheng, Wang Lin, Tian Wenbiao. Improved algorithm based basis pursuit for compressive sensing reconstruction[J]. Electronic Measurement Technology, 2010,33(4):38-41.

[13]Mallat S G, Zhang Z F. Matching pursuit with time-frequency dictionaries[J].IEEE Trans on Signal Processing, 1993,41(12):3397-3415.

[14]闫浩,董春曦,赵国庆. 基于压缩感知的线性调频信号参数估计[J].电波科学学报,2015,30(3):449-454.

Yan Hao, Dong Chunxi, Zhao Guoqing. Parameter estimation of LFM signal based on compressed sensing[J]. Chinese Journal of Radio Science, 2015,30(3):449-454.

[15]Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007,53:4655-4666.

张剑云(1963-),男,教授，博士生导师，研究方向：雷达信号处理，高速数字信号处理，E-mail：krwang@mail.hf.ah.cn。

夏杰(1991-)，男，硕士研究生，研究方向：宽带雷达信号侦察与干扰，E-mail：xj_eei@163.com。

周青松(1982-),男,讲师，博士，研究方向：雷达信号处理。

毛云祥(1973-),男,讲师，研究方向：信号与信息处理。

Channelized Detection of WLFM Signal Based on Basis Pursuit

Zhang Jianyun, Xia Jie, Zhou Qingsong, Mao Yunxiang

(Electronic Engineering Institute of PLA, Hefei, 230037, China)

The non-ideal properties of a filter lead to channelization distortion, which affects signal detection. In order to achieve high precision signal parameters estimation and waveform recovery accurately, a method of channelized detection of WLFM signal based on basis pursuit is presented. The method usesl1norm sparse regular least squares model and deduces the SOCP form of the model. It expands the output signals of each subband over complete Gabor atom dictionary and achieves the parameter estimation and decomposition and reconstruction of the original signal. Simulation results show that the proposed method realizes the accurate time-frequency analysis and parameter estimation of the signal, reconstruct original wide band signal through sparse atoms (less data) and reduces the impact of channelization distortion to some extent.

channelization; basis pursuit; time-frequency analysis; parameter estimation; decompositionreconstruction

国家自然科学基金(11375263)资助项目。

2016-06-01；

2016-07-02

TN911.72

A