高分辨率极化合成孔径雷达成像研究进展*

朱岱寅 杨鸣冬 宋 伟 叶少华

(1.南京航空航天大学电子信息工程学院，雷达成像与微波光子技术教育部重点实验室，南京，211106； 2.中航工业雷华电子技术研究所，无锡，214063)



高分辨率极化合成孔径雷达成像研究进展*

朱岱寅1杨鸣冬1宋 伟2叶少华2

(1.南京航空航天大学电子信息工程学院，雷达成像与微波光子技术教育部重点实验室，南京，211106； 2.中航工业雷华电子技术研究所，无锡，214063)

合成孔径雷达(Synthetic aperture radar，SAR)是一种有效的地球遥感技术，对观测区域进行全天时、全天候的高分辨率大范围成像，在军事侦察、环境监测和地质测绘等领域有着十分广泛的应用。随着雷达技术和地球科学的发展，人们期望能够获取更多的目标特性，传统的单极化SAR已经难以满足越来越多元化的实际应用需求。极化合成孔径雷达(Polarimetric synthetic aperture radar，PolSAR)基于多个极化通道获取目标不同极化状态下的散射特性丰富了SAR图像的信息量，拓展了SAR的应用领域。从极化数据中准确地解译目标的物理特性是PolSAR应用的重要前提。本文对PolSAR的研究进展进行了总结，重点介绍了极化目标分解算法，给出了高分辨率PolSAR实测数据处理结果，并对未来研究方向进行了展望。

极化合成孔径雷达；雷达成像；极化目标分解；散射机理；散射模型

引 言

合成孔径雷达(Synthetic aperture radar，SAR)作为一种先进的航空、航天微波遥感手段，能够提供观测区域的高分辨率二维图像，在灾害监测、海洋观测、环境保护、资源勘查、精细农业、地质测绘以及城市规划等方面有着十分广泛的应用[1-6]。SAR基于飞机、卫星等雷达平台的运动，通过信号处理的方法获取二维高分辨率，在本质上是唯一可以实现高分辨率的成像雷达技术。SAR的传感器是能够穿透云、雾、雨和尘等物质的主动式微波辐射源，无须依赖太阳光源，从而具备全天时、全天候的全球范围对地成像能力。随着越来越多机载、星载SAR系统的投入使用，SAR在对地观测领域展现出卓越的能力和不可或缺性，目前已经成为高分辨率对地观测和全球资源管理最重要的手段之一。

自20世纪50年代理论的提出以来，经过数十年的发展，合成孔径雷达已经取得了众多举世瞩目的成果。SAR系统的早期应用中，主要是以军事侦察和人造目标探测为目的，SAR图像仅仅能够表征目标的散射系数。随着分辨率越来越高，SAR系统已经不再满足于只是获得观测区域的二维灰度图像。同时，雷达技术、地球物理学参数反演模型的不断发展，为SAR更广泛的应用提供了理论基础。因此，在高分辨率成像处理技术不断改进的同时，SAR对目标物理特性的解译能力也需要进一步提高。SAR的早期研究主要是依靠引入各种新技术，目前及未来的发展则逐渐转变为由各种应用需求来推动，提高图像所包含的信息量，增强系统获取目标特征的能力。其中极化雷达遥感技术获得了前所未有的关注和投入，是当前研究的热点，近年来发射和计划发射的星载SAR都具有极化能力。主要以国外的雷达系统为代表，例如日本JAXA的ALOS-1，ALOS-2，加拿大CSA/MDA的RADARSAT Constellation Mission，德国DLR/Astrium的TerraSAR-X，Tandem-L，以及欧洲ESA的Sentinel-1和BIOMASS。

极化合成孔径雷达(Polarimetric synthetic aperture radar，PolSAR)在SAR的基础上引入电磁学中的极化理论，拓展了SAR的应用领域。PolSAR通过分析散射电磁波中所包含的极化信息，以获取目标的散射特性，实现参数的精确反演。相比于传统单极化SAR，全极化SAR具有以下优势：(a)全极化SAR能够获取更加丰富的目标散射信息，从而可以估计相关物理参数，例如几何形状、材料构成、湿度、粗糙度以及定向角等；(b)极化信息处理提取目标的极化特征，降低了雷达波段、观测角度等因素对目标检测的影响，增强了目标的识别分类性能；(c)单极化SAR由于电磁波极化状态固定，并不能对所有类型的目标都能取得较好的观测效果，全极化SAR通过不同的收发极化状态对不同散射特性的目标进行更灵活的观测；(d)全极化SAR能够选取收发极化组合，以获取目标散射电磁波的最优接收，提高系统抗干扰和杂波抑制的能力。PolSAR技术在军事、农业、林业、海洋以及地质等方面存在重要的应用潜力和价值[7-14]：(a)极化信息能够反映农作物的多种物理特性，农作物的散射特性通常会随着生长而发生变化，并且不同农作物的散射特性之间也存在差异，PolSAR图像可以用于监测农作物的生长情况，对不同农作物进行分类；(b)森林植被等一直是PolSAR应用研究中的重要领域，研究人员致力于利用极化信息进行森林生物量估计和植被种类识别，极化干涉SAR同时引入干涉测量技术，基于地表和随机体散射模型(Random volume over ground，RVoG)能够进一步提高森林高度估计和植被分类的精度；(c)PolSAR对于海洋遥感的研究主要针对海浪、洋流和海面活性物质，有效进行海洋表面坡度测量、方位海浪坡度谱测量以及海流引起的表面特征测量，PolSAR图像增强了雷达海洋探测的能力；(d)地表粗糙度和土壤湿度是地质研究中的关键参数，传统雷达回波受粗糙度、波长和地表介电常数等因素的影响，难以精确估计地表特征参数，PolSAR增加的测量信息使得地表粗糙度和土壤湿度对雷达回波的影响区分开来，从而提高估计精度，同时PolSAR图像还常用于灾害监测和损失评估。国内外研究人员对极化信息的处理和应用做了大量有意义的工作，本文对这些研究工作进行了总结。

1 高分辨率SAR成像处理概述

对于极化合成孔径雷达来说，极化信息处理的重要前提是SAR信号处理，获得聚焦良好的高分辨率图像。因此，本文首先对高分辨率SAR成像处理做一个简单介绍。SAR作为一种广泛应用的遥感手段，根据不同观测需求，可以按不同模式工作，从经典的条带(Stripmap)、聚束(Spotlight)和扫描(Scan)，到新兴的滑动聚束(Sliding spotlight)、TOPS(Terrain observation by progressive scans)以及延伸的逆SAR(Inverse SAR，ISAR)、双基SAR(Bistatic SAR)和干涉SAR(Interferometric SAR，InSAR)等。经过数十年的发展，研究人员提出了一系列优秀的成像处理算法，获取二维高分辨率。距离多普勒算法(Range Doppler algorithm，RDA)[4]是最简单的精确成像处理技术，对距离向和方位向分别进行匹配滤波，高效实用；但是二次距离压缩(Second range compression，SRC)是处理中的一个难点，严重影响高分辨率情况下的聚焦效果。Chirp Scaling算法(Chirp scaling algorithm，CSA)[15]基于尺度变换原理对线性调频(Chirp)信号进行处理，距离徙动校正(Range cell migration correction，RCMC)的插值操作可以通过傅里叶变换和复数乘法来实现，降低了运算量；CSA忽略了SRC的距离空变性，并且使用了信号距离多普勒域的近似形式，在大斜视角、大场景成像时会产生严重的散焦，扩展CSA(ECSA)[16]、分数阶CSA(FrCSA)[17]、非线性CSA(NCSA)[18]等进行了改进，以适用更多的场景。Frequency Scaling算法(Frequency scaling algorithm，FSA)[19]将尺度变换原理应用于去斜率(Dechirp)信号，完成频域信号变标处理。Omega-K算法(Omega-K algorithm，OKA)[20,21]又称为距离徙动算法(Range migration algorithm，RMA)，基于信号二维频谱的精确表达形式，没有任何近似，是一种十分理想的成像算法，适用于各种场景的成像处理，精度高；但是核心步骤Stolt插值运算量较大，影响了OKA的处理效率。极坐标格式算法(Polar format algorithm，PFA)[3,22]主要应用于聚束SAR成像，适用于成像场景较小的情况；核心步骤二维插值需要耗费较大的运算量，并且需要进行额外的波前弯曲校正。除了上述频域成像算法，还有典型的时域成像算法——后向投影算法(Back projection algorithm，BPA)[23]，及其改进算法快速BPA，其需要对每个像素点进行相干积累成像，运算代价很高。

上述成像算法的提出都是假设雷达运载平台匀速直线运动，忽略了实际情况中平台的不规则运动引起的航迹误差。由于SAR 是相干成像系统，回波信号相位的精度决定了最终的图像质量。星载SAR中，运动误差对于成像处理的影响不大，通常可以忽略。机载SAR中，即使微小的运动误差都会引起较大的相位误差，在某种程度上对分辨率、几何线性度和对比度等产生影响，从而导致图像聚焦质量明显下降。因此，运动补偿是机载SAR数据处理中的关键步骤。特别是随着分辨率不断提高，合成孔径时间较长，运动误差引起的图像散焦现象更加严重。目前，常用的运动补偿方法有两类：基于运动测量数据的运动补偿和基于回波数据的运动补偿。基于运动测量数据的运动补偿算法的代表是一步运动补偿法[24]和两步运动补偿法[16]，通过包络补偿和相位补偿两个步骤对信号中的误差进行校正。由于运动误差的距离空变性，包络补偿需要通过插值操作将信号校正到正确的距离单元，运算量较大；算法补偿效果受运动测量数据精度的影响较大，而高精度的运动参数测量设备通常成本较高。基于回波数据的运动补偿算法又称为自聚焦算法，利用参数估计技术从信号中估计载机的运动参数信息或运动误差引起的相位误差信息。优点是补偿精度高，几乎不需要额外的硬件成本；缺点是实现复杂，处理效率低。典型的自聚焦算法有子孔径偏移算法(Map drift，MD)[25]、秩一相位估计算法(Rank one phase estimation，ROPE)[26]和相位梯度自聚焦算法(Phase gradient autofocus，PGA)[27]。由于上述传统自聚焦算法是基于聚束模式提出的，直接应用于条带模式效果并不理想。针对条带模式与聚束模式的差异，研究人员进行了改进，其中具有代表性的是PGA-MD算法[28]。该算法结合两种自聚焦算法的特点，利用相邻子图像间方位向偏移量和线性相位之间的关系，计算线性相位差，并基于一阶导数实现子孔径相位误差函数拼接，能有效减小子孔径相位误差函数拼接过程中引入的误差，提高对条带SAR图像的自聚焦效果。

综上所述，要想获取聚焦良好的成像结果，需要结合多种关键处理技术。本文简要介绍了在机载SAR实测数据处理中一套行之有效的成像处理流程，该流程兼顾聚焦效果和处理效率，具有很好的实用价值。核心成像算法选择Omega-K算法，因为其是一种精度较高的理想成像算法；此外，该算法能够首先完成距离向脉压，后续处理时可以对数据距离向划分子带，针对距离向测绘带较宽的情况合理匹配运算资源，提高处理效率。运动补偿采用多级处理的方法，将基于运动测量数据的运动补偿与基于回波数据的运动补偿结合起来，以获取更好的效果。首先是基于运动测量数据的运动补偿，因为距离向脉压已经完成，所以一步运动补偿法更加适用于Omega-K算法；同时结合距离子带对一步运动补偿法的流程进行改进，对于单个距离子带来说，运动误差的距离空变性有所降低，可以近似为子带中心距离单元的运动误差，包络补偿就可以用复数乘法代替运算量较大的插值，实现快速近似包络补偿；为了保证相位精度不受影响，推导了运动误差的另一种表达式，改进了相位补偿，从而能够在包络补偿前完成相位补偿；快速近似包络补偿可以在Omega-K算法中的一致压缩步骤进行，不再需要一个单独步骤，进一步简化了处理流程。自聚焦算法对Omega-K算法处理后的数据进行处理，补偿残余运动误差。完整的数据处理流程如图1所示。

图1 高分辨率机载SAR成像处理流程Fig.1 Flow diagram of high resolution airborne SAR imaging

2 极化合成孔径雷达概述

随着SAR技术的不断发展，传统单极化SAR获取的电磁信息难以全面反映目标散射特性。极化合成孔径雷达作为一种应用十分广泛的微波遥感技术，一般通过两个通道发射和接收特定极化状态的电磁波，所测得的4组极化数据可以构成一类完备的极化基集，从而获取完整的极化信息。极化信息不仅包含散射功率信息，各通道间的相对相位信息还可以反映目标散射特性的差异。PolSAR在SAR的基础上引入电磁学中的极化理论对获取的极化信息进行处理，能够增强SAR解译散射机理的能力，精确反演目标参数(如材料、形状、粗糙度和定向角等)，在非监督地物分类、目标检测和识别以及地物参数估计方面存在重要的应用潜力和价值。PolSAR图像最直接的应用体现在其能够更加精细地反映目标的细节特征，尽管目前的SAR系统已经能够获得比较高的分辨率，但雷达回波作为多种散射机理的集合，令目标特征的解译仍然存在巨大的挑战。PolSAR通过分析不同散射机理的极化信息，从而识别更精细的目标特征。Lee等通过处理丹麦Great Belt大桥C波段的全极化数据，得到桥梁建设过程中不同阶段的极化图像，提取出桥梁各个部分的散射特征，展示了PolSAR在分析人造建筑物目标特征时表现出的优越性能[7]。其次，PolSAR图像包含更多的测量信息，扩展了目标的观测维度，提取出的极化参数能够反映更多的目标散射特征，地表粗糙度和土壤湿度的估计、森林高度估计、冰川监控以及海洋参数测量等都是PolSAR图像的主要应用领域。

为了便于分析极化合成孔径雷达的应用，首先介绍常用的参量。对于PolSAR，Sinclair提出了极化后向散射矩阵的概念[29]

(1)

式中：矩阵的4个元素表示复散射系数或复散射幅度，下标H，V分别表示水平极化和垂直极化，对应于接收和发射的极化状态。本文主要讨论单站后向散射的情况，在此条件下，满足互易性假设的散射矩阵为对称矩阵，即SHV=SVH，Pauli特征矢量可以表示为

(2)

Lexicographic特征矢量可以表示为

(3)

基于上述两组特征矢量，可以得到描述目标散射特性的两个重要物理量。3×3极化相干矩阵由Pauli特征矢量与自身共轭的向量外积的统计平均得到

(4)

式中：〈·〉表示对数据求时间或空间的统计平均，主要针对分布式目标的情况。3×3极化协方差矩阵则由Lexicographic特征矢量与自身向量外积的统计平均得到

(5)

对于单一散射目标，其极化散射特性可以完全由式(1)的散射矩阵表示。分布式目标可以认为由大量随机分布的单一散射目标构成，观测的散射矩阵是由各独立的散射机理相干叠加而成，无法由等价的单一散射目标表示。因此，式(4)和式(5)中的二阶统计量可以对分布式目标进行更全面、更精确的分析，PolSAR的大量研究也是基于极化相关矩阵或协方差矩阵进行。此外，在目标分类、参数反演等实际应用中还会使用不同极化通道之间的复相关系数

(6)

式中SRR和SLL分别表示圆极化基下的右旋圆极化散射系数和左旋圆极化散射系数，能够表示为线极化基下的散射系数的线性组合。

经过数十年的发展，研究人员进行了大量有关极化雷达应用的研究。极化合成孔径雷达的研究涉及电磁波散射理论、多通道相干雷达系统及数据处理技术以及目标物理参数反演等，是基础理论与实验科学紧密结合并相互促进的典型研究领域之一，主要研究进展归纳如下。

(1)极化信号自身特性

与其他科学研究类似，研究人员首先对极化信号、极化数据的自身特性进行了深入研究，如最优极化增强、极化数据的统计特性等。最优极化讨论的是如何选取收发极化组合，以求解目标散射电磁波的最优接收功率问题。Kostinski和Boerner研究了任意发射极化状态下的最优接收功率问题[30]；Ioannidis和Hammers讨论了杂波环境下如何获得最大的雷达信号强度，利用最优极化辨别杂波和目标[31]；杨健等提出了相对最优极化的概念[32]，基于数值计算的方法求解各种收发极化组合情况下的相对最优极化问题；杨健等还提出了极化相似性的理论[33]，进一步提高抗干扰和杂波抑制的能力，并结合极化散射熵研究了广义相对最优极化问题[34]。最优极化理论使得杂波抑制可以在极化域实现，在抗干扰、极化增强和极化图像分类等方面有着广泛的应用。王雪松等以瞬时极化信号理论为思路，在极化成像及干扰抑制等方面也作出了重要贡献[35-37]。

关于极化数据统计特性的研究，以散射矩阵、相干矩阵和协方差矩阵的概率密度问题为主。研究表明复散射系数的幅度满足瑞利概率密度分布，相位满足均匀概率密度分布[38]；均匀区域目标特征矢量满足零均值复高斯分布，非均匀区域目标特征矢量满足K分布[39]；极化相干矩阵和协方差矩阵满足复Wishart概率密度分布[40]。研究极化数据的统计特性能更有效地设计相干斑滤波、目标分类和目标检测等算法，同时需要针对实际观测数据的散射特性优化统计方法。

(2)SAR图像相干斑滤波

SAR图像由于其成像原理，不可避免地受到相干斑噪声的影响。相干斑噪声增加了图像解译的难度，需要对PolSAR图像进行相干斑滤波，以使得极化数据的分析更加精确。均值滤波和中值滤波等常用的滤波技术虽然能有效降斑，但是目标细节特征损失较严重，造成边缘和特征模糊，并且缺乏自适应性。Lee使用乘性噪声模型描述相干斑的特性，提出了基于最小均方误差的Lee滤波器[41]，利用局部均值和局部方差进行相干斑滤波，因此又称为局部统计特性滤波器。为了保持边缘特征，Lee提出了基于边界对齐窗的改进Lee滤波器[42]，不再使用简单的正方形窗选取邻近像素，而是采用方向与边缘方向相同的非正方形窗。基于局部统计特性的相干斑滤波算法还有很多改进[43-45]，如Kuan滤波、Frost滤波、sigma滤波和最大后验概率(Maximum a posteriori，MAP)滤波等。同时还与一些新兴理论结合[46]，如基于场景结构模型、模拟退火等。上述滤波算法没有对相干矩阵或协方差矩阵中的非对角线元素进行合适的滤波，无法保留原始的极化信息。Goze和Lopes使用上述滤波器对协方差矩阵的非对角线元素进行处理[47]；Novak和Burl提出了极化白化滤波器(Polarimetric whitening filter，PWF)[48]，通过最优地组合协方差矩阵的所有元素，能够对全极化数据进行滤波；Lopes和Sery基于纹理模型和乘性噪声模型，提出了针对纹理变化的相干斑滤波算法[49]。

(3)极化目标分解算法

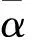
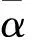
(4)极化目标分类算法

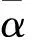
(5)极化目标检测算法

目标检测一直是雷达技术应用中的一个重要研究方向。经典的目标检测大多基于统计方法，Chaney，Novak等提出一系列基于统计方法的极化目标检测技术，如极化白化滤波器、最优极化检测器(Optimal polarimetric detector，OPD)、单位似然比检验(Identity likelihood ratio test，ILRT)等[78-81]。基于统计方法的目标检测往往缺乏物理基础，PolSAR由于其本身的系统设计，可同时提供目标在多个极化通道的信息，因此极化目标检测应充分利用更多的目标散射信息。极化目标检测衍生出另一类基于物理方法的目标检测算法，该类算法在初始阶段可以利用目标的极化散射特性进行检测，在后续处理时再结合统计方法进一步提高检测能力。Lee等基于极化通道间的复相关系数[82,83]，分析了不同散射特性目标的复相关系数的差别，提高了人造目标与自然目标的区分能力。文献[33]中的极化相似性参数可用于估计目标的散射类型、几何结构，文献[34]结合极化散射熵、各极化通道功率和相似性参数，能够有效进行道路检测和水面目标检测。此外，研究人员提出了一系列方法来检测识别雷达图像中的典型军事目标[84-87]，尤其是关于舰船目标检测的应用最为广泛。

极化数据处理的主要流程如图2所示。极化目标分解可以看作是一个定性处理的步骤，得到观测区域的伪彩色合成图像，直观展示目标散射特性；目标检测、目标分类和参数反演等则可以认为是定量应用，利用目标分解得到的散射特征参数进行处理。

图2 极化数据处理流程Fig.2 Flow diagram of polarimetric data processing

3 极化目标分解的基本原理

对于实测数据来说，极化后向散射信号通常可以看作是不同的基本散射机理的叠加。常用的基本散射机理有表面散射、二次散射和体散射等。极化目标分解的主要任务是将测量的极化散射矩阵分解为基本散射机理的求和形式，根据不同散射机理所占权重确定目标的散射特性，获取相关物理参数。极化目标分解理论已成功应用于多种领域，如地表目标检测和分类、土壤湿度估计、森林勘探、海洋遥感和环境监测等。经过数十年的发展，研究人员相继提出了众多优秀的极化目标分解算法。根据前文的介绍，PolSAR数据可以表示为不同的矩阵形式，从最基本的后向散射矩阵S，到二阶统计量极化相干矩阵T和协方差矩阵C。根据处理的矩阵形式，分解算法可以分为两大类：相干分解和非相干分解。主要的极化目标分解算法如图3所示。

图3 极化目标分解经典算法Fig.3 Classical polarimetric target decomposition algorithms

3.1 相干分解

针对极化后向散射矩阵S的分解算法称为相干分解，表示成几种典型散射机理的加权求和。相干分解对主要散射分量单一的情况比较有效，例如用做定标器的二面角、三面角的散射。此外，相干分解在高分辨率和低熵散射问题中也有一定应用，用于分解相干矩阵T或协方差矩阵C的主要特征矢量。常用的相干分解方法有：Pauli分解、Krogager分解和Cameron分解。Pauli分解比较基础和直观，将散射矩阵S表示为Pauli基矩阵的加权和，即

(7)

式中a，b，c和d为权重系数。每个Pauli基矩阵根据其性质分别与一种基本散射机理相对应：表面散射，方向角为0°和45°的二面角散射，残余分量代表散射矩阵的所有不对称分量。最终求解的权重系数反映每种散射机理所占的比例。Pauli分解虽然效果有限，但是处理简单高效，因此通常作为快速分解算法，初步分析观测区域的散射机理。图4(a)为德国ESAR在Oberpfaffenhofen地区录取的实测数据经过Pauli分解处理的伪彩色合成结果。

Cameron分解仍然基于Pauli基矩阵对散射矩阵进行分解，对于不满足对称性假设的散射体，目的在于提取出目标的最大对称分量。Cameron认为雷达散射目标的两个基本性质是互易性和对称性。当目标严格服从互易定理时，对应的散射矩阵是对称的。Cameron分解将散射矩阵投影到各Pauli基矩阵，根据散射矩阵分解得到的分量生成最大对称分量，使得原散射分量与对称分量之间的残余分量最小化。进一步研究发现，Cameron分解求解最大对称分量的过程，实际是通过目标定向角旋转使同极化通道散射功率最大。因此后文将要介绍的定向角补偿除了使同极化通道散射功率最大，还使得目标旋转到最大对称分量的位置。

除了基于Pauli基的相干分解算法，Krogager分解将散射矩阵表示成圆极化基的形式，保留球对称项，然后提取主要的螺旋散射体分量，残余项就对应极化方向角为θ的二面角散射，因此又称为SDH(球-双平面-螺旋体)分解

(8)

式中:φ表示绝对相位；kS,kD和kH为权重系数。Krogager分解将散射矩阵表示为3个有具体物理意义的相干散射分量之和，建立了3种散射模型与实测数据的直接联系，从而通过3个矩阵分量可以反映实际的电磁散射过程。并且，Krogager分解得到的3个散射分量的权重系数具有旋转不变性。但是Krogager分解后的3个散射分量并不相互正交，因此分解参数不满足基不变特性。图4(b)为Krogager分解处理的伪彩色合成结果。

图4 相干分解处理结果Fig.4 Processing results of coherent decomposition

相干分解的主要缺陷是，对于一个给定的散射矩阵，在缺乏先验信息的情况下，很难确定使用哪种分解方法。另一个问题是，实测数据的散射矩阵通常受到相干斑噪声的影响，相干分解算法在推导过程中没有考虑这一因素。为了更好地解译PolSAR实测数据，通常需要进行相干斑滤波，而相干斑滤波算法大多是基于数据的二阶统计量。因此，研究人员提出了另一类应用更广泛的极化目标分解算法——非相干分解，基于相干矩阵或协方差矩阵这些二阶统计量进行处理。

3.2 非相干分解

3.2.1 基于现象理论的二分量分解

Huynen奠定了非相干分解算法的理论基础，在不利用任何参考模型的条件下，讨论了极化相干矩阵中的参数所包含的实际物理信息。Huynen在文献[52]中提出“现象理论”(Phenomenological theory)，首次明确阐述了目标分解理论，并将其用于雷达目标物理特性和结构信息的提取。对于单一散射目标，Huynen将极化相干矩阵T表示成9个“Huynen参数”的形式

(9)

单一散射目标条件下，T为秩1的Hermitian矩阵，因此可以得到9个参数之间的关系[52]。9个参数对应的物理意义如表1所示。

表1 Huynen参数

对于单一散射目标，可以定义与目标物理特性有关的9个“Huynen”参数。当目标随时间和空间变化时，则需要使用分布式目标的概念。分布式目标的结构有其自身的特点，与静态目标或点目标不同，一般由相干矩阵的统计平均表示。经过平均处理的相干矩阵仍可以表示成9个参数的形式，但参数之间的关系式不再成立，参数间相互独立。由此可见，分布式目标无法由等价的单一散射目标表示。Huynen分解目的在于解决如何将所需目标从杂波环境中区分开的问题，其基本思想是将实测数据的相干矩阵分解成一个平均单一散射目标分量和一个残余分量(称为“N目标”)，因此可以看作是一种二分量分解方法。Huynen分解的基本模型为

T=T0+TN

(10)

式中T0为等价的单一散射目标，TN为“N目标”。图5(a)为Huynen分解处理的伪彩色合成结果。Huynen分解得到的所有目标相互独立，可由参数完全描述且物理可实现。“N目标”用来表示非对称目标参数，由于“N目标”散射特性不随目标旋转角度变化，所以Huynen分解的一个基本性质就是“N目标”具有旋转不变性。Huynen分解虽然利用“N目标”旋转不变性限制了单一散射目标分量的选择，但是并不能提供唯一解。与式(10)中的模型一致，Barnes和Holm在其算法中给出了单一散射目标分量的另外两个解[54]，图5(b)为其中一个解的伪彩色合成结果。杨健等提出的Yang分解[88]通过对Kennaugh矩阵做简单变换，解决了当参数A0相对较小时Huynen分解无法提取预期目标的问题。

图5 二分量分解处理结果Fig.5 Processing results of target dichotomy

非相干分解的另外两类主要方法为：基于特征值特征矢量的分解算法和基于散射模型的分解算法。基于特征值和特征矢量的目标分解具有更加明确的数学理论背景，最终可以得到唯一的分解结果，因此相对更加成熟。与此相反，基于散射模型的目标分解算法能够根据散射模型的变化得到不同的分解结果。

3.2.2 基于特征值和特征矢量的分解算法

由极化相干矩阵和协方差矩阵的定义可以得到，两者均为半正定的Hermitian矩阵，Cloude和Pottier提出直接从半正定Hermitian矩阵的性质出发，通过矩阵分解得到正交的特征矢量和非负实特征值，并证明了这种分解的唯一性，从而提出基于特征值和特征矢量的分解算法。基于特征值和特征矢量的分解算法的数学理论基础是半正定Hermitian矩阵的性质。极化相干矩阵作为Hermitian矩阵，可以利用其特征值和特征矢量表示成一种对角化形式

(11)

(12)

式中：Σ为3个非负实特征值构成的对角矩阵，λ1≥λ2≥λ3≥0；U为归一化特征矢量构成的酉矩阵，每一列对应于相互正交的特征矢量u1，u2和u3。Cloude等提出特征矢量可以由5个角度参数化表示[7,8]

(13)

式中：n=1,2,3；φn表示目标的绝对相位，可以认为是相互独立的；由于特征矢量之间相互正交，因此αn，βn，δn和γn之间不再独立。利用这种对特征矢量参数化表示的方法，可以很方便地对散射机理进行统计方法分析。

与其他分解算法的思路类似，基于特征值和特征矢量的分解算法利用式中相干矩阵的对角化形式，将相干矩阵表示为3个相互独立的目标之和，每个目标对应一种确定的散射机理，与一个等价的简单散射矩阵相关联

(14)

式中:每一种散射机理在整个散射过程中的权重系数由对应的特征值确定，散射机理的类型与归一化特征矢量有关。

Cloude最先展开了这类基于特征值和特征矢量的分解算法的研究[7,8]。Cloude将极化相干矩阵分解为主散射分量和噪声分量，主散射分量对应于最大特征值λ1的特征矢量，得到的矩阵T1确定地物目标中的主要散射机理。Cloude分解对所有的酉变换保持不变，不仅仅是Huynen分解要求的旋转不变。图6(a)为Cloude分解处理的伪彩色合成结果。

Holm对Cloude分解进行了扩展，提出了基于特征值和特征矢量分解算法的另一种物理解释[54]。Holm分解结合了特征值分析、单一散射目标概念和Huynen分解中的噪声模型，将分布式目标理解为一个单一散射目标和两个噪声或残余项之和。该算法对特征值对角阵分解形式为

(15)

结合式(11)和式(15)计算，Holm分解得到的3个散射分量分别对应于：单一散射目标表征了目标的平均形式；混合目标表征了实际目标与其平均形式的差异；噪声项表征了未极化混合状态。式(15)中的组合还能表示成其他形式，Holm分解也随之能获取其他结果。图6(b)为Holm分解处理的伪彩色合成结果。

图6 基于特征值特征矢量的分解处理结果Fig.6 Processing results of eigenvalues-eigenvectors based on decomposition

基于相干矩阵的特征值，研究人员还提取出两个重要的统计性参数。第一个参数是极化散射熵H

(16)

(17)

式中Pn表示散射分量出现的伪概率。容易得到，极化散射熵的数值在0～1之间，表征散射过程的随机性，同时也能反映出依据式(14)能够解译出的有效散射分量的数目。当H=0时，表示平均相干矩阵秩为1，只有1个非零特征值，意味着是单一散射目标；当H=1时，表示存在3个相等的非零特征值，表征为“随机的”或“完全去极化”的目标，且与极化状态完全无关；分布式目标大多介于这两种状态之间的，目标是部分极化的，此时对目标极化特性的分析既需要研究特征值的分布，又需要研究展开式中各种散射机理的表征。

另一个关键参数是极化散射各向异性度A。一般将特征值按照从大到小顺序排列λ1>λ2>λ3>0，各向异性度表示第2个和第3个特征值的差异程度

(18)

A的取值范围也在0～1之间，当A=0时存在两种可能：H=0，表示确定的散射类型；H=1，表示完全随机的散射类型。当极化散射熵的取值介于这两种状态之间时，各向异性度作为极化散射熵的补充，是描述散射特性的有利工具。值得注意的是，极化散射熵H和各向异性度A具有旋转不变性。

(19)

上述3个参数提出至今，研究人员基于特征值和特征矢量的分解算法，开展了大量有意义的工作，如何更稳健地从实测数据中估计这些参数需要进一步研究，同时还根据不同应用需求扩展了其他一些新参数，具体可参见相关文献[63-65, 91-93]。

3.2.3 基于散射模型的分解算法

基于散射模型的极化目标分解是另一类应用广泛的非相干分解方法，其根据一系列实际已知的基本散射模型，对实测数据进行分解，最终将观测区域表示为各种散射模型的组合。根据所选散射模型的不同，基于散射模型的分解算法能够得到不同的分解结果。Freeman-Durden分解(Freeman-Durden decomposition，FDD)是其中一种经典算法，该算法将极化相干矩阵或协方差矩阵表示为3种基本散射分量的组合，分别对应于表面散射、二次散射和体散射。相干矩阵能够更加方便地描述目标的极化散射特性，且与多数文献中的表述一致，因此本文为了便于分析，对传统FDD推导中的协方差矩阵进行替换，使用相干矩阵介绍基于散射模型的分解算法及其改进。

表面散射分量由一阶Bragg表面散射模型表示，模拟微粗糙表面，忽略交叉极化项，极化相干矩阵的表达式为

(20)

(21)

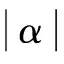
(22)

基于上述3种散射模型，FDD可以表示为

T=fsTs+fdTd+fvTv

(23)

式中:fs，fd和fv分别表示散射分量对应的权重系数。因此，每种散射模型各自的功率可以表示为

(24)

Pv=4fv

图7为FDD处理的伪彩色合成结果。FDD可以用来初步确定每种散射机理在观测区域所占的比重。FDD最初是应用于森林植被的散射特性研究， 实测数据处理

图7 Freeman-Durden分解处理结果Fig.7 Processing result of Freeman-Durden decomposition

表明，FDD在区分混合散射媒质中的散射类型时都能取得一定的效果，例如城市遥感、海洋遥感和地表覆盖等。FDD的优势在于，其利用简单散射模型的组合来匹配复杂的实际散射过程，物理意义更加具体，而不仅仅是单纯的数学计算。FDD虽然物理意义简单明了，实现也比较容易，但是由于观测区域的复杂性，传统FDD中的散射模型或者前提假设与实际散射特性不相符，严重影响到最终的分解效果。例如算法基于反射对称性假设，令同极化分量与交叉极化分量的相关系数为零，简化了散射模型的构造和权重系数的估计，实测数据通常难以满足该假设条件。研究人员对FDD进行了深入研究，以提高散射机理的解译精度，拓展基于散射模型的分解算法的适用范围。

4 基于散射模型分解算法的改进

传统FDD虽然物理意义比较明确，但是如果使用的模型或者前提假设与观测区域的地物特性不相符，最终的分解效果将不够理想。基于散射模型的分解算法的研究主要针对以下4个方面：(a)反射对称性假设，这是FDD的重要前提，同极化分量与交叉极化分量的相关系数为零，简化散射模型的构造，但是对大多数人造目标不再适用；(b)定向角(又称为极化方向角)效应，当散射目标的定向角较大时，会产生不可忽略的交叉极化功率分量，尤其是人造目标，造成最终分解结果中体散射分量过估计，如图7所示，图像整体偏绿；(c)FDD不能完全与实际地物的散射特性相匹配，在计算过程中造成表面散射分量和二次散射分量的功率值为负值；(d)散射模型的构造和选取，使得与观测区域的极化数据更加匹配。研究人员进行了大量的深入研究，提出了很多有意义的改进，下面从这4个方面来介绍一些代表性的方法。

4.1 反射对称性假设的影响

为了使算法匹配反射对称性假设不成立的情况，Yamaguchi等[56]在三分量散射模型的基础上提出了四分量散射模型。第4个散射模型的极化相干矩阵表达式为

(25)

该模型等价于螺旋散射体，引入了同极化分量与交叉极化分量的相关系数不为零的附加项，以表征反射对称性假设不成立的情况。螺旋散射体通常存在于具有复杂结构的目标或人造建筑，在分布式自然散射介质中几乎不存在。图8为Yamaguchi分解处理的伪彩色合成结果，与图7对比，可以看出效果明显改善。

4.2 定向角补偿

同一目标的极化响应会随定向角的变化而改变，目标散射类型的区分容易受到定向角的影响，从而产生误差。尤其是定向角较大的人造目标，会产生不可忽略的交叉极化功率分量，对分解结果影响更大。定向角补偿，又称为去定向角(Deorientation)，通过极化矩阵围绕雷达视线方向旋转一定角度，使得交叉极化功率分量最小，从而降低定向角的影响[94-96]。

图8 Yamaguchi分解处理结果Fig.8 Processing result of Yamaguchi decomposition

实际观测情况中，地形存在起伏，建筑物等人造目标也并不总是垂直于雷达视线，定向角与地形坡度和雷达视角之间存在一个散射几何关系[59]。定向角会引入显著的交叉极化功率分量。然而，如前文所介绍的，传统的FDD在估计表面散射和二次散射的功率分量时，使用的散射模型中交叉极化项均为零。FDD在处理时默认实测数据中的交叉极化功率分量全部来自于体散射目标，因此造成最终分解结果中的体散射功率分量过估计。尤其是存在定向角的建筑物和山坡，通常会被误判为体散射目标，严重降低极化目标分解的精度。

补偿的前提是对定向角进行准确的估计，圆极化算法是其中比较有效的算法，应用十分广泛。圆极化算法的具体推导过程可以参考文献[59,60,97]，这里给出最终的结论

图9 结合定向角补偿的FDD处理结果 Fig.9 Processing result of FDD with deorientation

(26)

式中ReT23表示T23的实部。利用估计的定向角构造相应的旋转矩阵，绕视线方向旋转极化矩阵，即可完成定向角补偿。图9为结合定向角补偿的FDD处理的伪彩色合成结果，散射模型仍然与传统算法一致。

通过定向角补偿处理，T33的数值降低到最小，同时T22提高相同的数值[94]。这也是文献[95,98]中估计定向角的基本思想，即通过定向角补偿使得同极化功率分量达到最大，等价于使交叉极化功率分量达到最小，得到的估计结果与式(26)一致。由式(4)可知，T33对应于交叉极化功率分量，决定了最终的体散射功率分量估计结果。定向角补偿后，体散射功率分量随之降低，二次散射功率分量提高，表面散射功率分量几乎不变，螺旋散射体由于具有旋转不变性，不受定向角的影响。因此，定向角补偿能够一定程度上解决体散射功率分量过估计的问题。同时，T22的增大对负功率值的问题也有明显的改善[94,95]，因为造成表面散射或二次散射功率值为负的一个主要原因就是T22

然而，定向角补偿并不是在所有情况下都能取得良好的效果。对于定向角位于雷达视线垂直平面的目标，定向角的影响能够被完全去除；对于定向角位于其他平面的目标，定向角补偿的效果就会大打折扣[97,98]。文献[98,99]证明，尤其当定向角为45°时，定向角补偿几乎完全失效。因此，对于某些建筑物目标，即使经过定向角补偿，仍然具有较大的交叉极化功率分量。一类有效的方法是扩展体散射模型，通过考虑定向角的影响，构造自适应的体散射模型[99,100]，与地物特性更好地匹配，后文将详细介绍这类方法。如何对人造目标和地形坡度进行完全的定向角补偿，仍是值得深入研究的方向。

定向角还能够用于改进散射模型。对于定向角为零的建筑物来说，其产生的二次散射较强，能够用式的二面角反射器模型来表征；对于定向角不为零的建筑物来说，则产生不能忽略的交叉极化功率分量，使得整个实测数据的交叉极化功率分量增大。传统FDD认为交叉极化分量全部来自体散射，造成存在定向角的建筑物区域体散射分量过估计。研究人员指出，对于存在定向角的建筑区域，其产生的交叉极化分量既不符合体散射模型，又不符合二次散射模型[101]。文献[101]提出了一种交叉散射模型来匹配存在定向角的建筑物区域，结合定向角来构造极化矩阵

(27)

式中θ为定向角的估计值。该方法将建筑物目标产生的交叉极化分量从整个极化数据中单独提取出来，构造了一种新的散射模型，从而提高了目标的识别能力。

通过前文的介绍，可以知道定向角补偿的本质是对极化矩阵进行旋转，使得交叉极化分量最小；如果将极化矩阵旋转其他角度，可能会对矩阵中的各元素造成影响呢。基于这个思路，文献[102]进行延伸研究，提出了极化矩阵一致旋转理论。相关文献指出，极化相干矩阵旋转一定角度后，矩阵元素都能以正弦函数形式统一表示，正弦函数的幅度、频率和初相可以用来描述散射特性随旋转角度的变化。文中推导了一系列角度，以此来使旋转后的极化矩阵满足某一特定性质。上述推导的参量都具有特定的物理含义，与Huynen参数有直接联系。因此，一致旋转技术能够通过极化矩阵旋转特定的角度，使得某一Huynen参数达到期望值。经过实测数据的验证，一致旋转技术在人造目标识别和非监督分类应用中取得了不错的效果[102]，其他应用需要未来继续研究。

4.3 负功率值问题

传统FDD首先求得体散射模型的权重系数fv=T33，极化相干矩阵减去体散射模型对应的相干矩阵分量

(28)

由式(28)易得，要使得表面散射和二次散射分量的功率非负，需要满足以下条件

(29)

式中:第1个不等式与表面散射的功率有关，第2个不等式与二次散射的功率有关。第2个不等式也验证了定向角补偿对负功率值问题的改善。

图10 NNED处理结果 Fig.10 Processing result of NNED

除了定向角补偿可以减少负功率值的像素数量，研究人员还提出了其他有效的方法。第1类方法是将基于散射模型的分解算法与基于特征值的分解算法相结合，利用特征值分解的特性来改善负功率值问题。Cloude提出了一种广义FDD[8]，该算法仍然使用传统FDD中的体散射模型，对表面散射和二次散射的功率估计则采用特征值的方法，因此该算法称为Freeman-Durden/特征值混合分解算法。该方法假设表面散射与二次散射正交，这样可以用一种散射机理来表示另一种，从而可以减少待估计的模型未知参数，得到5个参数和5个观测量的平衡系统。该方法有效避免了负功率值的出现，还可以估计表面散射和体散射分量的比值，称为地体幅度比，是极化干涉测量中的一个重要参数[8]。另外一种方法是由van Zyl等提出的非负特征值分解(Nonnegative eigenvalue decomposition，NNED)[103]，该方法从理论基础上解决负功率值的问题。图10为NNED处理的伪彩色合成结果。NNED基于反射对称性假设，引入非负特征值约束准则(Nonnegative eigenvalue constraint，NNEC)，令式(28)中减去体散射分量后的残余相干矩阵Tremainder的特征值非负，计算满足条件的体散射分量功率最大值，文献[103]给出了体散射分量功率最大值的解析表达式。NNED中只需要使用体散射模型估计体散射分量的功率，表面散射和二次散射分量的功率则是通过特征值和特征矢量来估计。为了消除反射对称性假设的影响，研究人员提出了NNED的后续改进算法。Kusano等对极化相干矩阵的主子式进行分析[104]，将体散射分量功率的约束条件推广到非反射对称性情况中。文献[105]对NNEC进行了推广，在某些特定条件下，体散射分量功率的最大值可以不需要基于反射对称性假设得到。

第2类方法是对散射模型进行改进，不再基于反射对称性假设，通过改变传统散射模型中的参数，采用自适应的散射模型，该方法又称为广义散射模型分解算法。文献[106,107]中提出了广义散射模型分解的处理框架，通过线性或者非线性优化算法来估计模型中的未知参数。广义散射模型分解的表达形式为

T=fvTv+fdTd+fsTs+fhTh+…+frTresidual

(30)

式中：Tresidual可以看作是相干斑、噪声、与模型不匹配的目标等对极化数据的贡献。式(30)如何选取适当的散射模型，所依据的准则是能确保参数估计成为确定性问题。Tresidual为衡量这些散射模型与观测目标匹配程度的物理量。因此，对于参数估计、模型反演等问题，优化准则即为Tresidual最小。文献[106，107]中是令Tresidual的二范数最小，即

(31)

式(31)能够通过非线性的最小二乘法进行求解，获得参数的最优估计，还可以避免反射对称性假设和负功率值问题。需要注意的是，通过广义散射模型分解算法并不能使选取的散射模型与观测区域精确匹配，而是在一定准则下使所有像素单元均能求得非负功率值的最优解。非线性优化通常需要大量的处理时间，得到的也只是局部最优解，仍有需要进一步研究的地方。

4.4 散射模型的改进

前文已经介绍了基于散射模型分解算法实际处理中遇到的3个问题，以及相应的改进方法。进一步研究发现，这些改进算法总会不可避免地存在一些局限性。传统FDD预先定义了3种散射模型的极化矩阵，简洁直观，易于处理，但也缺乏自适应性。因此，无论反射对称性限制，还是定向角效应和负功率值问题，其本质都可以归结为选取的散射模型与实际观测数据不匹配。前文所述方法的思路是对极化相干矩阵或协方差矩阵进行预处理，以使得观测数据能够与传统散射模型更加吻合，提高FDD的性能。另一方面，还可以从改进散射模型的角度来改善最终的分解效果。根据不同的应用需求，研究人员从多种角度对散射模型进行了修正。表面散射和二次散射模型的改进主要是针对传统模型中忽略交叉极化项的不足，对于方位向地形坡度和存在定向角的建筑物，交叉极化项的影响尤为显著。基于一种截断的均匀概率密度分布，X-Bragg模型[8]扩展了原始Bragg模型，引入了交叉极化项，表征表面散射的去极化效应。文献[108]推导了表面散射和二次散射模型的广义形式。文献[107]则通过分离表面散射和二次散射相互独立的极化方向角，匹配交叉极化项和极化矩阵中的非对角线项，构造了另一种广义散射模型。在散射模型研究中，以体散射模型最为广泛深入，下面具体介绍几种改进的体散射模型。

传统FDD在构造体散射模型时，假设偶极子的极化方向角满足均匀概率密度分布。为了更符合实际目标的散射特性，研究人员引入了其他概率密度分布。Yamaguchi算法根据植被覆盖区域的复杂结构，提出了一种半余弦概率密度分布[56]

(32)

式中，θ是偶极子与水平方向的极化方向角。改进后的体散射模型具有非对称形式

(33)

此外，经验性体散射模型是另一种广泛应用的改进措施。Freeman提出了一种二分量散射模型[110]，引入一个形态参数变量，将森林冠层近似成一片由随机取向的类圆柱体构成的云层

(34)

式中ρ为形态参数变量，由水平和垂直两个同极化通道功率比值定义。安文韬在文献[95]中提出了另一种改进的体散射模型。文献指出，相比于表面散射和二次散射，体散射的主要特点是结构比较复杂，由多种散射机理构成，表现出一种混乱的散射状态，极化相干矩阵的随机性也较高。Cloude等提出的极化散射熵概念，可以衡量相干矩阵的随机性。研究人员对大量实际观测数据进行分析得到，对于大量植被覆盖的区域，体散射目标比较多，极化散射熵较高。因此，文献[95]利用极化散射熵为1定义了改进的体散射模型，表征完全随机的散射目标

(35)

对比式(34)与式(35)可以发现，式(35)是式(34)在ρ=0时的特例。该模型的主要优点在于其完全随机性，而这也是体散射目标的最主要特性；此外，该体散射模型还能有效减少负功率值的像素数目。图11为该分解算法的伪彩色合成结果，使用式(35)中的体散射模型，并结合定向角补偿，称为An分解。

图11 An分解处理结果 Fig.11 Processing result of An decomposition

上述改进模型有一个共同特点，体散射模型的自适应不强，即使Yamaguchi算法能够根据门限在3个体散射模型之间选择，仍然不具备较好的自适应性。陈思伟等提出了一种自适应的体散射模型[100]，相干矩阵中的有关参数随像素单元的散射特性而变化，能更好地与实测数据匹配。传统表面散射和二次散射模型中假设交叉极化项为零，因此，分解算法认为这两类散射对极化数据中的交叉极化项T33没有贡献，估计过程中认为交叉极化功率完全来自体散射分量。文献指出，式(33,35)中使用的体散射模型参数都是固定常数，因此，最终体散射分量的功率完全由T33和模型参数决定。文献[100]对已有的体散射模型进行分析，推导了与之相匹配的体散射分量功率动态范围

(36)

前文已经分析，存在定向角的人造目标也会引入不可忽略的交叉极化功率。因此，自适应的体散射模型应该能够符合更一般的情况，与更多的散射目标相匹配。体散射分量功率动态范围也需要扩展为

(37)

要精确地识别每种散射类型的目标并不是很简单，但是，人们期望至少不会将人造目标与非人造目标混淆。文献[100]基于这个目的，提出了一种有效的自适应体散射模型，体散射分量功率的动态范围满足式(37)。该模型基于极化干涉SAR(PolInSAR)在森林观测领域的先天优势，根据干涉复相干性与森林结构目标的紧密关系，将体散射模型中的参数以干涉相关系数来表示。通常，在干涉测量中，由于散射特性的不同，人造目标表现为高相干性，非人造目标(如森林植被)则表现为低相干性。干涉复相干性的计算根据不同条件会得到不同的结果，具体的自适应体散射模型需要根据这些不同的干涉相关系数来构造。详细证明和应用过程可以参考文献[99，100]。对ESAR在Oberpfaffenhofen地区以干涉模式录取的实测数据进行处理，图12(a)使用的是传统FDD，图12(b)使用的是文献[100]中的Chen分解，对比人造目标的分解效果可以看出，基于干涉复相干性构造的自适应体散射模型能够改善算法性能。

图12 PolInSAR目标分解处理结果Fig.12 Processing results of PolInSAR target decomposition

通过上述介绍，可以发现，不同改进方法之间并不是独立，而是存在一种相互影响的关系。针对某一个问题的改进方法，可能对另一个问题也有改善，同时也可能使其他问题更加复杂。但是这些改进方法都有同一个核心，那就是使得基于散射模型的分解算法与实际目标的散射特性更加匹配。

5 实测数据处理试验

基于某型号机载合成孔径雷达的外场实测数据进行了试验。雷达全极化双通道成像，作用距离25 km，分辨率0.5 m×0.5 m(斜距×方位)。图13为水平同极化通道回波数据的成像处理结果，其中图13(a)为提取的相位误差曲线；图13(b)为Omega-K算法直接成像得到的局部图像，未进行运动补偿；图13(c)为结合运动补偿的Omega-K算法成像得到的局部图像，处理流程如图1所示。图13(b，c)对比可以看出，需要对运动误差进行精确补偿，才能获取聚焦良好的图像，以确保后续极化处理的精度。

图14为全极化数据目标分解处理结果。图13(c)和图14(a～c)对比可以看出，经过极化目标分解处理，不同散射类型目标之间的差异更加明显，相对于传统单极化SAR来说，图像解译能力得到增强。图14(c)给出了Freeman-Durden分解的缺陷，传统算法由于散射模型与实测数据不匹配，造成分解效果不够理想，最直观的表现就是体散射功率分量过估计(图像整体偏绿)，仍然需要对改进方法进行研究，提高算法性能。

图13 水平同极化通道处理结果Fig.13 Processing results of horizontal co-polarization channel

图14 极化目标分解处理结果Fig.14 Processing results of polarimetric target decomposition

6 结束语

极化合成孔径雷达作为一种迅速发展的技术，结合了高分辨率雷达成像和极化信息处理，受到了广泛的关注，在大量机载、星载雷达系统中得到了应用。散射机理解译是PolSAR应用的重要前提，因此极化目标分解算法一直是研究的重点。本文首先介绍了PolSAR的主要应用研究进展，对极化目标分解算法的理论基础进行了阐述。基于散射模型的非相干分解算法与目标散射特性联系更加紧密，物理意义更加明确，因此受到广泛的关注。本文对其中的关键问题进行了分析，并介绍了相应的改进方法。同时，结合实测数据处理结果，进一步验证了PolSAR在散射机理解译方面的优势。目前极化目标分解算法的研究应侧重于以下几个方面：(1)超高分辨率条件下极化目标分解算法的改进，主要针对散射模型的构造和极化矩阵的自适应估计；(2)人造目标和自然目标的识别区分，获取更多有效的极化散射特征参量，提高参量估计的精度；(3)极化矩阵信息的完全利用，每个矩阵元素都有其物理含义，目前的算法大多只使用部分元素，极化信息并没有充分利用；(4)极化目标分解算法性能的评价标准，目前的评价指标并不完善，需要制定更多可行的评价参数。极化合成孔径雷达正处于发展的黄金时代，其作为基础理论与实验科学紧密结合并相互促进的典型研究领域之一，涉及多个学科，必定带来更多的发展机遇。

[1] Reigber A, Scheiber R, Jager M, et al. Very high resolution airborne synthetic aperture radar imaging: Signal processing and applications[J]. Proceedings of the IEEE, 2012, 101(3): 759-783.

[2] Moreira A, Prats-Iraola P, Younis M, et al. A tutorial on synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Magazine, 2013, 1(1): 6-43.

[3] Carrara W G, Goodman R S, Majewski R M. Spotlight synthetic aperture radar signal processing algorithms[M]. Boston: Artech House, 1995.

[4] Cumming I G, Wong F H. Digital processing of synthetic aperture radar data: Algorithms and implementation[M]. Boston: Artech House, 2005.

[5] 朱岱寅, 俞翔, 汪玲. 海面舰船目标ISAR最优成像时间选择算法[J]. 数据采集与处理, 2014, 29(4): 526-532.

Zhu Daiyin, Yu Xiang, Wang Ling. Optimal processing time and duration selection algorithm for ISAR[J]. Journal of Data Acquisition and Processing, 2014, 29(4): 526-532.

[6] 宋伟, 朱岱寅, 李勇. 机载聚束SAR图像定位精度研究[J]. 数据采集与处理, 2014, 29(4): 555-561.

Song Wei, Zhu Daiyin, Li Yong. Airborne spotlight SAR geolocation accuracy[J]. Journal of Data Acquisition and Processing, 2014, 29(4): 555-561.

[7] Lee J S, Pottier E. Polarimetric radar imaging: From basics to applications[M]. Boca Raton, FL: CRC Press, 2009.

[8] Cloude S R. Polarisation application in remote sensing[M]. New York: Oxford University Press, 2010.

[9] Chen S W, Li Y Z, Wang X S, et al. Modeling and interpretation of scattering mechanisms in polarimetric synthetic aperture radar: Advances and perspectives[J]. Signal Processing Magazine IEEE, 2014, 31(4): 79-89.

[10]Ahmed A R, Strom H, Bierman S, et al. Polarimetric backscattering coefficients of flooded rice fields at L- and C-bands: Measurements, modeling and data analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(8): 2714-2721.

[11]Yin J J, Zhou Z S, Moon W M, et al. The use of a modified GOPCE method for forest and nonforest discrimination[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(5): 1076-1080.

[12]Yeremy M, Campbell J W M, Mattar K, et al. Ocean surveillance with polarimetric SAR[J]. Canadian Journal of Remote Sensing, 2014, 27(4): 328-344.

[13]He L, Panciera R, Tanase M A, et al. Soil moisture retrieval in agricultural fields using adaptive model-based polarimetric decomposition of SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(8): 4445-4460.

[14]Li X W, Guo H D, Zhang L, et al. A new approach to collapsed building extraction using RADARSAT-2 polarimetric SAR imagery[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4): 677-681.

[15]Raney R K, Runge H, Bamler R, et al. Precision SAR processing using chirp scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(4): 786-799.

[16]Moreira A, Mittermayer J, Scheiber R. Extended chirp scaling algorithm for air- and spaceborne SAR data processing in stripmap and scan SAR imaging modes[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(5): 1123-1136.

[17]Amein A S, Soraghan J J. Azimuth fractional transformation of the fractional chirp scaling algorithm (FrCSA)[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(10): 2871-2879.

[18]Davidson G W, Cumming I G, Ito M R. A chirp scaling approach for processing squint mode SAR data[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(1): 121-133.

[19]Mittermayer J, Moreira A, Loffeld O. Spotlight SAR data processing using the frequency scaling algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2198-2214.

[20]Cafforio C, Prati C, Rocca F. SAR data focusing using seismic migration techniques[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(2): 194-207.

[21]Reigber A, Alivizatos E, Potsis A, et al. Extended wavenumber-domain synthetic aperture radar focusing with integrated motion compensation[J] IEE Proceedings - Radar Sonar and Navigation, 2006, 153(3): 301-310.

[22]Zhu D Y, Ye S H, Zhu Z D. Polar format algorithm using chirp scaling for spotlight SAR image formation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(4): 1433-1448.

[23]Desai M D, Jenkins W K. Convolution backprojection image reconstruction for spotlight mode synthetic aperture radar[J]. IEEE Transactions on Image Processing, 1992, 1(4): 505-517.

[24]Buckreuss S. Motion Compensation for airborne SAR based on inertial data, RDM and GPS[C]∥ Geoscience and Remote Sensing Symposium. IGARSS ′94. Surface and Atmospheric Remote Sensing: Technologies, Data Analysis and Interpretation. Pasadena, USA: IEEE, 1994: 1971-1973.

[25]Calloway T M, Donohoe G W. Subaperture autofocus for synthetic aperture radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(2): 617-621.

[26]Snarski C A. Rank one phase error estimation for range-doppler imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(2): 676-688.

[27]Wahl D E, Eichel P H, Ghiglia D C, et al. Phase gradient autofocus—A robust tool for high resolution SAR phase correction[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(3): 827-835.

[28]Zhu D Y, Jiang R, Mao X H, et al. Multi-subaperture PGA for SAR autofocusing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 468-488.

[29]Sinclair G. The transmission and reception of elliptically polarized waves[J]. Proceedings of the Ire, 1950, 38(2): 148-151.

[30]Kostinski A, Boerner W M. On the polarimetric contrast optimization[J]. IEEE Transactions on Antennas and Propagation, 1987, 35(8): 988-991.

[31]Ioannidis G, Hammers D. Optimum antenna polarizations for target discrimination in clutter[J]. IEEE Transactions on Antennas and Propagation, 1979, 27(3): 357-363.

[32]Yang J, Yamaguchi Y, Boerner W M, et al. Numerical methods for solving the optimal problem of contrast enhancement[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(2): 965-971.

[33]Yang J, Peng Y N, Lin S M. Similarity between two scattering matrices[J]. Electronics Letters, 2001, 37(3): 193-194.

[34]Yang J, Dong G W, Peng Y N, et al. Generalized polarimetric contrast enhancement[J]. IEEE Geoscience Remote Sensing Letters, 2004, 1(3): 171-174.

[35]王雪松. 宽带极化信息处理的研究[D]. 长沙: 国防科学技术大学, 1999.

Wang Xuesong. Study of wide-band polarization information processing[D]. Changsha, China: National University of Defense Technology, 1999.

[36]徐牧. 极化SAR图像人造目标提取与几何结构反演研究[D]. 长沙: 国防科学技术大学, 2008.

Xu Mu. Extraction and geometrical structure retrieval of man-made target in PolSAR imagery[D]. Changsha, China: National University of Defense Technology, 2008.

[37]代大海. 极化雷达成像及目标特征提取研究[D]. 长沙: 国防科学技术大学, 2008.

Dai Dahai. Study on polarimetric radar imaging and target feature extraction[D]. Changsha, China: National University of Defense Technology, 2008.

[38]Ulaby F T, Sarabandi K, Nashashibi A. Statistical properties of the Mueller matrix of distributed targets[J]. Radar and Signal Processing IEE Proceedings F, 1992, 139(2): 136-146.

[39]Lee J S, Schuler D L, Lang R H, et al. K-distribution for multi-look processed polarimetric SAR imagery[C]∥ Geoscience and Remote Sensing Symposium, IGARSS′94. Surface and Atmospheric Remote Sensing: Technologies, Data Analysis and Interpretation International. Pasadena, USA:IEEE,1994: 2179-2181.

[40]Lee J S, Grunes M R, Kwok R. Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution[J]. International Journal of Remote Sensing, 1994, 15(15): 2299-2311.

[41]Lee J S, Grunes M R, Mango S A. Speckle reduction in multipolarization, multifrequency SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 1991, 29(4): 535-544.

[42]Lee J S, Grunes M R, De Grandi G. Polarimetric SAR speckle filtering and its implication for classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2363-2373.

[43]Lee J S, Jurkevich L, Dewaele P, et al. Speckle filtering of synthetic aperture radar images: A review[J]. Remote Sensing Reviews, 1994, 8(4): 255-267.

[44]Lee J S, Ainsworth T L, Wang Y, et al. Polarimetric SAR speckle filtering and the extended Sigma filter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1150-1160.

[45]Foucher S, Lopezmartinez C. Analysis, evaluation, and comparison of polarimetric SAR speckle filtering techniques[J]. IEEE Transactions on Image Processing, 2014, 23(4): 1751-1764.

[46]Touzi R. A review of speckle filtering in the context of estimation theory[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2392-2404.

[47]Goze S, Lopes A. A MMSE speckle filter for full resolution SAR polarimetric data[J]. Journal of Electromagnetic Waves and Applications, 1993, 7(7): 717-737.

[48]Novak L M, Burl M C. Optimal speckle reduction in polarimetric SAR imagery[J]. IEEE Transactions on Aerospace and Electronic Systems, 1990, 26(2): 293-305.

[49]Lopes A, Sery F. Optimal speckle reduction for the product model in multilook polarimetric SAR imagery and the Wishart distribution[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(3): 632-647.

[50]Krogager E. New decomposition of the radar target scattering matrix[J]. Electronics Letters, 1990, 26(18): 1525-1527.

[51]Cameron W L, Youssef N N, Leung L K. Simulated polarimetric signatures of primitive geometrical shapes[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(3): 793-803.

[52]Huynen J R. Phenomenological theory of radar targets[D]. Delft: Delft University, 1970.

[53]Cloude S R, Pottier E. A review of target decomposition theorems in radar polarimetry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(2): 498-518.

[54]Holm W A, Barnes R M. On radar polarization mixed target state decomposition techniques[C]∥ Radar Conference, Proceedings of the 1988 IEEE National. Ann Arbor, USA: IEEE, 1988: 249-254.

[55]Freeman A, Durden S L. A three-component scattering model for polarimetric SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 963-973.

[56]Yamaguchi Y, Moriyama T, Ishido M, et al. Four-component scattering model for polarimetric SAR image decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(8): 1699-1706.

[57]Cloude S R, Pottier E. Concept of polarization entropy in optical scattering[J]. Optical Engineering, 1995, 34(34): 1599-1610.

[58]Cloude S R, Pottier E. An entropy based classification scheme for land applications of polarimetric SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1): 68-78.

[59]Lee J S, Schuler D L, Ainsworth T L. Polarimetric SAR data compensation for terrain azimuth slope variation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2153-2163.

[60]Lee J S, Schuler D L, Ainsworth T L, et al. On the estimation of radar polarization orientation shifts induced by terrain slopes[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(1): 30-41.

[61]Pottier E, Boerner W M, Schuler D L. Polarimetric detection and estimation of ship wakes[C]∥ Geoscience and Remote Sensing Symposium, IGARSS ′99 Proceedings. Hamburg, Germany: IEEE, 1999: 2458-2460.

[62]Hajnsek I, Pottier E, Cloude S R. Inversion of surface parameters from polarimetric SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(4): 727-744.

[63]van Zyl J J. Application of Cloude′s target decomposition theorem to polarimetric imaging radar data[J]. Proceedings of SPIE—The International Society for Optical Engineering, 1993, 1748: 184-191.

[64]Durden S L, van Zyl J J, Zebker H A. The unpolarized component in polarimetric radar observations of forested areas[J]. IEEE Transactions on Geosciences and Remote Sensing, 1990, 28(2): 268-271.

[65]van Zyl J J, Zebker H A, Elachi C. Imaging radar polarization signatures: Theory and observation[J]. Radio Science, 1987, 22(4): 529-543.

[66]Kong J A, Swartz A A, Yueh H A, et al. Identification of terrain cover using the optimum polarimetric classifier[J]. Journal of Electromagnetic Waves and Applications, 1988, 2(2): 171-194.

[67]van Zyl J J, Burnette C F. Bayesian classification of polarimetric SAR images using adaptive a priori probabilities[J]. International Journal of Remote Sensing, 1992, 13(5): 835-840.

[68]Lee J S, Grunes M R, Ainsworth T L, et al. Unsupervised classification using polarimetric decomposition and the complex Wishart classifier[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2249-2258.

[69]Ferro-Famil L, Pottier E, Lee J S. Unsupervised classification and analysis of natural scenes from polarimetric interferometric SAR data[C]∥ Geoscience and Remote Sensing Symposium, IGARSS ′01. Sydney, Australia: IEEE, 2001: 2715-2717.

[70]Ferro-Famil L, Pottier E, Lee J S. Unsupervised classification of multifrequency and fully polarimetric SAR images based onH/A/Alpha Wishart classifier[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(11): 2332-2342.

[71]Lee J S, Grunes M R, Pottier E, et al. Unsupervised terrain classification preserving polarimetric scattering characteristics[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(4): 722-731.

[72]Du L J, Lee J S. Fuzzy classification of earth terrain covers using complex polarimetric SAR data[J]. International Journal of Remote Sensing, 1996, 17(17): 809-826.

[73]Chen K S, Huang W P, Tsay D H, et al. Classification of multifrequency polarimetric SAR imagery using a dynamic learning neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(3): 814-820.

[74]Tzeng Y C, Chen K S. A fuzzy neural network to SAR image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(1): 301-307.

[75]Antropov O, Rauste Y, Astola H, et al. Land cover and soil type mapping from spaceborne PolSAR data at L-band with probabilistic neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013(9):1-15.

[76]Du L J, Lee J S, Hoppel K, et al. Segmentation of SAR images using the wavelet transform[J]. International Journal of Imaging Systems and Technology, 1992, 4(4): 319-326.

[77]De Grandi G D, Lee J S, Schuler D L. Target detection and texture segmentation in polarimetric SAR images using a wavelet frame: Theoretical aspects[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3437-3453.

[78]Chaney R D, Bud M C, Novak L M. On the performance of polarimetric target detection algorithms[J]. IEEE Aerospace and Electronic Systems Magazine, 1990, 5(11): 10-15.

[79]Novak L M, Sechtin M B, Cardullo M J. Studies of target detection algorithms that use polarimetric radar data[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(2): 150-165.

[80]Novak L M, Burl M C, Irving W W. Optimal polarimetric processing for enhanced target detection[J]. IEEE Transactions on Aerospace Electronic Systems, 1993, 29(1): 234-244.

[81]Novak L M, Hesse S R. Optimal polarizations for radar detection and recognition of targets in clutter[J]. Proceedings of SPIE—The International Society for Optical Engineering, 1993, 1700: 79-83.

[82]Ainsworth T L, Schuler D L, Lee J S. Polarimetric SAR characterization of man-made structures in urban areas using normalized circular-pol correlation coefficients[J]. Remote Sensing of Environment, 2008, 112(6):2876-2885.

[83]Chen S W, Li Y Z, Wang X S, et al. Manmade target extraction in PolSAR data using polarimetric coherence optimization[C]∥ IET International Radar Conference 2015. Hangzhou, China: IET, 2015: 1-4.

[84]Jeon B K, Jang J H, Hong K S. Road detection in spaceborne SAR images using a genetic algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(1): 22-29.

[85]Cameron W L, Youssef N N, Leung L K. Simulated polarimetric signatures of primitive geometrical shapes[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(3): 793-803.

[86]Touzi R, Raney R K, Charbonneau F. On the use of permanent symmetric scatters for ship characterization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(10): 2039-2045.

[87]Howell C, Power D, Lynch M, et al. Dual polarization detection of ships and icebergs-recent results with ENVISAT ASAR and data simulations of RADARSAT-2[C]∥ IGARSS 2008,2008 IEEE International Geoscience and Remote Sensing Symposium. Boston, USA: IEEE, 2008: III-206-209.

[88]Yang J, Peng Y N, Yamaguchi Y, et al. On Huynen′s decomposition of a Kennaugh matrix[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(3): 369-372.

[89]Dabboor M, Collins M J, Karathanassi V, et al. An unsupervised classification approach for polarimetric SAR data based on the Chernoff distance for complex Wishart distribution[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(7): 4200-4213.

[90]Cheng X G, Huang W L, Gong J Y. An unsupervised scattering mechanism classification method for PolSAR images[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(10): 1677-1681.

[91]Allain S, Ferro-Famil L, Pottier E. Two novel surface model based inversion algorithms using multi-frequency polSAR data[C]∥ Geoscience and Remote Sensing Symposium, IGARSS ′04. Anchorage, USA: IEEE, 2004: 823-826.

[92]Réfrégier P, Morio J. Shannon entropy of partially polarized and partially coherent light with Gaussian fluctuations[J]. Journal of the Optical Society of America： A Optics Image Science and Vision, 2006, 23(12): 3036-44.

[93]Ainsworth T L, Cloude S R, Lee J S. Eigenvector analysis of polarimetric SAR data[C]∥ Geoscience and Remote Sensing Symposium, IGARSS ′02. [S.l.]:IEEE, 2002，1: 626-628.

[94]Lee J S, Ainsworth T L. The effect of orientation angle compensation on coherency matrix and polarimetric target decompositions[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 53-64.

[95]An W T, Cui Y, Yang J. Three-component model-based decomposition for polarimetric SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(6): 2732-2739.

[96]Yamaguchi Y, Sato A, Boerner W M, et al. Four-component scattering power decomposition with rotation of coherency matrix[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2251-2258.

[97]Xu F, Jin Y Q. Deorientation theory of polarimetric scattering targets and application to terrain surface classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(10): 2351-2364.

[98]Chen S W, Ohki M, Shimada M, et al. Deorientation effect investigation for model-based decomposition over oriented built-up areas[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(2): 273-277.

[99]Du A, Wang Y. Compensation for azimuth angle or scale effect on building extraction in urban using SAR scales of polarization and coherence[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016(99): 1-9.

[100]Chen S W, Wang X S, Li Y Z, et al. Adaptive model-based polarimetric decomposition using PolInSAR coherence[J]. IEEE Transactions on Geoscience & Remote Sensing, 2014, 52(3): 1705-1718.

[101]Xiang D L, Ban Y F, Su Y. Model-based decomposition with cross scattering for polarimetric SAR urban areas[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(12): 2496-2500.

[102]Chen S W, Wang X S, Sato M. Uniform polarimetric matrix rotation theory and its applications[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(8): 4756-4770.

[103]van Zyl J J, Arii M, Kim Y. Model-based decomposition of polarimetric SAR covariance matrices constrained for nonnegative eigenvalues[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3452-3459.

[104]Kusano S, Takahashi K, Sato M. Volume scattering power constraint based on the principal minors of the coherency matrix[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(1): 361-365.

[105]Cui Y, Yamaguchi Y, Yang J, et al. On complete model-based decomposition of polarimetric SAR coherency matrix data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(4): 1991-2001.

[106]Arii M, van Zyl J J, Kim Y. Adaptive model-based decomposition of polarimetric SAR covariance matrices[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(3): 1104-1113.

[107]Chen S W, Sato M. General polarimetric model-based decomposition for coherency matrix[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(3): 1843-1855.

[108]Lee J S, Ainsworth T L, Wang Y T. Generalized polarimetric model-based decompositions using incoherent scattering models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5): 2474-2491.

[109]Neumann M, Ferro-Famil L, Reigber A. Improvment of vegetation parameter retrieval from polarimetric SAR interferometry using a simple polarimetric scattering model[C]∥Processing POLinSAR. Rome, Italy: [s.n.],2009.

[110]Freeman A. Fitting a two-component scattering model to polarimetric SAR data from forests[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(8): 2583-2592.

朱岱寅(1974-)，男，博士，教授，博士生导师，研究方向：合成孔径雷达信号处理、高分辨率雷达成像，E-mail：zhudy@nuaa.edu.cn。

叶少华(1966-)，男，博士，研究员，研究方向：雷达信号处理、雷达系统。

杨鸣冬(1989-)，男，博士研究生，研究方向：合成孔径雷达信号处理。

宋伟(1980-)，男，博士，高级工程师，研究方向：雷达信号处理、雷达系统

Advances in High Resolution Polarimetric Synthetic Aperture Radar Imaging

Zhu Daiyin1, Yang Mingdong1, Song Wei2, Ye Shaohua2

(1.Key Laboratory of Radar Imaging and Microwave Photonics, Ministry of Education, College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 211106, China;2.AVIC Leihua Electronic Technology Research Institute, Wuxi, 214063, China)

As an effective technology for earth remote sensing, synthetic aperture radar (SAR) provides high-resolution, wide-swath, day-and-night and weather-independent images for observation region, which has been widely used for military reconnaissance, environmental monitoring, geological mapping, et al. With the developments of radar technology and geoscience, more target characteristics are expected to be acquired. Conventional single-polarimetric SAR has been difficult to meet diversified requirements for practical applications. Based on multi-polarization, polarimetric synthetic aperture radar (PolSAR) can obtain target characteristics under different polarization state. PolSAR enriches information of SAR images, whose applications are further expanded. Scattering mechanism interpretation is an important bridge between the collected data and real applications. In this paper, the research progress of PolSAR is firstly reviewed, with emphasis on polarimetric target decomposition. Processing results of real data is presented. Finally, some possible directions for future development are proposed.

polarimetric synthetic aperture radar (SAR); radar imaging; polarimetric target decomposition; scattering mechanism; scattering model

国家自然科学基金(61301210,61301212)资助项目；航空科学基金(20142052020,20142052021)资助项目；江苏省自然科学基金(BK20130815)资助项目；江苏省高校优势学科建设工程资助项目。

2016-06-14；

2016-07-02

TN958

A