智能传感器递推多项式校准方法设计与分析
余学锋,于 杰,张 斌,王 柯
(中国人民解放军63870部队,陕西 华阴 714200)
智能传感器递推多项式校准方法设计与分析
余学锋,于 杰,张 斌,王 柯
(中国人民解放军63870部队,陕西 华阴 714200)
针对智能传感器测量系统校准中线性化的问题,提出了递推多项式校准方法. 分析了校准点选择和排列顺序对递推算法的影响,设计了两种校准点选择模式,即人工设置模式A和自适应选择模式B. 数值计算和实际测试表明,两种模式实施简单、 快捷和准确,但相比模式A,模式B则更加有效地降低了多项式阶数,减少了计算量.
智能传感器; 递推多项式校准; 非线性误差
在智能传感器得到普遍应用的今天,如何校准智能传感器非线性误差成为提高传感器测量系统性能的关键. 智能传感器非线性误差校准主要有硬件补偿法及软件校准法. 硬件补偿法存在补偿效率不高,拓展性差等缺点. 为了充分利用智能传感器具有微处理单元的特点,软件校准法成为主流,特别是对自身特性曲线非线性误差较大的传感器. 目前,软件校准法主要有插值法、 查表法、 曲线曲面拟合法和BP神经网络法[1]. 插值法、 查表法占用大量内存,影响微处理器运算速度,对于非线性误差较大的传感器校准精度有限. BP神经网络法自身存在网络不稳定,训练时间较长的不足,限制了其使用范围,在许多场合下,仍然需要寻求其它方法以达到更好的校准效果[2]. 采用支持向量机校正传感器非线性误差的方法,由于算法中核函数的选择及其参数的确定问题[3],还有待进一步研究. 从工程应用角度来看,较为成熟的方法还是曲线拟合法. 多项式拟合算法具有运算量小,速度快等优点,适合微处理器运算. 但目前多项式拟合还主要是基于最小二乘法,依靠规范化多项式拟合程序[4,5],需要的校准点多,多项式函数阶次较高. 本文提出了一种基于递推多项式的新校准方法,对递推多项式校准方法中涉及的校准点选择和排列顺序等不确定性因素,设计了两种校准点选择模式. 并通过数值仿真和实际测试,给出了经过递推多项式校准后的传感器非线性误差补偿效果.
1 递推多项式校准原理
1.1 基本原理
递推多项式校准属于智能传感器非线性校准技术范畴,其校准过程可以在智能化软件程序的引导下自动实施. 设传感器输入输出函数关系为y=f(x),xi,yi,pi分别为传感器输入参考值、 逼近多项式输出值和校准输出期望值,有:xi=[x1,x2,…,xn],yi=[f(x1),f(x2),…,f(xn)],pi=[p1,p2,…,pn].n为校准点数量. 与传统的基于最小二乘法的多项式拟合校准方法不同,本文设计的递推多项式校准就是先给出一个一次多项式(一般为端点线性函数),然后反复使用灵敏度/增益变化值,使多项式逐渐逼近传感器特性曲线,直到满足非线性误差校准要求. 取线性多项式f(x)=k0x作为起始点,经过零值校准后得到多项式f1=k0x+k1以及校准输出期望值p1. 将校准点x2带入多项式f1中,得到当前校准点下多项式输出值f1(x2)以及校准输出期望值p2,由此可以计算得到灵敏度/增益校准系数k2,经过递推运算产生一个新的多项式f2,依次往复,通过每一个单步迭代过程,将递推中的隐式计算逐步显示化. 其实质就是在对传感器已经调零的基础上,通过改变灵敏度/增益值,使产生的多项式不断逼近传感器特性曲线函数,直到满足传感器独立线性度要求.
可以看出,递推多项式校准方法有几个不确定因素: ① 传感器测量范围内校准点的选择,包括数量、 数值和顺序; ② 校准后能达到的最小非线性误差; ③ 校准方法对传感器的适应性. 由于在递推多项式计算过程中涉及到传感器灵敏度/增益值算法,以及实际校准中校准点数量、 数值和顺序的选择,任何一个因素的微调都会影响最终的校准效果,因此设计了两种递推多项式校准模式,即校准点人工设置模式和自适应选择模式,分别称模式A和模式B,并通过随后的数值计算分析两种模式的技术特点.
1.2 模式A设计
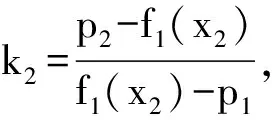
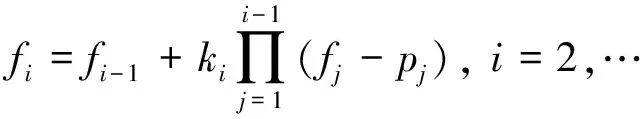
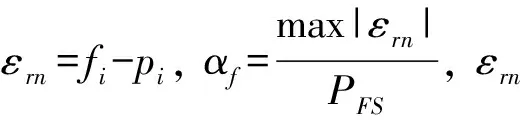
在实际校准中,第一和第二个校准点选择为传感器特性曲线的零点和满量程点,随后的校准点根据传感器量程范围以及校准源实际情况设置3~7个点. 在模式A中不确定因素主要有校准点排列顺序,校准数值选择等,这些受人员经验的影响较大,为此对模式A再寻求是否有改进的可能.
1.3 模式B设计


在模式B中,灵敏度/增益校准系数是采用其绝对变化量进行计算的,除了第一和第二个校准点以外,其它校准点数值是由算法运行过程中自动选择的. 在校准过程中,根据前一次递推多项式函数与传感器实际特性曲线函数差值的最大值所对应的校准点选择下一个校准值. 与模式A相同的是: 在实际校准时,第一和第二个校准点选择为传感器特性曲线的零点和满量程点,而随后的校准点则由校准过程自动选择. 而校准点数量同样是在校准过程中每完成一次校准都要对获得的多项式函数与期望值函数进行误差计算,计算方法同模式A,当满足对传感器校准误差设置要求时校准过程结束. 也就是说,模式B方法不论是校准点数值还是数量都是由校准过程自动选择. 模式A与模式B除了在灵敏度/增益校准系数算法上不同外,在校准点选择上也有很大的不同,这些区别会给校准带来什么样的效果,将通过数值仿真计算给予说明.
2 递推多项式校准方法的数值仿真
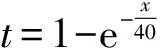
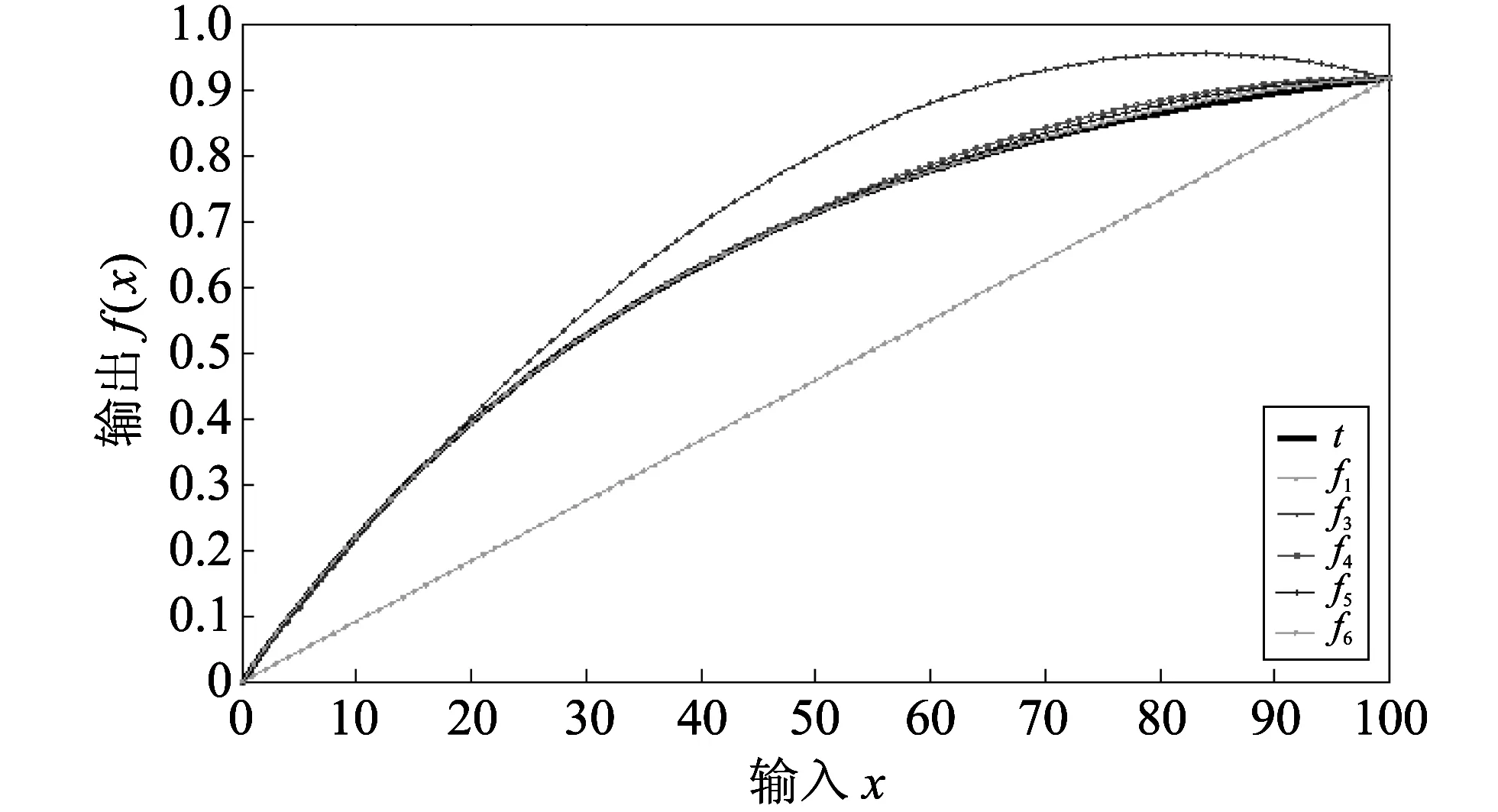
图 1 模式A递推多项式函数曲线(6点)Fig.1 Recursion polynomial function curves of type A (6 point)
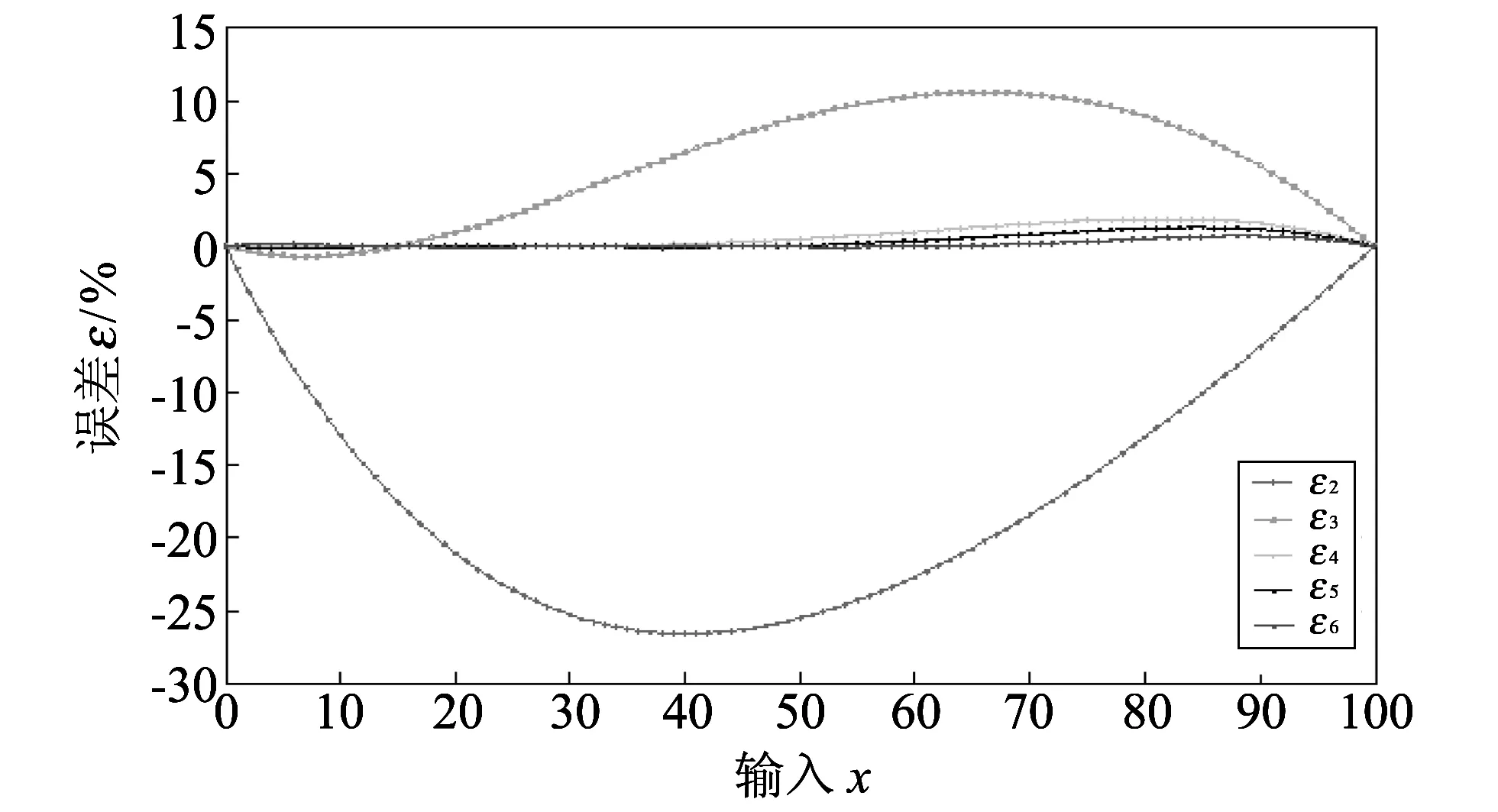
图 2 模式A递推多项式函数误差(6点)Fig.2 Recursion polynomial function error of type A (6 point)
从数值仿真计算结果可以看出: 对于模式A,当完成6个点校准后,获得的多项式函数曲线逼近模拟传感器特性曲线,其非线性误差为0.29%; 而对于模式B,当完成6个点校准后,获得的多项式函数曲线逼近模拟传感器特性曲线,其非线性误差为0.012%.
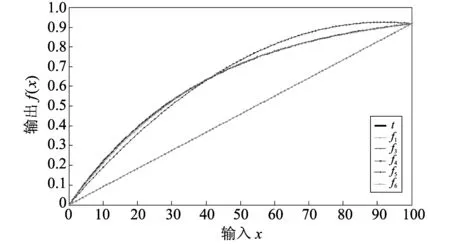
图 3 模式B递推多项式函数曲线(6点)Fig.3 Recursion polynomial function curves of type B (6 point)
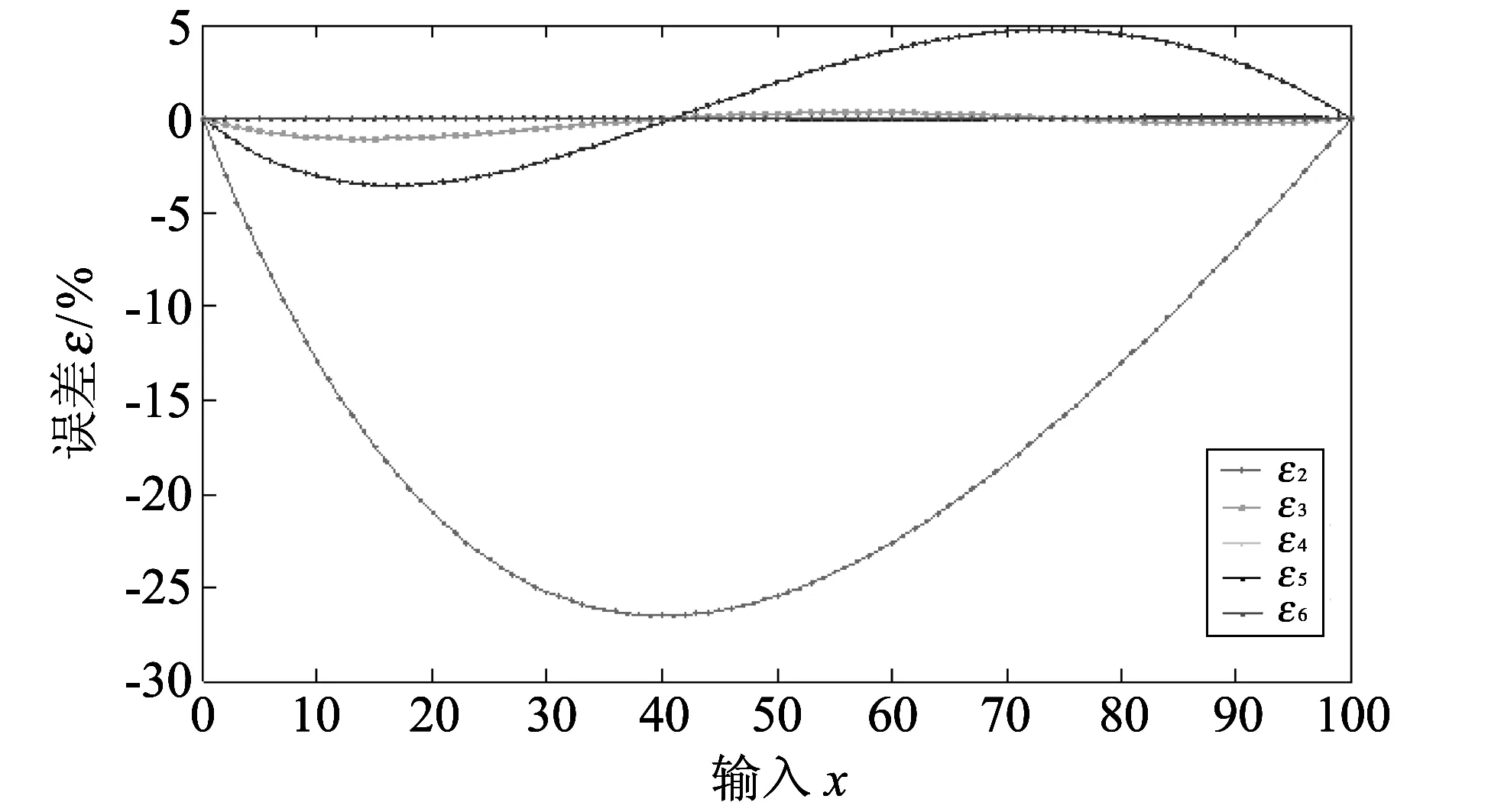
图 4 模式B递推多项式函数误差(6点)Fig.4 Recursion polynomial function error of type B (6 point)
更进一步的数值仿真计算结果如表 1 所示,可以看出,传感器特性曲线非线性误差范围从48.35%~12.96%,模式A完成6个点校准后相应的非线性误差为4.91%~0.009%. 模式B完成6个点校准后相应的非线性误差为0.27%~0.002%. 对于某一给定的特性曲线(28.49%),模式B只用5个校准点就能达到模式A所需6个点的效果. 也就是说在同等条件下,模式B有效降低了多项式阶数. 而基于最小二乘法的多项式拟合,通常需要16个校准点才能达到独立线性度优于0.5%的效果[6](特性曲线非线性误差为28.49%时).
表 1 数值仿真计算结果
Tab.1 The results of numerical simulation calculation

模拟函数端点连线线性度/%模式A校准独立线性度%5点6点7点模式B校准独立线性度%5点6点7点48.357.684.911.952.130.270.0612.960.140.0090.0030.0080.0020.00128.491.310.290.210.110.0120.008
同时,模式A对设置的校准点排列顺序较为敏感,对于给定的特性曲线(28.49%),同样的6个点,采用不同的排列顺序(排列组合略),其校准非线性误差变化范围为0.29%~1.52%,因此对模式A而言存在最优校准点排列设置. 模式B在校准点选择上,除了开始两个点以外,其余校准点都是在校准过程中由算法自动选择,因此模式B在校准点选择上更为优化. 两种模式校准误差与校准点的数量也有一定的关系,随着校准点的增加,校准误差也逐步减少,但校准点达到8个以后,误差减少就不明显了.
通过数值仿真计算可以看出: 采用模式A,对于端点连线线性度小于28%的传感器特性曲线,通过6点校准可使得该传感器的独立线性度优于0.5%; 而采用模式B,对于端点连线线性度小于48%的传感器特性曲线,通过6点校准可使得该传感器的独立线性度优于0.5%. 综合而言,在多项式拟合方法的工程应用中,如果校准源选择允许,递推多项式模式B方法应作为智能传感器非线性误差校准的首选.
3 实际应用
某型低成本温度测量系统,其中温度传感器采用了NTC型热敏电阻[7]. 该热敏电阻传感器的热敏指数B=4 100,基准温度T0=25 ℃,标定阻值R0=10 kΩ. 将温度测量系统中需要校准的NTC热敏电阻与二等铂电阻温度标准同时放入干式校准炉中,FLUKE9103干式校准炉可提供-25~140 ℃范围的温度,各点温度可预先设定控制,也可程序控制,二等铂电阻温度标准作为温度参考. NTC热敏电阻测得的温度值经过微处理器运算后,通过RS232接口传入计算机显示. 校准方法如图 5 所示.
选择校准温度范围为-20~100 ℃,在这个范围内选择6个校准点. 对于模式A,校准点为:Ti=[-20 ℃,100 ℃,0 ℃,25 ℃,50 ℃,75 ℃]; 对于模式B,第一第二个校准点为-20 ℃和100 ℃,随后采用自适应算法自动选择校准点,校准过程显示的校准点为:Ti=[-20 ℃,100 ℃,78 ℃,57 ℃,42 ℃,10 ℃],校准结果如表 2 所示. 通过校准,使得温度测量系统中的NTC热敏电阻特性曲线非线性误差由29.6%减少至0.5%以下(6点),同时可以看出,达到同样的误差要求,模式B比模式A需要更少的校准点.

表 2 温度测量系统校准结果
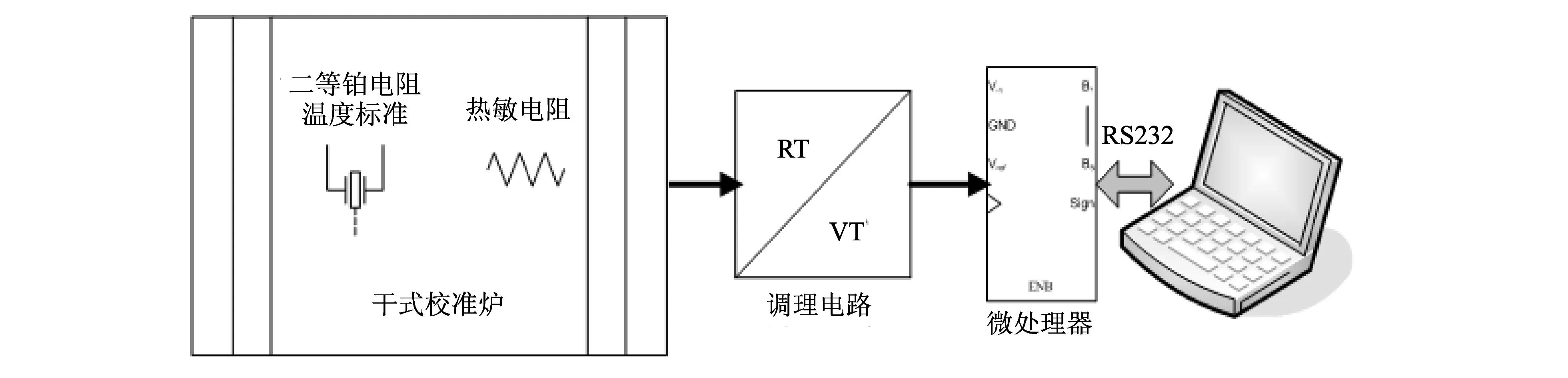
图 5 温度测量系统校准示意图Fig.5 Schematic of temperature measurement system calibration
4 结 论
递推多项式校准方法通过逐步调整灵敏度/增益系数,使产生的多项式不断逼近传感器特性曲线函数. 只要知道被校目标传感器的最大量程范围,就可根据模式A或模式B的方法选择校准点数量,以最少的时间实现传感器非线性误差校准. 模式B更是在模式A的基础上,通过校准点自动选择,有效降低了多项式函数的阶数,减轻了微处理器的计算量.
在递推多项式校准中,递推算法简洁,易于编程,占用存储空间小,非常适于微处理器运算,数值仿真计算和实际应用表明,只要智能传感器的端点连线线性度在48%以内,递推多项式6点校准就可实现传感器的独立线性度优于0.5%的结果,具有良好的工程应用前景.
[1] 刘君华. 智能传感器系统[M]. 西安: 西安电子科技大学出版社, 1999.
[2] 田社平,赵阳,韦红雨,等. 基于BP神经网络的传感器非线性补偿[J]. 测试技术学报, 2007, 21(1): 86-89. Tian Sheping, Zhao Yang, Wei Hongyu, et al. Nonlinear compensation of sensors based on BP neural network[J]. Journal of Test and Measurement Technology, 2007, 21(1): 86-89. (in Chinese)
[3] 周鸣争, 汪军. 基于支持向量机的传感器非线性误差校正[J]. 电子科技大学学报, 2006, 35(2): 242-245. Zhou Mingzheng, Wang Jun. Nonlinear error correction of sensors based on support vector machine[J]. Journal of UEST China, 2006, 35(2): 242-245. (in Chinese)
[4] 周伟, 包建东, 丁良华. 传感器标定的非线性校正研究[J]. 测试技术学报, 2013, 27(4): 358-361. Zhou Wei, Bao Jiandong, Ding Lianghua. Nonlinear correction of sensor calibration[J]. Journal of Test and Measurement Technology, 2013, 27(4): 358-361. (in Chinese)
[5] 沈金鑫, 夏静. 硅压阻式压力传感器智能校准系统设计[J]. 仪表技术与传感器, 2014(3): 1-3. Shen Jinxin, Xia Jing. Intelligent calibration system design of silicon piezoresistive pressure sensor[J]. Instrument Technique and Sensor, 2014(3): 1-3. (in Chinese)
[6] 赵岩, 李永红, 王恩怀. 基于MAX1452的MEMS压力传感器校准系统的设计[J]. 仪表技术与传感器, 2009(10): 94-96. Zhao Yan, Li Yonghong, Wang Enhuai. Calibration system of MEMS presscure sensor with MAX1452[J]. Instrument Technique and Sensor, 2009(10): 94-96. (in Chinese)
[7] 李兵尚, 施建礼, 吴非,等. 宽温范围测量时NTC热敏电阻器R /T数学模型[J]. 传感器与微系统, 2012, 31(6): 53-55. Li Bingshang, Shi Jianli, Wu Fei, et al. R/T mathematic model of NTC thermistor for wide-temperature-range measuring[J]. Transducer and Microsystem Technologies, 2012, 31(6): 53-55. (in Chinese)
Design and Analysis of Recursion Polynomial Calibration Method for Smart Sensors
YU Xuefeng, YU Jie, ZHANG Bin, WANG Ke
(Unit 63870, PLA, Huayin 714200, China)
By analyzing linearization in smart sensors measurement systems calibration, in this paper, a recursion polynomial calibration method was proposed. Selection and sequence the numbers of Selection and sequence calibration points were analyzed which can affect the recursion algorithms. Two types of calibration points selection were designed, that is, type A and type B. For type A, calibration points were set manually. For type B, those were chosen by intelligent algorithm. Numerical analysis calculation and experimental results show that both types are simple, accurate and less time consuming. But in comparison with type A, type B can eliminate the high degree of produced polynomial effectively and reduce calculation amount.
smart sensors; recursion polynomial calibration; nonlinearity error
1671-7449(2016)06-0523-05
2016-03-17
余学锋(1963-),男,高级工程师,硕士,主要从事仪器仪表与计量测试的研究.
TP212
A
10.3969/j.issn.1671-7449.2016.06.013

