一种基于身份可认证两方密钥协商方案
曹 阳, 邓方安, 陈 涛, 潘 平
(陕西理工大学 数学与计算机科学学院,陕西 汉中 723000)
一种基于身份可认证两方密钥协商方案
曹 阳, 邓方安, 陈 涛, 潘 平
(陕西理工大学 数学与计算机科学学院,陕西 汉中 723000)
为了降低计算开销,提高安全性,通过Diffie-Hellman协议建立密钥共享, 结合用户身份信息,以VBNN_IBS签名思想作为基础,提出了一种可认证的两方密钥协商方案。密钥生成中心KGC结合用户身份信息仅为用户生成部分私钥和公钥,其完整的私钥和公钥由用户结合自己的长期私钥生成,安全性基于椭圆曲线离散对数问题。方案中无双线性对运算,只需椭圆曲线上4次点乘运算、1次模运算、3次哈希运算,通信双方只需2次通信就可实现双方认证和密钥协商,提高了密钥产生的效率。分析表明,该方案具有完美前向保密性、抗密钥泄露伪装攻击、已知会话密钥通信安全、非密钥控制、抗重放攻击等安全属性。性能及安全性比较表明,该方案在安全性和性能方面具有较大的优势,适用于资源受限的无线网络通信环境中。
签名方案;椭圆曲线;身份认证;密钥协商
密钥协商[1-2]是密钥管理的重要组成部分,通过密钥协商可使多个用户在不安全信道上通信协商生成安全共享会话密钥。密钥协商设计思想提出以来,针对其安全性问题,大量学者对其进行研究,并取得了很多成果。如:基于传感器网络提出了一种密钥管理方案[3];为了降低公钥加密的计算开销提出了无双线性对的无证书密码体制[4],但运算量较大;无双线性对的认证密钥协商方案[5-6];利用身份加密建立了无线网络密钥协商方案[7-8],但计算开销较大;无证书两密钥协商方案除去了双线性对运算[9],但该方案不能实现双向认证;协商方案无双线性对运算[10],但每次协商需要4次通信;文献[11]提出的方案效率虽然提高了,但每次协商需要3次通信;无证书密钥协商方案[12]存在双线性对运算。本文基于认证、通信等问题,基于用户身份,以椭圆曲线离散对数问题(elliptic curve discrete logarithm problem[13])的安全性作为保证,通过Diffie-Hellman协议建立密钥共享,以BNN-IBS[14]的变形方案VBNN-IBS[15]为基础,结合用户身份信息,提出了一种可认证的两方密钥协商方案。本方案的运算量低,通信双方只需2次通信就可实现双向认证和密钥协商,具有完美前向保密性、抗密钥泄露伪装攻击、已知会话密钥通信安全等安全属性。
1 背景知识
定义1(椭圆曲线):有限域Fq上的椭圆曲线[13,16]E(Fq)是满足a,b∈Fq,Δ=4a3+27b2≠0 modq的曲线:y2=x3+ax+b。无穷远点o与E(Fq)上的点构成n阶群,G为E(Fq)上的基点,p为G的阶,p为大素数,满足p2不被n整除,G1为由G生成的循环群。
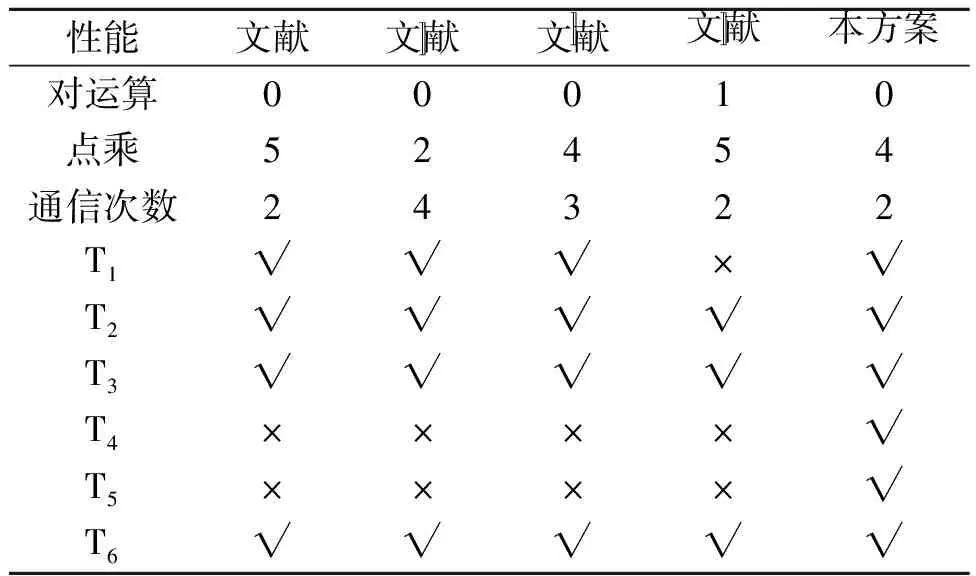
定义2(椭圆曲线离散对数问题[13]):如果存在整数l(0 定义3(完美前向保密性[3]):如果所有参与者的长期私钥泄漏,已建立的会话密钥不会被攻破[3],即攻击者不能有效计算出旧的会话密钥。 定义4(抗密钥泄露伪装攻击[3]):获得了用户UIDA的长期私钥xA和临时私钥aA的攻击者只具有冒充用户UIDA的能力,即攻击者不能伪造其他用户与用户UIDA生成会话密钥[3]。 定义5(已知密钥安全[3]):每一次密钥协商过程中,密钥协商双方都能独立生成唯一的共享会话密钥[3],即其他会话密钥的泄露不会影响密钥的安全性。 定义6(非密钥控制[3]):任何用户都不能强制会话密钥是一个预先确定的值。 定义7(未知密钥共享[3]):在用户UIDA不知道的情况下,不能强制用户UIDA与用户UIDB共享一个会话密钥。 Bellar等[14]利用椭圆曲线上的点乘运算,基于身份信息,提出了一种签名方案——BNN_IBS[14]签名方案,并对其安全性作了证明。CAO 等[15]为了将BNN_IBS签名方案的签名长度由105 byte减少到83 byte,提出了BNN_IBS的变形方案——VBNN_IBS[15]签名方案。VBNN_IBS方案描述如下。 a.选取系统参数 b.生成用户密钥 c.签名 d.验证 根据公开参数、用户UIDi、消息m的签名〈R,h,Q〉,计算c=H1(UIDi‖R),验证h=H2(UIDi,m,R,QG-h(R+cK))是否成立。若成立,则接收消息,否则放弃。 方案主要包括初始化、用户密钥生成、密钥协商3个部分。为了进一步增加方案的安全性,在用户密钥生成时增加了长期私钥和临时私钥。 3.1 初始化 3.2 用户密钥生成 3.3 密钥协商 c.用户UIDA收到〈UIDB,EB,hB,QB,SB,fB〉后,判断nonce是否是自己发送给用户UIDB的,nonce=fB⊕SB⊕UIDB。如果是,则计算cB=H1(UIDB‖SB),并验证hB=H2(UIDB,EB,QB,QBG-hB(SB+SBcBK))是否成立。如果成立,说明用户UIDB的身份合法。计算KAB=bAEB,会话密钥为SKAB=H2(UIDA‖UIDB‖KAB)。 4.1 正确性分析 证明1: Ri+H1(UIDi‖Ri)K=Ri+H1(UIDi‖Ri)kG =riG+H1(UIDi‖Ri)kG =(ri+cik)G =diG 证明2: hA=H2(UIDA,EA,QA,QAG-hA(SA+SAcAK)) =H2(UIDA,EA,QA,QAG-hA(SA+SAcAK)) =H2(UIDA,EA,QA,(aA+hAsA)G-hA(SA+SAcAK)) =H2(UIDA,EA,QA,aAG+hAsAG-hA(SA+SAcAK)) =H2(UIDA,EA,QA,YA+hAxAdAG-hA(SA+SAcAK)) =H2(UIDA,EA,QA,YA+hAxA(rA+CAk)G-hA(SA+SAcAK)) =H2(UIDA,EA,QA,YA+hA(xARA+xARAcAK)-hA(SA+SAcAK)) =H2(UIDA,EA,QA,YA+hA(SA+SAcAK)-hA(SA+SAcAK)) =H2(UIDA,EA,QA,YA) =hA 证明3: KAB=bAEB=bAbBG=bBEA=KBA 由证明1知,用户验证KGC分配给自己的私钥有效性是正确的;由证明2知,密钥协商双方身份认证是正确的;由证明3知,密钥协商双方得出的会话密钥是相同的。因此,方案是正确的。 4.2 方案安全性分析 4.2.1 抗密钥泄露伪装攻击 4.2.2 完美前向保密性 方案中共享密钥SKAB=H2(UIDA‖UIDB‖KAB)=H2(UIDA‖UIDB‖KBA)是由椭圆曲线和哈希函数实现密钥协商双方身份认证得到的。由3.3密钥协商过程知,EA=bAG,EB=bBG,其中bA、bB是用户选取的随机数,如果攻击者想从EA、EB计算出bA、bB,难解性基于椭圆曲线离散对数问题。由于共享密钥是由随机数确定,每一轮密钥协商所选取的随机数都不同,即使密钥协商双方的私钥泄露或系统主密钥泄露,密钥双方共享会话密钥的安全性也不会被影响。因此方案具有完美的前向保密性。 4.2.3 已知会话密钥安全性 如果攻击者得到以前的会话密钥,但也无法得到本次及将来协商的会话密钥。因为方案中用户密钥是由系统生成的部分密钥和用户长期私钥构成,bA、bB、xA、xB用户选取的是随机数,即方案具备已知会话密钥安全性。 4.2.4 非密钥控制安全性 由SKAB=H2(UIDA‖UIDB‖KBA),KAB=KBA知,会话密钥的计算中只包含了UIDA、UIDB、KAB、KBA信息,KAB、KBA是由用户选取的随机数生成,H2是哈希函数。由于用户每一轮选取的随机数都不同,使得任何用户都没有办法使会话密钥是一个预先确定的值。即方案具有非密钥控制安全性。 4.2.5 抗重放攻击 方案中,加入了新鲜数nonce,通过判断nonce的有效性可以防止重放攻击。 4.2.6 未知密钥共享安全性 方案中,计算会话密钥的哈希函数包含了密钥协商双方的身份,且双方在计算会话密钥前通过等式hi=H2(UIDi,Ei,Qi,QiG-hi(Si+SiciK))进行身份认证,也就不会出现一方在不知道的情况下与另一方进行会话密钥共享。即本方案具有未知密钥共享的安全性。 4.3 开销分析 4.3.1 计算开销 方案中无双线性对运算,主要用到点乘运算、模运算、哈希运算,密钥协商双方通信的次数为2次。用l表示1次点乘运算,m表示1次模运算,h表示1次哈希运算,由2.3知,一次密钥协商过程中密钥协商双方运算量各为(4l+m+3h)。 4.3.2 存储开销 方案中要求预装系统的参数、用户身份信息、建立密钥配对的参数。由于密钥分配的随机性及用户的随机性,系统必须为用户存储相关信息,密钥也可能出冗余,对存储空间的利用率还需要进一步完善,下一步的工作就是在此基础上研究空间的利用率问题。 4.4 性能及安全性比较 方案的性能主要从密钥协商双方通信的次数、点乘次数、是否存在对运算3个方面考虑,安全性方面主要从抗密钥泄露伪装攻击、已知会话密钥安全性、完美前向保密性、未知密钥共享安全性、双向认证、非密钥控制安全性6个方面与引言中提到的文献[9-12]相比较。性能及安全性比较如表1所示。其中“数字”表示次数;“√” 表示具有该方面的安全性;“×”表示不具有该方面的安全性;“T1”代表抗密钥泄露伪装攻击;“T2”代表已知会话密钥安全性;“T3”代表完美前向保密性;“T4”代表未知密钥共享安全性;“T5”代表双向认证;“T6”代表非密钥控制安全性。 表1 性能及安全性比较 Table 1 Comparison of performance with security 性能文献文献〛文献〛文献〛本方案对运算00010点乘52454通信次数24322T1√√√×√T2√√√√√T3√√√√√T4××××√T5××××√T6√√√√√ 本文提出的密钥协商方案无双线性对运算,密钥生成中心KGC结合用户身份信息生成的私钥、公钥只能作为用户的部分私钥和部分公钥,完整的私钥、公钥由用户自己生成,仅需2次通信就可实现通信双方的认证和密钥协商,且通信双方运算量各为(4l+m+3h),提高了认证和密钥产生的效率。安全分析表明,方案具有抗重放攻击、完美前向保密性、抗密钥泄露伪装攻击等属性。性能及安全性比较表明,该方案在安全性和性能方面具有较大的优势,较适用于资源受限的无线网络通信环境中。 [1] Chan H, Perring A, Song D. Random key predistribution schemes for sensor networks [C]//Proc of the 2003 IEEE Symp on Security and Privacy. Washington: IEEE Computer Society, 2003: 197-213. [2] Eschenauer L, Gligor V. A key management scheme for distributed sensor networks[C]//Proc of the 9th ACM Conf on Computer and Communications Security. New York: ACM Press, 2002: 41-47. [3] 袁艳祥.基于身份的密钥管理研究[D].杭州:杭州电子科技大学档案馆,2013. Yuan Y X. Identity-based Key Management[D]. Hangzhou: The Archive of Hangzhou Dianzi University, 2013. (In Chinese) [4] Baek J, Safavi-Naini R, Suailo W. Certificateless public key encryption without paring[C]// LNCS3650: Proceedings of the 8th International Conference on Information Security(S.l). Berlin: Springer-Verlag, 2005: 134-148. [5] 朱辉,李晕,谭示崇,等.不使用双线性对的无证书认证协议[J].武汉大学学报:信息科学版,2010,35(5):574-577. Zhu H, Li Y, Tan S C,etal. Certificateless authentication protocol without pairing[J]. Geomatics and Information science of Wuhan University, 2010, 35(5):574-577. (In Chinese) [6]Geng M, Zhang F. Provably secure certificateless two-party authenticated key agreement protocol without pairing[C]//Proceedings of the International Conference on Computational Intelligence and Security, CIS’09[S.l.]. Washington: IEEE Computer Society, 2009: 208-212. [7] 郭江鸿,李兴华,武坚强.一个新的基于身份的无线传感器网络密钥协商方案[J].计算机科学,2011,38 (3):127-130. Guo J H, Li X H, Wu J Q. New identity-based key agreement scheme for WSN[J]. Computer Science, 2011, 38(3): 127-130. (In Chinese) [8] 程宏兵,费国臻.基于身份的无线传感器网络密钥系统[J].计算机科学,2007,34(10):116-119. Cheng H B, Fei G Z. Research of identity-based key system scheme for wireless sensor network[J]. Computer Science, 2007, 34(10): 116-119. (In Chinese) [9] 刘文浩,许春香.无证书两方密钥协商方案[J].软件学报,2011,22(11):2843-2852. Liu W H, Xu C X. Two party certificateless key agreement schemes[J]. Journal of Software, 2011, 22(11): 2843-2852. (In Chinese) [10] 潘进,刘小琼,李国朋.无双线性对的无证书两方认证密钥协商协议[J].计算机应用研究,2012,29(6):2240-2243. Pan Jin, Liu X Q, Li G P. Certificateless-based two-party authenticated key agreement protocol[J]. Application Research of Computers, 2012, 29(6): 2240-2243. (In Chinese) [11] 曹雪菲,寇卫东,樊凯,等.无双线性对的基于身份的认证密钥协商协议[J].电子与信息学报,2009,31(5):1241-1244. Cao X F, Kou W D, Fan K,etal. An identity-based authenticated key agreement protocol without bilinear pairing[J]. Journal of Electronics & Information Technology, 2009, 31(5): 1241-1244. (In Chinese) [12] 朱志馨,董晓蕾.高效安全的无证书密钥协商方案[J].计算机应用研究,2009,26(12): 4787-4790. Zhu Z X, Dong X L. Efficient and secure certificateless key agreement protocol[J]. Application Research of Computers, 2009, 26(12): 4787-4790. (In Chinese) [13] 曹阳,洪歧,陈勇,等.一种基于ECC具有时间限制的动态秘密共享方案[J].重庆邮电大学学报(自然科学版),2014,26(4):556-558. Cao Y, Hong Q, Chen Y,etal. A time-limited dynamic secret-sharing scheme based on ECC[J]. Journal of Chongqing University of Posts and Telecommunications, 2014, 26(4): 556-558. (In Chinese) [14] Bellare M, Namprempre C, Neven G. Security proofs for identity-based identification and signature schemes[J]. Journal of Cryptology, 2009, 22(1): 1-16. [15] Cao X, Kou W, Dang L,etal. IMBAS: Identity-based multi-user broadcast authentication in wireless sensor networks[J]. Computer Communications, 2008, 31: 659-671. [16] 郭松辉,牛小鹏,王玉龙.一种基于椭圆曲线的轻量级身份认证及密钥协商方案[J].计算机科学,2015,42(1):137-141. Guo S H, Niu X P, Wang Y L. Elliptic curve based light-weight authentication and key agreement scheme[J]. Computer Science, 2015, 42(1): 137-141. (In Chinese) A two-party key agreement scheme based on authenticated identity CAO Yang, DENG Fang-an, CHEN Tao, PAN Ping SchoolofMathematicsandComputerScience,ShaanxiSci-techUniversity,Hanzhong723000,China Based on the establishment of shared key through the Diffie-Hellman agreement in terms of the user’s identity information and combined with VBNN-IBS signature thought as a foundation, a two-party key agreement scheme is proposed so as to reduce the computation cost and improve the security. In the scheme, the key generation centre (KGC) uses users’ identity information to generate part of the private and public keys for the two parties in communication. The complete private key and public key are composed of users’ private key for a long time, and the security is based on elliptic curve discrete logarithm problem. The no-bilinear paring operation is realized only by four times point multiplication operation, one modular operation, and three times hash operations. Meanwhile, the two parties in communication can realize the authentication and key agreement only by communication twice, which improves the efficiency of the key generation. It shows that the scheme possess a lot of safety properties, such as perfect forward secrecy, resisting key leak feinting, known session key communications security, non-key control, and anti-replay attacks capacity, etc. The comparison of performance with security reveals that the scheme has great advantages in terms of safety and efficiency. Therefore, it is suitable for the resource-constrained wireless network communication environment. signature scheme; elliptic curve; identity authentication; key agreement 10.3969/j.issn.1671-9727.2016.06.14 1671-9727(2016)06-0757-05 2015-05-25。 [基金项目] 国家自然科学基金项目(21373132); 陕西省教育厅资助项目(16JK1149)。 [第一作者] 曹阳(1978-),女,硕士,讲师,研究方向:信息安全与计算机应用, E-mail:cyang0618@sina.com。 TP309 A2 VBNN_IBS签名方案

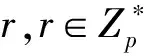

3 密钥协商方案



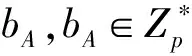

4 方案分析

5 结 论

