合成射流激励位置对控制翼型大攻角分离流动影响的数值研究

兰艾青,王志恒,于洪石,席光

(西安交通大学能源与动力工程学院,710049,西安)



合成射流激励位置对控制翼型大攻角分离流动影响的数值研究

兰艾青,王志恒,于洪石,席光

(西安交通大学能源与动力工程学院,710049,西安)

针对合成射流的激励位置这一因素,以NACA0015翼型为研究对象,对大攻角(α=20°)下基于弦长的Re为8.96×105、单个合成射流激励位于翼型吸力面不同位置时的流场进行了二维非定常计算,并利用本征正交分解(POD)方法对计算结果进行了分析,阐释了相关控制机理。研究表明,合成射流的激励位置对翼型流动分离的控制效果有显著影响。当激励位置位于0.12至0.4倍弦长之间时,合成射流激励能有效抑制翼型流动分离,提升升力系数,降低阻力系数,升阻比最高提升293%,其中最优激励位置并不在普遍认为的控制前时均分离点附近,而在离分离点下游一定距离的分离区内部。对计算结果的POD分析表明,合成射流的引入改变了流场不同模态间的能量分配,能量由代表平均流动的一阶模态向代表流场中湍流大尺度结构的二阶及更高阶模态转移。合成射流的最佳激励位置与控制前流场二阶模态翼型吸力面附近的特征涡结构有关,要达到最佳的控制效果,合成射流激励应放置在特征涡结构的位置,若布置在下游或者较远的上游位置,则无控制效果。

合成射流;翼型流动分离;激励位置;本征正交分解

在大攻角流动下翼型表面会出现明显的流动分离现象,使得翼型升力迅速降低,阻力陡然升高,同时非定常的流场波动也会引起噪声和振动。合成射流是一种新型的主动流动控制技术,相对襟翼[1]、涡流发生器[2]等被动控制技术,其能更加灵活地应对变化的来流条件,具有无需外部气源、结构紧凑、能耗低、响应快等优势[3-5],Glezer等[6]将其应用到流动控制领域后受到了众多研究者的关注。

合成射流又称为零质量射流,它能够通过体积压缩或者变温的方式改变激励器腔体压力,在激励器出口处形成周期性的吹吸气。合成射流与边界层的相互作用可以改变边界层的速度分布,加强边界层与主流的掺混,从而实现对翼型绕流的控制。合成射流激励位置代表了控制的空间特性,如果该位置布置不当,很难取得良好的控制效果,更无法进一步优化频率、速度等参数。在以往的研究中合成射流布置位置不尽相同,部分将合成射流放置在翼型尾缘[7-9],多数将合成射流布置在翼型中前部。Seifert等实验研究表明,翼型的激励器最佳位置与翼型无控制时的分离点重合[10]。He等研究表明,当合成射流被放置在分离点附近时有最好的控制效果[11]。Raju等指出,将合成射流布置在分离区内部无法提高升阻比[12]。李玉杰等的研究表明,合成双射流激励器越靠近分离点,其对边界层分离的控制效果越好[13]。Chapin等研究对最优控制位置有不同的结论[14],他们发现分离区内部某位置对分离有更显著的影响。Duraisamy等对旋转的NACA0015翼型的分离控制研究发现,攻角从14.7°到19°变化时,合成射流位于距时均分离点较远的下游某位置也能缓解分离并实现分离流动再附[15]。

本文针对大攻角(α=20°)下NACA0015翼型的分离流动,计算了单个合成射流施加在不同位置时的翼型流场,研究了激励位置对合成射流控制效果的影响,运用本征正交分解(POD)方法对计算得到的非定常流场进行了分析,阐释了合成射流激励位置影响控制效果的流动机理。

1 计算模型和参数设置

1.1 数值方法

采用Fluent软件,通过求解二维、不可压缩、非定常时均Navier-Stokes方程模拟了绕翼型流动。空间离散采用二阶格式,时间离散采用一阶隐式格式。为了保证足够的时间分辨率,时间步长Δt=4×10-5s。求解器采用PISO方法对压力、速度进行耦合。

湍流模型采用SSTk-ω模型,以模拟逆压梯度和流动分离。Rehman等对NACA0015的数值模拟结果表明,分离较大时,相对于k-ε模型和S-A模型,SSTk-ω模型具有更好的精度和算法稳定性[16]。

1.2 计算模型

研究对象为NACA0015翼型,来流攻角α=20°,计算域为图1所示的C型区域,C型区域中心为NACA0015翼型,远场距离为15倍弦长。参照Gilarranz等的实验设置[17],数值模拟中取翼型的弦长c为0.375 m,来流速度U∞为35 m/s,基于弦长的雷诺数Re=8.96×105的合成射流出口宽度h=2 mm。

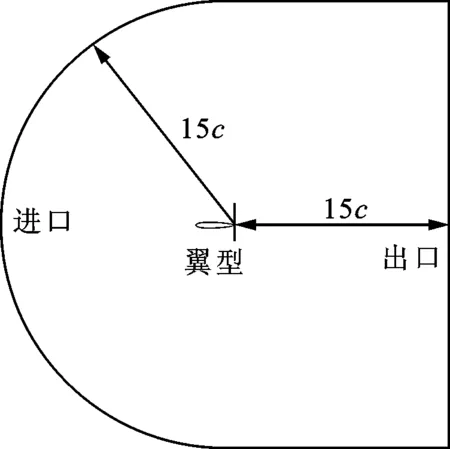
图1 计算模型

除合成射流出口之外的翼型壁面采用无滑移绝热边界条件,远场进口采用速度入口边界条件,出口采用压力出口边界条件。在翼型表面Sjet处的合成射流出口采用周期性速度入口边界条件[18],如图2所示。合成射流出口速度

(1)

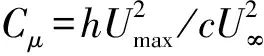
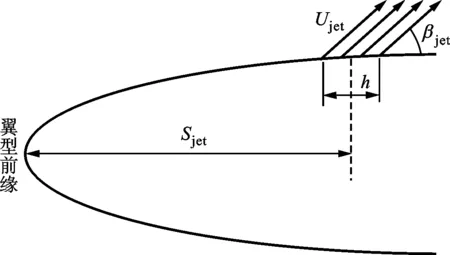
图2 周期性速度入口边界条件示意图

1.3 网格

计算时采用的结构化网格如图3所示。为保证边界层内的法向节点数不低于20,对翼型表面流动边界层区域进行了加密;为保证单个合成射流激励位于不同位置时计算的网格拓扑结构一致,对本文翼型从前缘到尾缘的11个不同的合成射流位置进行了局部加密。壁面第一层网格的长度为10-5c,绝大部分壁面区域的Y+<1,总网格数为104 664。

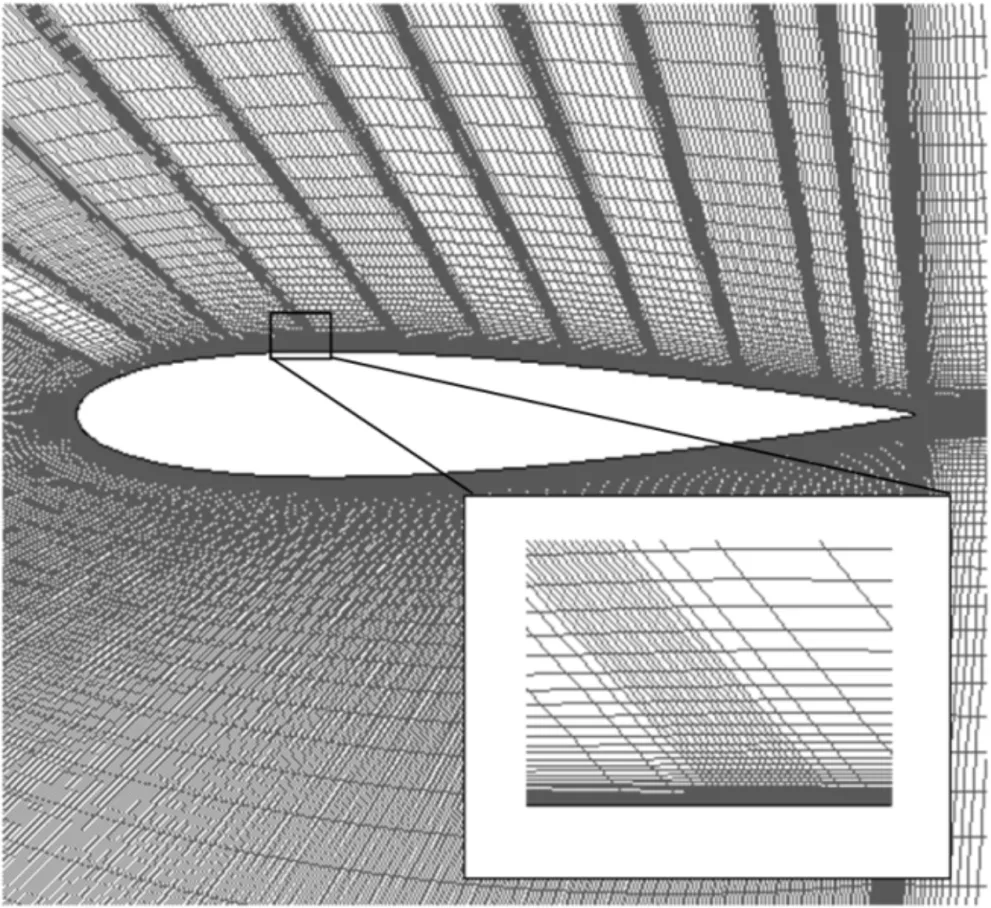
图3 计算网格

1.4 数值模型检验

本文计算了α=19.4°时的无控制流场,并将计算结果与实验数据[12]进行了对比。α=19.4°时翼型表面压力系数分布的对比如图4所示。可以看出,除翼型的吸力面分离区外,其他部分计算结果和实验基本吻合。翼型吸力面区域出现差异说明数值模型预测的流动分离与实际有一定偏差,这是由湍流模型的局限性造成的。总体而言,本数值计算模型可以较准确地模拟攻角临近20°时的翼型绕流。

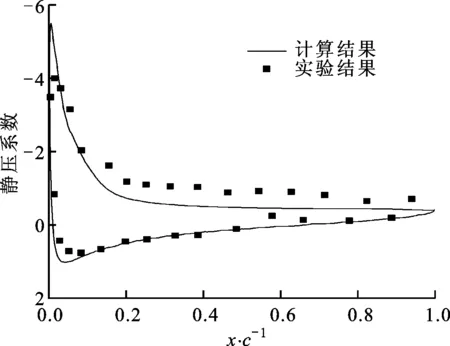
图4 α=19.4°时翼型表面压力系数分布

2 合成射流位置对气动性能的影响

在上述数值模型的基础上,针对α=20°分别计算了无控制时和合成射流布置在翼型上表面Sjet/c=0.05～0.95之间的11个不同位置时的翼型流场。

单个合成射流布置在不同位置时的时均升阻比如图5所示。Sjet/c=0.12～0.4为有效控制区,升阻比明显提升,其中Sjet/c=0.3～0.4时提升最大,为最优控制区。靠近前缘的Sjet/c=0.05,以及从翼型中部Sjet/c=0.5直至尾缘附近的Sjet/c=0.95均为无效控制区,升阻比相比控制前几乎无提升,甚至在靠近尾缘处翼型性能下降。在翼型中部Sjet/c为0.4～0.5之间出现了升阻比的骤然下降。虽然在原流场分离点附近的合成射流激励能够有效减小分离,但是最优的控制位置却位于分离区内部。

图5 时均升阻比随合成射流激励位置的变化

不同合成射流激励位置的时均升力系数和阻力系数分别如图6和图7所示。从图6看出:当激励位置靠近前缘的Sjet/c=0.05时,升力系数略有增加;随着激励位置的后移,升力系数逐渐增大,在Sjet/c=0.4达到最优;从Sjet/c=0.4到Sjet/c=0.5,升力系数显著下降;当Sjet/c=0.5～0.8,升力系数随着位置的后移略有下降,并在靠近尾缘的Sjet/c=0.95处有所回升。从图7看出:当Sjet/c=0.05～0.3,阻力系数逐渐下降;Sjet/c=0.4相对Sjet/c=0.3阻力系数略有提升,但仍优于其他位置;当激励位置从Sjet/c=0.4变化到Sjet/c=0.5时,阻力系数显著上升,此后一直到尾缘,阻力系数随着位置的后移逐步上升。这是因为控制点越靠近尾缘,对分离区产生影响的能力越低,对压差阻力的影响越小,甚至会因为影响尾迹区的掺混使得阻力系数相比控制前上升。

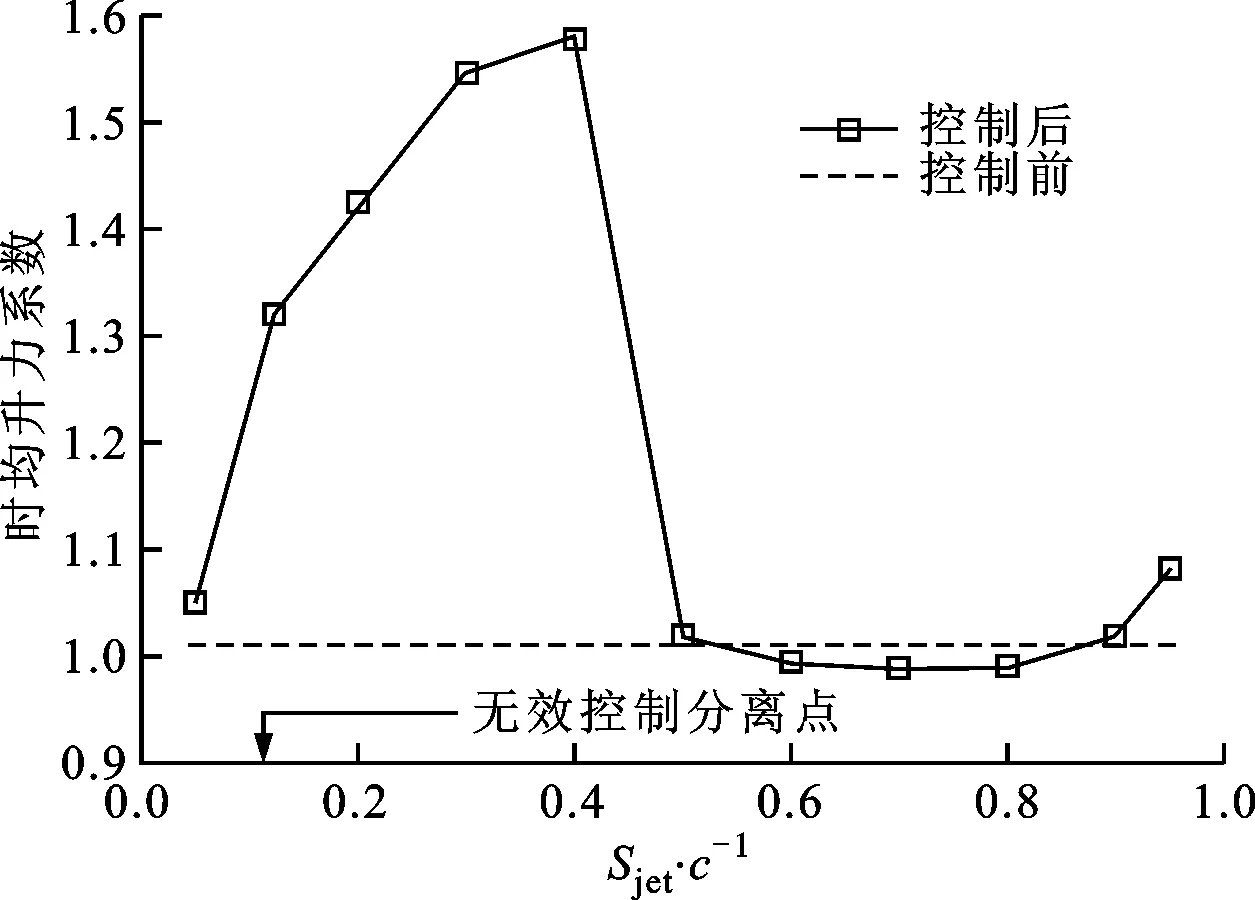
图6 时均升力系数随合成射流激励位置的变化

Sjet/c=0.4作为最优控制点之一的翼型流场及控制点位于Sjet/c=0.12时翼型流场如图8所示。在未施加控制时,原始流场分离从吸力面前缘开始,分离区域很大;在Sjet/c=0.12,即在分离点附近施加合成射流控制之后,分离区的面积明显减小;在分离区内部Sjet/c=0.4处施加控制后,分离区减小更加明显。三者气动性能的定量对比如表1所示。当合成射流布置在分离点附近时,翼型性能相对控制前大幅提升,升阻比增加了126.2%,分离点由x/c=0.132推迟到x/c=0.313。但是,当合成射流布置在Sjet/c=0.4处,分离控制的效果相比控制点在分离点附近时更好,升阻比相比控制前提升293%,分离点推迟到x/c=0.591。

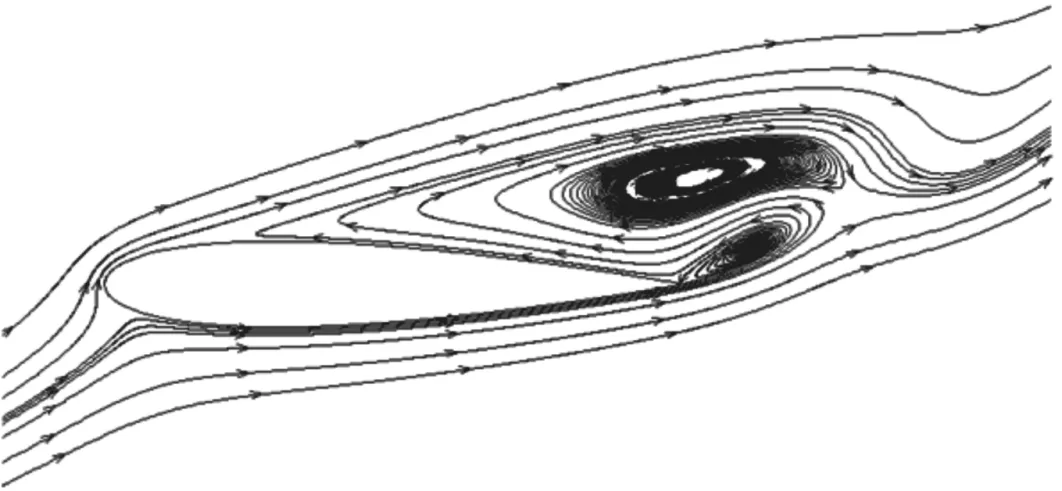
(a)无控制

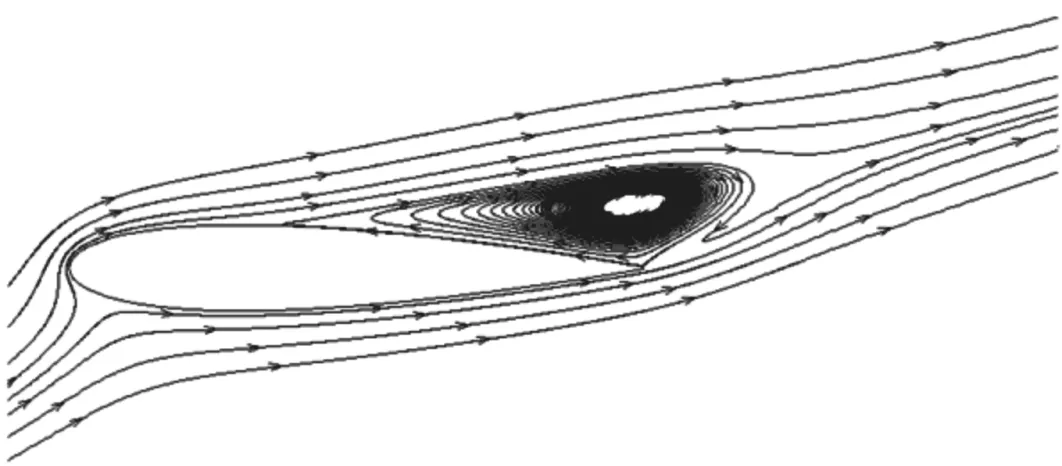
(b)Sjet/c=0.12

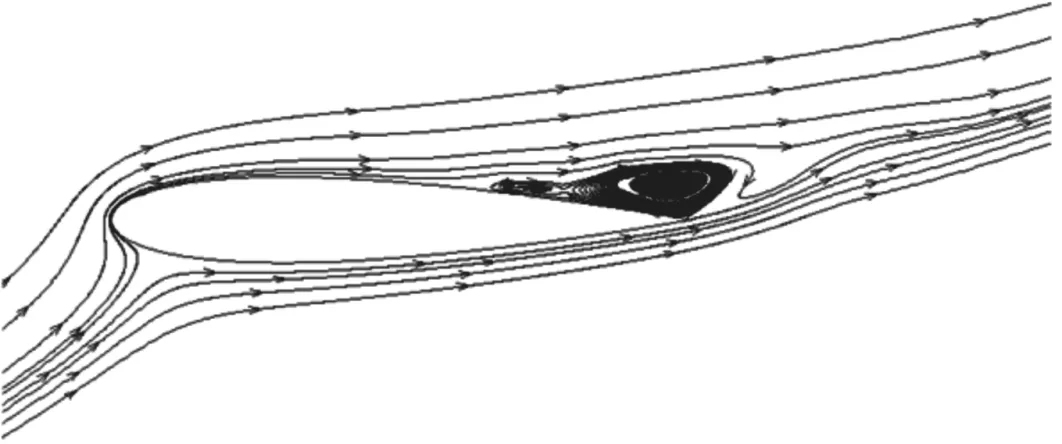
(c)Sjet/c=0.40图8 翼型附近的时均流线图

控制点位于Sjet/c=0.12、Sjet/c=0.4时翼型表面时均压力系数分布如图9所示。可以看出,合成射流控制对翼型绕流的影响是全局性的。相对控制前,Sjet/c=0.12时翼型吸力面的压力系数峰值的绝对值大幅增加,该值平台区缩短,压力面绝大部分区域的压力系数也有所增加。翼型前缘下游处尖锋突起对应着合成射流的作用位置。Sjet/c=0.4时吸力面压力系数峰值的绝对值继续增加,在控制点之前的压力系数小于控制前,在控制点之后的压力系数大于控制前,在压力面的压力系数大于Sjet/c=0.12时的压力系数。压力系数分布的不同也导致了这2种控制的升力系数出现差异。

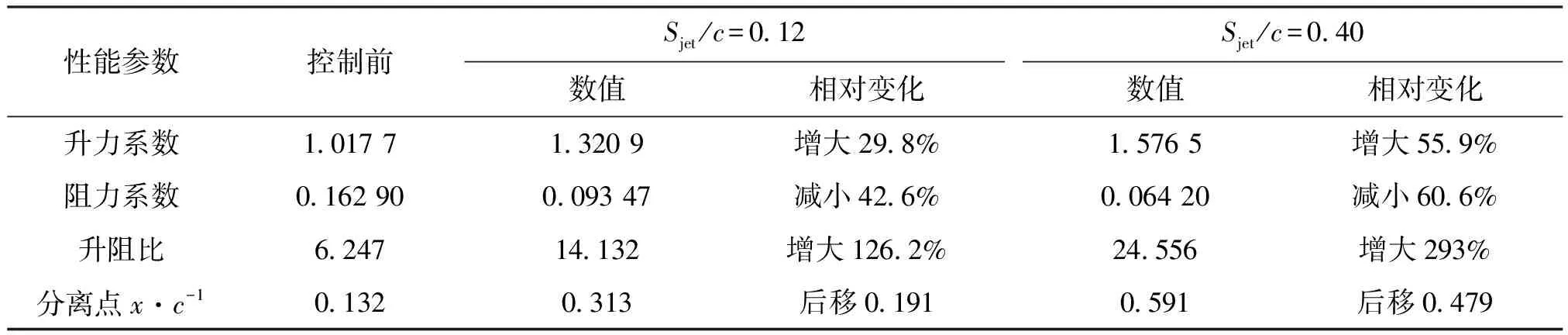
表1 控制前、Sjet/c=0.12和Sjet/c=0.40时的气动性能对比

综合来看,在大攻角下,翼型原始流场分离点位于靠近前缘的位置,在分离点附近至分离点中部一定位置均可以有效控制分离,提升翼型的气动性能,其中位于分离区内部Sjet/c=0.3～0.4的控制效果最优。虽然已有研究表明尾缘控制对于小攻角情况有一定的作用[9],但对大攻角情况并非如此。

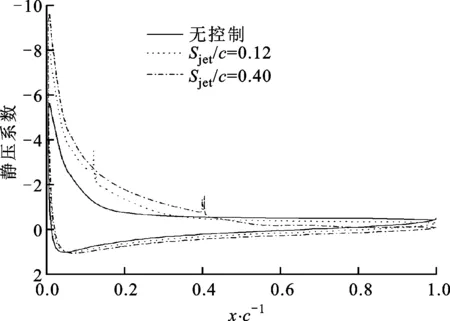
图9 时均压力系数分布对比

3 基于POD的流场分析

3.1 POD原理

POD由Lumley提出[19],是一种针对非定常流场实验或者计算结果的一种流场分析方法,其通过对非定常流场的时空解耦,提取出湍流大尺度结构。在Lumley方法的基础上,Sirovich提出了目前广泛使用的POD snapshots(快照)方法[20]。

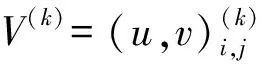
(2)

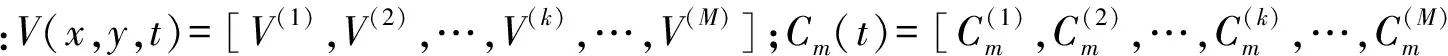
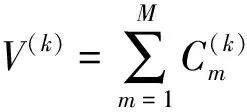
(3)

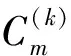
3.2 控制前流场的POD分析

在大于3倍流场周期的时间范围内,等时间间距取150个瞬时速度场快照作为基本数据,分别对无控流场和在不同点处施加合成射流的流场进行POD分析。

无控流场的POD分析提取出的前五阶模态所占能量比例如表2所示。前五阶模态已经包含了几乎全部的模态能量,更高阶模态对应的能量趋于0。一阶模态在翼型附近的流线如图10a所示,该形态与图8a中时均流线非常相近,代表非定常流动的平均流动成分,占据了整个非定常流场的绝大部分能量。二阶模态和更高阶模态对应流场中相应能量的湍流大尺度结构分布,它们所占能量的相对比例较小且呈递减变化。二阶模态的流线如图10b所示,其中翼型上表面附近和翼型后部尾迹区内的涡系代表了相应位置的湍流大尺度结构。

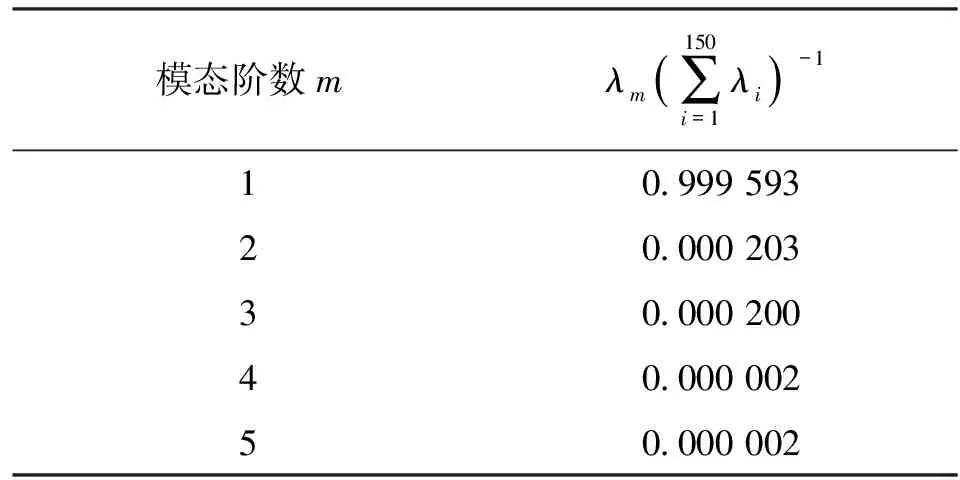
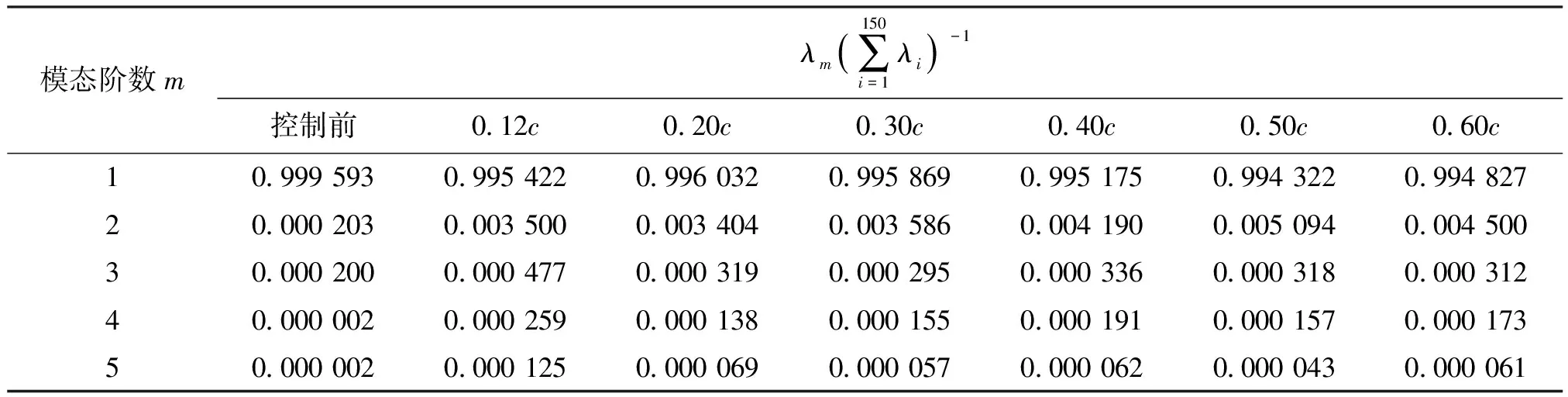
表2 无控制时的流场前五阶模态及其能量比例

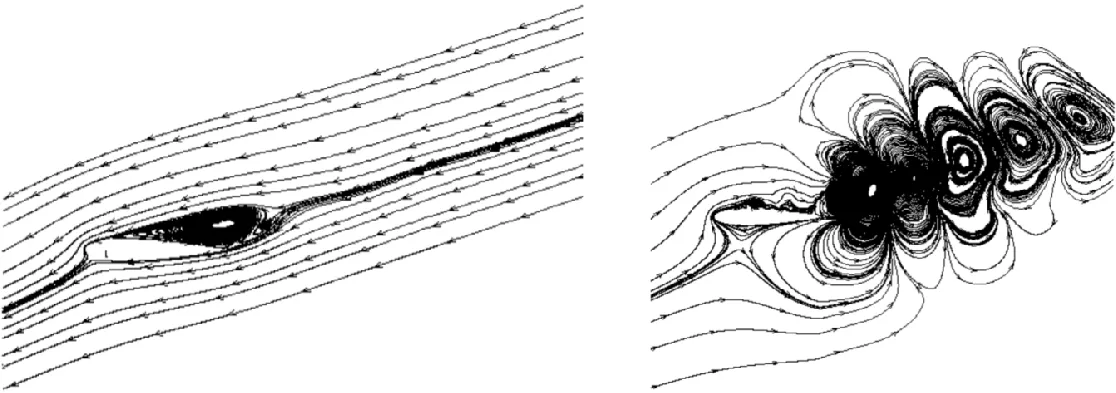
(a)一阶模态 (b)二阶模态图10 无控制时速度场一阶和二阶模态

3.3 无控流场和控制后流场的对比分析

从计算中选取有代表性的Sjet/c=0.12～0.60之间的位置,将其POD分析结果与无控流场进行了比较。Sjet/c=0.12～0.4为有效控制区,Sjet/c为0.3和0.4的控制效果最好,Sjet/c为0.5和0.6时为无效控制。

3.3.1 模态时间系数的对比 模态时间系数反映了各模态的时间特性。一阶和二阶模态时间系数随时间的变化如图11所示。可以看出,合成射流的引入明显增强了流场各阶模态的非定常波动幅度。当Sjet/c=0.12时,一阶模态的波动幅度最大,这是因为合成射流激励施加在分离点附近时,流场的不稳定性更显著。相对位于Sjet/c=0.5～0.6的无效控制,在Sjet/c=0.12～0.4的有效控制后一阶模态波动的均值显著下降。

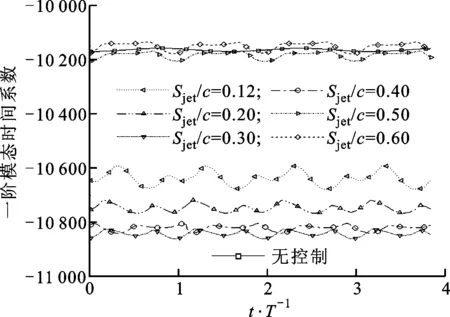
(a)一阶模态

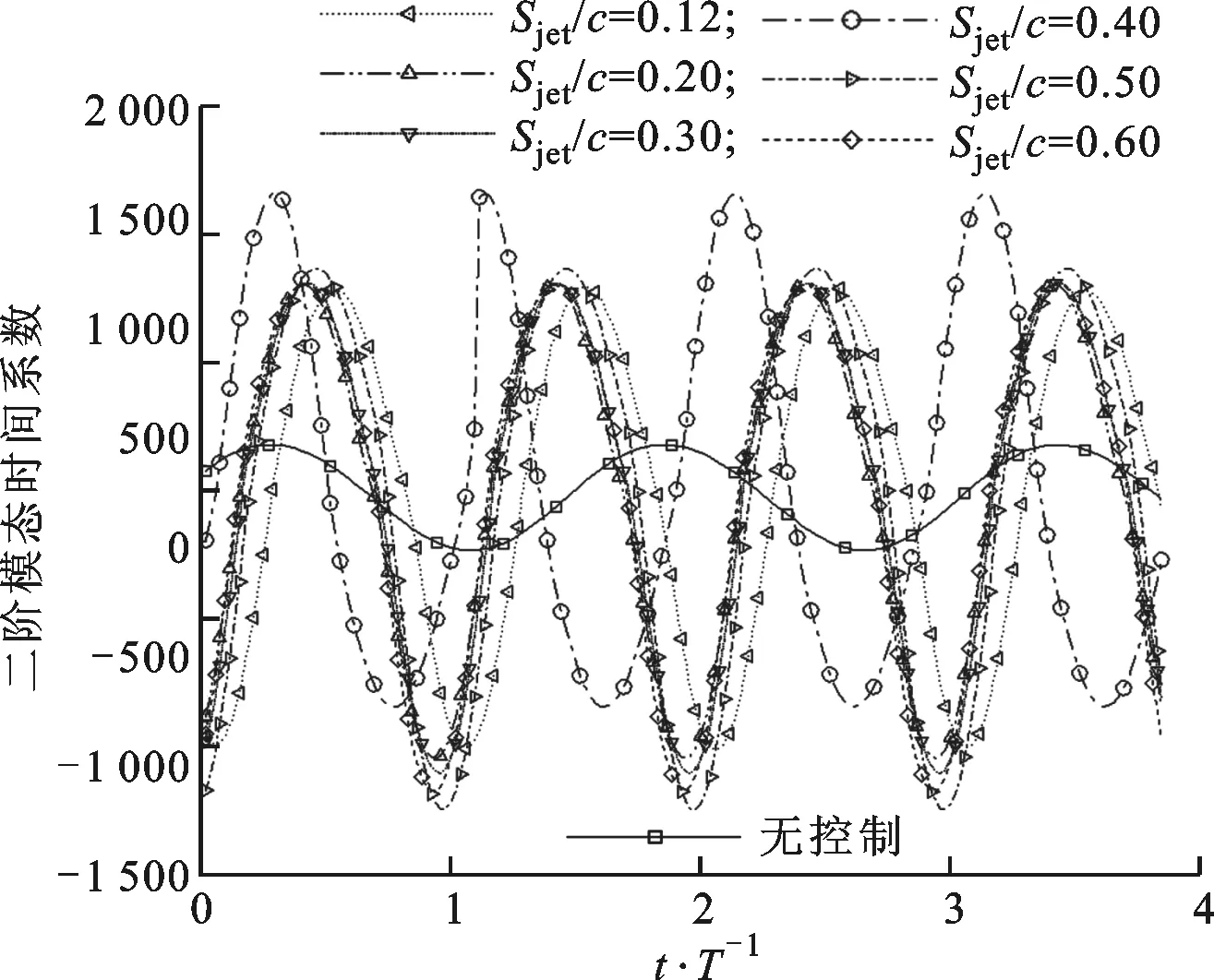
(b)二阶模态T:合成射流周期图11 无控流场及一阶和二阶模态时间系数随时间的变化

3.3.2 各阶模态能量分配的对比 合成射流控制后流场各阶模态能量分配与控制前的对比如图12和表3所示。施加合成射流后二阶以上模态能量比例大幅提升,一阶模态所占能量比例下降。可见,合成射流的引入使能量在各阶模态间的分配发生了变化,能量从代表平均流的一阶模态转移到代表流场内大尺度拟序结构的二阶以上模态。四阶以上模态能量比例极小,二、三阶模态是代表大尺度拟序结构的主要模态。控制前二阶模态所占能量比例与三阶模态近似,控制后二阶模态所占能量比例提升了一个数量级,其相对三阶模态对合成射流激励的响应程度更大。

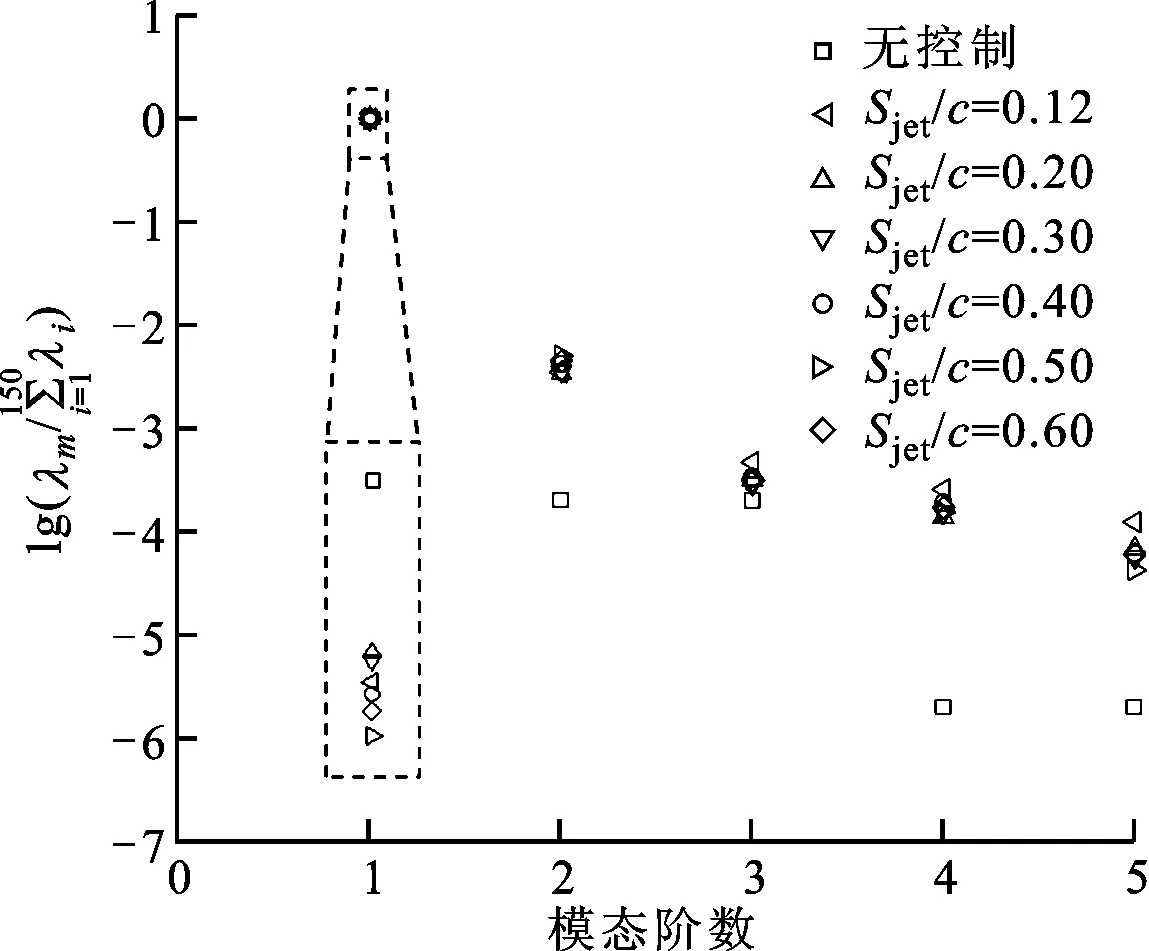
图12 各阶模态所占比例对比

3.3.3 主要模态的形态分析 一阶模态代表平均流动,而分离点是一阶模态在翼型上表面的流场特征位置。从计算结果已知,代表平均流的时均分离点并非合成射流激励的最优位置,合成射流的最优作用位置应由代表流场中大尺度湍流结构的二阶及以上模态的特征位置决定,见图12。在这些模态中,二、三阶模态占据了绝大部分的能量,其中二阶模态对合成射流激励有相对最强的响应。合成射流激励的最佳位置应与二阶模态的特征位置有关。

无控制时翼型附近流场二阶模态的流线如图13所示。可以看出,该翼型表面存在一个显著的涡团。该涡结构所在的位置为x/c=0.282～0.443,效果最好的控制点位于该范围之内。

图13 无控时流场二阶模态流线图

合成射流位置Sjet/c=0.12～0.6时控制后流场的二阶模态流线如图14所示。前文中提到控制效果从Sjet/c=0.4到Sjet/c=0.5骤然下降,相应地控制后流场二阶模态结构也明显不同。Sjet/c=0.12～0.4(对应有效控制区)时,从合成射流激励位置到尾缘之间有一系列连续分布的涡团,合成射流与边界层相互作用的影响向下游传递,并对翼型流场产生了全局性影响。Sjet/c=0.5～0.6(对应无效控制区)时,控制后的翼型表面仅在合成射流激励位置附近有一个涡结构,其与尾缘之间并未出现与Sjet/c=0.4类似的连续分布的涡,这反映了合成射流对翼型上表面分离区的影响局限在射流激励位置附近,无法对整个分离流动产生显著影响。

以上的现象可以由控制前流场二阶模态位于翼型上表面x/c=0.282～0.443之间的特征涡结构(见图13)来解释,该涡结构所在位置为分离区的特征位置。当合成射流布置在Sjet/c=0.12～0.4之间时,控制点位于该特征涡团位置或者距涡团较近的上游,合成射流激励可以在下游影响该特征涡团,从而对分离区产生显著影响,达到好的控制效果。当激励位置在Sjet/c=0.3和0.4时,控制点恰好位于特征涡团范围内,可对分离区产生更大的影响,于是这2个位置的激励表现出了优于其他位置的控制效果。当控制点位于Sjet/c=0.5及下游时,射流无法影响到位于上游的特征涡团结构,亦无法有效控制分离,故升阻比逐渐减小。但是,合成射流激励改变了模态结构,使得最终二阶模态流线图中只出现了在激励位置附近的涡结构。此外,Sjet/c=0.05虽然位于该特征涡团的上游,但是因为距离较远,无法产生足够的影响,故靠近前缘的Sjet/c=0.05处无控制效果。

综上所述,在大攻角下,合成射流控制的最佳位置并不是代表平均流动的一阶模态的特征位置时均分离点,而与代表湍流大尺度结构的二阶模态的特征涡团所在位置有关,在该位置及距其较近的上游区域可以获得较好的控制效果,在该位置可以获得相对最好的控制效果,在该位置下游则几乎无效果。

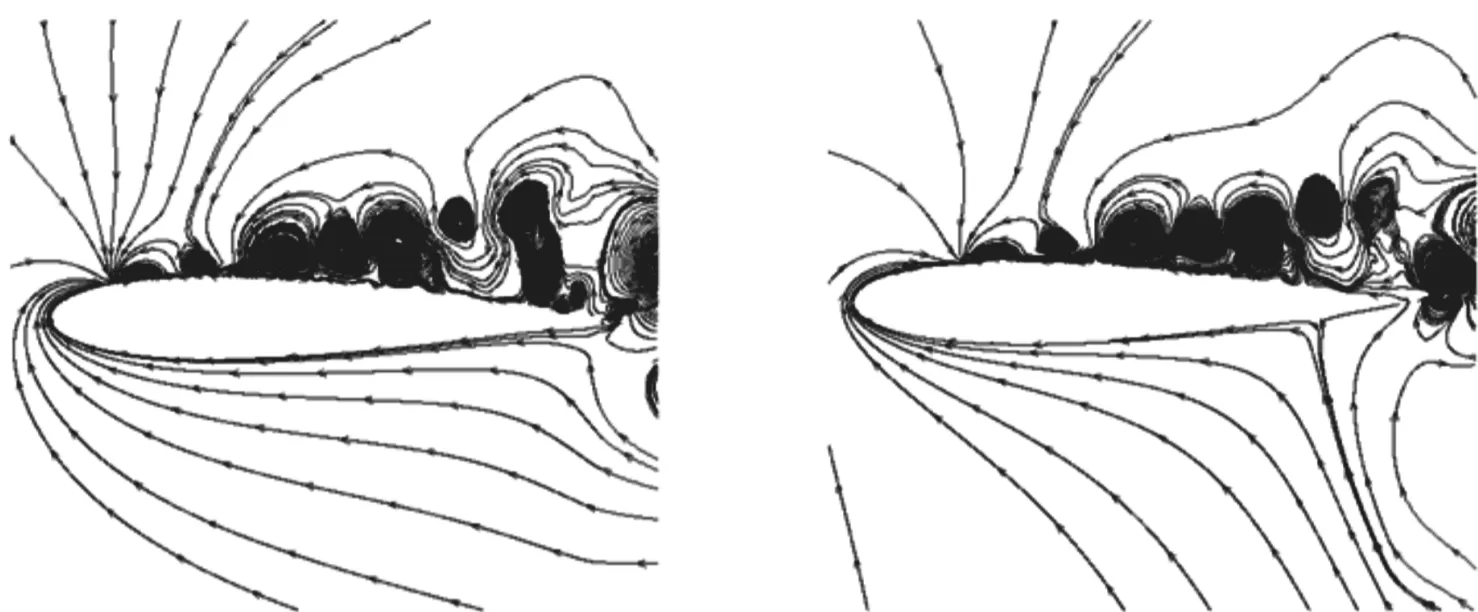
(a)Sjet/c=0.12 (b)Sjet/c=0.20

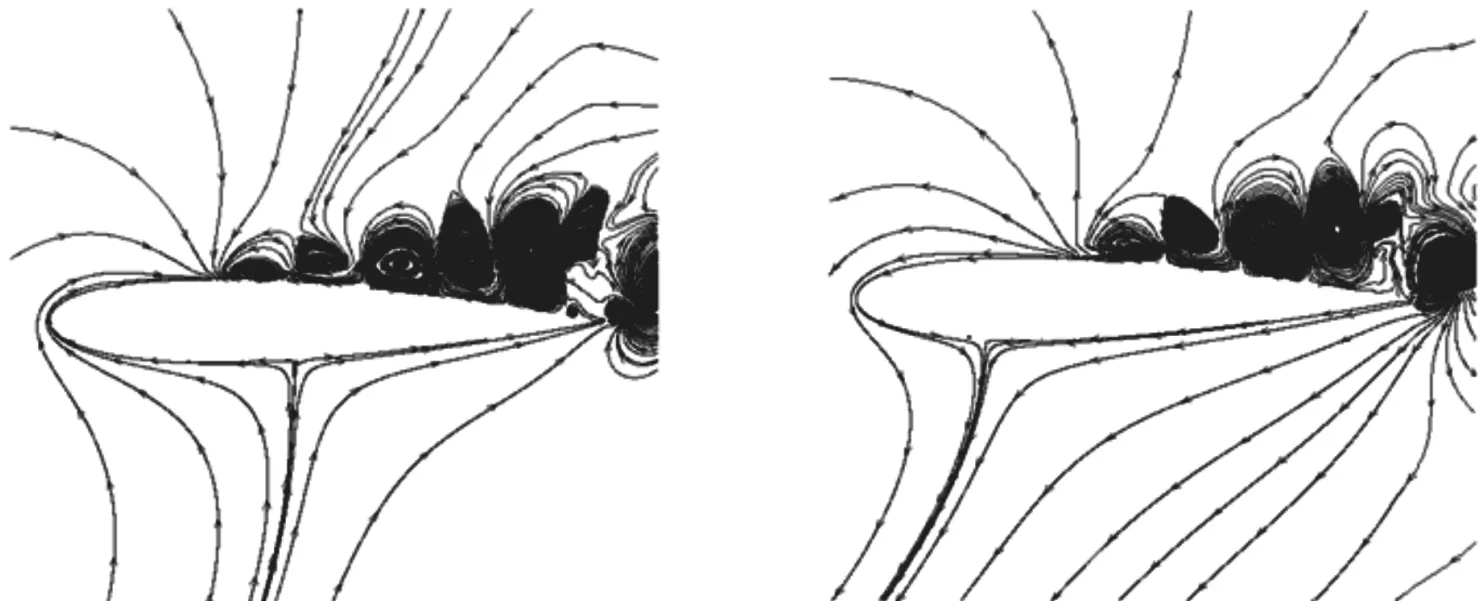
(c)Sjet/c=0.30 (d)Sjet/c=0.40

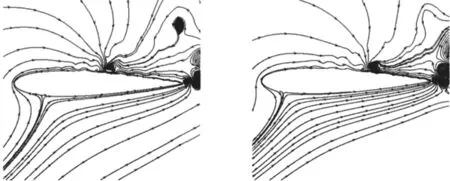
(e)Sjet/c=0.50 (f)Sjet/c=0.60图14 控制后流场的二阶模态流线图

4 结 论

本文以NACA0015翼型为研究对象,研究了大攻角(α=20°)下合成射流激励位置对分离流动控制效果的影响,并通过POD方法对计算结果进行了分析和解释。

研究表明,当攻角为20°时,翼型表面流动分离严重,单个合成射流激励的控制效果随位置的不同而变化,合成射流的最优控制位置并不是分离点,而是位于分离区内部Sjet/c=0.3～0.4范围。当合成射流激励位于Sjet/c=0.12～0.4时,分离得到有效控制,分离点大大后移,增升减阻的效果显著。Sjet/c=0.3～0.4时控制效果相对最好,较控制前的升阻比提升了293%。Sjet/c=0.05或Sjet/c=0.5～0.95时,合成射流控制几乎无效果。

通过POD分析表明,合成射流控制增加了流场的非定常波动幅度,改变了流场各主要模态之间的能量分配,使得一阶模态所占能量减少,二阶及以上模态所占能量增加。合成射流的最佳控制位置与一阶模态的特征位置分离点不对应,而与二阶模态中翼型上表面的特征涡结构有关,它代表了二阶模态的特征位置。有效的控制必须位于二阶模态中的特征涡区域或者距离涡较近的上游位置。

[1] VAN DEN BERG B, OSKAM B. Boundary layer measurements on a two-dimensional wing with flap and a comparison with calculations [R]. Amsterdam, Netherlands: National Aerospace Lab. , 1980.

[2] JIRASEK A. A modified vortex generator model and its application to complex aerodynamic flows [R/OL]. [2015-12-25]. http: ∥www. foi. se/RepovtFiles/foir_1204. pdf.

[3] GLEZER A, AMITAY M. Synthetic jets [J]. Annual Review of Fluid Mechanics, 2002, 34(1): 503-529.

[4] 张攀峰, 王晋军, 冯立好. 零质量射流技术及其应用研究进展 [J]. 中国科学: E 辑, 2008, 38(3): 321-349. ZHANG Panfeng, WANG Jinjun, FENG Lihao. Zero-net-mass-flux jet techniques and its research progress [J]. Science in China: E, 2008, 38(3): 321-349.

[5] 李斌斌. 合成射流及在主动流动控制中的应用 [D]. 南京: 南京航空航天大学, 2012.

[6] WILTSE J M, GLEZER A. Manipulation of free shear flows using piezoelectric actuators [J]. Journal of Fluid Mechanics, 1993, 249: 261-285.

[7] ZEIGERM M. Distributed hingeless flow control and rotary synthetic jet actuation [C]∥42nd AIAA Aerospace Sciences Meeting and Exhibit. Reno, NV, USA: AIAA, 2004: 224.

[8] WHITEHEAD J, GURSUL I. Interaction of synthetic jet propulsion with airfoil aerodynamics at low Reynolds numbers [J]. AIAA Journal, 2006, 44(8): 1753-1766.

[9] 刘小波, 张伟伟, 蒋跃文, 等. 尾缘合成射流影响翼型非定常气动特性的数值研究 [J]. 空气动力学学报, 2012, 30(5): 606-612. LIU Xiaobo, ZHANG Weiwei, JIANG Yuewen, et al. Numerical study on unsteady aerodynamic characteristics of an airfoil with a synthetic jet set in trailing edge [J]. Acta Aerodynamica Sinica, 2012, 30(5): 606-612.

[10]SEIFERT A, DARABI A, WYGANSKI I. Delay of airfoil stall by periodic excitation [J]. Journal of Aircraft, 1996, 33(4): 691-698.

[11]HE Y, CARY A W, PETERS D A. Parametric and dynamic modeling for synthetic jet control of a post-stall airfoil [C]∥39th Aerospace Sciences Meeting and Exhibit. Reno, NV, USA: AIAA, 2001: 733.

[12]RAJU R, MITTAL R, CATTAFESTA L N. Towards physics based strategies for separation control over an airfoil using synthetic jets[R]. Reno, NV, USA: AIAA, 2007: 1421.

[13]李玉杰, 罗振兵, 邓雄, 等. 合成双射流控制NACA0015翼型大攻角流动分离试验研究 [J]. 航空学报, 2016, 37(3): 817-825. LI Yujie, LUO Zhenbing, DENG Xiong, et al. Experimental investigation on flow separation control of stalled NACA0015 airfoil using dual synthetic jet actuator [J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 817-825.

[14]CHAPIN V G, BENARD E. Active control of a stalled airfoil through steady or unsteady actuation jets [J]. Journal of Fluid Engineering, 2015, 37: 091103.

[15]DURAISAMY K, BAEDER J D. Active flow control concepts for rotor airfoils using synthetic jets [C]∥1st Flow Control Conference. Reno, NV, USA: AIAA, 2002: 2835.

[16]REHMAN A, KONTIS K. Synthetic jet control effectiveness on stationary and pitching airfoils [J]. Journal of Aircraft, 2006, 43(6): 1782-1789.

[17]GILARRANZ J L, TRAUB L W, REDINIOTIS O K. A new class of synthetic jet actuators: part II Application to flow separation control [J]. Journal of Fluids Engineering, 2005, 127(2): 377-387.

[18]DONOVAN J F, KRAL L D, CARY A W. Active flow control applied to an airfoil [C]∥36th AIAA Aerospace Sciences Meeting and Exhibit. Reno, NV, USA: AIAA, 1998: 210.

[19]LUMLEY J L. Stochastic tools in turbulence [M/OL]. [2016-01-10]. http:∥www.overdrive.com/1749883/stochastic-tools-in-turbulence.

[20]SIROVICH L. Turbulence and the dynamics of coherent structures: part I Coherent structures [J]. Quarterly of Applied Mathematics, 1987, 45(3): 561-571.

[21]CHEN H, REUSS D L, HUNG D L S, et al. A practical guide for using proper orthogonal decomposition in engine research [J]. International Journal of Engine Research, 2013, 14(4): 307-319.

(编辑 苗凌)

Numerical Investigation for Influence of Synthetic Jet Actuation Location on Airfoil Flow Separation Control at Large Attack Angle

LAN Aiqing,WANG Zhiheng,YU Hongshi,XI Guang

(School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

For a NACA0015 airfoil, 2-D unsteady flow fields are calculated when a synthetic jet is put at different locations on the suction surface at a large attack angle (α=20°) and Reynolds number of 8.96×105based on chord length. POD (proper orthogonal decomposition) method is utilized to analyze the computation results, and relevant control mechanisms are explained. The results show that actuation location of a synthetic jet exerts significant influence on effects of flow separation control. When the actuator is located between 0.12 and 0.40 of chord length, flow separation on the airfoil is effectively suppressed, enhancing lift coefficient and reducing drag coefficient with lift to drag ratio increasing by 293%. The optimal location is not near the time-averaged separation point as widely suggested but at some downstream locations inside the separation zone. POD analysis on computation results indicates that the introduction of synthetic jets would change the energy distribution among different modes, and that energy is transferred from 1st-order mode representing mean flow to 2nd-order mode or higher modes which represent large scale coherent structures. The best location for synthetic jet actuation is closely related to the site of a characteristic vortex on the suction side of the airfoil in 2nd-order mode. In order to reach optimal control effects, synthetic actuation should be located within the covering range of the characteristic vortex. It is ineffective to put a synthetic jet at downstream or far upstream of the location of that vortex.

synthetic jet; airfoil flow separation; actuation location; proper orthogonal decomposition

2016-02-04。 作者简介:兰艾青(1990—),男,硕士生;席光(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51236006,51576153)。

时间:2016-05-10

10.7652/xjtuxb201607017

V211.3

A

0253-987X(2016)07-0110-08

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160510.1517.004.html