小猫能否晒到太阳
小猫能否晒到太阳
周玉俊
数学源于生活,生活中处处有数学.本文通过一道中考试题的解析与变式,探究锐角三角函数解决实际问题的思路与策略,以帮助同学们找寻和感悟通过建立数学模型解决此类问题的一般思路与方法.
中考在线:(2015·江苏盐城)如图1所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α.当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.
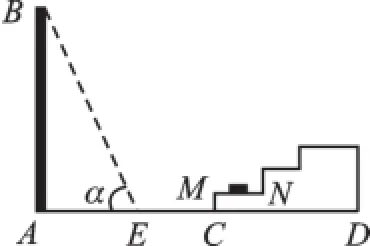
图1
责任编辑:彭深
email:2020748334@qq.com
(1)求楼房的高度约为多少米?(3取1.73)
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.
【分析】(1)在Rt△ABE中,α=60°,AE= 10(米),由tan60°=,即可求出AB的长度.
(2)如果把小猫看成是线段MN上的一点,小猫能否晒到太阳,关键是看从点B射下的光线能否经过线段MN上的这一点,为此,需要我们构造恰当的直角三角形,通过具体的计算来解决问题.
【解答】(1)当α=60°时,在Rt△ABE中,
(2)当α=45°时,小猫仍可以晒到太阳.
理由如下:
解题策略一:以A为直角顶点,AB为一边,构造含45°角的直角三角形.
方法1:假设没有台阶,当α=45°时,如图2,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.
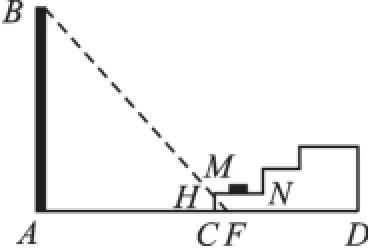
图2
此时的影长AF=AB=17.3(米),
∴CF=AF-AC=17.3-17.2=0.1(米),
∴CH=CF=0.1(米)<0.2(米),
∴大楼的影子落在台阶MC这个侧面上,
∴小猫仍可以晒到太阳.
方法2:如图2,在AD上取点F,使AF= AB=17.3(米),连接BF.
易知∠BFA=45°,CF=AF-AC=0.1(米),设BF与直线CM交于H点,在Rt△HCF中,CH= CF=0.1(米),
∵台阶每层高0.2米,
∴大楼的影子落在台阶MC这个侧面上,
∴小猫仍可以晒到太阳.
解题策略二:过M作MG⊥AB于G点(如图3),

图3
构造以G为直角顶点,GB为一边且含45°角的直角三角形.
方法3:如图4,当α=45°时,从点B射下的光线与MG的交点为点P,在Rt△BGP中,可求GP=GB=17.1(米),从而MP=MG-GP=0.1(米),
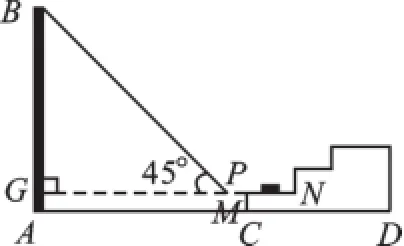
图4
∴大楼的影子会落在台阶MC这个侧面上.
∴小猫仍可以晒到太阳.
方法4:类似于方法2,如图4,在GM上取点P,使PG=BG=17.3-0.2=17.1(米),连接BP,得等腰Rt△BGP,以下同方法3.
解题策略三:在直线MC上寻找α=45°时太阳光线照射的位置
方法5:如图5,设从点B射下的光线与MC所在直线交于点F,过F点作FG⊥AB于点G,
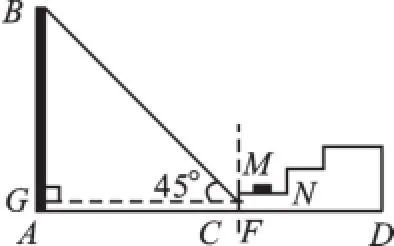
图5
在Rt△BGF中可求得BG=GF=17.2(米),
∴FC=GA=BA-BG=17.3-17.2=0.1(米),
∴FC<MC,
∴大楼的影子还没有到达点M,
∴小猫仍可以晒到太阳.
方法6:如图6,连接BM并延长交AD于 Q,由△CMQ∽△ABQ得:,即,所以CQ≈0.2,AQ=17.4,从而得tan∠AQB<1,所以∠AQB<45°,故当α=45°时,从点B射下的光线必然落在台阶MC这个侧面上.
∴小猫仍可以晒到太阳.

图6
点评:本题虽是一道生活中的实际问题,但从数学的角度看,第(1)小题实质上是在直角三角形中,已知一条直角边和一个锐角,求另一条直角边,用正切列出关系式即可求解;对于第(2)小题小猫能否晒到太阳,实质是看从点B射下的光线(即射线BM)能否经过线段MN上的点,为此,需要我们构造恰当的直角三角形,通过计算线段的长度来解决问题.
变式探究:
变式1:改变每层台阶的高度.假定每层台阶的高度为0.08米,原题其余条件不变,问小猫还能否晒到太阳?
变式2:改变AC的长度.将AC的长改为16.5米,并假定每层台阶的宽为0.5米(即MN= 0.5米),原题其余条件不变,问小猫还能否晒到太阳?
变式3:改变角α的度数.若AC=17.1米,α<45°,原题其余条件不变,问小猫还能否晒到太阳?
变式4:改变小猫所在的位置.若小猫睡在台阶的第二层,假定每层台阶的宽为0.5米,且AC=16.5米,原题其余条件不变,问小猫还能否晒到太阳?
说明:以上各题虽然条件各不相同,但解决问题的方法在本质上是一致的,即构造恰当的直角三角形,再运用三角函数关系计算出有关的边和角,最后通过比较线段的长度或角的大小来求解.(结果由同学们自己探究)
由此可见,只要我们在日常的学习和生活中善于用数学的眼光去观察世界,并能从中发现问题、思考问题和解决问题,不断增强运用数学知识解决实际问题的意识和能力,我们就一定会越学越聪明,越学越快乐!
(作者单位:江苏省东台市教育局教研室)

